【算法】刷题中的位运算
作者:指针不指南吗
专栏:算法篇🐾人类做题的过程,其实是暴搜的过程🐾
文章目录
- 1.位运算概述
- 2.位运算符
- 3.位运算应用
- 3.1整数的奇偶性判断
- 3.2有关 2 的幂的应用
- 3.3lowbit(x)返回x的最后一位1
- 3.4二进制数中1的个数
- 3.5求二进制位的某一位是几
- 3.6交换两个整型变量的值
- 3.7数组中x出现的次数
- 3.8快速幂取模
- 4.位运算总结
简单介绍一下位运算概念,更多的是写位运算在刷题过程中的应用
1.位运算概述
位运算就是直接对整数在内存中的二进制位进行操作,由于计算机内部就是以二进制来存储数据,位运算是相当快的。
基本的位运算共 6种,分别为按位与、按位或、按位异或、按位取反、左移和右移。
位运算一般有三种作用:
- 高效地进行某些运算,代替其它低效的方式。
- 表示集合。(常用于状压DP )
- 题目本来就要求进行位运算。
2.位运算符
| 含义 | 符号 | 简述 |
|---|---|---|
| 按位与 | a & b | 同一得 1 |
| 按位或 | a | b | 有一得 1 |
| 按位异或 | a ^ b | 相同得 0 |
| 按位取反 | ~a | 取反 |
| 左移 | a << b | 向左移动,低位补零,高位舍弃 |
| 带符号右移 | a >> b | 向右移动,高位补原有高位,低位舍弃 |
-
复合赋值位运算符
和
+=,-=等运算符类似,位运算也有复合赋值运算符:&=,|=,^=,<<=,>>=。(取反是单目运算,所以没有) -
数组初始化
memset(f,0x3f,sizeof(f)) -
位移运算符
左移运算符 << 二进制 : 1 -> 10 -> 100 -> 1000 十进制 : 1 -> 2 -> 4 -> 8 综上所述:1 << n == 2^n 右移运算符 >> 二进制 : 1000 -> 100 -> 10 -> 1 十进制 : 8 -> 4 -> 2 -> 1 综上所述: n >> x == n / (2^x) -
运算符优先级
~的优先级最高,其次是<<、>>,再次是&,然后是^,优先级最低的是|。
位运算的优先级 低于 算术运算符(除了取反),而按位与、按位或及异或 低于 比较运算符(详见 运算页面 ),所以使用时需多加注意,在必要时添加括号。
3.位运算应用
3.1整数的奇偶性判断
-
朴素做法
if(a%2==1)//为奇数 else//为偶数 -
按位与 -> 二进制的末位为0表示偶数,最末位为1表示奇数
if(a & 1 != 1)//为奇数 else//为偶数
3.2有关 2 的幂的应用
将一个数乘(除) 2 的非负整数次幂
// 计算 n*(2^m)
int mulPowerOfTwo(int n, int m)
{return n << m;
}// 计算 n/(2^m)
int divPowerOfTwo(int n, int m)
{return n >> m;
}
判断一个数是否是2的幂次方,若是,并判断出来是多少次方
题目链接: 力扣 231. 2的幂
将2的幂次方写成二进制形式后,很容易就会发现有一个特点:二进制中只有一个1,并且1后面跟了n个0; 因此问题可以转化为判断1后面是否跟了n个0就可以了
如果将这个数减去1后会发现,仅有的那个1会变为0,而原来的那n个0会变为1;因此将原来的数与去减去1后的数字进行与运算后会发现为零。
最快速的方法:(number & number - 1) == 0原因:因为2的N次方换算是二进制为10……0这样的形式(0除外)。按位与上自己-1的位数,这们得到结果为0。例如,8的二进制为1000;8-1=7,7的二进制为111。两者相与的结果为0。计算如下:1000& 0111-------0000
代码实现如下:
#include<bits/stdc++.h>
using namespace std;//判断一个数是2的多少次方
int log2(int value)
{int x=0;while(value>1){value>>=1;x++;}return x;
}int main()
{int num;scanf("%d",&num);//使用与运算判断一个数是否是2的幂次方if(num&(num-1)) printf("%d不是2的幂次方!\n",num);elseprintf("%d是2的%d次方!\n",num,log2(num));return 0;
}
3.3lowbit(x)返回x的最后一位1
lowbit(x):返回x的最后一位1,即一个二进制最低位的1与后边的0组成的数。
x = 1010 lowbit(x) = 10
x= 101000 lowbit(x) = 1000
实现原理:x & -x = x & (~x + 1),负数的补码:原码取反加一(利用了负整数的补码特性)
3.4二进制数中1的个数
题目链接:力扣 191.位1的个数
-
朴素做法 -> 使用移位操作,判末位是否为1;移位的次数为32
int BitCount(unsigned int n) {unsigned int c =0 ; // 计数器while (n >0){if((n &1) ==1) // 当前位是1++c ; // 计数器加1n >>=1 ; // 移位}return c ; } -
快速做法 -> 迭代n=n&(n-1),消除最右边的1,计数
int BitCount2(unsigned int n) {unsigned int c =0 ;for (c =0; n; ++c){n &= (n -1) ; // 清除最低位的1}return c ; }
3.5求二进制位的某一位是几
n 的二进制中第 k 位数字
先把第k为移到最后一位
n>>k看个位是几
x&1把上面两步综合 即
n>>k&1
应用:输出n=10的二进制
#include<bits/stdc++.h>
using namespace std;int main()
{int n=10;for(int k=3;k>=0;k--) //从0位开始的(右到左)cout<<(n>>k&1);return 0;
}
3.6交换两个整型变量的值
异或的性质:
1.交换律:可任意交换运算因子的位置,结果不变;
如:a ^ b ^ c = b ^ a ^ c;
2.结合律:即(a ^ b) ^ c == a ^ ( b ^ c) ;
3.对于任何数x, 都有x ^ x = 0, x ^ 0 = x,同自己求异或为0,同0求异或为自己
4.自反性:A ^ B ^ B = A ^ 0 = A, 连续和同一个因子做异或运算,最终结果为自己
例题:int A = 10, int B = 20, 在不引入第3个变量的情况下,交换两个变量的值。
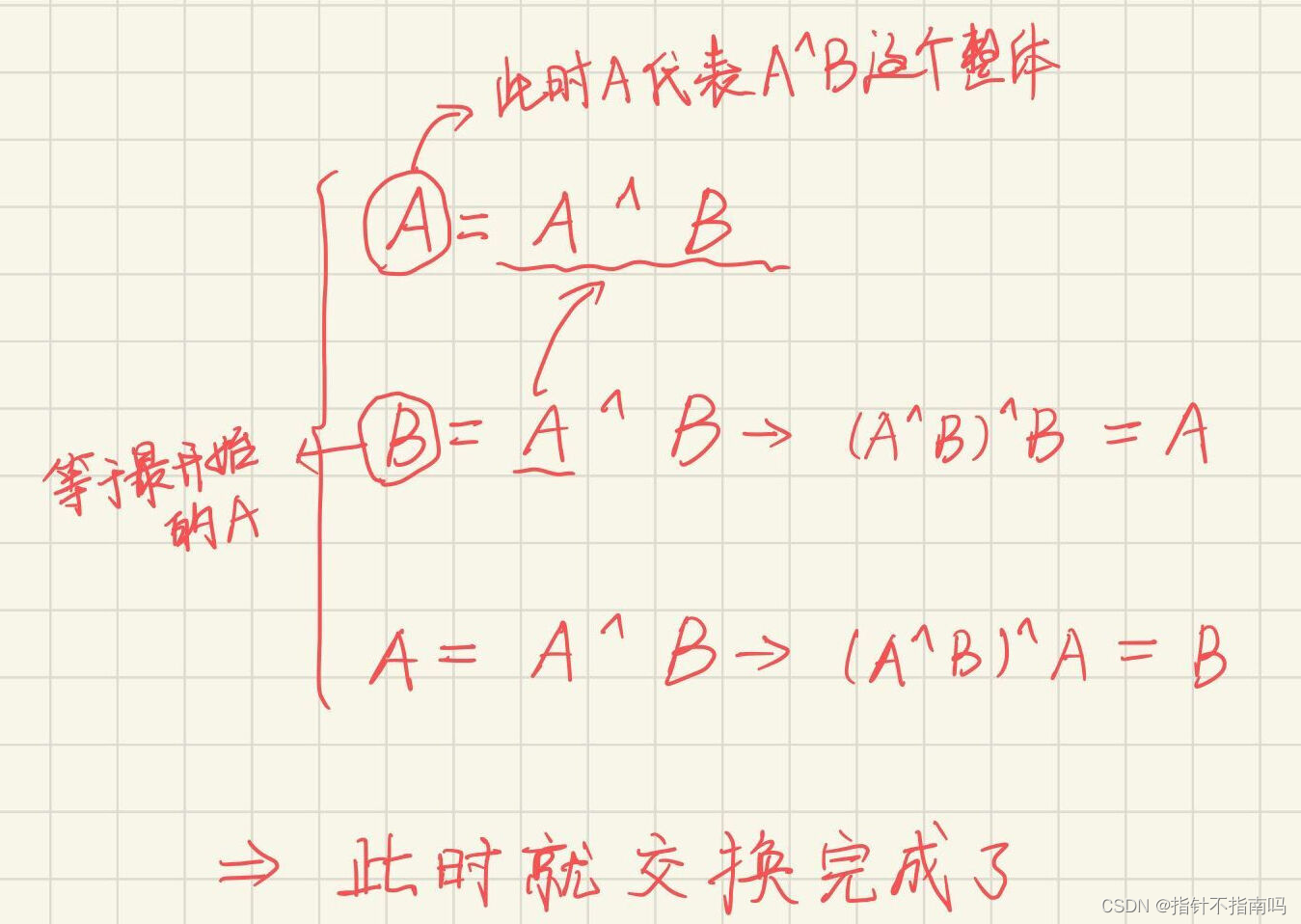
异或法——代码实现
#include<bits/stdc++.h>
using namespace std;int main()
{int A = 10;int B = 20;printf("交换前A = %d B = %d\n", A, B);A = A ^ B;B = A ^ B;A = A ^ B;printf("交换后A = %d B = %d\n", A, B);return 0;
}
3.7数组中x出现的次数
应用一:数组中,只有一个数出现一次,剩下都出现两次,找出出现一次的数
题目链接:力扣 136.只出现一次的数字 |
因为只有一个数恰好出现一个,剩下的都出现过两次,所以只要将所有的数异或起来,就可以得到唯一的那个数,因为相同的数出现的两次,异或两次等价于没有任何操作。
代码实现
int singleNumber(int nums[])
{int result = 0, n = sizeof(nums)/sizeof(nums[0]);for (int i = 0; i < n; i++){result ^= nums[i];}return result;
}
应用二:数组中,只有一个数出现一次,剩下都出现三次,找出出现一次的数
题目链接:力扣 137.只出现一次的数字||
为了方便叙述,我们称「只出现了一次的元素」为「答案」。
由于数组中的元素都在 int(即 32 位整数)范围内,因此我们可以依次计算答案的每一个二进制位是 0还是1。具体地,考虑答案的第 i 个二进制位(i 从0开始编号),他可能为0或者1。对于数组中非答案的元素,每个元素都出现了3次,3次对应第i个二进制位和的3个0或者3个1,无论哪一种情况,他的结果相加(0或者3)都是3的倍数,答案的第 i 个二进制位就是数组中所有元素的第 i 个二进制位之和除以 3 的余数。
这样一来,对于数组中的每一个元素 x,我们使用位运算 (x>>i)&1 得到 x 的第 i 个二进制位,并将它们相加再对 3 取余,得到的结果一定为 0 或 1,即为答案的第 i 个二进制位。
代码实现
int singleNumber(vector<int>& nums)
{int ans = 0;for (int i = 0; i < 32; ++i) {int total = 0;for (int num: nums) {total += ((num >> i) & 1);}if (total % 3) {ans |= (1 << i);}}return ans;
}
针对上面进行拓展,如果是数组中,只有一个数出现一次,剩下都出现 k 次 ,找出出现一次的数呢
total % k //将3改为 k ,对 k 进行取模即可
应用三:如何找数组中唯一成对的那个数
1-10这10个数放在含有11个元素的数组中,只有唯一一个元素重复,其他均只出现一次,要求每个数组元素只能够被访问一次,请设计一个算法,将它找出来 。
位运算中 异或 ^ 的特点,A^A=0 A^0=A ,也就是说,两个相同的数字进行异或结果为0,可以用来消除重复。 可惜,题目要求寻找重复的值,所以,我们对这1001个数字 加上(1 ~ 1000)这1000个数字,这样1~1000所有的数字出现了2次,可以消除,而那个重复的数字由于加了一次,变成了3次,A ^ A ^ A =A。从而得出那个重复的A。
代码实现
int findDouble(int T[])
{int res=0; //定义一个返回结果,初始值为0,因为A^0=A//先对T数组进行异或for(int i=0;i<T.length;i++){res^=T[i];}//在与1~1000异或for(int i=1;i<=1000;i++){res^=i;}return res;
}
3.8快速幂取模
给你三个整数 a,b,p,求 a b m o d p a^ b mod p abmodp。
题目链接:P1226 【模板】快速幂 | 取余运算
取平方思路
参考文章:https://oi-wiki.org/math/binary-exponentiation/
先看这个式子 a 2 b = a 2 ∗ a b a^{2b}=a^2*a^b a2b=a2∗ab ,我们发现取平方可以缩短计算次数,我们可以按照 二进制 来表示幂。那我们来看看幂和二进制之间的关系。
举个例子讲解:例如: 3 13 = 3 ( 1101 ) 2 = 3 8 ∗ 3 4 ∗ 3 1 3^{13}=3^{(1101)_2}=3^8*3^4*3^1 313=3(1101)2=38∗34∗31
是不是发现,这里面只有二进制位是1的才乘到里面,是0的跳过,所以我们只需要用10进制转2进制的方法(不断÷2的余数,直到商为0),即可得到幂数对应的二进制数。**如果某一个二进制位是1,那就将对应的数乘到结果里面,并且底数也翻倍;如果是0,则底数也翻倍。**可看下面的推导过程,这个地方有点绕,跟着过一遍就懂了。
取模定理
(a * b) % p = (a % p * b % p) % p (3)
乘积的取模等于各个因子取模相乘然后再取模;
取模的运算不会干涉乘法运算,因此我们只需要在计算的过程中取模即可 。
快速幂代码实现
long long binpow(long long a, long long b)
{long long res = 1;while (b > 0) {if (b & 1) res = res * a;a = a * a;b >>= 1;}return res;
}
快速幂取模代码实现
long long binpow(long long a, long long b, long long m)
{a %= m;long long res = 1;while (b > 0) {if (b & 1) res = res * a % m;a = a * a % m;b >>= 1;}return res;
}
4.位运算总结
在刷题中,位运算是一个非常常见的技巧和思路。它能够在一定程度上优化时间和空间复杂度,使得程序更加高效。
在一些需要对二进制进行操作的场景中,位运算能够帮助我们更好地处理问题。比本文介绍的在统计一个数的二进制中有几个1的问题、判断一个数是否是2的幂次方、交换两个整型变量的值等等。

相关文章:

【算法】刷题中的位运算
作者:指针不指南吗 专栏:算法篇 🐾人类做题的过程,其实是暴搜的过程🐾 文章目录 1.位运算概述2.位运算符3.位运算应用3.1整数的奇偶性判断3.2有关 2 的幂的应用3.3lowbit(x)返回x的最后一位13.4二进制数中1的个数3.5求…...

9.Java中异常处理机制是什么
Java的异常处理通过五个关键字来实现,分别是捕获异常:try,catchsfinally;声明异常:throws;抛出异常:throw 一:try,catch捕获异常二:finally回收资源三&#x…...

GeoTools实战指南: 叠加GeoTIFF与Shapefile图层生成截图
GeoTools实战指南: 叠加GeoTIFF与Shapefile图层生成截图 介绍 本教程将介绍如何使用GeoTools库在Java中将栅格数据(GeoTIFF)与矢量数据(Shapefile)叠加显示,并将结果保存为PNG格式的图片文件。我们将解析和分析 RasterDataRenderer 类,并了解其中的每个方法和对象。 准…...

nginx配置sh脚本远程执行一键安装
背景 本地多机重复操作某些shell指令,分步执行,很耗费时间, 需要远程一键部署,傻瓜化运维,更为通用安装。 即参考docker通用安装 sudo curl https://get.docker.com | sh - # sudo python3 -m pip install docker-co…...

Excel表格成绩排名全攻略,让你事半功倍!
在学校或公司中,我们经常需要对成绩进行排名。如果手动计算排名,不仅费时费力,而且容易出错。幸运的是,Microsoft Excel提供了一个简单而快速的方法来计算和显示排名。 在学校或公司中,成绩排名是一项重要的任务。使用…...

Docker 持久化存储 Bind mounts
Docker 持久化存储 Bind mounts Bind mounts 的 -v 与 --mount 区别启动容器基于bind mount挂载到容器中的非空目录只读 bind mountcompose 中使用 bind mount 官方文档:https://docs.docker.com/storage/bind-mounts/ Bind mounts 的 -v 与 --mount 区别 如果使用…...

LVS +Keepalived 高可用群集部署
一、LVSKeepalived 高可用群集 在这个高度信息化的 IT 时代,企业的生产系统、业务运营、销售和支持,以及日常管理等环节越来越依赖于计算机信息和服务,对高可用(HA)技术的应用需求不断提高,以便提供持续的…...

Kafka调优
生产者 参数名称描述bootstrap.serverskafka集群的地址key.deserializerkey的反序列化类,写全类名value.deserializervalue的反序列化类,写全类名buffer.memoryRecordAccumulator缓冲区总大小,默认32mbatch.size缓冲区一批数据最大值&#x…...

Debezium系列之:详细介绍Debezium2.X版本导出Sqlserver数据库Debezium JMX指标的方法
Debezium系列之:详细介绍Debezium2.X版本导出Sqlserver数据库Debezium JMX指标的方法 一、需求背景二、相关技术文章三、安装jmx_prometheus_javaagent四、Debezium2.X版本Sqlserver数据库jmx指标格式五、导出Debezium2.X版本Sqlserver数据库jmx指标方法六、Debezium2.X版本各…...
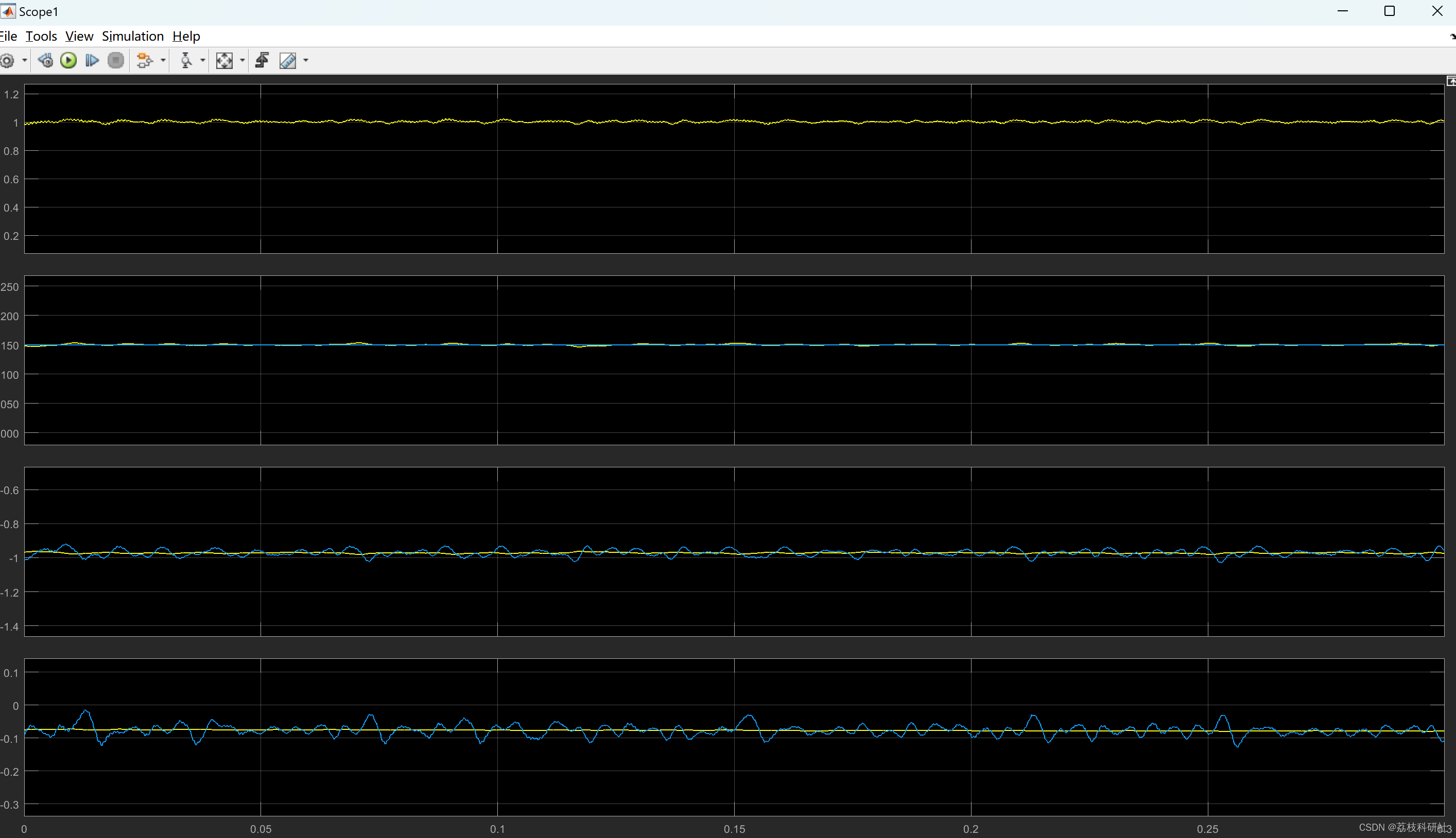
基于PWM技术的三相光伏逆变器研究(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

〖Python网络爬虫实战㉑〗- 数据存储之JSON操作
订阅:新手可以订阅我的其他专栏。免费阶段订阅量1000 python项目实战 Python编程基础教程系列(零基础小白搬砖逆袭) 说明:本专栏持续更新中,目前专栏免费订阅,在转为付费专栏前订阅本专栏的,可以免费订阅付…...
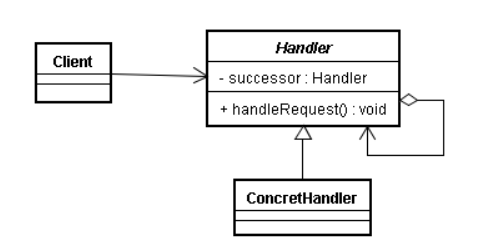
不得不说的行为型模式-责任链模式
目录 责任链模式: 底层原理: 代码案例: 下面是面试中可能遇到的问题: 责任链模式: 责任链模式是一种行为型设计模式,它允许多个对象在一个请求序列中依次处理该请求,直到其中一个对象能够…...
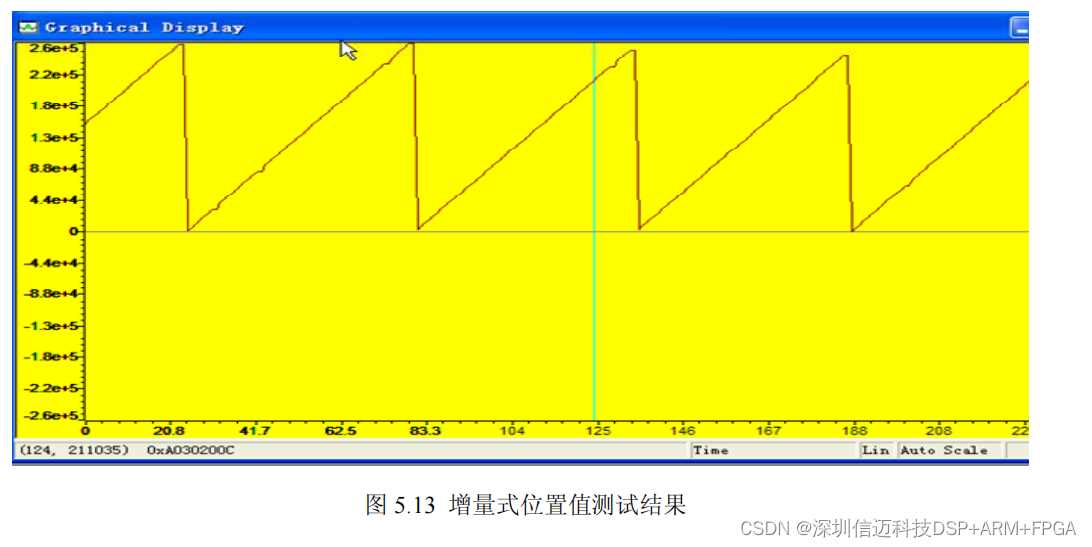
基于dsp+fpga+AD+ENDAC的半导体运动台高速数据采集电路仿真设计(四)
整个调试验证与仿真分析分三个步骤:第一步是进行 PCB 检查及电气特性测试,主 要用来验证硬件设计是否正常工作;第二步进行各子模块功能测试,包括高速光纤串行 通信的稳定性与可靠性测试, A/D 及 D/A 转换特性测…...

快速搭建Electron+Vite3+Vue3+TypeScript5脚手架 (无需梯子,快速安装Electron)
一、介绍 😆 😁 😉 Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个 JavaScript 代码代码库并创建 在Windows上运行的跨平台应用 macOS和Linux——不需…...
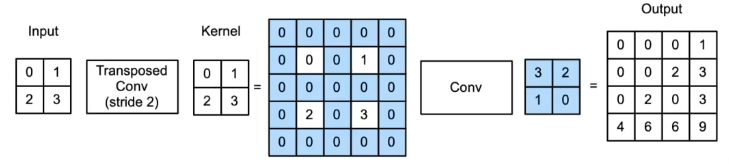
语义分割学习笔记(二)转置卷积
目录 1.转置卷积Transposed Convolution概念 2.转置卷积操作步骤 3.转置卷积参数 4.实战案例 推荐课程:转置卷积(transposed convolution)_哔哩哔哩_bilibili 感谢霹雳吧啦Wz,真乃神人也。 1.转置卷积Transposed Convolutio…...

docker运行PostgreSQL数据库维护,执行脚本备份数据库与更新表结构
文章目录 PostgreSQL简介业务场景数据库维护docker-compose配置备份脚本更新表结构脚本 PostgreSQL简介 PostgreSQL是一种开源的关系型数据库管理系统,它是一个功能强大、高度可定制化和支持复杂应用的数据库。它支持广泛的数据类型,包括数值、文字、二…...

【计算机网络】127.0.0.1、0.0.0.0、localhost地址是什么?
目录 0.0.0.0是什么?127.0.0.1是什么?用途 localhost是什么?总结 0.0.0.0是什么? IPV4中,0.0.0.0地址被用于表示一个无效的,未知的或者不可用的目标。 在服务器中,0.0.0.0指的是本机上的所有I…...

分享2款CSS3母亲节主题寄语文字动画特效
目录 ❤️ 前言 第一款:妈妈您辛苦了! 一、效果图 二、代码实现 第二款:Mothers Day! 一、效果图 二、代码实现 ❤️ 祝福 ❤️ 前言 母亲节,在每年五月的第二个星期日,是用来感谢母亲的节日。…...

【AutoGPT】AutoGPT出现,是否意味着ChatGPT已被淘汰
Yan-英杰的主页 悟已往之不谏 知来者之可追 C程序员,2024届电子信息研究生 目录 前言 什么是ChatGPT? 什么是AutoGPT? AutoGPT与ChatGPT的区别 AutoGPT的优势和劣势 优势 劣势 ChatGPT是否会被淘汰? 前言 近年来&#x…...
( 字符串) 9. 回文数 ——【Leetcode每日一题】
❓9. 回文数 难度:简单 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例如…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
