离散数学集合论
集合论
主要内容
-
集合基本概念
- 属于、包含
- 幂集、空集
- 文氏图等
-
集合的基本运算
- 并、交、补、差等
-
集合恒等式
- 集合运算的算律,恒等式的证明方法
集合的基本概念
集合的定义
集合没有明确的数学定义
理解:由离散个体构成的整体称为集合,称这些个体为集合的元素
常见的数集:N,Z,Q,R,C等分别表示自然数,整数,有理数,实数,负数集合
集合表示法
枚举法–通过列出全体元素来表示集合
谓词表示法–通过谓词概括集合元素的性质
实例 枚举法自然数集合N={0,1,2,3…}
谓词法 S={x|x是实数 ,x^2-1=0}
元素和集合
- 集合的元素具有的性质
- 无序性:元素列出的顺序无关
- 相异性:集合的每个元素只计数一次
- 确定性:对任何元素和集合都能确定这个元素是否为该集合的元素
- 任意性:集合的元素也可以是集合
- 元素与集合的关系
- 隶属关系
- 集合的树形层次结构A={{a,b},{b},d}
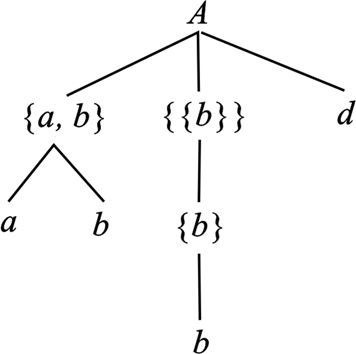
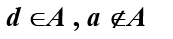
集合与集合
集合与集合之间的关系
⊆ , = , ⊊ , ≠ , ⊂ \subseteq ,=,\subsetneq,\neq, \sub ⊆,=,⊊,=,⊂
定义6.1 幂集
实例 计数,如果|A|=n,则 幂集的个数为2^n
全集E:包含了所有集合的集合 全集具有相对性,与问题有关,不存在绝对的全集
以下描述的集合是什么?(U表示论域)
集合的运算
初级运算
集合的基本运算有 并
相对补 A-B ={x|}
对称差 (A-B)∪(B-A)
绝对补集
并和交运算可以推广到有穷个集合上,即

广义运算
集合的广义并与广义交
广义并
文氏图
求1到100之间(包含 1和1000在内)即不能被5 和 6 整除,也不能被8整除的数有多少个?
定义以下集合
1.能够被5整除的数 200个
能够被6整除的数 166个
能够被8整除的数 125个
按照荣次原理,需要将能够被 5和6 ,5和8 6和8 同时整除的数减去,在加上同时能够被5 6 8整除的数,具体计算可参考下面的公式
不被5 6 8整除的数 = 总数-(能够被5整除的数+能够被6整除的数+能够被 8整除的数) -
容斥原理
- 容斥原理是组合数学中的一个重要原理,他在技术问题中占有很重要的地位
- 容斥原理所研究的问题是与若干有限集的交、并、或差有关的计数
- 在实际工作中,有时需要计算某种性质的元素个数
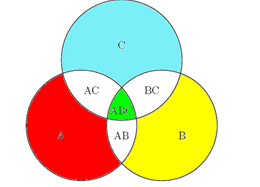
求不超过20的正整数中2或3的倍数的个数
2的倍数
对于求两个有限集合A和B的并集的元素数目
定理1 |A∪B|=|A|+|B|-|A∩B|
即具有性质A或B的元素的个数 等于具有性质A的元素个数和具有兴致B的元素个数的和,减去同时具有性质A和B的元素个数
计算1到700之间能被7整除的整数个数
直接计算相当麻烦,间接计算非常容易
先计算1到700之间能够被7整除的整数个数700/7=100
所以1到700之间不能被7整除的整数个数 700-100=600
逆向思维方式
一个学校只有三门课程:数学、物理、化学。已知修这三门课的学生分别有170、130、120人,同时修数学、物理的学生45人,同时修数学、化学的20人;同时修物理、化学22人,同时修三门课的三人,假设每个学生至少修一门课,问这学校共有多少学生?
令A、B、C分别为修数学、物理、化学的学生集合
|A∪B∪C|
=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C|
=170+130+120-45-22-20+3=336
即学校共有336名学生
对于一般的n个有限集合
错位排列问题
在一个餐厅里,新雇员寄存了N个人的帽子,忘记把寄存号放在帽子上。当顾客取回他们的帽子时,这个雇员从剩下的帽子中随机选择发给他们。问没有一个人收到自己帽子的概率
这本质上就是一个错排问题。
当n=1时,{1}的全排列只有一个(1),他不是错位 所以D1=0
当n=2时,{1,2}的全排列有两个(1,2) 和(2,1)
前者不是错位,后者是错位,所以D2=1
当n=3时,{1,2,3}的全排列有6个
{1,2,3}{1,3,2}{3,2,1}{2,1,3},{3,1,2}{2,3,1}
前4个不是错位,后两个是错位 所以D3=2
全错位排列计数
n 个元素依次给以标号1,2…n N个元素的全排列中,求每个元素都不在自己原来位置上的排列数
设Ai为数i在第i位上的全体排列, i=1,2…n
注:总的排列数为n!
故总的错位排列数为

Ai在原来位置上,则Ai不能动,因而有
|Ai|=(n-1)! ,i=1,2…n
同理
|Ai∩Aj|=(n-2)!,i = 1,2,…,n i!=j
由于是错排,这些排列应排除
但是此时把同时有两个数不错排的排列多排除了一次,在补上时,把同时有三个数不错排的排列多补上了一次,应排除。。继续这一过程,得到错排的排列种数
每个元素都不在原来未知的排列数
例子:在8个字母ABCDEFGH的全排列中,求使得ACEG四个字母不在原来上的错排数目
8个字母的全排列中,令A1 A2 A3 A4 分别在ACEG在原来位置上的排列
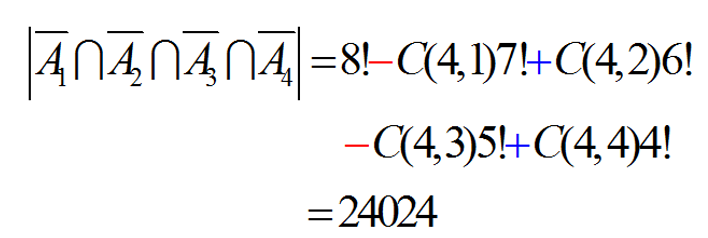
二元关系
- 有序对与笛卡尔积
- 二元关系的定义与表示法
- 关系的运算
- 关系的性质
- 关系的闭包
- 等价关系与划分
- 偏序关系
有序对与笛卡尔积
定义7.1由两个元素x和y,按照一定的顺序组成的二元组称为有序对,记作<x,y>
有序对性质
- 有序性<x,y>不等<y,x>(当x不等y)
- <x,y>与<u,v>相等的充分必要条件是
<x,y>=<u,v> <=> x=u并且y=v
7.2
笛卡尔积
设A,B为集合,A与B的笛卡尔积记作AxB,且AxB={<x,y>|x∈A并且y属于B}
例子1
A={1,2,3} B={a,b,c}
AxB
={<1,a>,<1,b>,<1,c>,<2,a>,<2,b>,<2,c><3,a>,❤️,b>,❤️,c>}
BxA
={<a,1>,<b,1>,<c,1>,<a,2>,<b,2>,<c,2>,<a,3>,<b,3>,<c,3>}
A={∅} B={∅}
P(A)xA={<∅,∅>,<{∅},∅}
P(A)xB=∅
笛卡尔积的性质
不适合交换律
不适合结合律
对于并或交与运算满足分配律
若A或B有一个为空集,则AXB就是空集
二元关系
如果一个集合满足以下条件之一
集合非空,且他的元素都是有序对
集合是空集
则称该集合为一个二元关系,简称为关系,记作R
如果<x,y>∈R,可记作xRy,如果<x,y>不属于R,则记作 x y
实例 R={<1,2>,<a,b>}
S={<1,2>,a,b}
R是二元关系,当a,b不是有序对时,S不是二元关系
根据上面的写法,可以写1R2 aRb a c等
A到B的关系与A上的关系
定义7.4
设AB为集合,AXB的任何自己所定义的二元关系叫做A到B 的二元关系当A=B的时候叫做A上的二元关系
例三
A={0,1} B={1,2,3}那么
R1={0,2}R2=AXB R3=∅ R4={<0,1>}
R1,R2,R3,R4是从A到B的二元关系
R3和R4也是A上的二元关系
计数:|A|
|AxA|=n^2 AxA的自己有多少个 所以A上有2n2
例如A=3,则A上有 512个不同的二元关系
A上重要关系的实例
定义7.5设A为集合
空集 A上的关系,称为空关系
全域关系Ea={<x,y>|x∈A并且y∈A}=AXA
恒等关系Ia={<x,x>|x∈A}
小于等于关系Ia={<x,y>|x,y∈A并且x≤y}A为实数子集
整除关系 Da={<x,y>|x,y∈A并且x整除y}A为非0的整数子集
包含关系R属 ={<x,y>∈A并且x}A是集合族
例如A={1,2}则
EA={<1,1>,<1,2>,<2,1>,<2,2>}
IA={<1,1><2,2>}
例如A={1,2,3}B={a,b}
则lA={<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,❤️,3>}
DA={<1,1>,<1,2>,<1,3>,<2,2>,❤️,3>}
A=P(B)={∅,{a},{b},{a,b}}则A上的包含关系
<∅,∅>,<∅,{a}>,<∅,{b}> <∅,{a,b}>,<{a},{a}>,<{a},{a,b}>
<{b},{b}>,<{b},{a,b}>,<{a,b}{a,b}>
关系的运算
关系的基本运算
关系的定义域、值域与域分别定义为
dom={x|存在y(<x,y>∈R)}
ranR={y|存在x(<x,y>∈R)}
fldR=domR∪ranR
例如R={<1,2>,<1,3>,<2,4>,<4,3>}
domR={1,2,4}
ranR={2,3,4}
fldR={1,2,3,4}
关系运算(逆与合成 )
关系的逆运算
R-1={<y,x>|<x,y>∈R}
关系的合成运算
FOG={<x,y>|存在t(<x,t>∈F∩<t,y>∈G)}
R={<1,2>,<2,3>,<1,4>,<2,2>}
S={<1,1>,<1,3>,<2,3>,❤️,2>,❤️,3>}
R-1={<2,1>,❤️,2>,<4,1>,<2,2>}
ROS={<1,3>,<2,2>,<2,3>}
SOR={<1,2>,<1,4>,❤️,3>,❤️,2>}
关系运算(限制与像)
设R是二元关系,A是集合
R在A上的限制记作R↾A 其中
R↾A={<x,y>|xRy并且x∈A}
A在R上的像记作R[A]其中,R[A]=ran(R↾A)
说明
R在A上的限制R↾A是R的子关系,及R↾A∈R
A在R上的像R[A]是ranR的子集,即R[A]属于ranR
例子R={<1,2>,<1,3>,<2,2>,<2,4>,❤️,2>}则
R={<1,2>,<1,3>,<2,2>,<2,4>,❤️,2>}则
R↾{1}={<1,2>,<1,3>}
R↾∅=∅
R↾{2,3}={<2,2>,<2,4>,❤️,2>}
R[{1}]={2,3}
R[∅]=∅
R[{3}]={2}
关系运算的性质
设F是任意的关系,则(F-1)-1=F
domF-1=ranF,ranF-1=domF
设F,G,H是任意的关系,则
(FoG)oH=Fo(GoH)
(FoG)-1=G-1 o F -1
关系的幂运算
设R为A上的关系,n为自然数,则R的n次幂定义为:
R0={<x,x>|x∈A}=IA
Rn+1=RnoR
注意
对于A上的任何关系R1和R2都有R10=R20=IA
对于A上的任何关系R都有R1=R
幂的求法
设A={a,b,c,d}R={<a,b>,<b,a>,<b,c>,<c,d>}
求R的各次幂,分别用矩阵和关系图表示
R与R^2的关系矩阵分别是
关系的性质
设R为A上的关系
若Vx(x∈A-><x,x>∈R),则称R在A上是自反的
若Vx(x∈A-><x,x>∉R),则称关系R在A上是反自反的
实例
自反:全域关系Ea 恒等关系Ia 小于等于关系LA,整除关系DA
反自反:实数集上的小于关系,幂集上的真包含关系‘
A={1,2,3} R1,R2,R3是A上的关系,其中
R1={<1,1>,<2,2>}
R2={<1,1><2,2>,❤️,3>,<1,2>}
R3={<1,3>}
R2自反 R3反自反 R1既不是自反的也不是反自反的
对称性与反对称
定义7.12设R为A上的关系
1.若VxVy(x,y∈A^<x,y>∈R-><y,x>∈R)则称R为A上对称的关系
若若VxVy(x,y∈A^<x,y>∈R-><y,x>∈R->x=y)则称R为A上的反对称关系
实例:对称关系A上的全域关系Ea 恒等关系IA 和空关系
反对称关系 恒等关系IA和空关系也是A上的反对称关系
设A={1,2,3} R1,R2,R3,R4都是A上的关系,其中
R1={<1,1>,<2,2>}
R2={<1,1><1,2>,<2,1>}
R3={<1,2>,<1,3>}
R4={<1,2>,<2,1>,<1,3>}
R1:对称和反对称
R2只有对称
R3:只有反对称
R4:不对称,不反对称
传递性
定义7.13设R为A上的关系,若
任意x任意y任意z(x,y,z属于A并且<x,y>属于R并且<y,z>∈R-><x,z>∈R)
则称R是A上的传递关系
实例:A上的全域关系EA,恒等关系IA和空关系∅,小于等于关系,整除关系,包含与真包含关系
设A={1,2,3}R1,R2,R3是A上的关系,其中
R1={<1,1>,<2,2>}
R2={<1,2>,<2,3>}
R3={<1,3>}
R1和R3是A上的传递关系,R2不是A上的传递关系
关系性质成立的充要条件
设R为A上的关系,则
- R在A上自反当且仅当IA是R的子集
- R在A上反自反当且仅当R∩IA=∅
- R在A上对称当且仅当R=R-1
- R在A上反对恒当且仅当R∩R-1是IA的子集
- R在A上传递当且仅当ROR是R的子集
关系性质的三种等价条件
| 自反性 | 反自反性 | 对称性 | 反对称性 | 传递性 | |
|---|---|---|---|---|---|
| 集合 | Ia是R的子集 | R∩IA=∅ | R=R-1 | R∩R-1是IA的子集 | ROR是MR的子集 |
| 关系矩阵 | 主对角线元素全是1 | 主对角元素全是0 | 矩阵是对称矩阵 | rij=1 **且i≠j*,** 则rji=0 | |
| 关系图 | 每个顶点都有环 | 每个顶点都没有环 | 两点之间有边,是一对方向相反的边 | 两点之间有边,是一条有向边 | 点xi到xj有边,到有边,则xi到也有到边j |
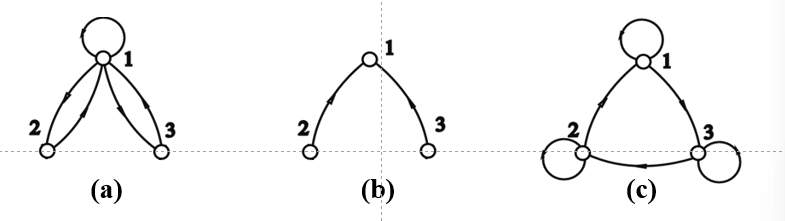
对称(两点之间有边,是一对方向相反的边)
反自反(每个顶点都没有环)、反对称(两点之间有边,是一条有向边)、传递
c自反, 反对称
关系的闭包
主要内容
- 闭包定义
- 闭包的构造方法
- 集合表示
- 矩阵表示
- 图表示
- 闭包的性质

一个对象

对象的圆闭包,橘黄色圈,满足
1,是圆的(性质)
2,包含所给对象
3,如果有个绿色圆也能包含该对象,就一定也能够包含这个橘黄圈
对象的正方形闭包,蓝色框,满足

1.是正方形的
2.包含所给对象
3.如果有个红色正方形也能包含该对象,就一定也能包含这个 青涩狂
闭包定义
定义7.4设R是非空集合A上的关系,R的自反(对称或传递)闭包是A上的关系R’,使得R’满足以下条件
- R‘是自反的(对称的或传递的)
- R是R’的子集
- 对A上任何包含R的自反(对称或传递)关系R’’ 有R’是R’’ R的自反闭包记作r®,对称闭包记作s®,传递闭包记作t®
定理7.10 设R为A上的关系,则有
- r®=R∪R0=R∪IA
- s®=R∪R-1
- t®=R∪R2∪R3…并RN
说明对有穷集A(|A|=n)上的关系,(3)中的并最多不超过Rn
**例子9 **
设A={a,b,c,d},R={<a,b>,<b,a>,<b,c>,<c,d>,<d,b>}
R和r®,s®,t®的关系图如下图所示
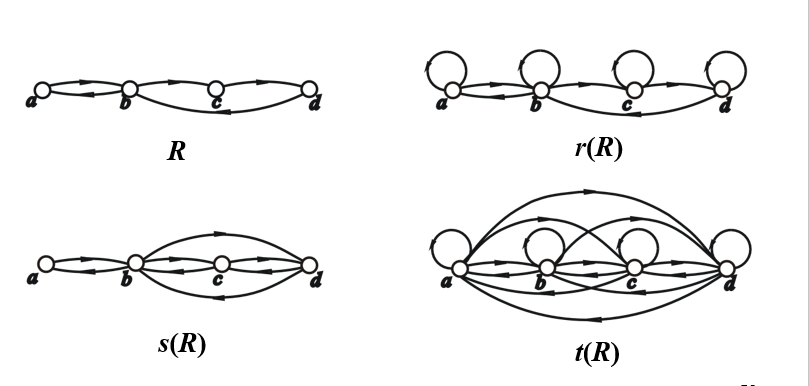
求传递闭包的算法
算法warshall
输入:M(R的关系矩阵)
输出:MT(t®的关系矩阵)
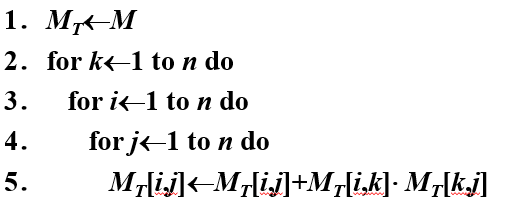
实例
设A={a,b,c,d}R={<a,b>,<b,a>,<b,c>,<c,d>,<d,b>}
R 的传递闭包的矩阵如下
M0
闭包的性质
定理7.11 设R是非空集合A上的关系则
(1)R是自反的当且仅当r®=R
(2)R是对称的当且仅当s®=R
(3)R是传递的,当且仅当t®=R
7.12设R1和R2是非空集合A上的关系,且R1是R2的子集,
则r(R1)是r(R2)子集,同理对于对称闭包与传递比表也是类似的
定理7.13设R是非空集合A上的关系
- 若R 是自反的,则s®与t®也是自反的
- 设R是对称的,r®与t®也是对称的
- 若R是传递的,则r®是传递的
证明,如果需要进行多个闭包运算,比如求R的自反,对称,传递的闭包tsr®运算顺序如下
tsr®=rts®=trs®
7.6等价关系与划分
- 等价关系的定义与实例
- 等价类及其性质
- 商集与集合的划分
- 等级关系与划分的一一对应
定义7.15设R是非空集合A上的关系,如果R是自反的,对称的和传递的,则称R为A上的等价关系,设R是一个等价关系,若<x,y>∈R,则称x等价于y。记作x~y
实例 A={1,2…8}如下定义A上的关系R
R={<x,y>|x,y∈A并且x与y模3 相等,即x除以3的余数与y除以3的余数相等,不难验证R为A上的等价关系,因为}
- 任意x∈A,有x=x(mod3)
- 任意x,y∈A,若x=y(mod3)则有y=x(mod3)
- 任意x,y,z∈A,若x=u(mod3),y=z(mod3),则有x=z(mod3)
模3等价关系的关系图
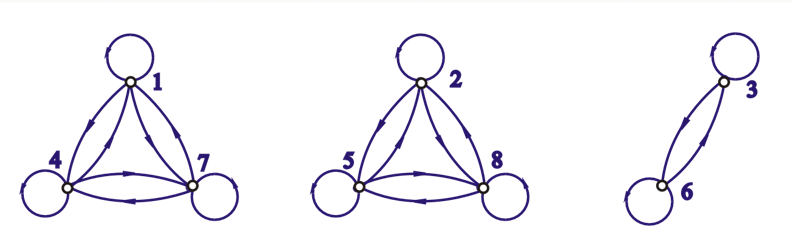
等价关系的关系矩阵与关系图
关系矩阵
- 主对角线元素等于1
- 对称矩阵
- MR=MRn
关系图
- 每一节点都有一自划线
- 如果有从a到b的弧,那么也有从b到a的弧
- 如果有从a到c有一条路径,则从a到c有一条弧
等价类定义
定义7.16设R 为非空集合A上的等价滚西,任意x∈A,令[x]R={y|y∈A交xRy}
称[x]R为x关于R的等价类,简称为x的等价类,简称为[x]
实例 A={1,2,,8}上模3等价关系的 等价类
[1]=[4]=[7]={1,4,7}
[2]=[5]=[8]={2,5,8}
[3]=[6]={3,6}
定理7.14设R是非空集合A上的等价关系,则
- 任意x∈A,[x]是A上的非空子集
- 任意x,y属于A,如果xRy,则[x]=[y]
- 任意x,y∈A,如果x
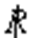 y,则[x]与[y]不交
y,则[x]与[y]不交 - ∪{|x|x∈A}=A
商集与划分
定义7.14设R为非空集合A上的等价关系,以R的所有等价类作为元素的集合称为A关于R上的商集,记作A/R
A/R={[x]R|x∈A}
实例 设A={1,2,…8}A关于模3等价关系的 商集为
A/R={{1,4,7},{2,5,8},{3,6}}
A关于恒扥关系和全域关系的商集为
A/IA={{1},{2}…,{8}}
A/EA={{1,2,…,8}}
定义7.18设A为非空集合,若A的子集组π(π是P(A)的子集)满足
1.∅∉π
2.任意x任意y(x,y∈π交x≠y->x∩y=∅)
∪π=A
则称π是A的一个划分,称π中的元素为A的划分快
划分实例
设A={a,b,c,d}给定π1={{a,b,c},{d}}
π2={{a,b},{c},{d}}
π3={{a},{a,b,c,d}}
π4={{a,b},{c}}
π5={∅{,a,b},{c,d}}
π6={{a,{a}},{b,c,d}}
π1和π2是A的划分,其他都不是A的划分
实例
给出A={1,2,3}上所有的等价关系
解:先做出A的划分,从左到右分别记作π1,π2,π3,π4,π5

π1对应EA,π5对应IA,π2,π3和π4分别对应R2,R3,R4
R2={<2,3>,❤️,2>}∪IA
R3={<1,3>,❤️,1>}∪IA
R4={<1,2>,<2,1>}∪IA
偏序关系
主要内容
偏序关系
- 偏序关系的定义
- 偏序关系的实例
偏序集与哈斯图
偏序集中特殊元素及其性质
极大元、极小元、最大元、最小元、上界、下界、最小上届,最小下界
7.19偏序关系非空集合A上的自反,反对称和传递的关系
记作≤,设≤为偏序关系,如果<x,y>∈≤,则记作x≤y,读作x小于或等于 y
实例
集合A上的恒扥关系IA也是A上的偏序关系
小于或等于关系,整除关系和包含关系也是相应集合上的偏序关系
定义7.20设R为非空集合A上的偏序关系
- x,y∈A,x与y可比等价x≤y或y≤x
- 任取元素x和y,可能有以下几种情况发生 x<y 或 y<x x=y,x与y是不可比的
定义7.21R为非空集合的偏序关系
任意x,y∈A,x与y都是可比的,则称R为全序
实例:数集上的小于等于关系是全序关系,整除关系不是正整数集合上的全序关系
定义7.22x,y∈A,如果x<y且不存在z∈A使得x<z<y则称y覆盖x
例如{1,2,4,6}集合上整除关系,2覆盖1,4,和6,覆盖2,4不覆盖1
定义7.23集合A和A上的偏序关系≤一起叫做偏序集,记作<A,≤>
实例<Z,≤>,<P(A),R属于>
哈斯图:利用偏序关系的自反、反对称、传递性进行简化的关系图
特点
每个节点没有环
两个连通的节点之间的序关系通过节点位置的高低表示,位置低的元素的顺序在前
且 有覆盖关系的两个节点之间连边
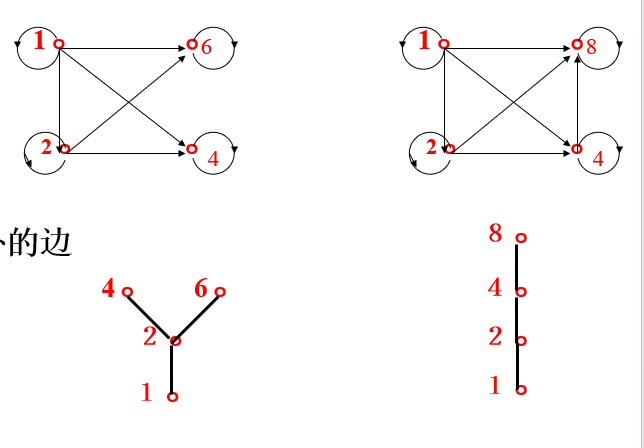
- 去环
- 去覆盖以外的边
- 重新排列
- 去剪头
例子
偏序集<{2,3,6,12,24,36},R整除>和<P({a,b,c}),R属于>的哈斯图
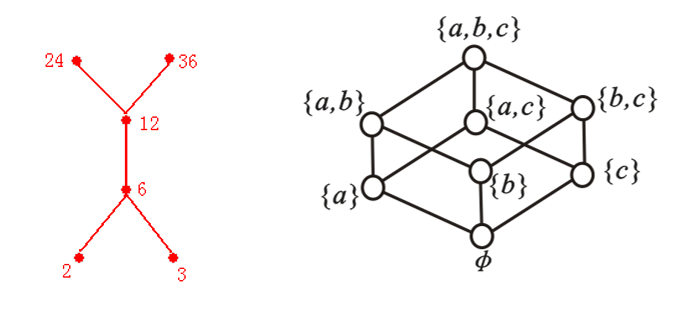
例子:已知偏序集<A,R>的哈斯图如下图所示,试求出集合A和关系R的表达式
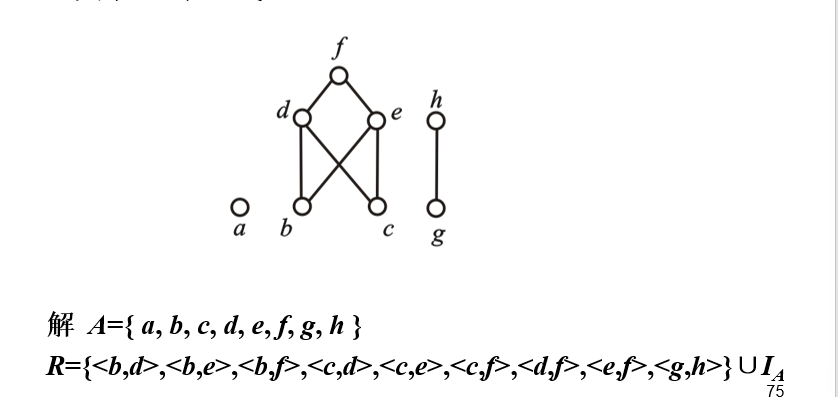
偏序集中的特殊关系
定义7.24设<A,≤>为偏序集,B是A的子集,y∈B
- 若任意x(x∈B->y<=x)成立,则称y为B的最小元
- 若任意x(x∈B->y>=x)成立,则称y为B的最大元
- 若任意x(x∈B并且x<=y->x=y)成立,则称y为B的极小元
- 若任意x(x∈B并且y<=x->x=y)成立,则称y为B的极大元
性质
- 对于有穷集,极小元和极大元一定存在,可能存在多个
- 最小元和最大元不一定存在,如果存在一定唯一
- 最小元一定是极小元,最大元一定是极大元
- 孤立点即是极小元,也是极大元
偏序集中的特殊元素
- 若任意x(x∈B->x<=y)成立,则称y为B的上界
- 若任意x(x∈B->y<=x)成立,则称y为B 的下界
- 令C={y|y为B的上界},C的最小元为B的最小上界偶上确界
- 令D={y|y为B的下界},D的最大元为B的最大下界或下确界
性质
- 下界、上界、下确界、上确界不一定存在
- 下界、上界存在不一定唯一
- 下确界、上确界如果存在,则唯一
- 集合的最小元是其下确界,最大元是其上确界,反之不对
实例
设偏序集<A,≤>求A的极小元、最小元、极大元,最大元,设B={b,c,d}求B的下界,上界,下确界,上确界

解:
极小元:a,b,c,g
极大元:a,f,h
没有最小元和最大元
B的下界和最大下界都不存在
上界 d和f
最小上界为d
实例
某偏序关系的哈斯图如右图所示,讨论当B 取相应集合时,其最大元,最小元,极大元,极小元,上/下界,上/下确界
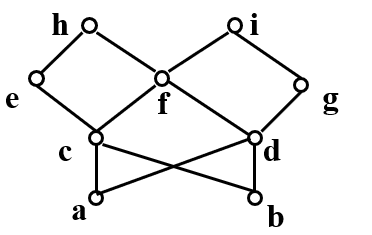
| B | 极小元 | 极大元 | 最小元 | 最大元 |
|---|---|---|---|---|
| {a,b} | a,b | a,b | 无 | 无 |
| {a,b,c} | a,b | c | 无 | c |
| {a,b,c,d} | a,b | c,d | 无 | 无 |
| {b,c,d,f} | b | f | b | f |
| {a,c,f,i} | a | i | a | i |
| B | 上界 | 下界 | 上确界 | 下确界 |
|---|---|---|---|---|
| {a,b} | c,d,e,f,g,h,i | 无 | 无 | 无 |
| {a,b,c} | c,e,f,h,i | 无 | c | 无 |
| {a,b,c,d} | f,h,i | 无 | f | 无 |
| {b,c,d,f} | f,h,i | b | f | n |
| {a,c,f,i} | i | a | i | a |
习题
设A={1,2,3}R={<x,y>|x,y∈A且x+2y<=6},S={<1,2>,<1,3>,<2,2>}
求R 的集合表达式
R-1
domR,ranR,fldR
ROS,R^3
r®,s®,t®
- R={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>}
- R-1={<1,1>,<2,1>,<1,2>,<2,2>,<1,3>}
- domR={1,2,3}ranR={1,2},fldR={1,2,3}
- RoS={<1,2>,<1,3>,<2,2>,<2,3>,❤️,2>,❤️,3>}
- R^3={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,❤️,2>}
r®={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,❤️,3>}
s®={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,<1,3>}
t®={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,❤️,2>}
设偏序集<A,R>的哈斯图如下所示
写出A和Rd的集合表达式
求该偏序集中的极大元,极小元,最大元,最小元
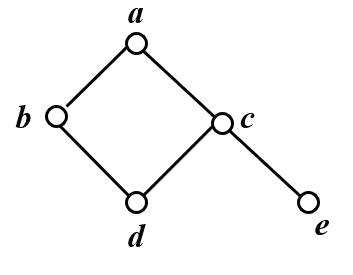
A={a,b,c,d,e}
R={<d,b>,<d,a>,<d,c>,<e,c>,<e,a>,<b,a>,<c,a>}并Ia
极大元和最大元是a
没有最小元
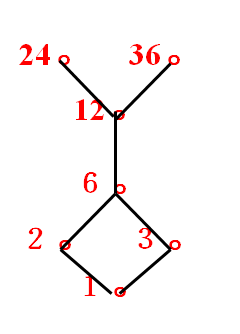
| B | 极小元 | 极大元 | 最小元 | 最大元 | 上界 | 上确界 | 下界 | 下确界 |
|---|---|---|---|---|---|---|---|---|
| {2,3} | 2,3 | 2,3 | 无 | 无 | 6,12,24,36 | 6 | 1 | 1 |
| {1,2,3} | 1 | 2,3 | 1 | 无 | 6,12,24,36 | 6 | 1 | 1 |
| {6,12,4} | 6 | 24 | 6 | 24 | 24 | 24 | 1,2,3,6 | 6 |
| A | 1 | 24,36 | 1 | 无 | 无 | 无 | 1 | 1 |
例题4
设R是Z上的模n等价关系,即x~y<=>x=y(modn)试给出由R确定的Z的划分π
设除以n余数为r的整数构成等价类[r],则[r]={kn+r|k∈z},r=0,1,…,n-1
π={[r]|r=0,1,…,n-1}
例题5
设R是A上的二元关系,设S={<a,b>|存在c(<a,c>∈R交<c,b>∈R)}证明如果RE是等价关系,则S也是等价关系
证:R是A上的等加固韩系
相关文章:

离散数学集合论
集合论 主要内容 集合基本概念 属于、包含幂集、空集文氏图等 集合的基本运算 并、交、补、差等 集合恒等式 集合运算的算律,恒等式的证明方法 集合的基本概念 集合的定义 集合没有明确的数学定义 理解:由离散个体构成的整体称为集合,…...

TypeScript 基础
类型注解 类型注解:约束变量的类型 示例代码: let age:number 18 说明:代码中的 :number 就是类型注解 解释:约定了类型,就只能给变量赋值该类型的值,否则,就会报错 错误演示:…...

MySQL InnoDB引擎 和 Oracle SGA
MySQL InnoDB引擎和Oracle SGA有以下异同: 异同点: 两者都是用来管理数据存储和访问的。 它们都可以通过调整参数来优化性能。 它们都支持事务处理和ACID属性。 它们都可以通过备份和恢复来保护数据。 异点: MySQL InnoDB引擎是一种存储…...
JAVA开发与运维(web生产环境部署)
web生产环境部署,往往是分布式,和开发环境或者测试环境我们一般使用单机不同。 一、部署内容 1、后端服务 2、后台管理系统vue 3、小程序 二、所需要服务器 5台前端服务器 8台后端服务 三、所需要的第三方组件 redismysqlclbOSSCDNWAFRocketMQ…...

普通人,自学编程,5个必备步骤
天给大家分享个干货哈 普通人自学编程 想学成找到一份工作甚至进大厂 非常有效且必备的5个步骤 文章最后 还给大家提供了一些免费的学习资料 记得提前收藏起来 相信很多人在最开始学编程的时候 上来就是去网上找一套视频 或者买一本书直接开干 这种简单粗暴的方法其实是不对的 …...

kubernetes安全框架RBAC
目录 一、Kubernetes 安全概述 二、鉴权、授权和准入控制 2.1 鉴权(Authentication) 2.2 授权(Authorization) 2.3 准入控制 三、基于角色的权限访问控制: RBAC 四、案例:为指定用户授权访问不同命名空间权限 一、Kubernetes 安全概述 K8S安全控…...
)
【大数据面试题大全】大数据真实面试题(持续更新)
【大数据面试题大全】大数据真实面试题(持续更新) 1)Java1.1.Java 中的集合1.2.Java 中的多线程如何实现1.3.Java 中的 JavaBean 怎么进行去重1.4.Java 中 和 equals 有什么区别1.5.Java 中的任务定时调度器 2)SQL2.1.SQL 中的聚…...

Linux [常见指令 (1)]
Linux常见指令 ⑴ 1. 操作系统1.1什么事操作系统1.2选择指令的原因 2.使用工具3.Linux的指令操作3.1mkdir指令描述:用法:例子 mkdir 目录名例子 mkdir -p 目录1/ 目录2/ 目录3 3.2 touch指令描述:用法:例子 touch 文件 3.2pwd指令描述:用法:例子 pwd 3.4cd指令描述:用法:例子 c…...
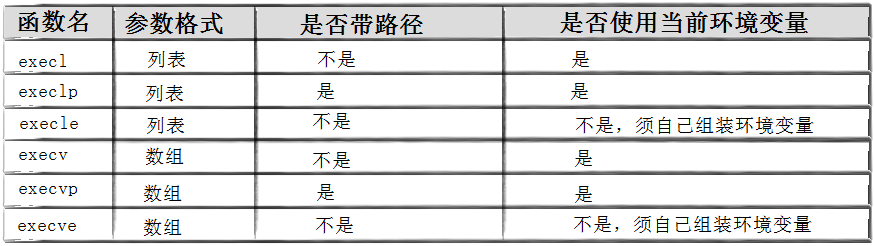
进程控制下篇
进程控制下篇 1.进程创建 1.1认识fork / vfork 在linux中fork函数时非常重要的函数,它从已存在进程中创建一个新进程。新进程为子进程,而原进程为父进程 #include<unistd.h> int main() {pid_t i fork;return 0; }当前进程调用fork,…...

PS学习笔记(零基础PS学习教程)
很多新手学习PS不知从何下手,做设计的第一阶段肯定是打牢基础,把工具用熟练;本期特别为大家整理了PS入门的学习笔记,把每个工具的用法整理了下来,在使用过程中有哪里不清楚的可以翻看来看看~ 一、ps的工作界面的介绍 …...

如何构建数据血缘系统
1、明确需求,确定边界 在进行血缘系统构建之前,需要进行需求调研,明确血缘系统的主要功能,从而确定血缘系统的最细节点粒度,实体边界范围。 例如节点粒度是否需要精确到字段级,或是表级。一般来说&#x…...

IPsec中IKE与ISAKMP过程分析(主模式-消息3)
IPsec中IKE与ISAKMP过程分析(主模式-消息1)_搞搞搞高傲的博客-CSDN博客 IPsec中IKE与ISAKMP过程分析(主模式-消息2)_搞搞搞高傲的博客-CSDN博客 阶段目标过程消息IKE第一阶段建立一个ISAKMP SA实现通信双发的身份鉴别和密钥交换&…...
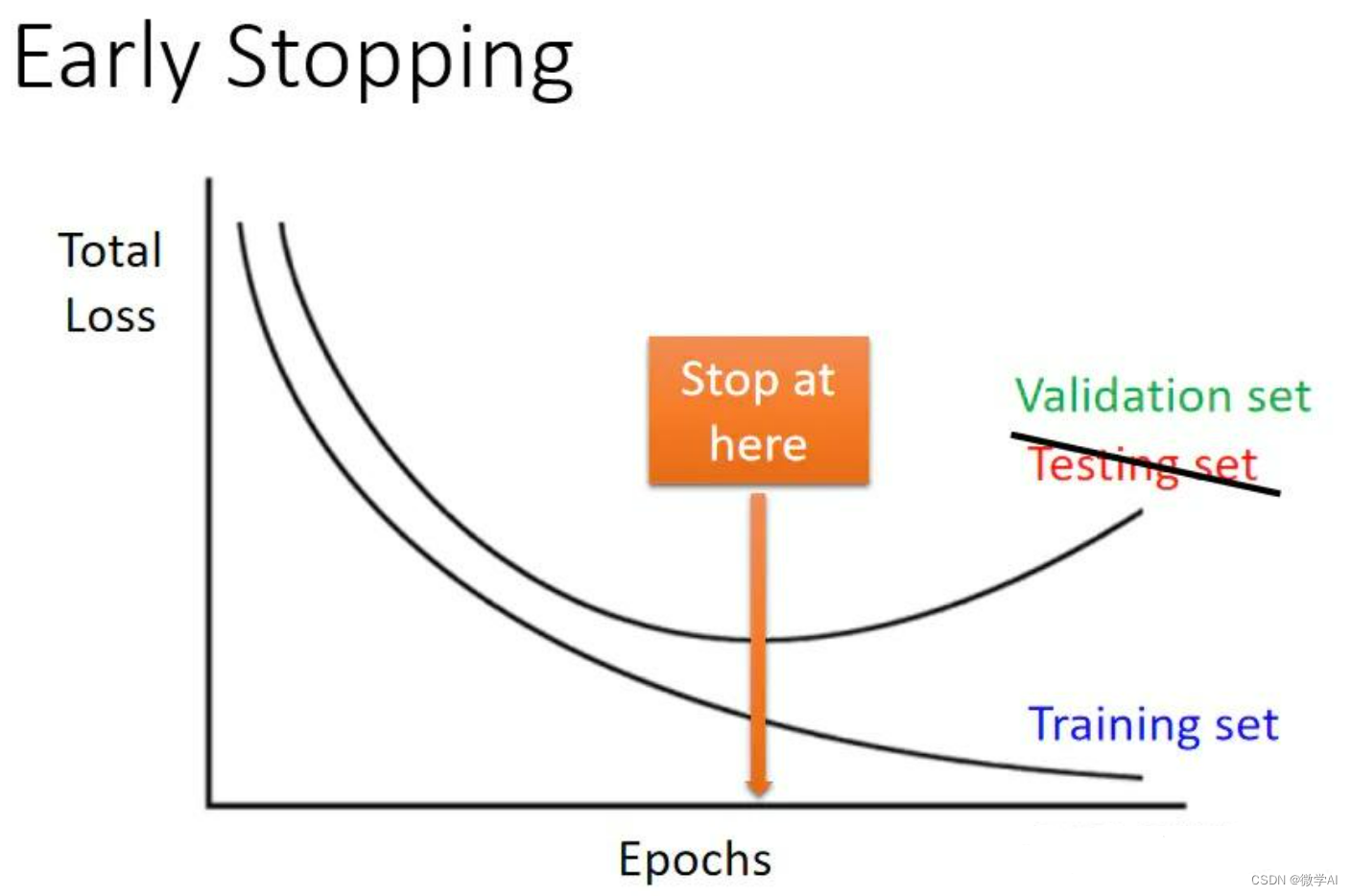
深度学习技巧应用10-PyTorch框架中早停法类的构建与运用
大家好,我是微学AI,今天给大家介绍一下深度学习技巧应用10-PyTorch框架中早停法类的构建与运用,文章将介绍深度学习训练过程中的一个重要技巧—早停法,以及如何在PyTorch框架中实现早停法。文章将从早停法原理和实践出发,结合实际案例剖析早停法的优缺点及在PyTorch中的应…...
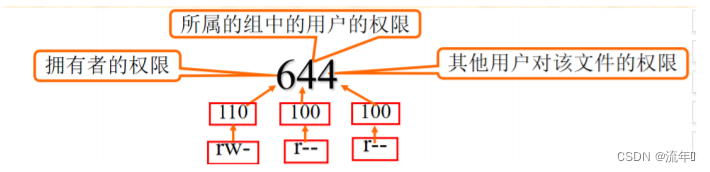
Linux文件系统权限
目录标题 文件权限文件和目录的一般权限文件的权限针对三类对象进行定义文件和目录中,r、w、x的作用 设置文件和目录的一般权限修改文件或目录的权限—chmod(change mode)命令权限值的表示方法—使用3位八进制数表示权限值的表示方法—使用字符串表示修改文件或目录…...

ctfshow之_萌新web1至web7
一、访问在线靶场ctfshow ctf.showhttps://ctf.show/challenges如下图所示,进入_萌新赛的web1问题: 如上图所示,页面代码提示id1000时,可以查询到flag,进行如下尝试: 如下图所示,传入参数id1时…...

HPDA的资料
HPDA,英文全称为High Performance Data Analysis,直译为高性能数据分析。 适用场景 机器学习大数据分析 技术挑战 大量的元数据操作数据的同步随机读写高IOPOS的小IO请求高带宽的文件请求 技术关键字 存算分离移动计算大I/O直通,小I/O聚…...
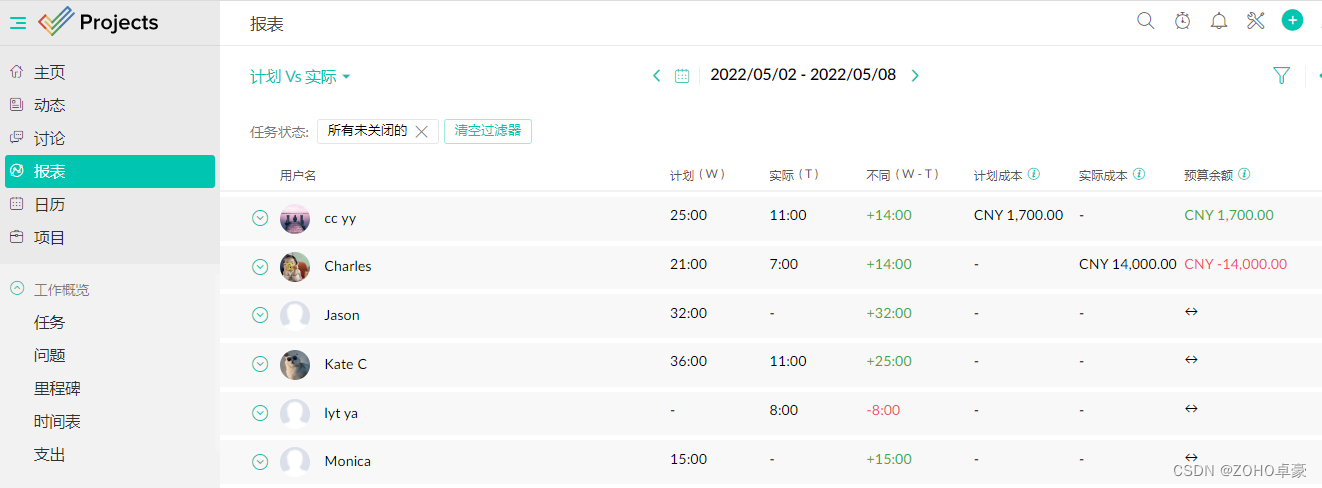
项目管理软件可以用来做什么?这篇文章说清楚了
项目管理软件是用来干嘛的,就得看对项目的理解。项目是为创造独特的产品、服务或成果而进行的临时性工作。建造一座大楼可以是一个项目,进行一次旅游活动、日常办公活动、期末考试复习等也都可以看成一个项目。 项目管理不善会导致项目超时、超支、返工、…...

ETL工具 - Kettle 转换算子介绍
一、Kettle 转换算子 上篇文章对 Kettle 中的输入输出算子进行了介绍,本篇文章继续对转换算子进行讲解。 下面是上篇文章的地址: ETL工具 - Kettle 输入输出算子介绍 转换是ETL里面的T(Transform),主要做数据转换&am…...

界面设计的读书笔记
所见即所得,属于绝大多数的人。 所想即所想,属于极少数的人。 当复杂度,超出了大脑的负荷,人会觉得很累,直到放弃追求。 地图的显示,必须有足够多的描述性的数据。 点信息 :标签,位…...
C#底层库--自定义进制转换器(可去除特殊字符,非Convert.ToString方式)
系列文章 C#底层库–程序日志记录类 本文链接:https://blog.csdn.net/youcheng_ge/article/details/124187709 C#底层库–MySQLBuilder脚本构建类(select、insert、update、in、带条件的SQL自动生成) 本文链接:https://blog.csd…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
