【R语言】鉴于计算10亿以内训练模型记录for循环的加速
文章目录
- 1 前言
- 2 几个循环
- 2.1 100以内的和
- 2.2 100以内奇数和/偶数和
- 3 多重循环
- 3.1 向量化
- 3.2 合并循环
- 3.3 apply函数
- 3.4 矩阵运算
- 3.5 foreach分解任务
- 4 讨论
1 前言
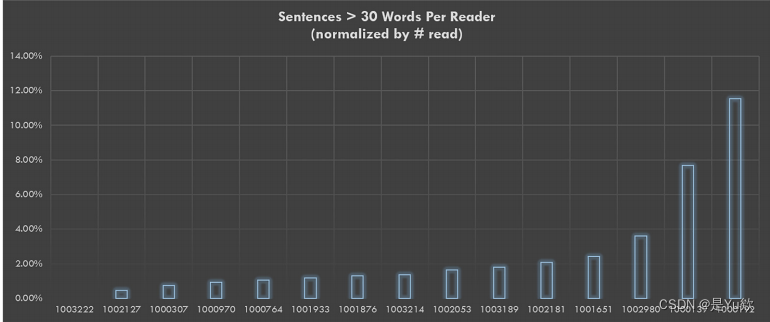
笔者主力机是MBAM1芯片(8+256),某个下午巩固循环突然思考到个问题,小循环很快就能run出来,中循环还勉勉强强,稍微上点强度就运行的很慢。虽然是CPU占用100%,8颗核心好像是偷着懒跑的,但是丢给我那台4核心8线程黑苹果,是跑满的,说明ARM在多线程的时候,有点东西
下图是计算一个10亿内训练模型时的top:

2 几个循环
2.1 100以内的和
### for
sum <- 0
for (i in 1:100) {sum <- sum + i
}
print(sum)### while
sum <- 0
i <- 1
while (i <= 100) {sum <- sum + ii <- i + 1
}
print(sum)
2.2 100以内奇数和/偶数和
### for
odd_sum <- 0
even_sum <- 0for (i in 1:100) {if (i %% 2 == 0) {even_sum <- even_sum + i} else {odd_sum <- odd_sum + i}
}print(paste("奇数和:", odd_sum))
print(paste("偶数和:", even_sum))### while
odd_sum <- 0
even_sum <- 0
i <- 1while (i <= 100) {if (i %% 2 == 0) {even_sum <- even_sum + i} else {odd_sum <- odd_sum + i}i <- i + 1
}print(paste("奇数和:", odd_sum))
print(paste("偶数和:", even_sum))
3 多重循环
以下仅记录和提供思路,具体情况具体分析,但是有一点思维模式很得益
3.1 向量化
假设计算两个向量x和y的点积,使用for循环分别游历,相乘再相加:
x <- c(1, 2, 3, 4, 5)
y <- c(5, 4, 3, 2, 1)
dot_product <- 0
for (i in 1:length(x)) {dot_product <- dot_product + x[i] * y[i]
}
print(dot_product)
向量化,可以理解为对号入座,亮点就是sum()和*:
x <- c(1, 2, 3, 4, 5)
y <- c(5, 4, 3, 2, 1)
dot_product <- sum(x * y)
print(dot_product)
3.2 合并循环
假设对两个矩阵A和B中的每个元素进行遍历,将它们相加,并将结果保存到矩阵C中。可以使用两个嵌套的for循环实现:
A <- matrix(1:9, 3, 3)
B <- matrix(10:18, 3, 3)
C <- matrix(0, 3, 3)
for (i in 1:nrow(A)) {for (j in 1:ncol(A)) {C[i, j] <- A[i, j] + B[i, j]}
}
print(C)#输出结果:[,1] [,2] [,3]
[1,] 11 13 15
[2,] 17 19 21
[3,] 23 25 27
但是理解这类的目的,合并循环的思路在这里刚好就是矩阵一一对应的数字相加:
A <- matrix(1:9, 3, 3)
B <- matrix(10:18, 3, 3)
C <- A + B
print(C)
3.3 apply函数
假设有一个3x3的二维矩阵mat,需要将矩阵中每个元素求平方。我们可以使用for循环来实现:
mat <- matrix(1:9, 3, 3)
result <- matrix(0, 3, 3)
for (i in 1:nrow(mat)) {for (j in 1:ncol(mat)) {result[i, j] <- mat[i, j] ^ 2}
}
print(result)
用apply+function:
mat <- matrix(1:9, 3, 3)
result <- apply(mat, c(1, 2), function(x) x^2)
print(result)3.4 矩阵运算
假设需要计算一个矩阵A的逆矩阵,使用for循环和矩阵运算实现:
A <- matrix(c(1, 2, 3, 4), 2, 2)
det_A <- A[1, 1] * A[2, 2] - A[1, 2] * A[2, 1]
adj_A <- matrix(c(A[2, 2], -A[1, 2], -A[2, 1], A[1, 1]), 2, 2)
A_inv <- adj_A / det_A
print(A_inv)#输出结果:[,1] [,2]
[1,] -2.0 1.0
[2,] 1.5 -0.5
若要优化这一步骤,很简单,直接用solve():
A <- matrix(c(1, 2, 3, 4), 2, 2)
A_inv <- solve(A)
print(A_inv)
3.5 foreach分解任务
用foreach包实现多线程for循环
library(foreach)
library(doParallel)# 创建一个1000行,1000列的矩阵
m <- matrix(runif(1000000), nrow = 1000)# 初始化并行计算环境
cl <- makeCluster(detectCores())
registerDoParallel(cl)# 使用foreach包和%dopar%运算符进行并行计算
result <- foreach(i = 1:nrow(m), .combine = "+") %dopar% sum(m[i, ])# 结束并行计算环境
stopCluster(cl)# 输出结果
print(result)有人会说,这不就是用了个函数吗?
是,但又不完全是,不然为何有人懂得用这个函数,但有人需要一步一步算(并非说一步一步算不好,只有自己算过,理解了,才懂得去挖掘深度,化繁为简)
4 讨论
如果只知道个函数是知其然而不知其所以然,但是只知道计算过程便如优化前的一样,一步一步计算。得益于现在互联网发展的飞起,各种便利工具各种开源方法,几乎人人都是调包侠,但是当现成的辅佐无法满足时还是需要回归底层。最近深有感触,不论是数据挖掘、还是机器学习深度学习、人工智能、全栈,分析的尽头就是算法。
相关文章:

【R语言】鉴于计算10亿以内训练模型记录for循环的加速
文章目录 1 前言2 几个循环2.1 100以内的和2.2 100以内奇数和/偶数和 3 多重循环3.1 向量化3.2 合并循环3.3 apply函数3.4 矩阵运算3.5 foreach分解任务 4 讨论 1 前言 笔者主力机是MBAM1芯片(8256),某个下午巩固循环突然思考到个问题&#…...
C++类和对象 ——构造函数
C拷贝构造函数详解 什么是拷贝构造函数?拷贝构造函数的特征默认拷贝构造函数为什么需要显示定义构造函数?拷贝构造函数的调用场景什么时候不需要自己定义拷贝构造函数 什么是拷贝构造函数? 在现实生活中,拷贝构造函数就好像我们上…...

第2章-分治法
第2章-分治法 总分:100分 得分:20.0分 1 . 多选题 中等 10分 有关以下代码,说法正确的是( ABCE) def BinarySearch(s, x, low, high):if (low > high):return -1middle (low high) / 2if (x s[mid…...

20天能拿下PMP吗?
新版大纲,专注于人员、过程、业务环境三个领域,内容贯穿价值交付范围(包括预测、敏捷和混合的方法)。除了考试时间由240分钟变更为230分钟、200道单选题变为180道(包含单选和多选)之外,新考纲还…...

Word处理控件Aspose.Words功能演示:在 Java 中将 Word DOC/DOCX 转换为 PDF
Aspose.Words是一种高级Word文档处理API,用于执行各种文档管理和操作任务。API支持生成,修改,转换,呈现和打印文档,而无需在跨平台应用程序中直接使用Microsoft Word。 Aspose API支持流行文件格式处理,并…...

数据安全的重要性
数据安全非常重要,因为我们生活在数字化时代,许多信息和数据都以数字形式存储和传输。如果这些数据受到未经授权的访问、篡改、泄露或破坏,会对个人、组织和国家造成严重的损失。 以下是数据安全的重要性: 1. 保护各类隐私&#x…...
要创建富文本内容?Kendo UI Angular组件有专门的编辑器应对!
您的Angular应用程序可能需要允许用户添加带有格式化选项的文本、图像、表格、外观样式和/或链接,使用Kendo UI for Angular的编辑器,可以轻松搞定这些! Kendo UI for Angular是专业级的Angular UI组件库,不仅是将其他供应商提供…...

工赋开发者社区 | 装备制造企业数字化转型总体框架
导读 当前,面对技术、市场以及供应链等多重挑战,在软件定义、数据驱动、数字孪生、大数据、人工智能及元宇宙等技术加持下,装备制造企业不断采用新工艺、新材料,以新模式推动产品快速创新。企业积极关注并探索数字化转型路径&…...

Python趋势外推预测模型实验完整版
趋势外推预测模型实验完整版 实验目的 通过趋势外推预测模型(佩尔预测模型),掌握预测模型的建立和应用方法,了解趋势外推预测模型(佩尔预测模型)的基本原理 实验内容 趋势外推预测模型 实验步骤和过程…...

KALI入门到高级【第三章】
预计更新第一章 入门 1.1 什么是Kali Linux? 1.2 安装Kali Linux 1.3 Kali Linux桌面环境介绍 1.4 基本命令和工具 第二章 信息收集 1.1 网络扫描 1.2 端口扫描 1.3 漏洞扫描 1.4 社交工程学 第三章 攻击和渗透测试 1.1 密码破解 1.2 暴力破解 1.3 漏洞利用 1.4 特…...

React Native中防止滑动过程中误触
React Native中防止滑动过程中误触 在使用React Native开发的时,当我们快速滑动应用的时候,可能会出现误触,导致我们会点击到页面中的某一些点击事件,误触导致页面元素响应从而进行其他操作,表现出非常不好的用户体验。 一、问题…...
【c语言】函数递归调用
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ…...
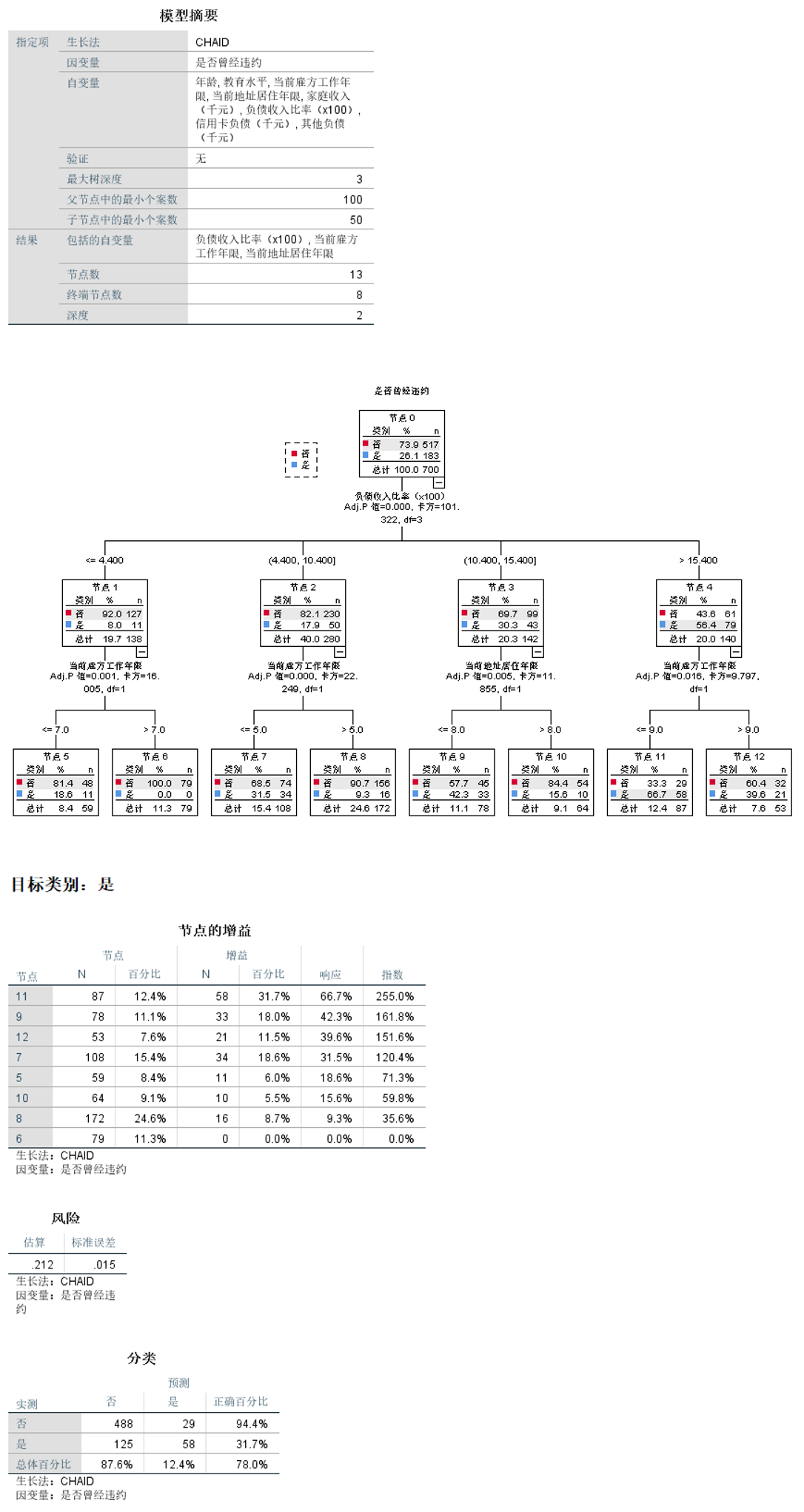
SPSS如何进行判别分析之案例实训?
文章目录 0.引言1.一般判别分析2.逐步判别分析3.决策树分析 0.引言 因科研等多场景需要进行绘图处理,笔者对SPSS进行了学习,本文通过《SPSS统计分析从入门到精通》及其配套素材结合网上相关资料进行学习笔记总结,本文对判别分析进行阐述。 1…...

Windows 10 字体模糊发虚的问题及解决方法
Windows 10字体模糊发虚! 如何解决?Windows 10是一款常见的操作系统,它拥有各种各样的功能,但是有些用户发现,在使用Windows 10时,字体会变得模糊发虚,这给用户带来了很多不便。下面,我们就来看看如何解决…...

渔人杯部分wp
文章目录 渔人杯神仙姐姐阿拉丁飘啊飘 渔人杯 神仙姐姐 点击拜 ,抓包发现get请求了/sx.php 返回如下 {"code":0,"num":1,"flag":"ctfsh0w-f1ag-n0t-h3r3-th1s-msg-just-a-j0ke-}{"}在repeater重复请求,发现…...

测试用例覆盖不全面的解决方法
测试用例覆盖不全面的解决方法 问题分析 在测试用例设计过程中,容易出现思维受限或者需求盲区,我们不可能完全覆盖用户使用的所有场景,编写测试用例的时不可能把所有的场景都能想周全,把所有的场景下的情况都写成测试用例去模拟、…...

AWS Lambda - 第一部分
Hello大家好,我们今天开始讨论AWS Lambda的内容。 SAP认证考试会涉及到很多Lambda的内容,想要通过认证考试虽然不一定非要精通开发,但需要知道Lambda的一些功能和特性、适用场景以及Lambda是如何工作的。 我们开始吧! Lambda与…...

Java 基础进阶篇(七)—— 面向对象三大特征之三:多态
文章目录 一、多态的概述二、多态中成员访问特点 ★三、多态的优势与劣势四、多态下的类型转换4.2 自动类型转换(从子到父)4.2 强制类型转换(从父到子)4.3 instanceof 关键字 一、多态的概述 多态:是指执行同一个行为…...
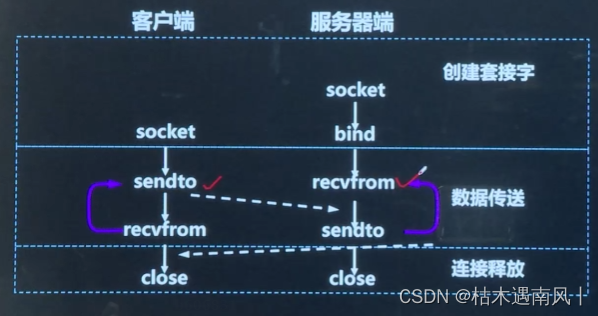
day9 实现UDP通信
目录 socket函数拓展 UDP通信实现过程 代码实现 socket函数拓展 send与recv函数: /*用于发送数据*/ ssize_t send(int sockfd, const void *buf, size_t len,int flags);/*用于接收数据*/ ssize_t recv(int sockfd, void *buf, size_t len,int flags);/*前三个…...
自然语言处理(NLP)在放射学报告评价中的应用:应用和技术进展
自然语言处理(NLP)在放射学报告评价中的应用:应用和技术进展 写在最前面摘要引言先进的技术BERT算法优点 Applications in Radiology 放射学应用Quality 质量将关键发现通知转诊临床医生放射科关键绩效指标和评估 个别放射科医生的表现同行学…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
