校招在线测评题目汇总
图形找规律题
- https://blog.csdn.net/mxj1428295019/article/details/129627461
- https://blog.csdn.net/Yujian2563/article/details/124266574?spm=1001.2101.3001.6650.2&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-124266574-blog-129627461.235%5Ev32%5Epc_relevant_default_base&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-124266574-blog-129627461.235%5Ev32%5Epc_relevant_default_base&utm_relevant_index=3 中外运
- https://www.sohu.com/a/569599673_121058556
- https://zhuanlan.zhihu.com/p/408915596 海康威视笔试题型
- https://blog.csdn.net/wjl31802/article/details/85527885
- https://blog.csdn.net/skyejy/article/details/79606191
- https://blog.csdn.net/u010189239/article/details/89288615
- https://blog.csdn.net/zhanghm1995/article/details/83241814
- https://blog.csdn.net/u010189239/article/details/89298642
- https://blog.csdn.net/u010189239/article/details/89352924
逻辑思维面试题
- https://blog.csdn.net/wjl31802/article/details/85527885
- https://blog.csdn.net/baidu_23959681/article/details/82778995
- https://blog.csdn.net/wcyoot/article/details/7270910
- https://blog.csdn.net/wcyoot/article/details/7273282
- https://blog.csdn.net/wcyoot/article/details/7273463
- https://blog.csdn.net/wcyoot/article/details/7279740
- https://blog.csdn.net/wcyoot/article/details/7279744
- https://blog.csdn.net/wcyoot/article/details/7279746
- https://blog.csdn.net/wcyoot/article/details/7299002
- https://blog.csdn.net/wcyoot/article/details/7299008
数字推理题
- 【招聘测评题】中的（行测）数字推理题基本逻辑总结（附例题）
- 13种行测数字推理技巧总结
- 省考行测大企笔试必备：数字推理题攻略
- 公务员数字推理解题技巧：三角形和圆形
- 行测：数字推理题100道(详解) - 百度文库
- 行测数字推理题常见的数字规律
- 互联网行测笔试题之最头疼的找规律
相关文章：
校招在线测评题目汇总
图形找规律题 https://blog.csdn.net/mxj1428295019/article/details/129627461https://blog.csdn.net/Yujian2563/article/details/124266574?spm1001.2101.3001.6650.2&utm_mediumdistribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-124266574-blo…...
『python爬虫』05. requests模块入门（保姆级图文）
目录 安装requests1. 抓取搜狗搜索内容 requests.get2. 抓取百度翻译数据 requests.post3. 豆瓣电影喜剧榜首爬取4. 关于请求头和关闭request连接总结 欢迎关注 『python爬虫』 专栏，持续更新中 欢迎关注 『python爬虫』 专栏，持续更新中 安装requests …...
WPF超好用的框架Prism入门使用,上位机赶紧学起来!
Prism简介 WPF框架Prism是一种用于开发模块化、可重用和可测试的WPF应用程序的框架。它提供了一种简单而强大的方式来管理复杂应用程序的代码和构建高度可扩展的应用程序。 如何学习Prism框架 如果您想使用Prism框架来开发WPF应用程序，需要学习以下几个方面&…...
十个机器学习应用实例
一、在Kaggle上举办的一个竞赛，名为“Tabular Playground Series - Aug 2021”。该竞赛旨在预测房屋销售价格，数据集包含了79个特征和一个目标变量。参赛者需要训练一个模型，能够预测测试集中房屋的销售价格。 该竞赛的获胜者使用了多个AI模型…...
【Redis17】Redis进阶：管道
Redis进阶：管道 管道是啥？我们做开发的同学们经常会在 Linux 环境中用到管道命令，比如 ps -ef | grep php 。在之前学习 Laravel框架时的 【Laravel6.4】管道过滤器https://mp.weixin.qq.com/s/CK-mcinYpWCIv9CsvUNR7w 这篇文章中，…...
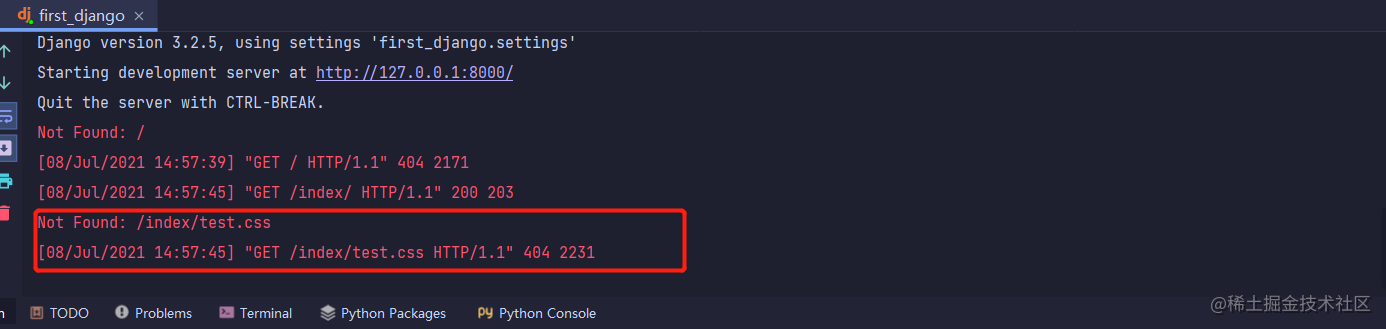
Django项目页面样式如何“传给”客户端浏览器
前言 django项目在视图函数中借助render函数可以返回HTML页面，但是HTML页面中如果引入了外部CSS文件或者JavaScript文件在浏览器页面无法加载，因此就必须有一种方式能够将HTML文档中引入的外部文件能够在客户端浏览器上加载，这种方式就是配置…...
、Pipe()、manager.list()、manager.dict()、manager.Queue())
python 进程间通信 Queue()、Pipe()、manager.list()、manager.dict()、manager.Queue()
👨💻个人简介： 深度学习图像领域工作者 🎉总结链接： 链接中主要是个人工作的总结，每个链接都是一些常用demo，代码直接复制运行即可。包括： &am…...
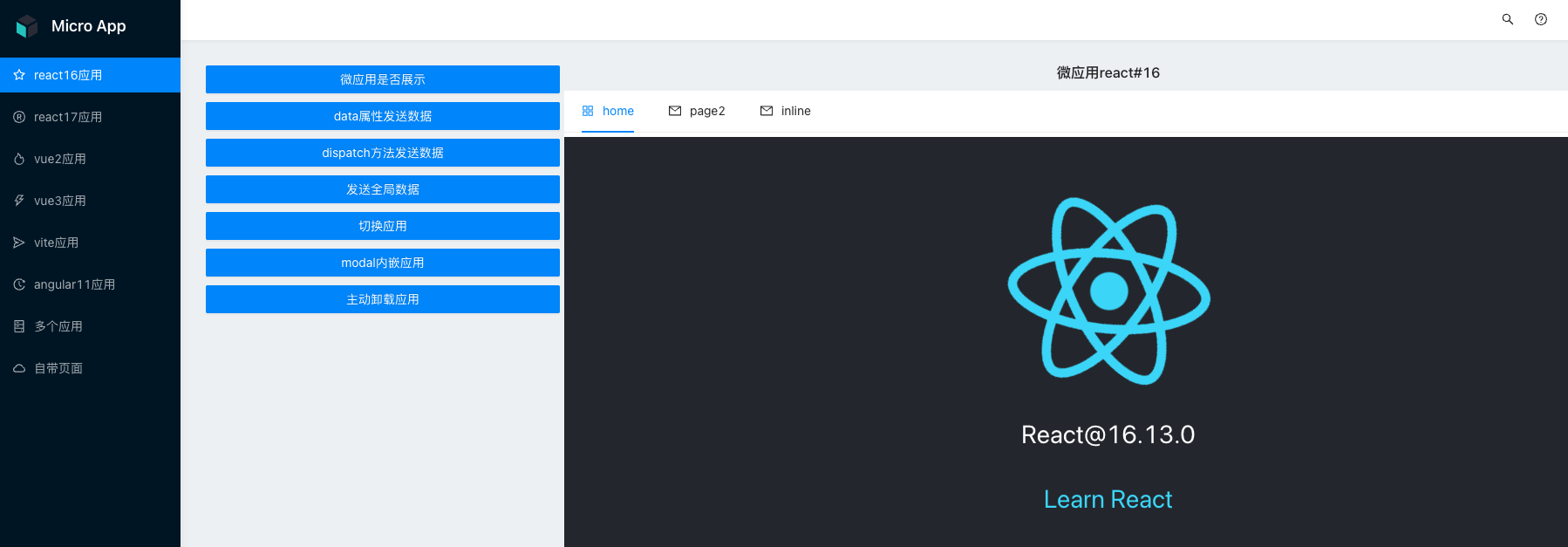
你想要的【微前端】都在这里了！ | 京东云技术团队
作者：京东零售 郑炳懿 开篇： 如果你不知道微前端是什么，或者不知道微前端能解决什么问题，那么你可能不需要微前端。 在我看来，对于每一个没有使用过的新技术，都应该有以下几个过程： 1、调研…...
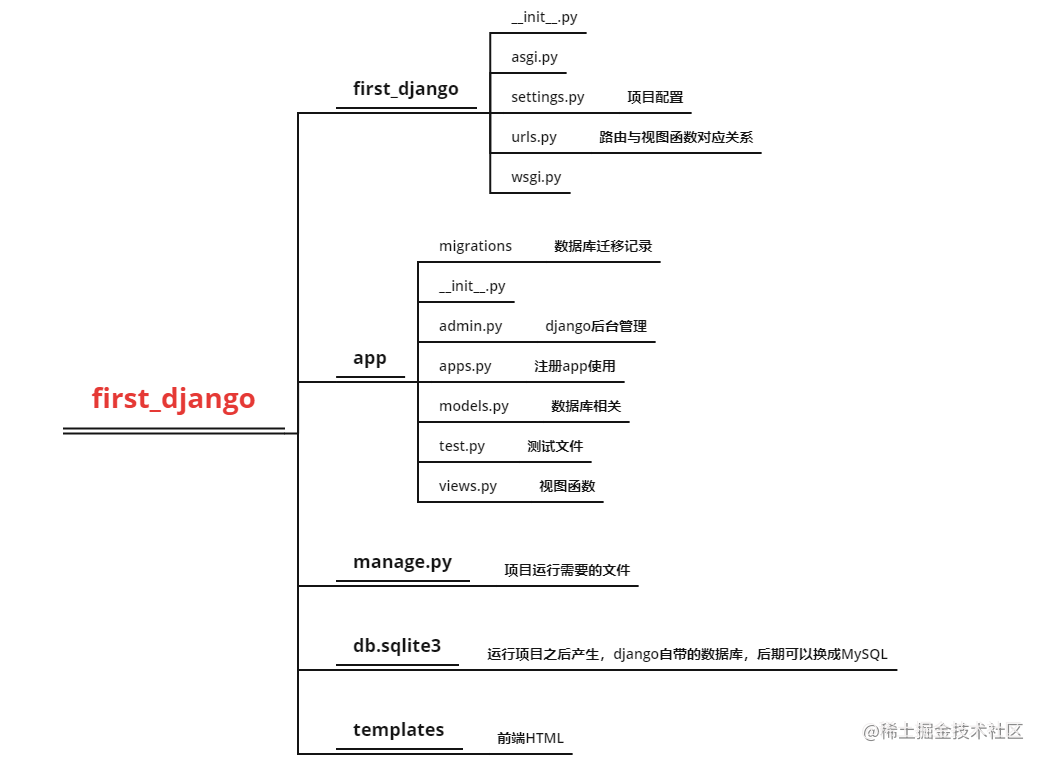
人生若只如初见，你不来看看Django吗
前言 本文介绍python三大主流web框架之一的Django框架的基本使用，如何创建django项目，如何运行django项目以及django项目的目录结构，另外django又是如何返回不同的数据和页面？ python三大主流web框架 Python有三大主流的web框架…...
项目人力资源管理
项目人力资源管理的 4 个过程：规划人力资源管理、组建项目团队、建设项目团队、管理项目团队等内容 单项选择题、案例分析题 人力资源管理领域输入、输出、工具和技术表： 过程名输入工具和技术输出编写项目人力资源计划 项目管理计划活动资源需求事业…...
提供接口给第三方调用，应该注意什么
1.如果我们要提供一个接口给第三方调用，首先我们需要考虑的就是接口安全，一定要做鉴权，至于鉴权的方式：大家可以在网上自行查找，今天我主要记录如何编写一个既能能支持并发的，且不会影响到我们自身业务的的…...
ESL设计概述
前言 随着芯片面临着应用场景丰富多变、集成功能模块越来越多、片内通信及模块间接口越来越复杂、设计规模越来越大以及PPA要求越来越高的需求，芯片设计方法面临越来越大的挑战。架构的合理性、完备性和一致性很大程度上决定了芯片设计的成败。基于同样的I…...
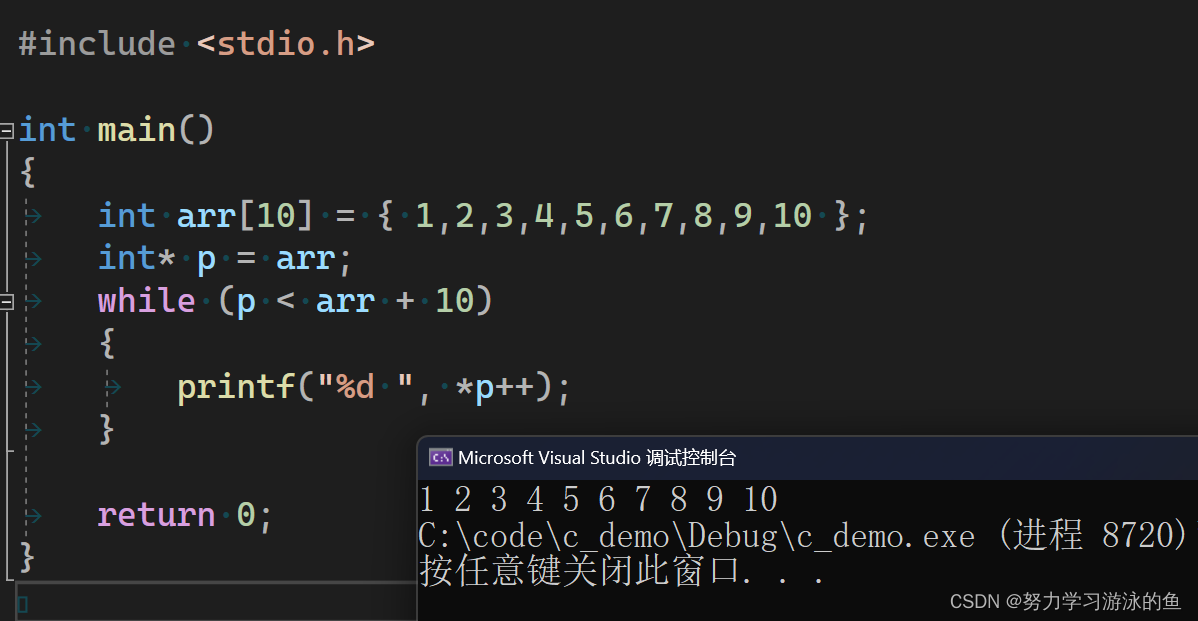
探究C语言数组的奥秘：大小可省略的定义、内存存储、数组名、传参、指针遍历、数组指针和指针数组、柔性数组等
也许你认为，C语言中的数组非常好理解，就是把一组相同类型的元素存储在同一块空间里。但是你可能并没有真正理解数组的本质，不信的话请回答一下下面的几个小问题，如果你能非常清晰的回答这些问题，那么你对C语言中的数组…...
python3 强制使用任意父级相对导入，越过python相对导入限制，拒绝 ImportError
前言 单纯不喜欢 python 对 点开头的包的限制，好麻烦，遂写了本包，来解决这个问题启用本模块后，你可以随时使用 单个点来导入当前目录的模块，也可以使用多个 点导入多级父目录内的模块，而不会报错烦人的模块…...
面了一个4年经验的测试工程师，自动化都不会也要15k，我也是醉了····
在深圳这家金融公司也待了几年，被别人面试过也面试过别人，大大小小的事情也见识不少，今天又是团面的一天， 一百多个人都聚集在一起，因为公司最近在谈项目出来面试就2个人，无奈又被叫到面试房间。 整个过程…...
Java 实现 YoloV7 人体姿态识别
1 OpenCV 环境的准备 这个项目中需要用到 opencv 进行图片的读取与处理操作，因此我们需要先配置一下 opencv 在 java 中运行的配置。 首先前往 opencv 官网下载 opencv-4.6 ：点此下载；下载好后仅选择路径后即可完成安装。 此时将 opencv\b…...
跨越屏幕：桌面PC端的多端开发框架介绍
目前，随着互联网和移动互联网的发展，多端开发框架已经成为越来越多开发者更好的选择。主要有以下几个方面的前景： 跨平台开发需求不断增加：由于不同平台和设备的差异性，开发人员需要使用不同的编程语言和开发工具来为各…...
高效学习方法和工具推荐，让你事半功倍！
本文介绍了五种高效学习方法，包括制定详细的学习计划、集中注意力、不断复习、采用多种学习方式和利用小休息。同时，还推荐了五个高效学习工具和平台，包括Coursera、Duolingo、Quizlet、Khan Academy和Anki，让你在学习中事半功倍&…...
查看Docker容器中RabbitMQ的密码
要查看Docker容器中RabbitMQ的密码，可以尝试以下几个步骤： 1. 查看容器运行时的环境变量 在Docker容器中，可以通过环境变量来设置RabbitMQ的用户名和密码。因此，可以使用以下命令查看容器的环境变量： docker inspect…...
探索Qt线程编程的奥秘：多角度深入剖析
探索Qt线程编程的奥秘：多角度深入剖析 一、Qt线程编程基础（Qt Threading Basics）1.1 线程概念与基本概念（Thread Concepts and Fundamentals）1.2 Qt线程类简介：QThread（Introduction to Qt Thre…...
【杂谈】-递归进化：人工智能的自我改进与监管挑战
递归进化：人工智能的自我改进与监管挑战 文章目录 递归进化：人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管？3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误，它们的含义、原因和解决方法都有显著区别。以下是详细对比： 1. HTTP 406 (Not Acceptable) 含义： 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...
阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能，多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统，涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能，适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
` 方法)
深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出：JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中，随机数的生成看似简单，却隐藏着许多玄机。无论是生成密码、加密密钥，还是创建安全令牌，随机数的质量直接关系到系统的安全性。Jav…...
（二）TensorRT-LLM | 模型导出（v0.20.0rc3）
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述，后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作，其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
零基础设计模式——行为型模式 - 责任链模式
第四部分：行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习！行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想：使多个对象都有机会处…...
c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署，直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型，但是目前国内可能使用不多，至少实践例子很少看见。开发训练模型就不介绍了&am…...
CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构，使它们在 VS 解决方案资源管理器中以“组”（Filter）的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总（共4种） 方法描述是否推荐…...