动态规划问题
目录
一、动态规划简介
二、利用动态规划解决问题
1、斐波拉契序列
2、拆分词句
3、三角形最小路径和
4、不同的路径数目(一)
5、带权值的最小路径和
6、求路径ii
7、01背包
8、不同子序列
9、编辑距离
10、分割回文串
一、动态规划简介
动态规划就是分治思想的延伸,通俗来讲就是大事化小,小事化了。
在将大问题划分为小问题的分治过程中,将小问题的处理结果进行保存以便后面处理大问题时使用到这些结果。
动态规划具有三个特点:
- 将原来的问题分解成几个相似的子问题。
- 所有的子问题只需要解决一次。
- 存储子问题的解。
动态规划的本质:状态的定义和状态方程的定义。
动态规划问题的四个要素:
- 状态的定义。
- 状态间的转移方程的定义。
- 状态的初始化。
- 返回结果。
定义的状态之间要形成递推关系。
动态规划问题的使用场景:求最值、可不可行、是不是、求方案的个数。
二、利用动态规划解决问题
1、斐波拉契序列
题目链接:斐波拉契数列
大家都知道斐波那契数列,现在要求输入一个正整数 n ,请你输出斐波那契数列的第 n 项。
题目分析:
- 状态的定义:F(i) 表示斐波拉契数列的第i项。
- 状态间的转移方程:F(i) = F(i-1)+F(i-2)。
- 初始化:F(1) = 1,F(2) = 1。
- 返回值:F(n)。
代码实现:
public int Fibonacci(int n) {int[] fib = new int[n+1];fib[1] = 1;fib[2] = 1;for(int i = 3;i <= n;i++){fib[i] = fib[i-1] + fib[i-2];}return fib[n];}
2、拆分词句
题目链接:拆分词句
给定一个字符串s和一组单词dict,判断s是否可以用空格分割成一个单词序列,使得单词序列中所有的单词都是dict中的单词(序列可以包含一个或多个单词)。
例如:
给定s=“nowcode”;
dict=["now", "code"].
返回true,因为"nowcode"可以被分割成"now code".
题目分析:
要判断分割的单词序列是否都是dict中的单词,因为分割是从前往后进行分割,那么我们就可以给每个字符设置出一个状态true表示可以分割,如果子状态canSplit[j]为true,也就是前面一部分在dict中,那么判断后面j~i是否为dict中的元素,如果是就将canSplit[i]置为true继续向后判断,由于要判断这个s分割的单词都在dict中,所以就创建canSplit数组时需要增加一个元素canSplit[s.length()]来表示,还有一个特殊情况:如果仅仅分割s的第一个字符为dict中的元素,那么其子问题的状态怎么设定?所以就将canSplit[0]=true,表示0下标之前的状态为true,综上利用动态规划可以分析出:
- 状态的定义 :canSplit[i]:表示该字符对应的下标是否可以拆分
- 状态间转移方程的定义:j<i&&canSplit[i]=true&&dict.contains(subString(j,i))
- 状态初始化:canSplit[0]=true
- 返回结果:canSplit[字符串长度]的状态,表示整个字符串分割的单词是都在dict中。
代码实现:
public boolean wordBreak(String s, Set<String> dict) {if(s == null || dict == null){return false;}boolean[] canSplit = new boolean[s.length()+1];canSplit[0] = true;for(int i = 1;i <= s.length();i++){for(int j = 0;j < i;j++){if(canSplit[j]&&dict.contains(s.substring(j,i))){canSplit[i] = true;}}}return canSplit[s.length()];}3、三角形最小路径和
题目链接:三角形最小路径和
给定一个正三角形数组,自顶到底分别有 1,2,3,4,5...,n 个元素,找出自顶向下的最小路径和。每一步只能移动到下一行的相邻节点上,相邻节点指下行种下标与之相同或下标加一的两个节点。
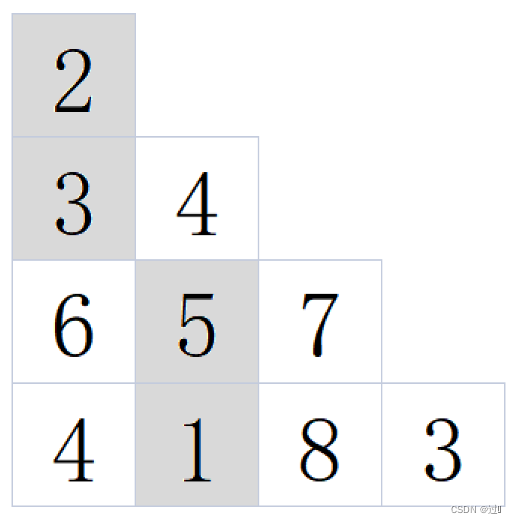
例如当输入[[2],[3,4],[6,5,7],[4,1,8,3]]时,对应的输出为11,
所选的路径如下图所示:
题目分析:
要求从三角形的顶点到底部的最小路径,那么就需要求出其上层的最小路径,假设F(i,j)表示到结点的最小路径,如果该结点是最短路径上的点就直接将该点的值修改为顶点到该点的最小路径和,就不用再开辟新的空间了,又由于每一步只能移动到下一行的相邻节点上,所以结点(i,j)的最短路径F(i,j)=min(F(i-1,j)+F(i-1,j-1)),但是对于三角形两个边上的点其上层的最小路径只需加上其上层的一个点:如果j=0,F(i,j)=F(i-1,j);如果i=j,F(i,j)=F(i-1,j),于是就利用动态规划分析得出:
- 状态的定义:F(i,j):到结点(i,j)的最小路径和(包含结点(i,j)的值)
- 状态间转移方程的定义:F(i,j)=min(F(i-1,j)+F(i-1,j-1)),如果j=0,F(i,j)=F(i-1,j);如果i=j,F(i,j)=F(i-1,j)
- 状态初始化:F(0,0)=val((0,0)结点的值)
- 返回值:min(F(底部结点))
代码实现:
public int minTrace (int[][] triangle) {if(triangle == null){return 0;}int row = triangle.length;for(int i = 1;i < row;i++){for(int j = 0;j <= i;j++){if(j == 0){triangle[i][j] += triangle[i-1][j];}else if( j == i){triangle[i][j] += triangle[i-1][j-1];}else{triangle[i][j] += Math.min(triangle[i-1][j-1],triangle[i-1][j]);}}}int min=triangle[row-1][0];for(int i = 1;i < triangle[row - 1].length;i++){if(triangle[row - 1][i] < min){min = triangle[row -1][i];}}return min;}上述思路是从顶点到点(i,j)的最短路径,那么也可以从点(i.j)到顶点的最短路径,就从倒数第二层开始遍历,那么利用动态规划分析可得:
- 状态的定义:F(i,j) 为底部到点(i,j)的最短路径。
- 状态间转移方程的定义:F(i,j)=min(F(i+1,j)+F(i+1,j+1))。
- 状态初始化:F(i,j)=triangle(i,j)。
- 返回值:F(0,0)。
代码实现:
public int minTrace (int[][] triangle) {if(triangle == null){return 0;}int rows = triangle.length;for(int i = rows - 2;i >= 0;i--){for(int j = 0; j <= i;j++){triangle[i][j] += Math.min(triangle[i+1][j+1],triangle[i+1][j]);}}return triangle[0][0];}4、不同的路径数目(一)
题目链接:不同的路径数目(一)
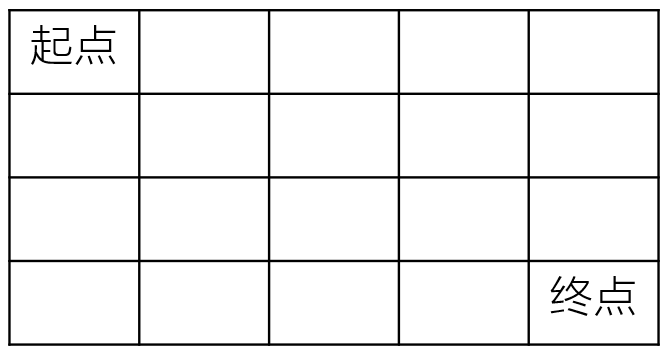
一个机器人在m×n大小的地图的左上角(起点)。
机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。
可以有多少种不同的路径从起点走到终点?
备注:m和n小于等于100,并保证计算结果在int范围内
题目分析:
由于机器人每次可以向下或向右移动,对于到达第一行和第一列的点只有一种路径,经过分析到达其他点的路径方案为左边点的路径方案数和上边点的路径方案数之和。所以利用动态规划分析如下:
- 状态的定义:F(i,j)表示起点到点(i,j)的路径方案数。
- 状态间的转移方程:F(i,j) = F(i-1,j) + F(i,j-1)。
- 状态初始化:F(i,1)=1,F(i,j)=1,到达第一行和第一列的点只有一种路径。
- 返回值:F(m,n)。
代码实现:
public int uniquePaths (int m, int n) {int[][] path = new int[m+1][n+1];for(int i = 1; i <= n;i++){path[1][i] = 1;}for(int i = 1; i <= m;i++){path[i][1] = 1;}for(int i = 2; i <= m;i++){for(int j = 2;j <= n;j++){path[i][j] = path[i][j-1] + path[i-1][j];}}return path[m][n];}5、带权值的最小路径和
题目链接:带权值的最小路径和
给定一个由非负整数填充的m x n的二维数组,现在要从二维数组的左上角走到右下角,请找出路径上的所有数字之和最小的路径。
注意:你每次只能向下或向右移动。
题目分析:
利用动态规划分析如下:
- 状态的定义:F(i,j)表示起点到坐标为(i,j)的最小路径和。
- 状态间的转移方程:F(i,j) = min(F(i-1,j), F(i,j-1))。
- 状态初始化:F(i,0) +=F(i-1,0);F(0,j) +=F(0,j-1)第一行和第一列元素进行初始化。
- 返回值:F(m-1,n-1)。
代码实现:
public int minPathSum (int[][] grid) {int rows = grid.length;int cols = grid[0].length;for(int i = 1; i < rows;i++){grid[i][0] += grid[i-1][0];}for(int i = 1; i < cols;i++){grid[0][i] += grid[0][i-1];}for(int i = 1; i < rows;i++){for(int j =1;j < cols;j++){grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);}}return grid[rows-1][cols-1];}6、求路径ii
题目链接:求路径ii
给定一个m*n的地图,其中加入了一些障碍。每次只能向下或者向右走,问从左上角走到右下角有多少不同的路径?
分别用0和1代表空区域和障碍
例如
下图表示有一个障碍在3*3的图中央。
[[0,0,0],[0,1,0],[0,0,0] ]有2条不同的路径
备注:m和n不超过100.
题目分析:
由动态规划思想分析可得:
- 状态的定义:F(i,j)表示起点到点(i,j)的路径方案数。
- 状态间的转移方程:如果obstacleGrid(i,j)=1,F(i,j)=0,否则F(i,j)=F(i-1,j)(j=0),F(i,j)=F(i,j-1)(i=0),F(i,j) = F(i-1,j) + F(i,j-1)(i!=0,j!=0)。
- 状态初始化:F(0,0)=obstacleGrid(0,0)==1?0:1。
- 返回值:F(m-1,n-1)。
代码实现:
public static int uniquePathsWithObstacles (int[][] obstacleGrid) {if(obstacleGrid==null)return 0;int i,j;int m=obstacleGrid.length;int n=obstacleGrid[0].length;int[][]f=new int[m][n];if(obstacleGrid[0][0]==1){return 0;}else{f[0][0]=1;}for(i=0;i<m;i++){for(j=0;j<n;j++){if(obstacleGrid[i][j]==1){f[i][j]=0;continue;}if(i==0&&j!=0){f[i][j]=f[i][j-1];}if(i!=0&&j==0){f[i][j]=f[i-1][j];}if(i!=0&&j!=0){f[i][j]=f[i-1][j]+f[i][j-1];}}}return f[m-1][n-1];}7、01背包
题目链接:01背包
已知一个背包最多能容纳体积之和为v的物品,现有 n 个物品,第 i 个物品的体积为 vi , 重量为 wi,求当前背包最多能装多大重量的物品?
题目分析:
- 状态的定义:F(i,j)表示i个物品和体积为j的重量。
- 状态间的转换方程: 如果空间不足,F(i,j) = F(i-1,j).如果空间充足就要判断是否放入元素取max( F(i-1,j),(F(i-1,j-vi)+wi))。
- 初始化:第0行和第0列的元素为0,表示未放任何物品和体积为0的情况。
- 返回值:F(m,n)。
代码实现:
/*** 计算01背包问题的结果* @param V int整型 背包的体积* @param n int整型 物品的个数* @param vw int整型二维数组 第一维度为n,第二维度为2的二维数组,vw[i][0],vw[i][1]分别描述i+1个物品的vi,wi* @return int整型*/
public static int knapsack (int V, int n, int[][] vw) {int[][] maxValue = new int[n+1][V+1];for(int i = 1; i <= n;i++){for(int j = 1; j <= V;j++){if(j < vw[i-1][0]){maxValue[i][j] = maxValue[i-1][j];}else{maxValue[i][j] = Math.max(maxValue[i-1][j],maxValue[i-1][j-vw[i-1][0]]+vw[i-1][1]);}}}return maxValue[n][V];
}8、不同子序列
题目链接:不同的子序列
给定两个字符串S和T,返回S子序列等于T的不同子序列个数有多少个?
字符串的子序列是由原来的字符串删除一些字符(也可以不删除)在不改变相对位置的情况下的剩余字符(例如,"ACE"is a subsequence of"ABCDE"但是"AEC"不是)
例如:S="nowcccoder", T = "nowccoder"
返回3
题目分析:
- 状态的定义:dp[i][j]表示以i-1结尾的字符串S等于以j-1结尾的字符串T子序列的个数。
- 状态间的转移方程:dp[i][j]=(S[i-1]==T[j-1])?(dp[i-1][j-1]+dp[i-1][j]):dp[i-1][j].
- 初始化:dp[0][j] = 0,表示S字符串为空,dp[i][0] = 1,表示T字符串为空,dp[0][0]=1表示S和T都为空。
- 返回值:dp[S.length()][T.length()]。
代码实现:
public int numDistinct (String S, String T) {int lenS = S.length();int lenT = T.length();int[][] dp = new int[lenS+1][lenT+1];for(int i = 0;i <= lenS;i++){dp[i][0] = 1;}for(int i = 1;i <= lenS;i++){for(int j = 1;j <= lenT;j++){if(S.charAt(i-1) == T.charAt(j-1)){dp[i][j] = dp[i-1][j-1] + dp[i-1][j];}else{dp[i][j] = dp[i-1][j];}}}return dp[lenS][lenT];}9、编辑距离
题目链接:编辑距离
给定两个单词word1和word2,请计算将word1转换为word2至少需要多少步操作。
你可以对一个单词执行以下3种操作:
a)在单词中插入一个字符
b)删除单词中的一个字符
c)替换单词中的一个字符
题目分析:
- 状态的定义:dp[i][j]表示前i-1的word1转换为前j-1的word2需要多少步操作。
- 状态间的转换方程:dp[i][j]=(word1[i-1]==word2[j-1])?dp[i-1][j-1]:(min(dp[i-1][j]+1, dp[i][j-1]+1,dp[i-1][j-1]+1),dp[i-1][j]+1表示删除word1的第i-1个字符,dp[i][j-1]+1表示新增word1的第i-1个字符,dp[i-1][j-1]+1表示替换word1的第i-1个字符。
- 初始化:dp[0][0] = 0,dp[0][j] = j,dp[i][0] = i。
- 返回值:p[word1.length()][word2.length()]。
代码实现:
public int minDistance (String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1+1][len2+1];for(int i = 1;i <= len1;i++){dp[i][0] = i;}for(int j = 1;j <= len2;j++){dp[0][j] = j;}for(int i = 1;i <= len1;i++){for(int j = 1;j <= len2;j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1];}else{int min1 = Math.min(dp[i-1][j-1],dp[i-1][j]);int min2 = Math.min(dp[i][j-1],dp[i-1][j]);dp[i][j] = Math.min(min1,min2) + 1;}}}return dp[len1][len2];}10、分割回文串
题目链接:分割回文串
给出一个字符串s,分割s使得分割出的每一个子串都是回文串
计算将字符串s分割成回文分割结果的最小切割数
例如:给定字符串s="aab",
返回1,因为回文分割结果["aa","b"]是切割一次生成的。
题目分析:
- 状态的定义:dp[i]表示到第i个字符分割的次数。
- 状态间的转移方程:dp[i] = min(dp[i],dp[j]+1)。
- 初始化:dp[i]表示到第i个字符的最大分割次数。
- 返回值:dp[s.length()]。
public boolean isPalindrome(String s){int begin = 0;int end = s.length()-1;while(begin < end){if(s.charAt(begin) == s.charAt(end)){begin++;end--;}else{return false;}}return true;}public int minCut (String s) {int len = s.length();int[] dp = new int[len+1];for(int i = 0;i <= len;i++){dp[i] = i-1;}for(int i = 1;i <= len;i++){for(int j = 0;j<i;j++){if(isPalindrome(s.substring(j,i))){dp[i] = Math.min(dp[i],dp[j]+1);}}}return dp[len];}相关文章:
动态规划问题
目录 一、动态规划简介 二、利用动态规划解决问题 1、斐波拉契序列 2、拆分词句 3、三角形最小路径和 4、不同的路径数目(一) 5、带权值的最小路径和 6、求路径ii 7、01背包 8、不同子序列 9、编辑距离 10、分割回文串 一、动态规划…...

【MySQL进阶】 存储引擎 索引
😊😊作者简介😊😊 : 大家好,我是南瓜籽,一个在校大二学生,我将会持续分享Java相关知识。 🎉🎉个人主页🎉🎉 : 南瓜籽的主页…...
5 款最好的免费 SSD 数据恢复软件
SSD(固态硬盘)提供比传统硬盘更快的读/写速度,使启动、软件加载和游戏启动更快。因此,在我们选择存储设备时,它是一个极好的选择。但是,它仍然存在数据丢失的风险。假设您是受害者之一,正在寻找…...
MyBatis案例 | 使用映射配置文件实现CRUD操作——删除数据
本专栏主要是记录学习完JavaSE后学习JavaWeb部分的一些知识点总结以及遇到的一些问题等,如果刚开始学习Java的小伙伴可以点击下方连接查看专栏 本专栏地址:🔥JavaWeb Java入门篇: 🔥Java基础学习篇 Java进阶学习篇&…...

CSDN 编程竞赛二十八期题解
竞赛总览 CSDN 编程竞赛二十八期:比赛详情 (csdn.net) 本期竞赛的题目都很简单,但是非常考验读题和编码速度。这一次没有遇到bug,竞赛体验较好。 竞赛题解 题目1、小Q的鲜榨柠檬汁 团建活动是大家所想要的。小Q给大家准备了鲜橙汁。现在…...

DML数据操纵语言
DML数据操纵语言 目录概述一、插入语句(一)方式一(二)方式二:(三)两种方式的比较二、修改语句三、删除语句概述方式一:delete方式二:truncate语句 【清空语句】delete VS truncate 【面试题!!!】概述 数据…...
【Hello Linux】Linux工具介绍 (gcc/g++ gdb)
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:介绍Linux的常用工具gcc/g 以及gbd Linux工具介绍gcc / ggcc / g的作用为什么语言要经过这四步才能变为可执行指令gcc / g语法预处理编…...

TeamFiltration:一款针对O365 AAD账号安全的测试框架
关于TeamFiltration TeamFiltration是一款针对O365 AAD账号安全的跨平台安全测试框架,在该工具的帮助下,广大研究人员可以轻松对O365 AAD账号进行枚举、喷射、过滤和后门植入等操作。TeamFiltering与CrackMapExec非常相似,它可以创建并维护一…...

你是真的“C”——Visual Studio 2022(VS2022)编译器 -—实用调试技巧
你是真的“C”——Visual Studio 2022(VS2022)编译器 -—实用调试技巧😎前言🙌1. 什么是bug?🙌2. 调试是什么?有多重要?🙌2.1 调试是什么?2.2 调试的基本步骤…...
数据结构与算法:7种必须会的排序以及3种非基于比较排序
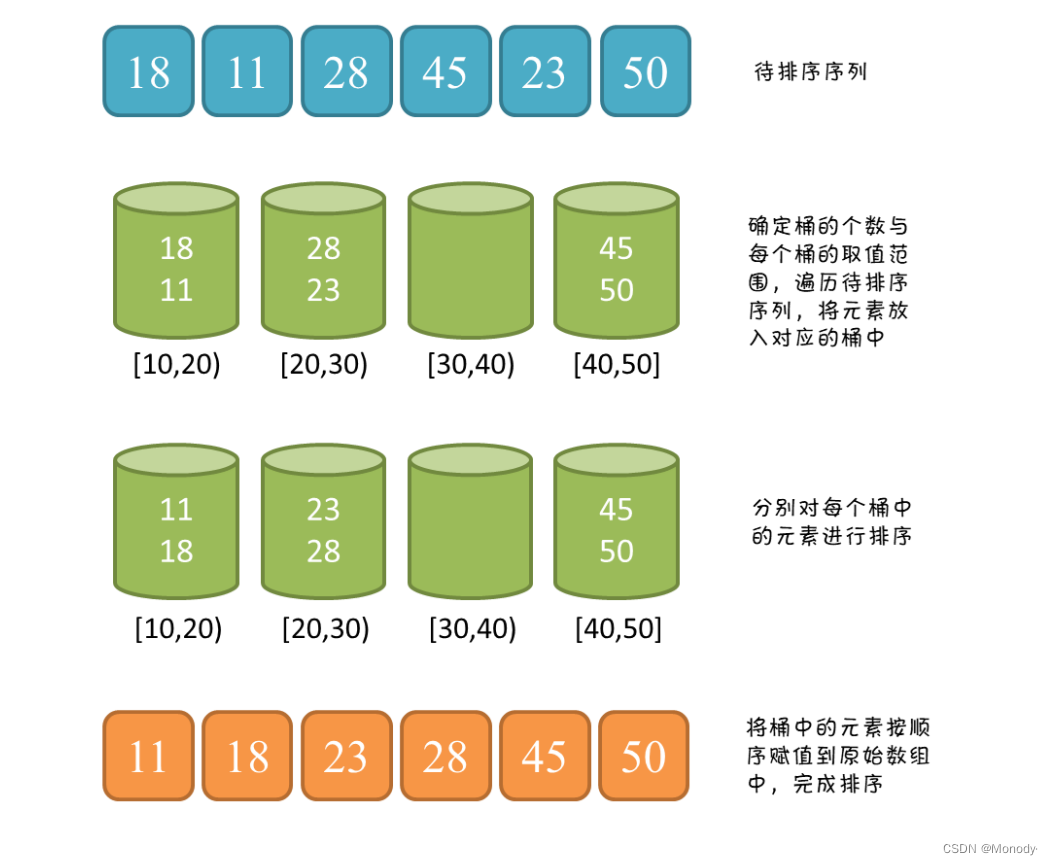
1.什么是排序 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序…...

数据库用户数
Oracle的用户数 oracle软件内部并没对用户数做限制,买5个用户数,指你买了5个user licences,从法律上只能连5个session,超过5个的连接都是非法的。oracle不给你技术上的限制,可是给你法律上的限制。 一般来讲…...

nginx如何用html显示多个图片并加入播放链接
需求背景通过nginx来做个点播服务,ffmpeg截取视频中的某一帧作为视频的封面,前端页面展示这个封面,,并链接到对应的视频播放链接,加载播放器进行播放简单介绍一下ffmpeg截取视频中的某一帧的方式截取视频的第一帧&…...

【蓝桥杯集训·每日一题】Acwing 3729. 改变数组元素
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一维差分区间合并一、题目 1、原题链接 3729. 改变数组元素 2、题目描述 给定一个空数组 V 和一个整数数组 a1,a2,…,an。 现在要对数组 V 进行 n 次操作。 第 i 次操作的…...
springmvc执行流程
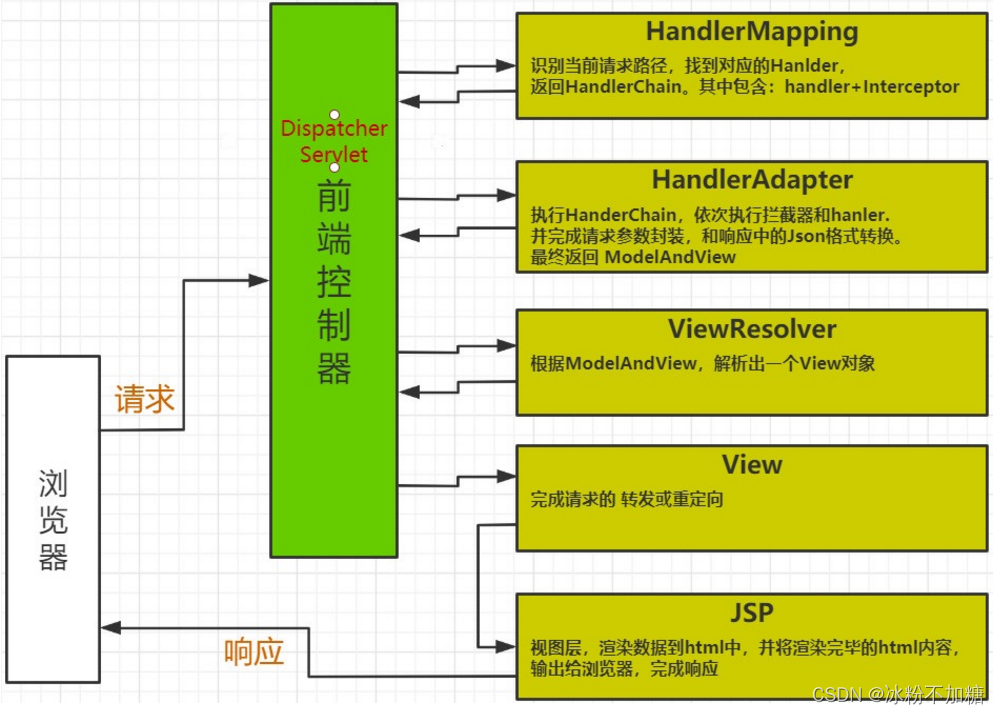
文章目录前言一、springMVC请求执行流程二、组件说明以下组件通常使用框架提供实现:总结前言 本篇文章是对springmvc的补充 接上篇文章springmvc入门https://blog.csdn.net/l_zl2021/article/details/127120873 一、springMVC请求执行流程 1.用户发送请求至前端控制…...
SpringMVC(2)
一)接受到JSON格式的数据:使用RequestBody来进行接收 ResponseBody表示的是返回一个非页面的数据 RequestBody表示的是后端要接受JSON格式的数据 一)接收单个格式的JSON格式的数据,我们使用一个对象来进行接收 1)我们之前接受GET请求中的queryString中的参数的时候&…...

Jackson序列化json时null转成空串或空对象
在项目中可能会遇到需要将null转"",可以通过以下方法解决。一:添加JacksonConfig 配置import com.fasterxml.jackson.core.JsonGenerator;import com.fasterxml.jackson.databind.JsonSerializer;import com.fasterxml.jackson.databind.Objec…...

如何将Python的上级目录的文件导入?【from.import】
假如有如下目录: -python ----file1 ---------file1_1 ------------------pfile1_1.py ---------pfile1.py ----file2 ---------pfile2.py ----pfile.py ----data.py 在pfile1_1.py中想要将pfile.py 导入怎么办? 首先将其上级目录添加到系统目…...

Java实现碧蓝航线连续作战
目录一.实现功能二.主要思路三.代码实现四.用exe4j生成.exe程序五.最终效果六.代码开源一.实现功能 主线图作战结束到结算页自动点击再次前往 二.主要思路 判断是否进入了结算界面:记录结算界面某个像素点的RGB值,每隔3秒对这个像素点进行比对 移动鼠标…...
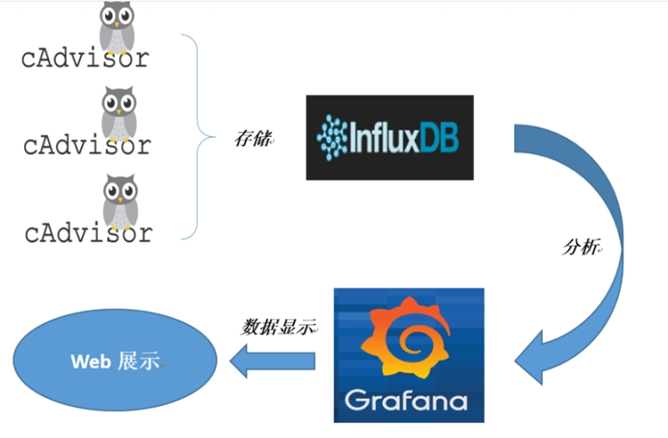
Docker笔记
文章目录1.docker为什么会出现2.docker是什么3.传统虚拟机和容器的对比3.1虚拟机3.2容器虚拟化技术3.3两者对比3.4为什么Docker会比VM虚拟机快?4.docker能干嘛6.docker的应用场景7.docker三要素一:镜像(Image)二:容器&…...
情人节使用AI TOOL来创建一个甜言蜜语的女伴
一、首先使用chatgpt生成一段情侣间的对话,需要反复几次,达到满意的程度,然后将女方的话归在一起。 这是一个情侣私下谈话的场景,女方表示对男朋友精心准备的情人节安排和礼物表示很满意 二、 打开网站:https://lexic…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...