Codeforces Round 867 (Div 3) 总结
文章目录
- A
- B
- C
- D
- E
文章首发于我的个人博客:欢迎大佬们来逛逛
Dashboard - Codeforces Round 867 (Div. 3) - Codeforces
A
题目大意:有n个电视节目,每个电视节目占据一定的时间,并且具有一个娱乐值,一秒可以额换一次台,你需要在规定的时间内找出最大娱乐值的电视节目。(一个电视节目必须看完,意味着你的剩余时间必须大于这个电视节目的时间)
我们可以将自己的规定时间与电视节目进行枚举,相当于每次进行一次换台,如果我们的剩余时间大于电视节目所占据的时间,则每次记录一下娱乐值的最大值。
B
题目大意:给出一个序列,你可以任意删除其中的元素,规定序列中的最美值为序列中相邻两个元素的乘积的最大值,找出整个序列中的最美值。
由于可以删除元素,则我们就可以认为元素之间是无序的,因此我们可以进行排序,从小到大,然后进行遍历相邻两元素乘积最大值即可。
C
题目大意:在一个 n*n 的图形中,找出整个图形(包括内部和外部)的线的总长,每一段线长 1。
这是一道规律题:
- n=4:容易得到 15 + 3 + 2*4 为 26
- n=5:容易得到 24 + 3 + 2*5 为 37
- n=6:容易得到 35 + 3 + 2*6 为 50
因此公式为:
a n s = n ∗ n − 1 + 3 + 2 ∗ n ans = n*n-1 + 3 + 2*n ans=n∗n−1+3+2∗n
D
题目大意:寻找超级排列,所谓超级排列是指从 1到n 每个元素只出现一次,不能不出现,也不能重复出现。规定 b数组为 a数组的前缀和数组%n,如果 b数组为超级排列,那么a数组也是超级排列。因此给你一个 n,判断这个n能否构成一个超级排列。
- 如果n是奇数,那么n的前缀和数组的最后一项一定是 n的倍数,同理 n-1项也一定是n的倍数
- 例如:n=5: s = 1 3 6 10 15;则 10与15都是n的倍数,因此%n都为0,所以不是超级排列
- n=1除外
- 如果n是偶数,则不妨找规律:
- n=6: 6 5 2 3 4 1,可以看作 n n-1 (n-1)。其中前两项是固定的,往后每两项都需要组成一个 n-1 ,因此 2+3 =5;4+1 =5,可以算出这样的排列一定是超级排列。
- 第三项开始枚举 2 4 6 …. 对应为 n-1-2 n-1-4 n-1-6
E
题目大意:一个字符串,你可以交换任意两个位置元素,使得这个字符串每一个字符位置都不回文,即s[i] ≠ s[n-i-1] (i≥0) ,求出是否可以经过操作得到,输出交换次数,否则输出 -1
- 无解:
- 观察到奇数个数得字符一定是无解的,因为会多一个字符无法匹配。
- 如果一个字符出现次数大于数组总长度的一半,则一定会出现一半全是这个字符,另一半至少出现一个这个字符,因此一定有重复,无解。
- 有解:
- 左半边记录不满足条件时的该元素出现的次数,相邻两个元素可以进行一次交换,因此抵消为一次,直到记录的不满足条件的元素的次数为0,使用multiset维护很方便!
相关文章:
 总结)
Codeforces Round 867 (Div 3) 总结
文章目录 ABCDE 文章首发于我的个人博客:欢迎大佬们来逛逛 Dashboard - Codeforces Round 867 (Div. 3) - Codeforces A 题目大意:有n个电视节目,每个电视节目占据一定的时间,并且具有一个娱乐值,一秒可以额换一次台…...

vue修饰符的使用
事件修饰符: 在处理事件时调用 event.preventDefault() 或 event.stopPropagation() 是很常见的。尽管我们可以直接在方法内调用,但如果方法能更专注于数据逻辑而不用去处理 DOM 事件的细节会更好。 为解决这一问题,Vue 为 v-on 提供了事件…...
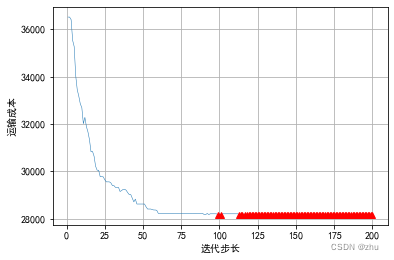
2023年五一数学建模 B 题过程与结果
文章目录 第一问第二问数据时序分析Auto-ARIMA第二问求解解的情况A->Q:D-> AQ-V总快递数 第三问第四问遗传算法求解 第五问SARIMA 模型拟合季节性规律 第一问 见 2023 年 五一杯 B 题过程 代码(第一问) 第二问 第二问考虑是一个时序预测问题&a…...
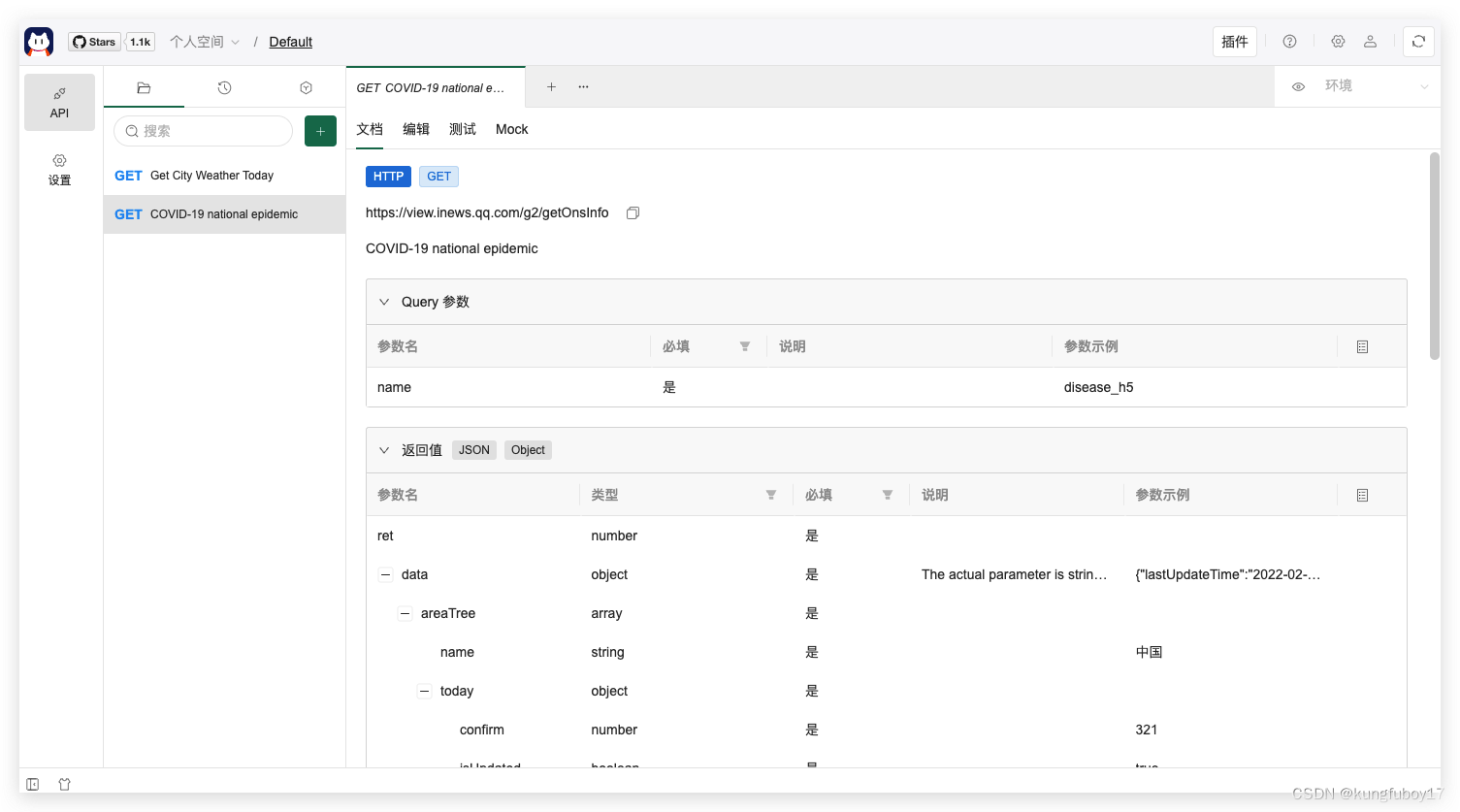
搞懂 API ,API 中 URI 设计规范分享
API(Application Programming Interface)是现代软件开发中的一项关键技术,它为不同应用程序间提供了数据和功能交互的标准化方式。而 URI(Uniform Resource Identifier)作为 API 中的重要部分,其规范和良好…...
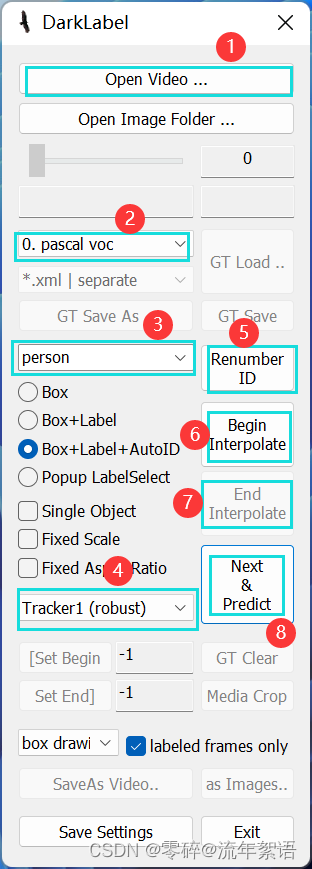
【DarkLabel】使用教程(标注MOT数据集)
DarkLabel 使用教程 功能部分 Open video 第 2 处的内容为数据集类型。例如:VOC、COCO、MOT、YOLO等。 第 3 处的内容为标签名称。 可在 darklabel.yml 中修改 classes_set。例如:classes_set: "mot_classes" 第 4 处的内容为两种跟踪方法…...

Python3 迭代器与生成器
Python3 中的迭代器和生成器是 Python 编程中非常重要的概念,它们可以帮助我们更高效地处理数据和管理内存。下面分别介绍一下迭代器和生成器的概念和用法。 ## 迭代器 迭代器是一个可以遍历一个容器(如列表或元组)中的所有元素的对象&…...
C++基础 类的自动转换和强制类型转换
参考 C Primer Plus (第6版) 类自动转换 接受一个参数的构造函数允许使用赋值语法将对象初始化一个值 Classname object value; 等价于 ClassName object(value); 等价于 ClassName object ClassName(value); 只有接受一个参数的构造函数才能作为转换构造函数(某类型->…...
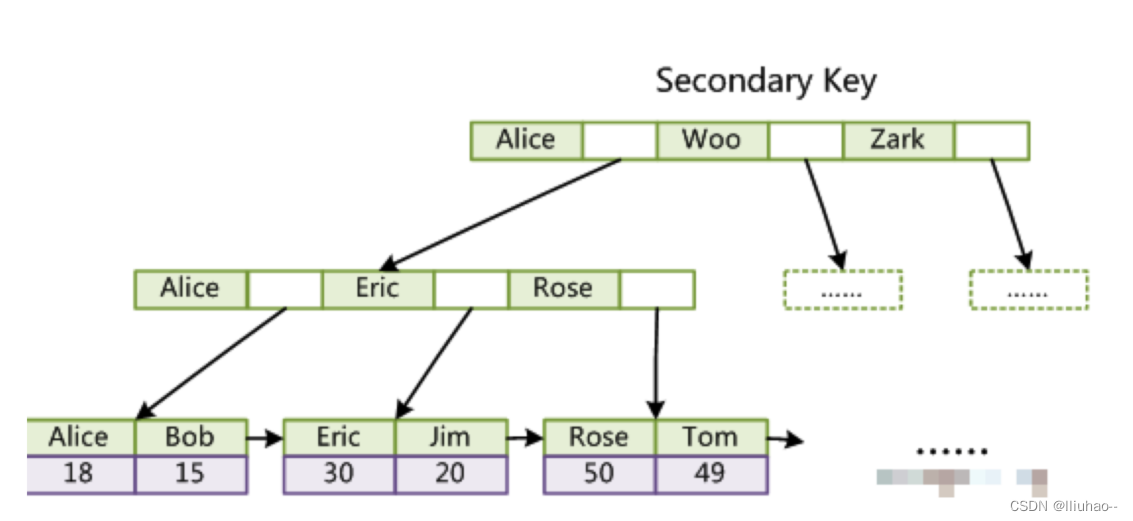
MySQL索引的底层实现原理
索引的底层实现原理 数据库索引是存储在磁盘上的,当数据量大时,就不能把整个索引全部加载到内存了,只能逐一加载每一个磁盘块(对应索引树的节点),索引树越低,越“矮胖”,磁盘IO次数…...

Linux 更新
Linux权限系统 01 只读 1 10 只写 2 100 只执行 4 11 可读写 3 101 可读执行 5 110 可写执行 6 111 可读写执行 7...
)
华为OD机试 - 端口合并(Python)
题目描述 有M个端口组(1<=M<=10), 每个端口组是长度为N的整数数组(1<=N<=100), 如果端口组间存在2个及以上不同端口相同,则认为这2个端口组互相关联,可以合并。 输入描述 第一行输入端口组个数M,再输入M行,每行逗号分割,代表端口组。 备注:端口组内数字…...

分部积分法习题
前置知识:分部积分法 例题 计算积分 I n ∫ [ ( x a ) 2 b 2 ] − k d x ( n ≥ 1 ) I_n\int [(xa)^2b^2]^{-k}dx \quad(n\geq 1) In∫[(xa)2b2]−kdx(n≥1) 解: \qquad 用分部积分法,对任何自然数 k ≥ 1 k\geq 1 k≥1,…...
C++—非递归【循环】遍历二叉树(前序,中序,后序)思路讲解+代码实现
非递归遍历二叉树 前序中序后序 接下来我们在研究如何使用循环实现遍历二叉树时,以下面的二叉树为例: 在下文的讲解中,不对如何构建这颗二叉树做讲解,直接给出代码,如果有不懂的地方欢迎私信我。 文章中的完整源代码链…...
前端002_初始化项目
1、命名和启动项目 将目录名 vue-admin-template-master 重命名为 db-manager-system 将 db-manager-system/package.json 中的 name 值改为 db-manager-system {"name": "db-manager-system","version": "1.0.1","descriptio…...

组合设计模式
组合模式 组合模式定义使用场景1、文件系统的目录结构:2、组织架构图:3、菜单和菜单项:4、使用场景总结: 角色定义Component 抽象构件角色:Leaf 叶子构件:Composite 树枝构件: 需求背景代码实现Component(抽象构件角色…...
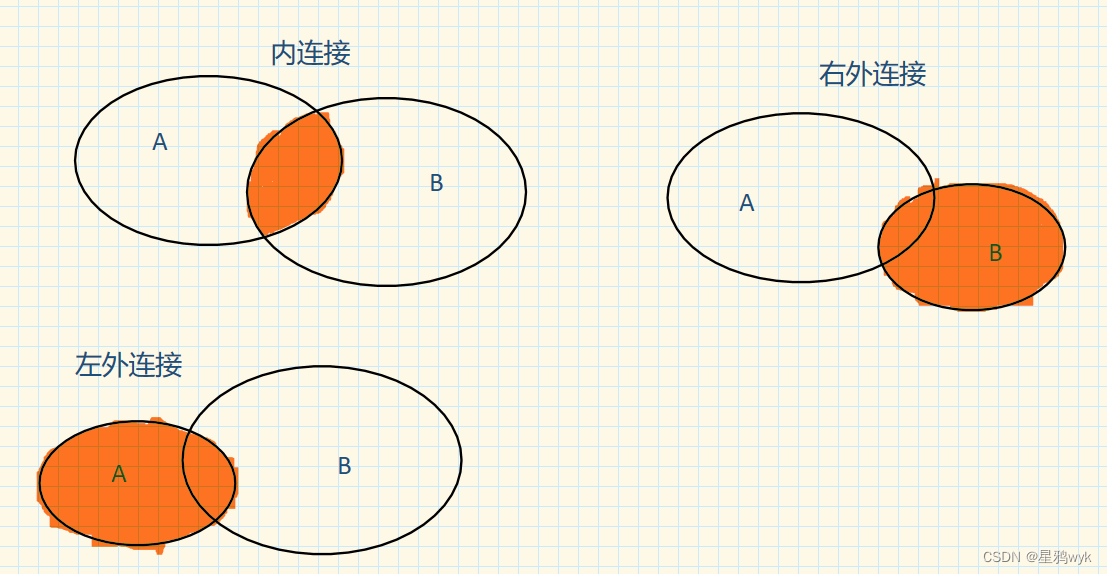
【MySQL】多表查询
上一篇介绍了外键约束,外键约束是用于连接两张数据表的,所以在此基础上就有了多表查询 之前的查询都是单表查询,这里我们会将多个数据表的数据结果返回在一张表上 文章目录 1.多表关系2.多表查询2.1 多表查询分类2.2 内连接2.3 外连接2.4 自连接2.5 联合查询2.6子查询 1.多表关…...

关于在线帮助中心你需要思考以下几个问题
搭建帮助中心是大多数企业都在尝试做的事情,它的重要性对于企业来说不言而喻。现在对于企业来说,搭建帮助中心或许不是什么难事,但是关于帮助中心,有几个问题需要思考清楚,才能让其发挥最大的价值。 一、如何让用户养成…...
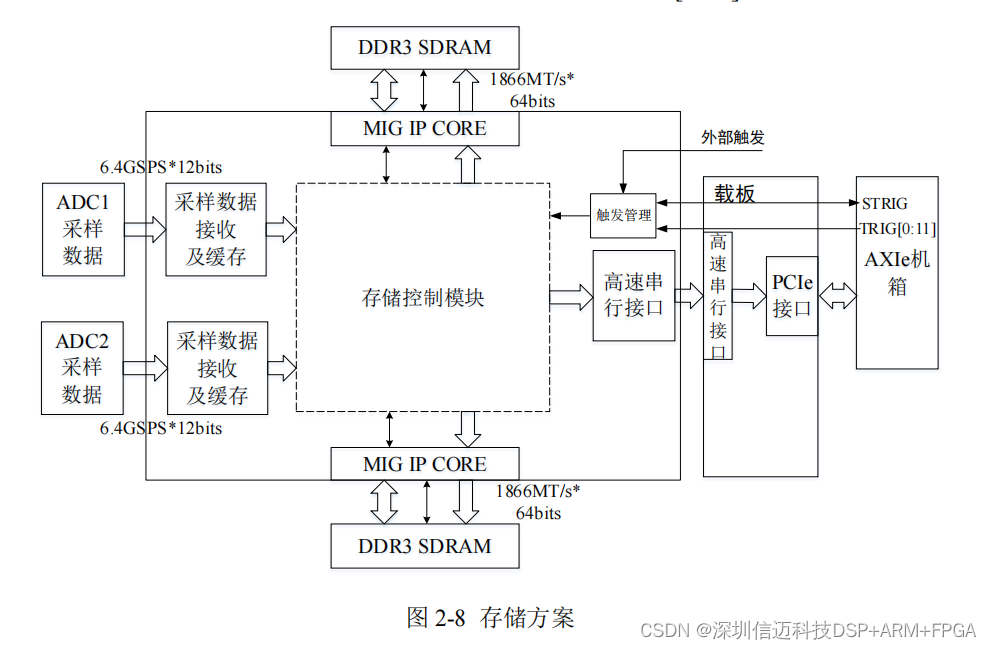
基于FPGA+JESD204B 时钟双通道 6.4GSPS 高速数据采集模块设计(一)总体方案
本章将根据高速数据采集指标要求,分析并确定高速数据采集模块的设计方 案,由此分析数据存储需求及存储速度需求给出高速大容量数据存储方案,完成 双通道高速数据采集模块总体设计方案,并综合采集、存储方案及 AXIe 接口需求 …...
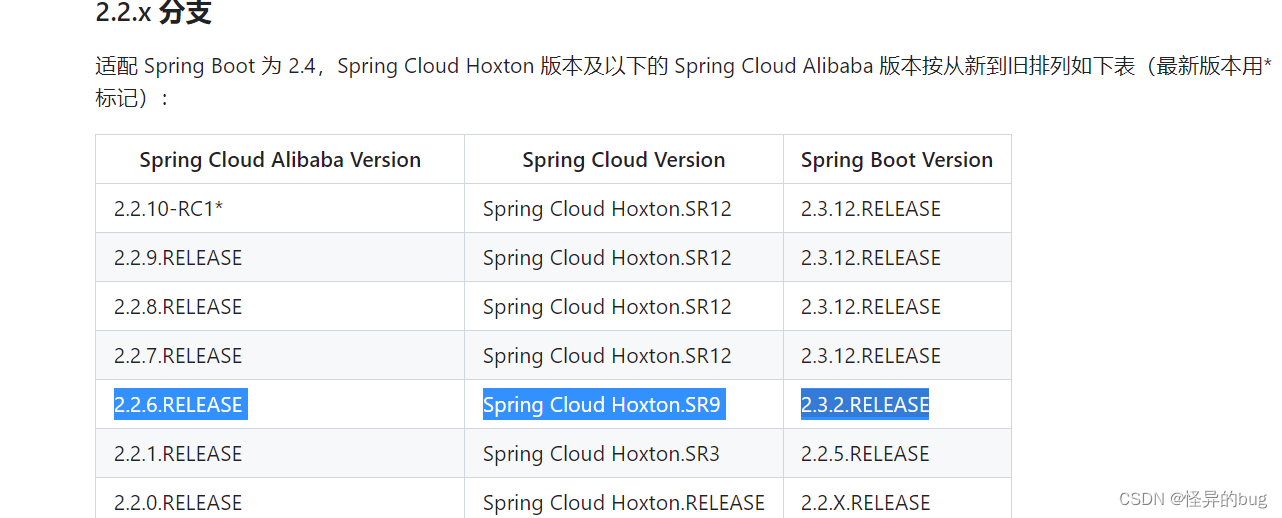
二、Spring Cloud Alibaba环境搭建
一、依赖环境 SpringCloud Alibaba 依赖 Java 环境来运行。还需要为此配置 Maven环境,请确保是在以下版本环境中安装使用。 64 bit JDK 1.8;Maven 3.2.x。 spring-cloud-alibaba相关网址: 地址:https://github.com/alibaba/spring-cloud-…...
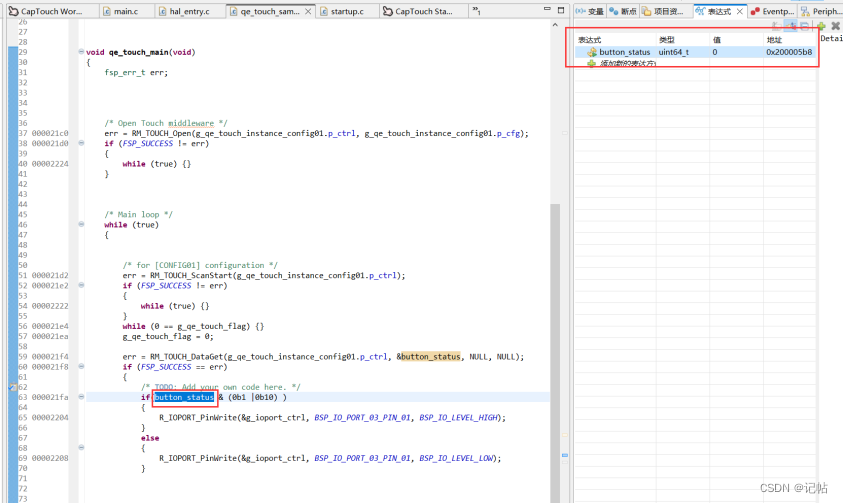
瑞萨e2studio(24)----电容触摸配置(1)
瑞萨e2studio.24--电容触摸配置1 概述硬件准备新建工程工程模板保存工程路径芯片配置工程模板选择时钟配置添加TOUCH驱动配置CapTouch开启调优界面启动 CapTouch 调优通过电容触摸点亮LED 概述 这篇文档将创建一个使用 e2 studio 集成 QE 的电容式触摸应用示例,通…...
数据开发常见问题
目录 环境变量过多或者参数值过长时,为什么提交作业失败? 为什么Shell作业状态和相关的YARN Application状态不一致? 创建作业和执行计划的区别是什么? 如何查看作业运行记录? 如何在OSS上查看日志? 读…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
