智慧城市规划数字化管理:数字孪生技术的创新应用
随着智能城市的不断发展,数字孪生技术也开始在智慧城市的建设中得到了广泛应用。数字孪生作为一种数字化的复制技术,它可以模拟真实世界中的实体和过程。

在城市规划方面,数字孪生可以帮助城市规划师更加直观地了解城市的整体规划和发展趋势,同时也可以预测出城市未来的需求和变化。在交通管理方面,数字孪生可以帮助城市管理者更好地规划城市交通系统,提高交通效率,减少拥堵和交通事故。在公共安全方面,数字孪生可以帮助城市管理者更好地掌握城市公共安全状况,及时发现和解决各种安全问题。
在数字孪生技术应用于智慧城市建设中,图扑(Hightopo)所实现的城市规划数字化管理是其中的一项重要应用。通过数字化城市的各项数据,包括建筑物、道路、公共设施等,实现了城市规划信息集成化和可视化。这不仅为城市规划的决策提供了更加准确、科学的数据支撑,也为市民和企业提供了更加便捷、高效的城市服务。
图扑 HT 曾参与搭建的智慧城市数字孪生项目,在实现城市规划数字化管理的同时,还实现了城市区块、街区、单元等各个层次的数字化管理。还实现了城市交通、公共安全等多个领域的数字化管理,为杭州市民提供了更加便捷、高效的城市服务。
一、城市规划数字化管理
城市规划是智慧城市建设的重要组成部分,而数字孪生技术可以通过数字化城市的各项数据,包括建筑物、道路、公共设施等,实现了城市规划信息集成化和可视化。这不仅为城市规划的决策提供了更加准确、科学的数据支撑,也为市民和企业提供了更加便捷、高效的城市服务。

图扑软件在数字孪生技术应用于城市规划数字化管理方面有着非常成熟的技术和经验。例如,在杭州数字孪生项目中,图扑软件实现了城市区块、街区、单元等多个层次的数字化管理。此外,该项目还实现了城市交通、公共安全等多个领域的数字化管理,为杭州市民提供了更加便捷、高效的城市服务。
二、城市交通管理
随着城市化进程的加速,城市交通问题越来越突出,道路拥堵、交通事故等问题成为制约城市发展的重要因素。而数字孪生技术可以通过数字化城市交通系统,实现交通数据的采集、分析和预测,提高交通系统的智能化和效率。
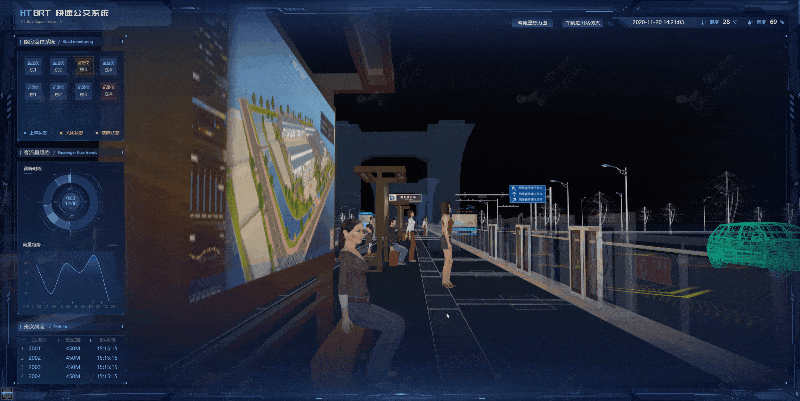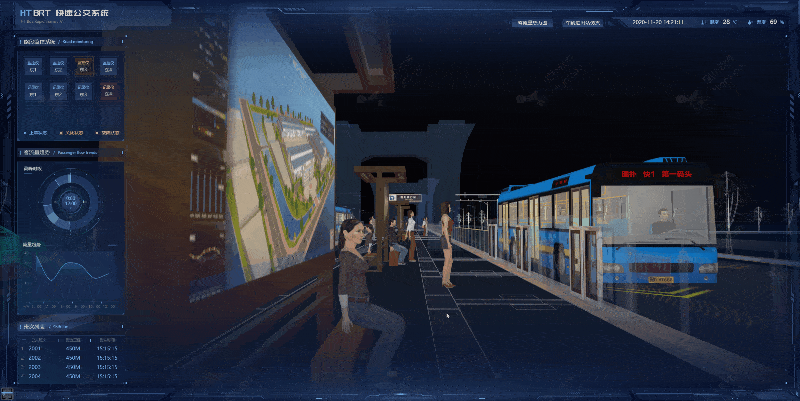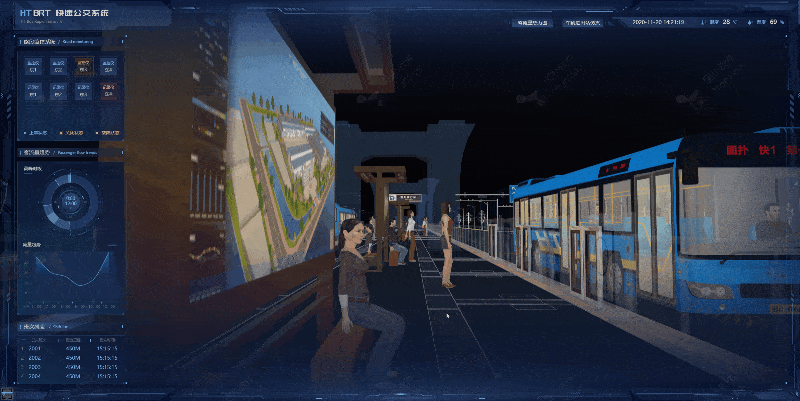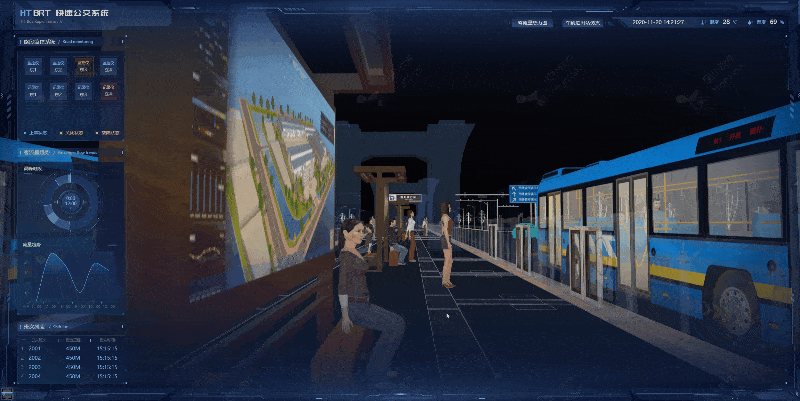
图扑软件在数字孪生技术应用于城市交通管理方面也具有独特的优势。例如,他们可以通过数字孪生技术模拟交通流量变化,优化城市道路规划,提高交通效率,减少拥堵和交通事故。此外,数字孪生技术还可以实现交通路线的智能推荐,为市民提供更加便捷的出行服务。
三、城市公共安全管理
城市公共安全是城市管理的重要领域之一,而数字孪生技术可以通过数字化城市公共安全系统,实现公共安全数据的采集、分析和预测。这不仅可以帮助城市管理者更加直观地了解城市公共安全状况,也可以帮助他们及时发现和解决各种安全问题。
图扑软件在数字孪生技术应用于城市公共安全管理方面也具有独特的优势。例如,可以通过数字孪生技术模拟城市公共安全事件,优化城市公共安全预警机制,提高城市公共安全防控的能力。

四、城市能源管理
城市能源管理是智慧城市建设的重要组成部分,而数字孪生技术可以通过数字化城市能源系统,实现能源数据的采集、分析和预测。这不仅可以帮助城市管理者更加直观地了解城市能源状况,也可以帮助他们及时发现和解决各种能源问题。图扑软件在数字孪生技术应用于城市能源管理方面也具有独特的优势。孪生技术模拟城市能源消耗变化,优化城市能源规划,提高城市能源利用效率。

图扑软件在数字孪生技术应用于城市交通管理方面也具有独特的优势。例如,他们可以通过数字孪生技术模拟交通流量变化,优化城市道路规划,提高交通效率,减少拥堵和交通事故。此外,数字孪生技术还可以实现交通路线的智能推荐,为市民提供更加便捷的出行服务。
数字孪生技术在智慧城市建设中的应用前景十分广阔。而图扑软件作为数字孪生技术的领先企业之一,已经在智慧城市建设中取得了许多成功的应用案例,未来也将会在更多领域实现数字孪生技术的应用和创新。同时,数字孪生技术也将会为智慧城市的建设提供更加科学、准确、高效的技术支持,促进城市管理的智能化和现代化。
相关文章:

智慧城市规划数字化管理:数字孪生技术的创新应用
随着智能城市的不断发展,数字孪生技术也开始在智慧城市的建设中得到了广泛应用。数字孪生作为一种数字化的复制技术,它可以模拟真实世界中的实体和过程。 在城市规划方面,数字孪生可以帮助城市规划师更加直观地了解城市的整体规划和发展趋势&…...

开心档之C++ 指针
C 指针 学习 C 的指针既简单又有趣。通过指针,可以简化一些 C 编程任务的执行,还有一些任务,如动态内存分配,没有指针是无法执行的。所以,想要成为一名优秀的 C 程序员,学习指针是很有必要的。 正如您所知…...
零基础搭建私人影音媒体平台【远程访问Jellyfin播放器】
文章目录 1. 前言2. Jellyfin服务网站搭建2.1. Jellyfin下载和安装2.2. Jellyfin网页测试 3.本地网页发布3.1 cpolar的安装和注册3.2 Cpolar云端设置3.3 Cpolar本地设置 4.公网访问测试5. 结语 转载自内网穿透工具的文章:零基础搭建私人影音媒体平台【远程访问Jelly…...

Abstract Expressionist
古董地图画集 10大最有名的抽象艺术家 抽象表现主义是现代许多不同艺术思想和表达流派中最奇特的艺术运动之一。这场运动开始从社会变革中涌现出来,恰逢第二次世界大战的最后几周和几个月。 这一次,来自世界各地的人们开始欢迎在经历了多年有史以来最致…...
【郭东白架构课 模块二:创造价值】24|节点四:如何减少语义上的分歧?
你好,我是郭东白。上节课我们通过一个篇幅比较长的电商案例,详细展示了为什么在架构活动中会出现语义分歧。同时也描述了,架构师在统一语义这个环节中所要创造的真正价值是什么。即,看到不同角色之间语境的差异,然后通…...

windows下免费本地部署类ChatGpt的国产ChatGLM-6B
ChatGLM-6B 是一个开源的、支持中英双语的对话语言模型,基于 General Language Model (GLM) 架构,具有 62 亿参数。结合模型量化技术,用户可以在消费级的显卡上进行本地部署(INT4 量化级别下最低只需 6GB 显存)。 Chat…...

flask+opencv+实时滤镜(原图、黑白、怀旧、素描)
简介:滤镜,主要是用来实现图像的各种特殊效果。图像滤镜用于改变图像的视觉效果,使其具有特定的风格。下面是这三种滤镜的详细说明: 1、黑白(Grayscale):黑白滤镜将彩色图像转换为灰度图像&…...
计算机算法类SCI,数据库稳定检索19年)
【SCI征稿】极速送审,中科院2区(TOP)计算机算法类SCI,数据库稳定检索19年
算法类: 检索年份:数据库稳定检索19年 自引率:14.50% 国人占比:22.78% 期刊简介:IF:8.0-9.0,JCR1区,中科院2区(TOP) 检索情况:SCI&EI 双…...
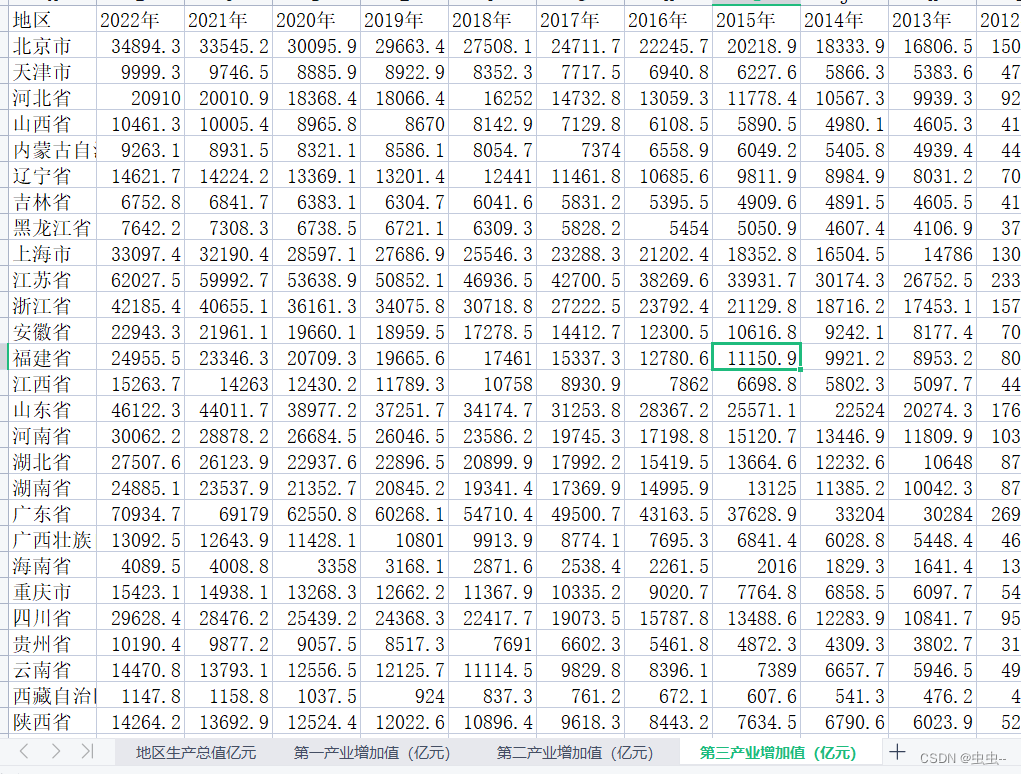
1992-2022年31省GDP、第一产业增加值、第二产业增加值 第三产业增加值
1992-2022年31省GDP、第一产业增加值、第二产业增加值 第三产业增加值 1、时间:1992-2022年 2、范围:包括31省 3、指标:省GDP、省第一产业增加值、省第二产业增加值、省第三产业增加值 4、缺失情况说明:无缺失 5、来源&#…...

100种思维模型之万物系统思维模型-57
前面我们介绍过 “万物联系思维模型” ,即万物之间存有各种各样的联系,在解决问题时要看到事物之间的连接,并找到关键的连接,继而快速的解决问题。 01 何谓万物系统思维模型 一、万物系统思维 人的思维习惯, 一…...
)
Java 中的包装类是什么?如何使用包装类来操作基本数据类型(二十二)
Java 中的包装类是一种特殊的类,用来将基本数据类型(如 int、double、char 等)包装成对象。包装类的作用是可以让基本数据类型具有对象的特性,比如可以作为参数传递给泛型类或方法,可以调用对象的方法,可以…...
【Python入门】Pycharm的使用指南
前言 📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于Python零基础入门系列,本专栏主要内容为Python基础语法、判断、循环语句、函…...
python搭建HaIcon物联平台!
Python是一种高级编程语言,易于学习和理解。它在各个领域都有着广泛的应用,例如数据科学、机器学习、爬虫等。 在Python的强大功能之外,Python还有着丰富的第三方库和框架,其中之一就是HaIcon。HaIcon是一种基于Python的物联网平台,它提供了完整的解决方案,包括设备管理…...
GUI编程(二)
Swing Swing是GUI(图形用户界面)开发工具包。 早期的AWT(抽象窗口工具包)组件开发的图形用户界面,要依赖本地系统,当把AWT组件开发的应用程序移植到其他平台的系统上运行时,不能保证其外观风格…...
俩小伙一晚上写了个 AI 应用,月入两万??(文末附开发教程)
开发出一款能够与 AI 对话生成和编辑思维导图的工具,听起来似乎只能是一群专业的 AI 背景团队花费大量的时间和精力训练模型,打磨应用才能完成的事情。 但是,两名大学生却在一夜之间完成了,就像炼金术士将庸俗的材料转化成黄金一…...

Python爬虫常用框架
大家都知道python是一门多岗位编程语言,学习python之后可以从事的岗位有很多,python爬虫便在其中,不过很多人对python不是很了解,所以也不知道python爬虫是什么,接下来小编为大家介绍一下。 Python是一门非常适合开发…...

2023亚马逊云科技研究,数字化技能为中国企业和员工带来经济效益
在中国,信息技术在个人、企业和宏观经济层面都推动着重大变革。为了研究这些变化所带来的影响,盖洛普咨询公司(Gallup)和亚马逊云科技开展了关于数字化技能的调研。 研究表明,数字化技能正在为中国企业和在职人员带来巨大的经济价值&#x…...
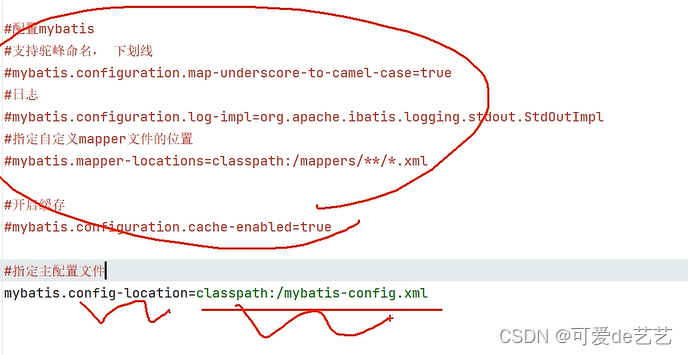
springboot使用mybatis
扫描mapper接口的位置,生成代理对象 在application.properties配置数据源 测试: 在application.properties配置mybaits,支持驼峰命名,下划线 结果映射: Insert语句例子 在application.properties配置日志 更新 总结: 结果复用 ResultMap第二种…...
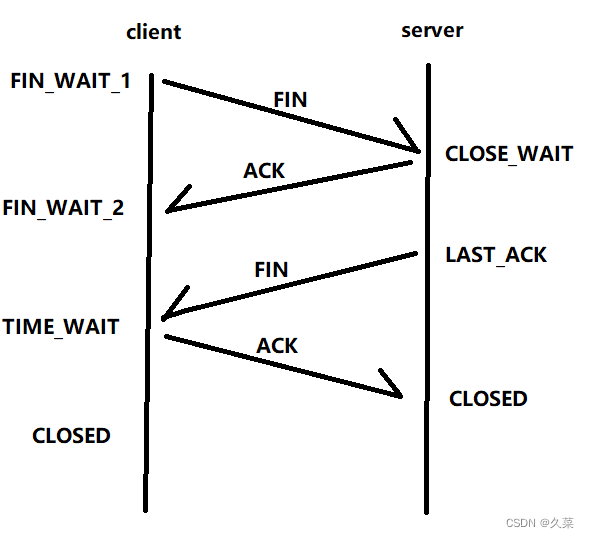
为什么是三次握手和四次挥手
文章目录 为什么是三次握手为什么是四次挥手什么是TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法 为什么是三次握手 因为这是双方都有收发的最小次数 握手的目的:确认网络好着没,对方好着没 确认双方主机是否健康(双方)…...
 总结)
Codeforces Round 867 (Div 3) 总结
文章目录 ABCDE 文章首发于我的个人博客:欢迎大佬们来逛逛 Dashboard - Codeforces Round 867 (Div. 3) - Codeforces A 题目大意:有n个电视节目,每个电视节目占据一定的时间,并且具有一个娱乐值,一秒可以额换一次台…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
