常量与变量:编程中重要的两种数据类型
常量与变量
在编程中,我们常常需要存储一些数据。这些数据有些是恒定不变的,有些却是可以随时变化的。对于恒定不变的数据,我们称之为常量;对于可以变化的数据,我们则称之为变量。这两种数据类型在程序中非常重要,我们来看看它们的区别和使用。
常量
常量是一种恒定不变的量。在程序中,常量一旦被定义后就不可以再次赋值,其值保持不变。通常常量的定义时使用 const 关键字。例如:
const int A = 10;
这个常量 A 被定义为整数类型,初始值为 10。在程序中,如果我们尝试去修改 A 的值,会受到编译器的警告。
常量的作用在于:我们可以使用名字来指代某个值,并且确保这个值在程序执行期间不会改变,这样可以提高程序的可读性和可维护性。
变量
相比之下,变量则是可以随时更改的值。它们是程序中最重要的数据类型之一。在程序中,我们需要存储一些值,这些值有时会随着程序的执行而改变,这就是变量的作用。我们可以使用变量来存储一段数据,然后随时更改这个数据。例如:
int B = 100;
这个变量 B 被定义为整数类型,初始值为 100。在程序中,我们可以随时更改 B 的值来存储一个新的整数值。
变量和常量的最大区别在于,变量在程序执行期间可以随时更改,而常量的值始终保持不变。这使得变量非常适合存储需要经常更改的数据,而常量则适合存储恒定的值,避免了程序中的错误。
举例说明
假设我们有一个程序需要计算一个正方形的周长和面积。我们可以使用变量和常量来存储这些值。例如:
const int side_length = 10; // 正方形的边长为 10
int perimeter = 4 * side_length; // 计算周长
int area = side_length * side_length; // 计算面积
在这个例子中,我们使用常量 side_length 来存储正方形的边长。因为正方形的边长是恒定不变的,所以我们使用常量来表示它。然后,我们使用两个变量 perimeter 和 area 来分别计算正方形的周长和面积。这两个变量存储的值可以随时更改,因为它们的值在程序执行期间可能会改变。
总结
常量和变量是编程中非常重要的两种数据类型。常量是恒定不变的值,而变量可以随时更改。在程序中,我们需要适当地使用常量和变量来存储数据,以提高程序的可读性和可维护性。
相关文章:

常量与变量:编程中重要的两种数据类型
常量与变量 在编程中,我们常常需要存储一些数据。这些数据有些是恒定不变的,有些却是可以随时变化的。对于恒定不变的数据,我们称之为常量;对于可以变化的数据,我们则称之为变量。这两种数据类型在程序中非常重要&…...
( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度:中等 给定一个包含 n 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。 你…...

【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...

武忠祥老师每日一题||定积分基础训练(三)
常用的基本不等式: sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...

Docker安装常用软件-Apollo(有问题)
零:apollo概念介绍 官网网站:GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址:mirrors / ctripcorp / apollo GitCode …...

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...
)
如何使用二元三次回归分析建立预测模型?(分析、原理、代码示例)
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型,常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型,其中包括两个自变量(通常…...
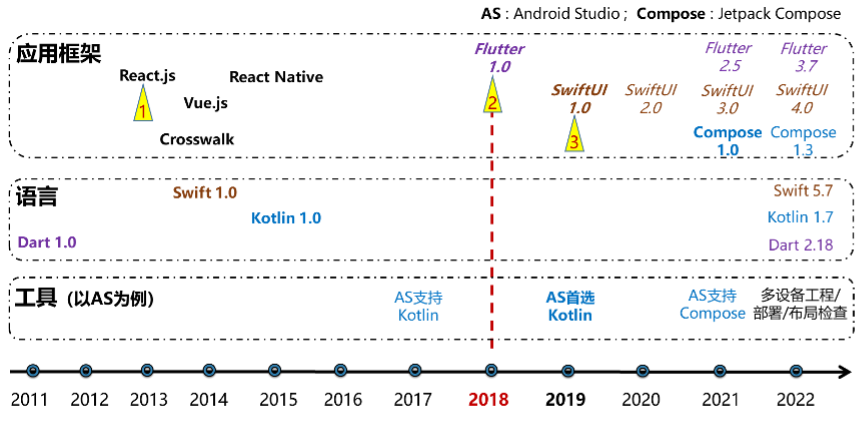
面向万物智联的应用框架的思考和探索(上)
原文:面向万物智联的应用框架的思考和探索(上),点击链接查看更多技术内容。 应用框架,是操作系统连接开发者生态,实现用户体验的关键基础设施。其中,开发效率和运行体验是永恒的诉求,…...

《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习,是一个交叉学科,是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期,使用专家设计的规则体系来设计。 缺点&…...

ClickHouse 内存管理是如何实现的
概述 本文介绍Clickhouse内存管理的实现原理。通过本文的分析,可以对Clickhouse的内存管理有一个概要的理解。 Clickouse内存管理组成 ClickHouse 使用内存管理系统来控制内存资源的分配和释放。内存管理系统的主要组成部分是: 内存池:Cl…...

docker容器技术
什么是docker Docker 使用 Google 公司推出的 Go 语言 进行开发实现,基于 Linux 内核的 cgroup,namespace,以及 OverlayFS 类的 Union FS 等技术,对进程进行封装隔离,属于 操作系统层面的虚拟化技术。由于隔离的进程独…...
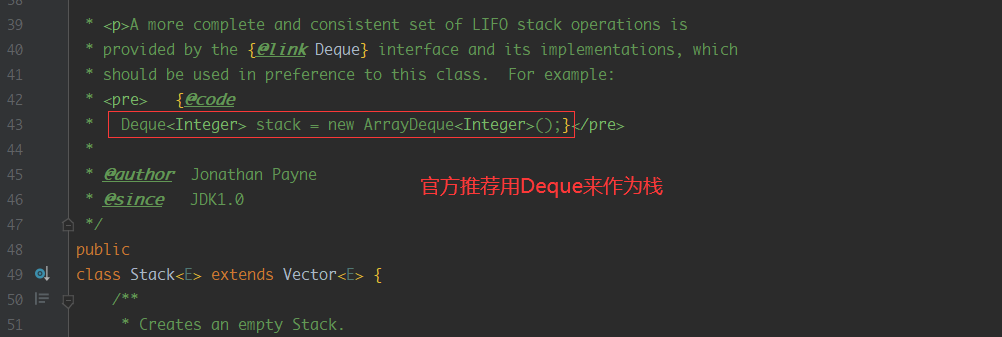
设计模式七大设计原则
文章目录 1、什么是设计模式2、单一职责原则3、开闭原则4、接口隔离原则5、依赖倒置原则6、迪米特法则(最少知道原则)7、里式替换原则8、组合优于继承 设计模式主要是为了满足一个字 变,这个字,可能是需求变更、可能是场景变更&a…...
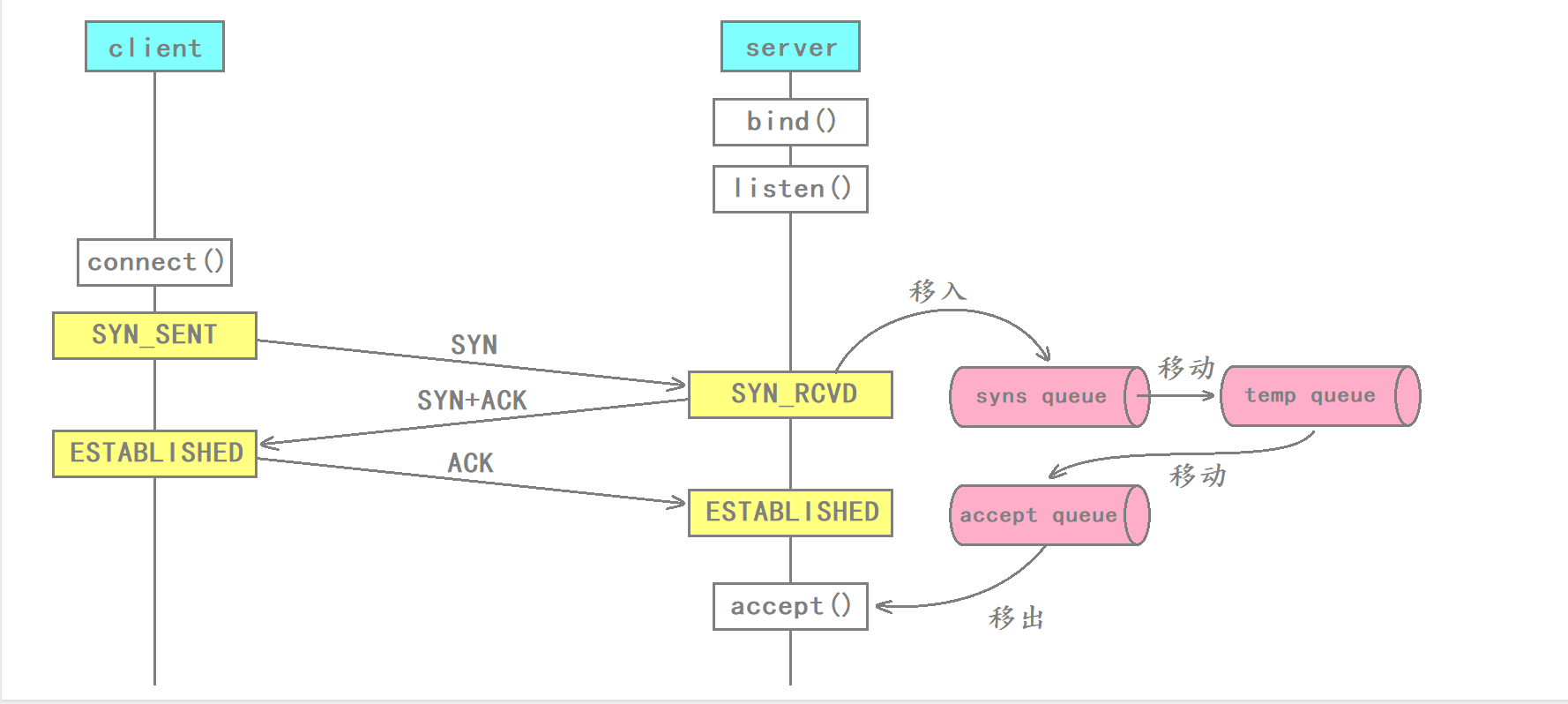
【Hello Network】TCP协议相关理解
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:补充下对于TCP协议的各种理解 TCP协议相关实验 TCP相关试验理解CLOSE_WAIT状态理解TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法理解listen的…...

实施CRM目标有哪几步?如何制定CRM目标?
在当今竞争激烈的商业环境中,与客户建立持久的关系是企业重要的工作。CRM客户管理系统能有效帮助企业管理优化流程、管理客户,提高销售成功率,推动收入增长。那么您了解如何实施CRM吗?下面说说实施CRM目标是什么,如何设…...
船舶建造概论(船舶建造工艺任务与现代造船模式)
船舶建造概论 1 船舶建造概论1.1 船舶建造工艺主要任务1.2 船舶建造流程(1)钢材料预处理(2) 钢材料加工(3)分段制作(4)总段制作(5)船台合拢(6&…...

项目内训(2023.5.6)
目录 Nacos是什么? 领域模型是什么? domain模块一般是干什么的? 在小乌龟中合并其他分支的作用是什么? nacos的配置文件 服务集群、服务提供、服务更加灵活庞大、消费服务、访问比较麻烦,A和B服务一起访问 系统结…...

【操作系统OS】学习笔记第二章 进程与线程(下)【哈工大李治军老师】
基于本人观看学习 哈工大李治军老师主讲的操作系统课程 所做的笔记,仅进行交流分享。 特此鸣谢李治军老师,操作系统的神作! 如果本篇笔记帮助到了你,还请点赞 关注 支持一下 ♡>𖥦<)!! 主页专栏有更多࿰…...
)
Linux命令集(Linux文件管理命令--rmdir指令篇)
Linux命令集(Linux文件管理命令--rmdir指令篇) Linux文件管理命令集(rmdir指令篇)5. rmdir(remove directory)1. 删除空的目录 folder12. 强制删除目录 folder1(包括非空目录)3. 递归删除目录及其目录下所有…...

在技术圈超卷的当下,学历到底是敲门砖还是枷锁?
前言 最近,突然之间被“孔乙己文学”刷屏了,短时间内“孔乙己文学”迅速走红,孔乙己是中国文学中的一位经典人物,他的长衫被认为是他的象征之一,孔乙己的长衫折射出很多现象,既有社会的,也有教育…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
