( 数组和矩阵) 645. 错误的集合 ——【Leetcode每日一题】
❓645. 错误的集合
难度:简单
集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字重复 。
给定一个数组 nums 代表了集合 S 发生错误后的结果。
请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
示例 1:
输入:nums = [1,2,2,4]
输出:[2,3]
示例 2:
输入:nums = [1,1]
输出:[1,2]
提示:
- 2 < = n u m s . l e n g t h < = 1 0 4 2 <= nums.length <= 10^4 2<=nums.length<=104
- 1 < = n u m s [ i ] < = 1 0 4 1 <= nums[i] <= 10^4 1<=nums[i]<=104
💡思路:
法一:交换数组元素
最直接的方法是先对数组进行排序,这种方法时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。本题可以以 O ( n ) O(n) O(n) 的时间复杂度、 O ( 1 ) O(1) O(1) 空间复杂度来求解。
- 主要思想是通过交换数组元素,使得数组上的元素在正确的位置上;
- 这样只有 重复的数 出现在 丢失整数 的位置上。
法二:哈希表
重复的数字在数组中出现 2 次,丢失的数字在数组中出现 0次,其余的每个数字在数组中出现 1 次。因此可以使用哈希表记录每个元素在数组中是否出现
- 如果出现两次,则找到了重复的数;
- 将所有数都存到哈希表,再遍历哈希表,则可找到丢失的数;
🍁代码:(Java、C++)
法一:交换数组元素
Java
class Solution {public int[] findErrorNums(int[] nums) {for(int i = 0; i < nums.length; i++){while(nums[i] != i + 1 && nums[i] != nums[nums[i] - 1]){swap(nums, i, nums[i] - 1);}}for(int i = 1; i <= nums.length; i++){if(nums[i - 1] != i){return new int[]{nums[i - 1], i};}}return null;}private void swap(int[] nums, int i, int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}
C++
class Solution {
public:vector<int> findErrorNums(vector<int>& nums) {for(int i = 0; i < nums.size(); i++){while(nums[i] != i + 1 && nums[i] != nums[nums[i] - 1]){swap(nums, i, nums[i] - 1);}}for(int i = 1; i <= nums.size(); i++){if(nums[i - 1] != i){return {nums[i - 1], i};}}return {};}void swap(vector<int>& nums, int i, int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
};
法二:哈希表
Java
class Solution {public int[] findErrorNums(int[] nums) {HashSet<Integer> s = new HashSet<>();int repeat = 0, lose = 0;for(int num : nums){if(s.contains(num)) repeat = num;s.add(num);}for(int i = 1; i <= nums.length; i++){if(!s.contains(i)){lose = i;break;}}return new int[]{repeat, lose};}
}
C++
class Solution {
public:vector<int> findErrorNums(vector<int>& nums) {unordered_set<int> s;int repeat = 0, lose = 0;for(int num : nums){if(s.find(num) != s.end()) repeat = num;s.insert(num);}for(int i = 1; i <= nums.size(); i++){if(s.find(i) == s.end()){lose = i;break;}}return {repeat, lose};}
};
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中
n为数组的长度。 - 空间复杂度: O ( 1 ) O(1) O(1),法一只需常量级空间;而哈希表需要创建大小为 O ( n ) O(n) O(n) 的哈希表,空间复杂度为 O ( n ) O(n) O(n)。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 645. 错误的集合 ——【Leetcode每日一题】
❓645. 错误的集合 难度:简单 集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字重复 。 给定一个数组 nums 代表了…...

2023年全国最新道路运输从业人员精选真题及答案63
百分百题库提供道路运输安全员考试试题、道路运输从业人员考试预测题、道路安全员考试真题、道路运输从业人员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 119.在危险货物道路运输过程中,(&#x…...
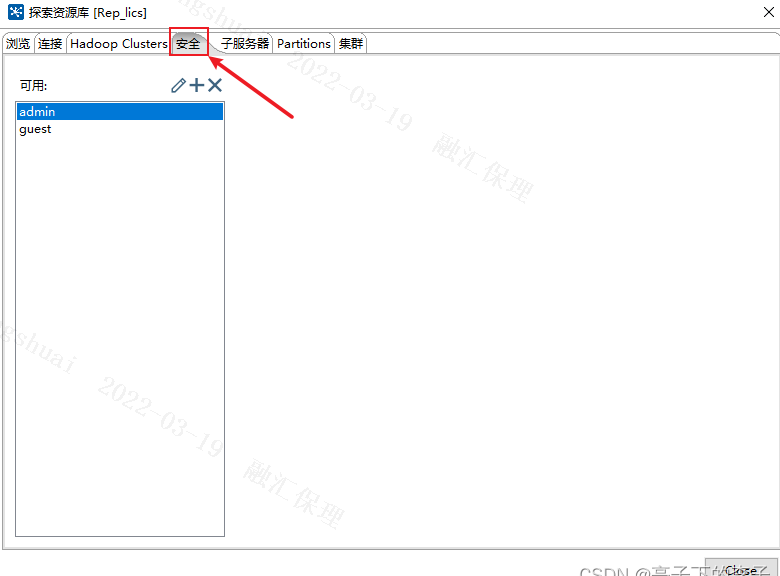
Kettle安装与使用
一、Kettle简介 Kettle最早是一个开源的ETL(Extract-Transform-Load的缩写)工具,全称为KDE Extraction, Transportation, Transformation and Loading Environment。后来Kettle重命名为Pentaho Data Integration 。它由Java开发,…...
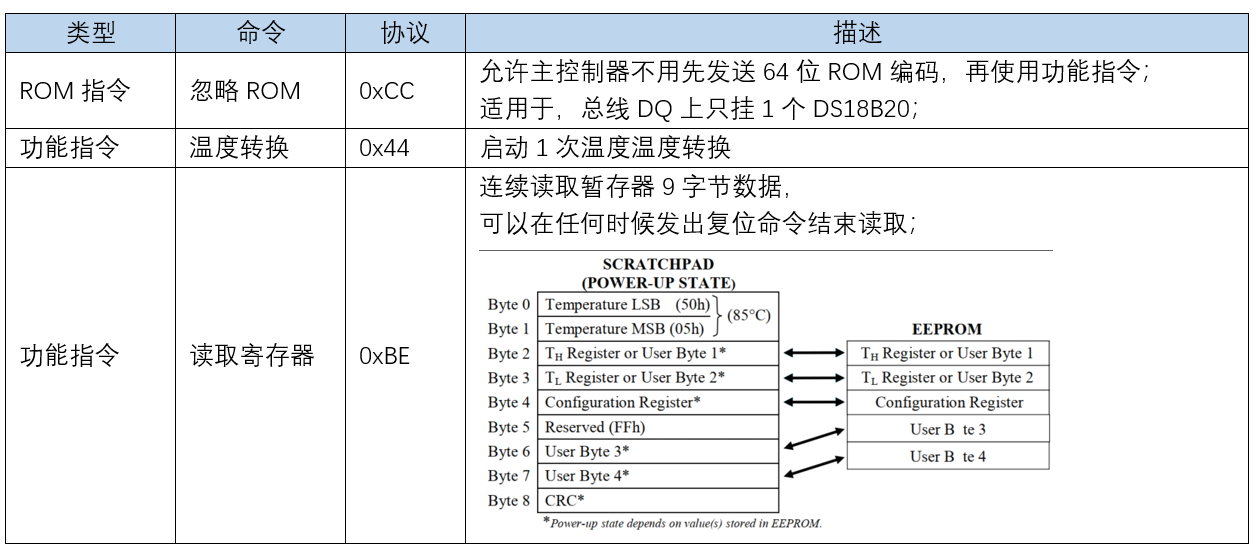
C51 - DS18B20
Thermometer 1> 实验概述2> 硬件设计3> DS18B203.1> 原理框图3.2> 数据格式 4> 单总线(1-Wire)通讯协议4.1> 初始化(复位)时序4.2> 写-DS18B20时序4.3> 读-DS18B20时序4.4> 命令 5> 程序设计5.1…...
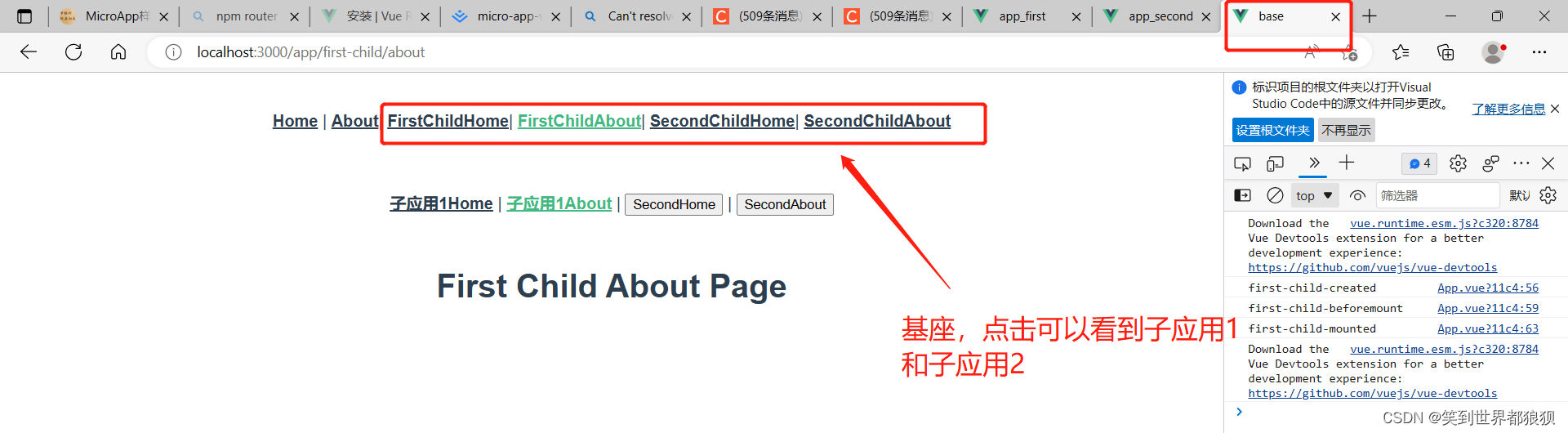
手把手教你使用vue2搭建微前端micro-app
简述 本文主要讲述新手小白怎么搭建micro-app,几乎是每一步都有截图说明。上手应该很简单。 研究背景 这段时间在网上找了很多有关微前端相关的知识,起初本来是想着先搭建一个single-spa,但是奈何网上能找到的内容都是千篇一律。我也是…...

DDR3(MIG核配置官方demoFPGA代码实现及仿真)
由于直接对 DDR3 进行控制很复杂,因此一般使用 MIG IP 来实现,同时为了更简单地使用 MIG IP,我们采用 AXI4 总线协议进行控制。下面首先介绍 MIG IP 的配置,然后看看官方 demo (里面包含一个仿真要用到的 DDR3 模型&am…...

传奇人物《周兴和》书连载之67 不辱神圣的使命
不辱神圣的使命 这里,先前还是一个十分神秘的地方。 外人和车辆要想进入这片区域,那是绝对不允许的。这片区域隐于群山之中,且戒备森严,外人若想进入,那是要经过好几道政治审查和随身检查的。近年来,随着…...

Spring框架中的单例Beans是线程安全的么?
在Spring框架中,单例Beans默认是线程安全的。 当你在Spring框架中声明一个单例Bean并配置为默认的单例作用域时,Spring会确保对该Bean的并发访问是线程安全的。以下是一个简单的代码演示: 假设我们有一个名为 SingletonBean 的单例 Bean 类…...

AI脚本插件开发-链接图自动建立档名-插件制作源码-illustrator插件开发
文章目录 1.illustrator1.1.app.activeDocument1.2.selection2.模块分析3.源码工程4.功能描述5.作者答疑本文主要分析一款插件的源码,链接图自动建立档名,代码一般较长,读者耐心阅读,对于学习插件开发具有不小的帮助。先介绍了一下基础资料,如有不懂的地方,就去这些资料里…...

rust智能指针
智能指针 智能指针虽然也号称指针,但是它是一个复杂的家伙:通过比引用更复杂的数据结构,包含比引用更多的信息,例如元数据,当前长度,最大可用长度等。引用和智能指针的另一个不同在于前者仅仅是借用了数据…...

Git、Gitee、Github、Gitlab区别与联系
Git:本地软件,无需联网即可使用,实现本地代码的管理。 分布式版本控制系统,是一种工具,用于代码的存储和版本控制。 将本地文件通过一定的操作将其同步上传到Github或Gitee Gitee:是一家中…...

接口优化的策略
1.批处理 批量思想:批量操作数据库,这个很好理解,我们在循环插入场景的接口中,可以在批处理执行完成后一次性插入或更新数据库,避免多次IO。 //批量入库 batchInsert();List的安全操作有以下几种方式: 使…...

android 隐藏底部虚拟按键
方法一 滑动屏幕 可重新显示出来 protected void hideBottomUIMenu() { //隐藏虚拟按键,并且全屏 if (Build.VERSION.SDK_INT <11 && Build.VERSION.SDK_INT < 19) { // lower api View v this.getWindow().getDecorView(); v.setSyst…...
基于电流控制的并网逆变器(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
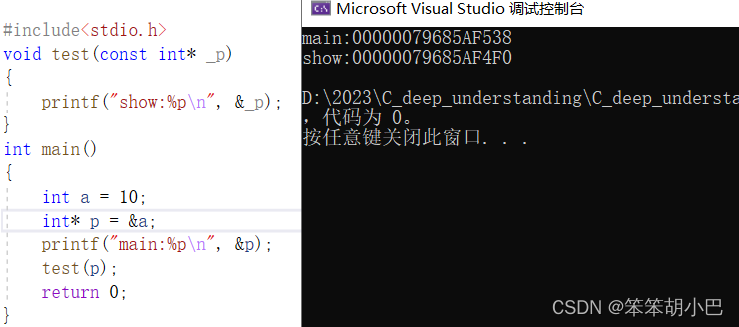
learn_C_deep_9 (汇编角度理解return的含义、const 的各种应用场景)
return 关键字 不知道我们大家是否有一个疑惑:我们下载一个大型游戏软件(王者荣耀),都要花几个小时去下载,但是一旦我们游戏连输,想要删除这个软件的时候,它仅仅只需要十几秒,这是为…...

基于深度学习的OCR技术
随着数字化时代的到来,图片识别技术越来越受到人们的关注。其中,OCR技术作为图片处理的一个重要分支,可以将扫描的图片进行自动识别和分类,极大地提高了工作效率。本文将介绍有道实况OCR技术的相关内容,帮助读者更好地…...
『python爬虫』09. bs4实战之下载精美壁纸(保姆级图文)
目录 爬取思路代码思路1.拿到主页面的源代码. 然后提取到子页面的链接地址, href2.通过href拿到子页面的内容. 从子页面中找到图片的下载地址 img -> src3.下载图片 3. 完整实现代码总结 欢迎关注 『python爬虫』 专栏,持续更新中 欢迎关注 『python爬虫』 专栏&…...
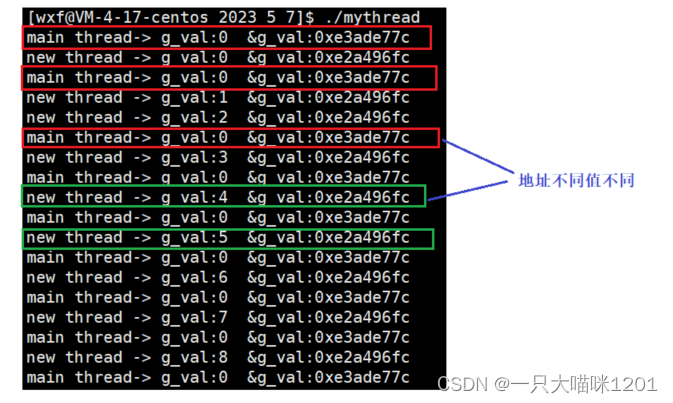
【Linux学习】多线程——线程控制 | 线程TCB
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 线程控制 | 线程TCB 🧰线程控制🎴线程创建🎴线程结束…...
Node 10 接口
接口 简介 接口是什么 接口是 前后端通信的桥梁 简单理解:一个接口就是 服务中的一个路由规则 ,根据请求响应结果 接口的英文单词是 API (Application Program Interface),所以有时也称之为 API 接口 这里的接口指的是『数据接口』&#…...

大型互联网企业大流量高并发电商领域核心项目已上线(完整流程+项目白皮书)
说在前面的话 面对近年来网络的飞速发展,大家已经都习惯了网络购物,从而出现了一些衍生品例如:某宝/某东/拼夕夕等大型网站以及购物APP~ 并且从而导致很多大型互联网企业以及中小厂都需要有完整的项目经验,以及优秀处理超大流量…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
