太原网站建设dweb/广州专门做seo的公司
随着数字化时代的到来，图片识别技术越来越受到人们的关注。其中，OCR技术作为图片处理的一个重要分支，可以将扫描的图片进行自动识别和分类，极大地提高了工作效率。本文将介绍有道实况OCR技术的相关内容，帮助读者更好地了解这项技术。
一、有道实况OCR技术的原理
有道实况OCR技术是一种基于计算机视觉的图像识别技术，它可以自动识别图片中的文字信息，并将其转换为可编辑的文本格式。该技术的实现原理是利用计算机视觉技术和深度学习算法，对图片进行快速扫描和处理，以便对其中的文字进行识别。
具体来说，有道实况OCR技术主要包括以下几个步骤：
1、图片预处理：对待识别的图片进行预处理，包括灰度化、二值化、图像增强等操作，以便提高识别的准确度。
2、文字检测：使用计算机视觉技术对图片中的文字进行检测和识别。可以使用预训练的模型，也可以使用深度学习算法进行自动识别。
3、文字识别：将检测到的文字信息转换为可编辑的文本格式。常用的文字识别算法包括基于深度学习的神经网络、基于规则的方法、基于统计的方法等。
4、后处理：对识别结果进行后处理，包括对识别结果进行格式化、去除噪声、添加注释等操作，以便提高识别结果的可读性和可用性。
二、有道实况OCR技术的优势
相比于传统的OCR技术，有道实况OCR技术具有以下优势：
1、实时性强：有道实况OCR技术可以在图片扫描后立即对其中的文字进行识别，大大提高了工作效率。
2、识别准确度高：有道实况OCR技术采用了多种先进的识别算法，并且对图片进行了预处理和增强，识别准确度较高。
3、适用范围广：有道实况OCR技术可以识别多种语言和字体，并且对图片的尺寸和格式没有限制。
4、应用广泛：有道实况OCR技术可以广泛应用于文档管理、数字签名、身份认证等领域。
三、有道实况OCR技术的应用场景
有道实况OCR技术在文档管理、数字签名、身份认证等领域有着广泛的应用。例如，在文档管理领域，有道实况OCR技术可以将扫描的图片自动识别并转换为可编辑的文本格式，从而提高了文档管理的效率。在数字签名领域，有道实况OCR技术可以将签名图片自动识别并转换为可编辑的文本格式，从而实现了数字签名的自动化。在身份认证领域，有道实况OCR技术可以将身份证、护照等图片自动识别并转换为可编辑的文本格式，从而实现了身份认证的自动化。
本文由 mdnice 多平台发布
相关文章：
基于深度学习的OCR技术
随着数字化时代的到来，图片识别技术越来越受到人们的关注。其中，OCR技术作为图片处理的一个重要分支，可以将扫描的图片进行自动识别和分类，极大地提高了工作效率。本文将介绍有道实况OCR技术的相关内容，帮助读者更好地…...
『python爬虫』09. bs4实战之下载精美壁纸（保姆级图文）
目录 爬取思路代码思路1.拿到主页面的源代码. 然后提取到子页面的链接地址, href2.通过href拿到子页面的内容. 从子页面中找到图片的下载地址 img -> src3.下载图片 3. 完整实现代码总结 欢迎关注 『python爬虫』 专栏，持续更新中 欢迎关注 『python爬虫』 专栏&…...
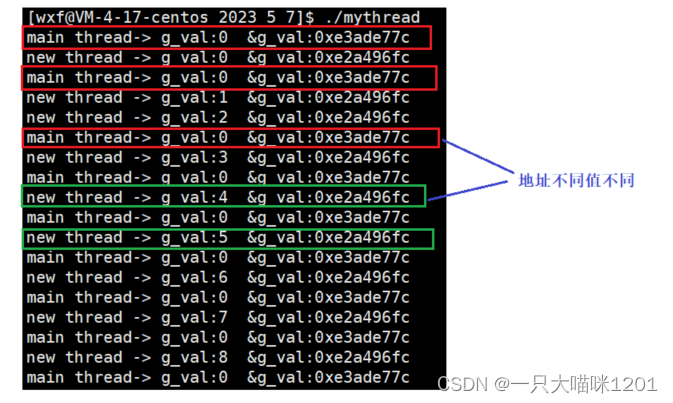
【Linux学习】多线程——线程控制 | 线程TCB
🐱作者：一只大喵咪1201 🐱专栏：《Linux学习》 🔥格言：你只管努力，剩下的交给时间！ 线程控制 | 线程TCB 🧰线程控制🎴线程创建🎴线程结束…...
Node 10 接口
接口 简介 接口是什么 接口是 前后端通信的桥梁 简单理解：一个接口就是 服务中的一个路由规则 ，根据请求响应结果 接口的英文单词是 API (Application Program Interface)，所以有时也称之为 API 接口 这里的接口指的是『数据接口』&#…...
大型互联网企业大流量高并发电商领域核心项目已上线(完整流程+项目白皮书)
说在前面的话 面对近年来网络的飞速发展，大家已经都习惯了网络购物，从而出现了一些衍生品例如：某宝/某东/拼夕夕等大型网站以及购物APP~ 并且从而导致很多大型互联网企业以及中小厂都需要有完整的项目经验，以及优秀处理超大流量…...
汇编语言学习笔记六
flag 寄存器 CF:进位标志位，产生进位CF1，否则为0 PF:奇偶位，如010101b，则该数的1有3个，则PF0,如果该数的1的个数为偶数，则PF1。0也是偶数 ZF:在相关指令执行后（运算和逻辑指令，传送指…...
多商户商城系统-v2.2.3版本发布
likeshop多商户商城系统-v2.2.3版本发布了！主要更新内容如下 新增 1.用户端退出账号功能 优化 1.平台添加营业执照保存异常问题 2.平台端分销商品优化-只显示参与分销的商品 3.优化订单详情显示营销价格标签 4.平台交易设置增加默认值 5.种草社区评论调整&a…...
科研人必看入门攻略（收藏版）
来源：投稿 作者：小灰灰 编辑：学姐 本文主要以如何做科研，日常内功修炼，常见科研误区，整理日常‘好论文’四个部分做以介绍，方便刚入门的科研者进行很好的规划。 1.如何做科研 1.1 选方向 当我…...
第5章 循环和关系表达式
1. strcmp()//比较字符串数组是否相等| string 可以直接用“”来判断 char word[5] "aaaa"; strcmp(word,"aaab");//相同输出0，不同输出1; 2. 延时函数 #include<ctime>float sec 2.3;long delay sec*CLOCKS_PER_SEC;long start c…...
Scalable Vector Graphics (SVG)中的svg、clipPath、mask元素
Scalable Vector Graphics (SVG)是一种用于描述二维向量图形的XML基础标记语言。使用SVG可以实现丰富的图形效果，而不需要像使用位图那样考虑分辨率和像素密度的问题，可以在不同设备上展示出相同的高质量图像。 在SVG中，除了基本形状如circl…...
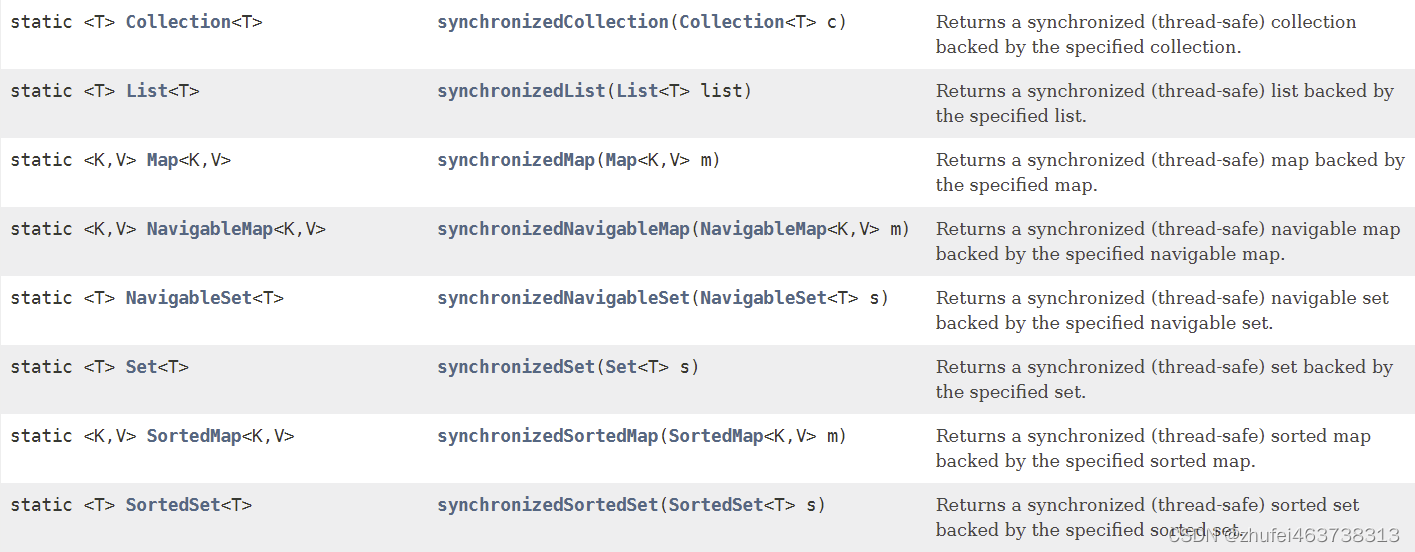
Java基础（十五）集合框架
1. 集合框架概述 1.1 生活中的容器 1.2 数组的特点与弊端 一方面，面向对象语言对事物的体现都是以对象的形式，为了方便对多个对象的操作，就要对对象进行存储。另一方面，使用数组存储对象方面具有一些弊端，而Java 集合…...
安装gitea
1、安装包（gitea-1.13.1-linux-amd64）上传到服务器，并添加执行权限 链接：https://pan.baidu.com/s/1SAxko0RhVmmD21Ev_m5JFg 提取码：ft07 chmod x gitea-1.13.1-linux-amd64 2、执行 ./gitea-1.13.1-linux-amd64 web…...
Java异常处理传递规范总结
java 异常分类 Thorwable类（表示可抛出）是所有异常和错误的超类，两个直接子类为Error和Exception，分别表示错误和异常。其中异常类Exception又分为运行时异常(RuntimeException)和非运行时异常， 这两种异常有很大的区别…...
2d俯视视角游戏，可以切换多种枪械
文章目录 一、 介绍二、 人物移动、鼠标控制转向三、子弹脚本四、子弹随机抛壳五、 爆炸特效六、 发射子弹七、 子弹、弹壳对象池八、 散弹枪九、 火箭弹、发射火箭十、 下载工程文件 一、 介绍 2d俯视视角游戏。 人物视角跟随鼠标移动 多种枪械 抛壳效果 多种设计效果 对象池…...
大四的告诫
保研/考研方向就绩点，（各种）比赛，（考研）刷题为主 工作就算法（比赛），项目，实习为主 👂 LOCK OUT - $atori Zoom/KALONO - 单曲 - 网易云音乐 &…...
滚珠螺杆在设备上的应用
滚珠螺杆跟直线导轨一样，是很多机械设备上不可或缺的重要部件，它是确保机器能够具备高加工精度的前提条件，因此本身对于精度的要求也相当地高。今天，我们就来了解一下滚珠螺杆在不同设备上的应用吧！ 1、大型的加工中心…...
Day41线程同步
线程同步 案例：三个窗口卖100张票 //定义一个类SellTicket实现Runnable接口，定义成员变量100张票 public class SellTicket implements Runnable{private int tickets 100;//重写run方法Overridepublic void run(){while (true){ //没有票后&…...
设计模式之享元模式
参考资料 曾探《JavaScript设计模式与开发实践》；「设计模式 JavaScript 描述」享元模式设计模式之享元模式Javascript 设计模式 - 享元模式 定义 享元模式的英文叫：Flyweight Design Pattern。享元设计模式是用于性能优化的模式，这种设计…...
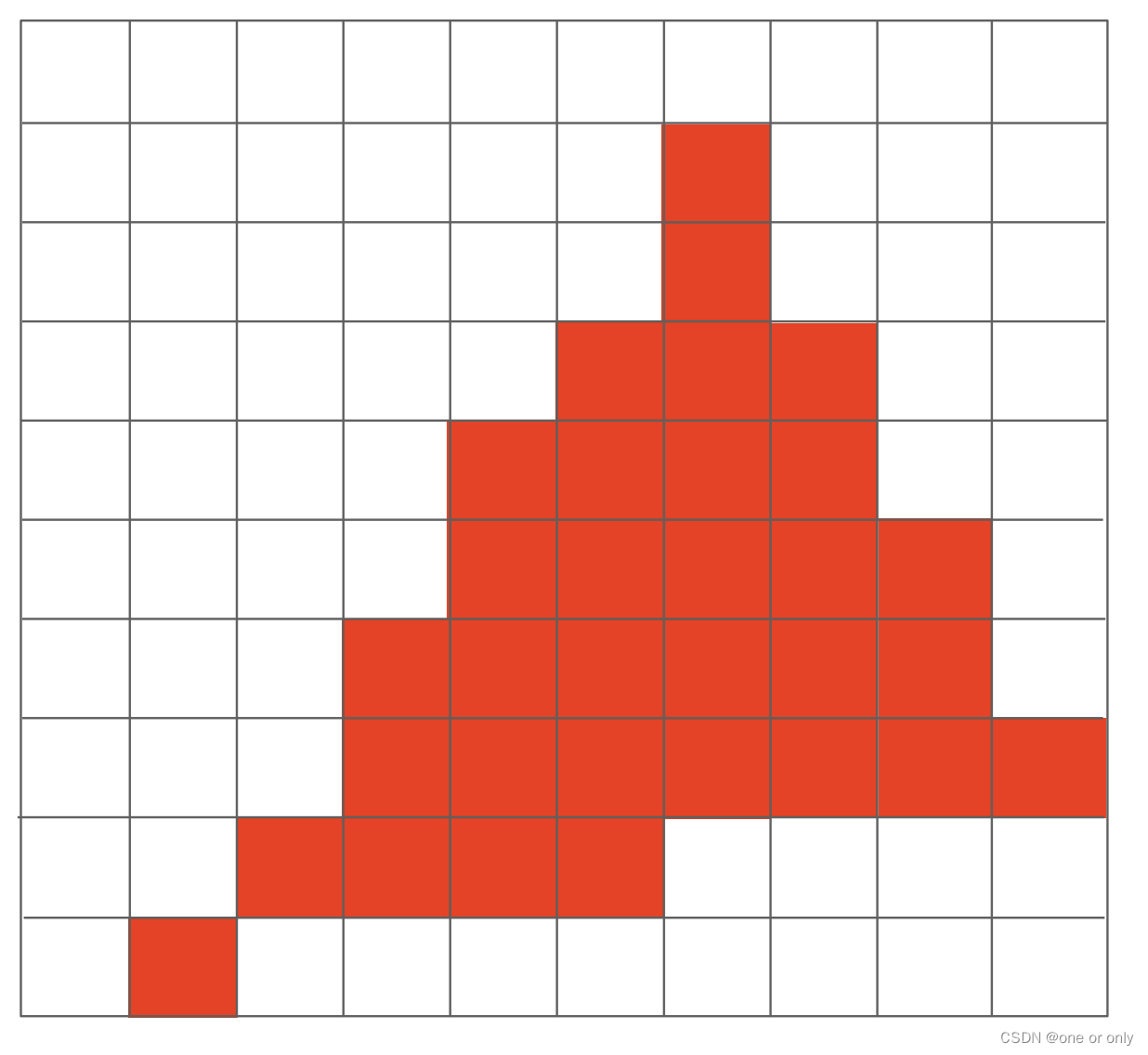
【GAMES101】05 Rasterization（Triangles）
光栅化过程：将一系列变换后的三角形转换为像素的过程。 三角形在图形学中得到很多的应用。 最基础的多边形（边数最少）。任何多边形都可以拆成三角形。性质：三角形内部一定是平面的。三角形内外部定义非常清楚。定义三个顶点后&a…...
13. Pod 从入门到深入理解（二）
本章讲解知识点 Pod 容器共享 VolumeConfigMapSecretDownward APIEmptyDir VolumeHostPath Volume1. Pod 容器共享 Volume 1.1. Volume 的背景及需要解决的问题 存储是必不可少的，对于服务运行产生的日志、数据，必须有一个地方进行保存，但是我们的容器每一次重启都是“恢复…...
ORBBEC（奥比中光）AstraPro相机在ROS2下的标定与D2C（标定与配准）
文章目录 1.rgb、depth相机标定矫正1.1.标定rgb相机1.2.标定depth相机1.3.rgb、depth相机一起标定（效果重复了，但是推荐使用）1.4.取得标定结果1.4.1.得到的标定结果的意义 1.5.IR、RGB相机分别应用标定结果1.5.1.openCV应用标定结果1.5.2.ros…...
常量与变量：编程中重要的两种数据类型
常量与变量 在编程中，我们常常需要存储一些数据。这些数据有些是恒定不变的，有些却是可以随时变化的。对于恒定不变的数据，我们称之为常量；对于可以变化的数据，我们则称之为变量。这两种数据类型在程序中非常重要&…...
( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度：中等 给定一个包含 n 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。 你…...
【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...
武忠祥老师每日一题||定积分基础训练（三）
常用的基本不等式： sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...
Docker安装常用软件-Apollo（有问题）
零：apollo概念介绍 官网网站：GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址：mirrors / ctripcorp / apollo GitCode …...
f(x)与|f(x)|，f ‘ (x)，F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. （因为f(x)在x0的连续点>x0必为|f(x)|的连续点） 注：”[a,b]连续“包括&#…...
今天面了一个来字节要求月薪23K，明显感觉他背了很多面试题...
最近有朋友去字节面试，面试前后进行了20天左右，包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说，80%的人都会栽在第一轮面试，要不是他面试前做足准备，估计都坚持不完后面几轮面试。 其实&…...
如何使用二元三次回归分析建立预测模型？（分析、原理、代码示例）
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型，常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型，其中包括两个自变量（通常…...
面向万物智联的应用框架的思考和探索（上）
原文：面向万物智联的应用框架的思考和探索（上），点击链接查看更多技术内容。 应用框架，是操作系统连接开发者生态，实现用户体验的关键基础设施。其中，开发效率和运行体验是永恒的诉求，…...