快速傅里叶变换FFT学习笔记
点值表示法
我们正常表示一个多项式的方式,形如 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n x n A(x)=a_0+a_1x+a_2x^2+...+a_nx^n A(x)=a0+a1x+a2x2+...+anxn,这是正常人容易看懂的,但是,我们还有一种表示法。
我们知道, n + 1 n+1 n+1个点可以表示出一个 n n n 次的多项式。
于是,我们任意地取 n + 1 n+1 n+1 个不同的值,表示 x x x ,求出的值与 x x x 对应,形成 n + 1 n+1 n+1个点,这就可以表示。
复数
一种表示坐标的方法,对于坐标 ( x , y ) (x,y) (x,y),可写作 x + i y x+iy x+iy,其中 x x x为实部, y y y为虚部。
C++中有复数的模板,complex,可以直接作为变量类型使用。
运算规则,自然不用多说了,也就是直接拿式子算即可。
如果你不会,可以看看百度百科。
我们将点至原点的距离称为模长,将其与原点相连之后与 x x x 轴形成的一个夹角称为辐角,不过呢,对于第三第四象限的点,自然要加上一个 180 ° 180° 180°了。
我的表述自然不够专业,希望可以表述出这个意思吧。
复数的乘法可以理解为,模长相乘,辐角相加。
Tips:
此部分的证明来自 cjx 犇犇。
为啥是这样呢?证明如下:
( a + b i ) ( c + d i ) = a c − b d + i ( b c + a d ) (a+bi)(c+di)=ac-bd+i(bc+ad) (a+bi)(c+di)=ac−bd+i(bc+ad)
那么这个点就是 ( a c − b d , b c + a d ) (ac-bd,bc+ad) (ac−bd,bc+ad),其模长:
( a c − b d ) 2 + ( b c + a d ) 2 = ( a c ) 2 − 2 a b c d + ( b d ) 2 + ( b c ) 2 + 2 a b c d + ( a d ) 2 = ( a c ) 2 + ( b d ) 2 + ( b c ) 2 + ( a d ) 2 = ( a 2 + b 2 ) ( c 2 + d 2 ) \sqrt{(ac-bd)^2+(bc+ad)^2}\\ =\sqrt{(ac)^2-2abcd+(bd)^2+(bc)^2+2abcd+(ad)^2}\\ =\sqrt{(ac)^2+(bd)^2+(bc)^2+(ad)^2}\\ =\sqrt{(a^2+b^2)(c^2+d^2)}\\ (ac−bd)2+(bc+ad)2=(ac)2−2abcd+(bd)2+(bc)2+2abcd+(ad)2=(ac)2+(bd)2+(bc)2+(ad)2=(a2+b2)(c2+d2)
那么我们应该可以看出来这个模长相乘了。
接下来是辐角相加,我们设原来两个辐角为 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2,而模长为 t 1 , t 2 t_1,t_2 t1,t2。
cos ( θ 1 + θ 2 ) = cos ( θ 1 ) cos ( θ 2 ) − sin ( θ 1 ) sin ( θ 2 ) = a t 1 × c t 2 − b t 1 × d t 2 = a c − b d t 1 t 2 \cos(\theta_1+\theta_2)=\cos(\theta_1)\cos(\theta_2)-\sin(\theta_1)\sin(\theta_2)\\ =\frac {a}{t_1}\times\frac {c}{t_2}-\frac {b}{t_1}\times\frac {d}{t_2}\\ =\frac {ac-bd}{t_1t_2} cos(θ1+θ2)=cos(θ1)cos(θ2)−sin(θ1)sin(θ2)=t1a×t2c−t1b×t2d=t1t2ac−bd
我们知道分母是乘积的模长,分子是横坐标,所以这个式子恰好就是乘积辐角对应的 cos \cos cos 值。
那么显然,辐角的值就是 θ 1 + θ 2 \theta_1+\theta_2 θ1+θ2了。
把圆均分
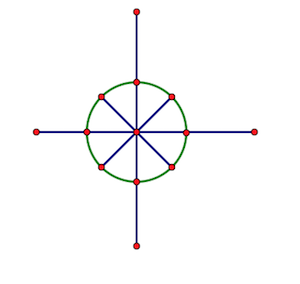
如图是坐标轴上一个以原点为圆心的半径为 1 1 1 的圆。
我们定义 ω n k \omega_n^k ωnk表示从 ( 1 , 0 ) (1,0) (1,0)开始,把圆均分为 n n n份的第 k k k个点的复数,其中 ( 1 , 0 ) (1,0) (1,0)为 ω n 0 \omega_n^0 ωn0。
那么,不难发现, ω n k \omega_n^k ωnk表示的点为 ( cos ( 2 π k n ) , sin ( 2 π n k ) ) (\cos(2\pi\frac k n),\sin(2\pi\frac n k)) (cos(2πnk),sin(2πkn))。
这是为什么呢?我们考虑它的辐角,由于其平分了一整个圆,所以其辐角为 360 k n ° 360\frac k n° 360nk°,转换为弧度后则为 2 π k n 2\pi\frac k n 2πnk,且模长为 1 1 1,利用三角函数易得其坐标了。
简单推推式子不难发现 ( ω n 1 ) k = ω n k (\omega_n^1)^k=\omega_n^k (ωn1)k=ωnk,这是利用了模长相乘,辐角相加,因为模长是 1 1 1 ,怎么乘都是 1 1 1,于是辐角不断叠加,从定义上看是这样的。
- 性质1: ω d n d k = ω n k \omega _{dn}^{dk}=\omega_n^k ωdndk=ωnk,根据定义可证。
- 性质2: ω n k + n 2 = − ω n k \omega _{n}^{k+\frac n 2}=-\omega_n^k ωnk+2n=−ωnk,两点对称。
这个东西有什么用呢?
离散傅里叶变换
离散傅里叶变换(Discrete Fourier Transform,简称DFT)的思想是利用 ω n k \omega_n^k ωnk将一个多项式转为点值表示法。
对于一个多项式 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1} A(x)=a0+a1x+a2x2+...+an−1xn−1,我们按照前文所云,将所有的 ω n k \omega_n^k ωnk作为 x x x 代入。
于是我们得到了 n − 1 n-1 n−1 个点,使用复数形式表示,成为一个数组 ( y 0 , y 1 , y 2 , . . . , y n − 1 ) (y_0,y_1,y_2,...,y_{n-1}) (y0,y1,y2,...,yn−1)的。
这被称为 A ( x ) A(x) A(x) 的傅里叶变换。
傅里叶逆变换
我们再将其作为一个多项式 B ( x ) = y 0 + y 1 x + . . . . + y n − 1 x n − 1 B(x)=y_0+y_1x+....+y_{n-1}x^{n-1} B(x)=y0+y1x+....+yn−1xn−1。
对于这个多项式 B ( x ) B(x) B(x),代入所有的 ω n − k \omega_n^{-k} ωn−k,也就是 ω n k \omega_n^k ωnk的倒数,得到 ( z 0 , z 1 , z 2 , . . . , z n − 1 ) (z_0,z_1,z_2,...,z_{n-1}) (z0,z1,z2,...,zn−1)。
易得:
z k = ∑ i = 0 n − 1 y i ( ω n − k ) i = ∑ i = 0 n − 1 ( ∑ j = 0 n − 1 a j ( ω n i ) j ) ( ω n − k ) i = ∑ j = 0 n − 1 a j ( ω n i ) j ∑ i = 0 n − 1 ( ω n − k ) i = ∑ j = 0 n − 1 a j ( ω n j ) i ∑ i = 0 n − 1 ( ω n − k ) i = ∑ j = 0 n − 1 a j ∑ i = 0 n − 1 ( ω n j − k ) i z_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i \\ =\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^i)^j)(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j(\omega_n^i)^j\sum_{i=0}^{n-1}(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j(\omega_n^j)^i\sum_{i=0}^{n-1}(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}(\omega_n^{j-k})^i\\ zk=i=0∑n−1yi(ωn−k)i=i=0∑n−1(j=0∑n−1aj(ωni)j)(ωn−k)i=j=0∑n−1aj(ωni)ji=0∑n−1(ωn−k)i=j=0∑n−1aj(ωnj)ii=0∑n−1(ωn−k)i=j=0∑n−1aji=0∑n−1(ωnj−k)i
关于后面那个等比数列,若 j = k j=k j=k,可得 1 1 1,否则用等比数列式子可知为 0 0 0。
因此:
z k = n a k a k = z k n z_k=na_k\\ a_k=\frac {z_k} n zk=nakak=nzk
所以我们可以求出原来的多项式了。
有几点需要注意:
- 我们提取 a i a_i ai 只提取实部,因为虚部是虚数,无法经过我们的转换后变成实数。
- 数字有一定误差(毕竟你使用了三角函数等东西,小数是会有误差的),所以要四舍五入。
for(int i=0;i<=len-1;i++)
{ans[i]+=floor(a[i].real()/len+0.5);
}
快速傅里叶变换
快速傅里叶变换(Fast Fourier Transform,简称FFT),是在 DFT的基础上我们发现时间复杂度依然需要 O ( n 2 ) O(n^2) O(n2),没有含金量,所以我们要给他含金量!
我们可以使用分治的思想,使得时间复杂度降至 O ( n log n ) O(n\log n) O(nlogn)。
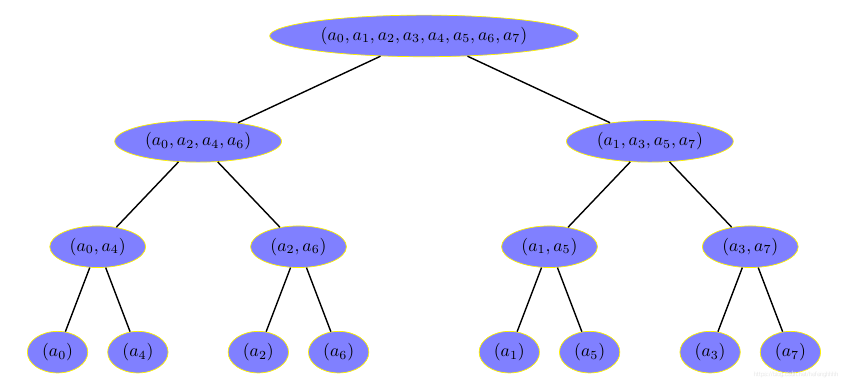
对于 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1} A(x)=a0+a1x+a2x2+...+an−1xn−1,我们可以:
A 1 ( x ) = a 0 + a 2 x + . . . , A 2 ( x ) = a 1 + a 3 x + . . . A ( x ) = A 1 ( x 2 ) + x A 2 ( x 2 ) A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) A_1(x)=a_0+a_2x+...,A_2(x)=a_1+a_3x+...\\ A(x)=A_1(x^2)+xA_2(x^2)\\ A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})\\ A(\omega_n^k)=A_1(\omega_{\frac n 2}^{k})+\omega_n^kA_2(\omega_{\frac n 2}^{k})\\ A1(x)=a0+a2x+...,A2(x)=a1+a3x+...A(x)=A1(x2)+xA2(x2)A(ωnk)=A1(ωn2k)+ωnkA2(ωn2k)A(ωnk)=A1(ω2nk)+ωnkA2(ω2nk)
同理:
A ( ω n k + n 2 ) = A 1 ( ω n 2 k + n ) + ω n k + n 2 A 2 ( ω n 2 k + n ) A ( ω n k + n 2 ) = A 1 ( ω n 2 k ) − ω n k A 2 ( ω n 2 k ) A(\omega_n^{k+\frac n 2})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac n 2}A_2(\omega_n^{2k+n})\\ A(\omega_n^{k+\frac n 2})=A_1(\omega_{\frac n 2}^{k})-\omega_n^{k}A_2(\omega_{\frac n 2}^{k})\\ A(ωnk+2n)=A1(ωn2k+n)+ωnk+2nA2(ωn2k+n)A(ωnk+2n)=A1(ω2nk)−ωnkA2(ω2nk)
不错!利用这两个式子,我们可以在 O ( n log n ) O(n \log n) O(nlogn) 的时间复杂度求出 A ( x ) A(x) A(x)。
不过注意这里一直有一个除二操作,为了方便,我们需要把多项式补成一个次数为 2 x − 1 2^x-1 2x−1 的多项式。
可以写一个递归来求解。
注意这个取倒可以利用共轭复数,对于 a + i b a+ib a+ib,其共轭复数为 a − i b a-ib a−ib。
1 a + i b = a − i b ( a + i b ) ( a − i b ) = a − i b a 2 + b 2 \frac {1}{a+ib}=\frac {a-ib}{(a+ib)(a-ib)}=\frac {a-ib}{a^2+b^2} a+ib1=(a+ib)(a−ib)a−ib=a2+b2a−ib
由于此处 a 2 + b 2 = 1 a^2+b^2=1 a2+b2=1 ,因此其共轭复数为其倒数。
void FFT(cp *a,LL n,bool inv)//inv 表示omega是否取倒
{if(n==1)return;static cp buf[N];LL m=n/2;for(int i=0;i<=m-1;i++)buf[i]=a[2*i],buf[i+m]=a[2*i+1];//奇偶分开for(int i=0;i<=n-1;i++)a[i]=buf[i];FFT(a,m,inv),FFT(a+m,m,inv);for(int i=0;i<=m-1;i++){cp x=omega(n,i);if(inv)x=conj(x);//conj(x)求解共轭复数buf[i]=a[i]+x*a[i+m],buf[i+m]=a[i]-x*a[i+m];}for(int i=0;i<=n-1;i++)a[i]=buf[i];
}
利用FFT求解多项式的乘积
这个还是十分简单的,直接把两个多项式转化为两个长度相同的次数为 2 x − 1 2^x-1 2x−1的多项式。
求解出其傅里叶变换形式之后,对于每个点对应的复数,相乘即可。
为什么呢?
这里有一个误区大家要注意, a i a_i ai 不是一个点,而是单纯因为 ω n i \omega_n^i ωni是一个复数,所以 a i a_i ai 才变成了一个复数, a i a_i ai只是表示 A ( ω n i ) A(\omega_n^i) A(ωni)的值。
首先我们知道当前的 a i a_i ai表示的是 A ( ω n i ) A(\omega_n^i) A(ωni), b i b_i bi表示的是 B ( ω n i ) B(\omega_n^i) B(ωni),那么我们将两个值直接相乘。
因此多项式相乘以后,我们希望 a i = A ( ω n i ) B ( ω n i ) a_i=A(\omega_n^i)B(\omega_n^i) ai=A(ωni)B(ωni),那么就是直接相乘喽。
给一个简单的实现:
nclude<bits/stdc++.h>
#define LL int
#define cp complex<double>
using namespace std;
const double PI=acos(-1.0000);
const int N=5e6+5;
cp omega(LL n, LL k)
{return cp(cos(2*PI*k/n),sin(2*PI*k/n));
}
LL n,x,len,ans[N];
cp a[N],b[N];
//上文的 FFT 实现省去
int main()
{scanf("%d",&n); len=1;while(len<2*n)len*=2;for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x);for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x);FFT(a,len,0),FFT(b,len,0);for(int i=0;i<=len-1;i++)a[i]*=b[i];FFT(a,len,1);for(int i=0;i<=len-1;i++)//进位{ans[i]+=floor(a[i].real()/len+0.5);ans[i+1]+=ans[i]/10;ans[i]%=10;}int i=len;for(i;i>=0&&ans[i]==0;i--);//前导零if(i==-1)len=0;for(;i>=0;i--)printf("%d",ans[i]);
}
非递归FFT
这里有一个优化,我们发现每次递归有一个把 a i a_i ai 奇偶分开的过程,本质来看,就是将二进制末尾为 0 0 0 的数字与二进制末尾为 1 1 1 的数字分开。
我们不妨想一下,对于一个数 x x x,其位置可以根据其二进制确定,就是其二进制倒过来的数字。
我们先将每个 a i a_i ai 放置在对应的位置,然后向上逐渐合并。
void FFT(cp *a,bool inv)
{LL lim=0;while((1<<lim)<len)lim++;for(int i=0;i<=len-1;i++){LL t=0;for(int j=0;j<lim;j++)if((i>>j)&1)t|=(1<<(lim-j-1));//处理其翻转后的值if(i<t)swap(a[i],a[t]);}static cp buf[N];for(int l=2;l<=len;l*=2){LL m=l/2;for(LL j=0;j<=len-1;j+=l){for(LL i=0;i<=m-1;i++){cp x=omega(l,i+j);if(inv)x=conj(x);buf[i+j]=a[i+j]+x*a[i+j+m];buf[i+j+m]=a[i+j]-x*a[i+j+m];}}for(int j=0;j<=len-1;j++)a[j]=buf[j];}
}
蝴蝶操作
这个东西其实就是想了个办法使得把工具人数组 buf 除掉了。
调调顺序即可。
void FFT(cp *a,bool inv)
{LL lim=0;while((1<<lim)<len)lim++;for(int i=0;i<=len-1;i++){LL t=0;for(int j=0;j<lim;j++)if((i>>j)&1)t|=(1<<(lim-j-1));if(i<t)swap(a[i],a[t]);}for(int l=2;l<=len;l*=2){LL m=l/2;for(LL j=0;j<=len-1;j+=l){for(LL i=0;i<=m-1;i++){cp x=omega(l,i+j);if(inv)x=conj(x);x*=a[i+j+m];a[i+j+m]=a[i+j]-x;a[i+j]=a[i+j]+x;}}}
}
一些小优化
对于 i i i 的二进制翻转可以先预处理出来,我们用 R i R_i Ri 表示 i i i 的二进制翻转。
然后 ω n k \omega_n^k ωnk 可以利用性质累乘,会快很多,因为复数的各种操作常数巨大,直接累乘常数较小。
最后代码就长这样了:
#include<bits/stdc++.h>
#define LL int
#define cp complex<double>
using namespace std;
const double PI=acos(-1.0000);
const int N=5e6+5;
cp omega(LL n, LL k)
{return cp(cos(2*PI*k/n),sin(2*PI*k/n));
}
LL n,len,lim,x,ans[N],r[N];
cp a[N],b[N];
void FFT(cp *a,bool inv)
{for(int i=0;i<=len-1;i++){LL t=r[i];if(i<t)swap(a[i],a[t]);}for(int l=2;l<=len;l*=2){LL m=l/2;cp omg=omega(l,1);for(LL j=0;j<=len-1;j+=l){cp x(1,0); for(LL i=0;i<=m-1;i++){cp t=x;if(inv)t=conj(t);t*=a[i+j+m];a[i+j+m]=a[i+j]-t,a[i+j]=a[i+j]+t;x*=omg;}}}
}
int main()
{scanf("%d",&n); len=1;while(len<2*n)len*=2,lim++;for(int i=0;i<=len-1;i++){LL t=0;for(int j=0;j<lim;j++)if((i>>j)&1)t|=(1<<(lim-j-1));r[i]=t;}for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x);for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x);FFT(a,0),FFT(b,0);for(int i=0;i<=len-1;i++)a[i]*=b[i];FFT(a,1);for(int i=0;i<=len-1;i++){ans[i]+=floor(a[i].real()/len+0.5);ans[i+1]+=ans[i]/10;ans[i]%=10;}int i=len;for(i;i>=0&&ans[i]==0;i--);if(i==-1)len=0;for(;i>=0;i--)printf("%d",ans[i]);
}
参考
胡小兔-小学生都能看懂的FFT!!!
相关文章:
快速傅里叶变换FFT学习笔记
点值表示法 我们正常表示一个多项式的方式,形如 A ( x ) a 0 a 1 x a 2 x 2 . . . a n x n A(x)a_0a_1xa_2x^2...a_nx^n A(x)a0a1xa2x2...anxn,这是正常人容易看懂的,但是,我们还有一种表示法。 我们知道…...
如何下载安装驱动
1 打开浏览器 这里以Edge浏览器举例 第一步打开桌面上的Edge浏览器 如果您的桌面上没有 那么找到搜索栏 搜索Edge 然后打开 打开之后一般是这样 然后把我发送您的地址 驱动下载地址 https://t.lenovo.com.cn/yfeyfYyD (这个网址只是一个例子) 删除掉前…...

鸿蒙Hi3861学习四-Huawei LiteOS介绍
一、什么是LitesOS Huawei LiteOS是华为针对物联网领域推出的轻量级物联网操作系统,是华为物联网战略的重要组成部分,具备轻量级、低功耗、互联互通、组件丰富、快速开发等关键能力。基于物联网领域业务特征打造领域性技术栈,为开发者提供“一…...

Vue核心 收集表单数据 过滤器
1.14. 收集表单数据 收集表单数据: 若: ,则v-model收集的是value值,用户输入的就是value值。若: ,则v-model收集的是value值,且要给标签配置value值。若: 没有配置input的value属性,那么收集的就是checked(勾选 or 未…...
华为EC6108V9E/EC6108V9I_rk3228_安卓4.4.4_通刷_卡刷固件包
华为EC6108V9E/EC6108V9I_rk3228_安卓4.4.4_通刷_卡刷固件包-内有教程 特点: 1、适用于对应型号的电视盒子刷机; 2、开放原厂固件屏蔽的市场安装和u盘安装apk; 3、修改dns,三网通用; 4、大量精简内置的…...

数字化转型导师坚鹏:面向数字化转型的大数据顶层设计实践
面向数字化转型的大数据顶层设计实践 课程背景: 数字化背景下,很多企业存在以下问题: 不清楚大数据思维如何建立? 不清楚企业大数据分析方法? 不了解大数据应用成功案例? 课程特色: …...
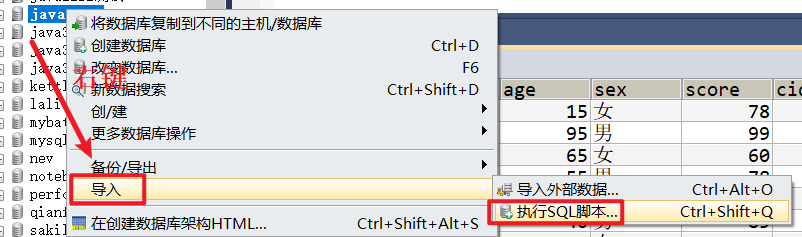
day27_mysql
今日内容 零、 复习昨日 一、单表查询 二、多表联查 零、 复习昨日 1 DDL,DML,DQL是啥 DDL 数据定义语言(库,表,列)DML 数据操作语言(表内数据的操作增删改)DQL 数据查询语言(表内数据的查询&am…...

QwtPlotCurve使用说明
QwtPlotCurve是Qwt库中用于绘制曲线的类,可以在QwtPlot上绘制各种类型的曲线,如折线、样条线、散点等。以下是QwtPlotCurve的一些常用函数和使用说明: setSamples(const QPolygonF &samples):设置曲线的数据点,参数…...
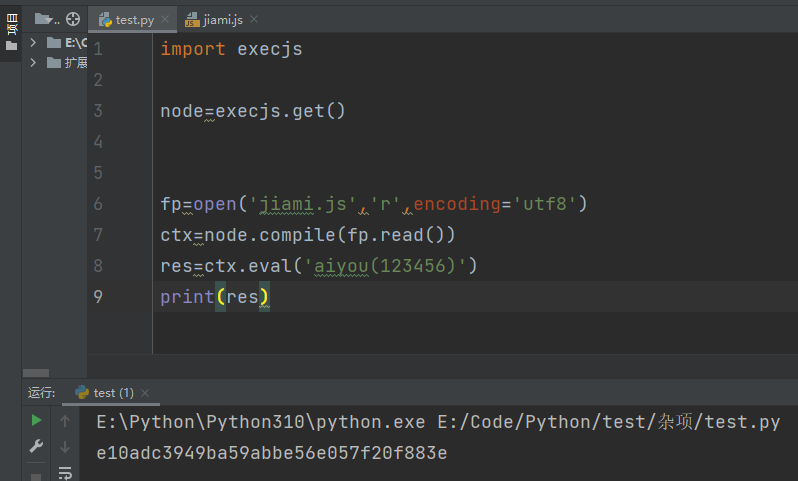
JS逆向 -- 某平台登录加密分析
一、打开网站,使用账号密码登录 账号:aiyou123.com 密码:123456 二、通过F12抓包,抓到如下数据,发现密码加密了 三、加密结果是32位,首先考虑是md5加密。 四、全局搜索pwd,点击右上角…...

一分钟快速实现Flask框架的蓝图和视图
一分钟快速实现Flask框架的蓝图和视图 Flask是一个轻量级的Web应用框架,非常适合快速开发小型的Web应用。Flask框架使用蓝图(Blueprint)和视图(View)的概念来组织应用程序的代码。在本文中,我们将介绍如何…...

Mysql 约束练习【第13章_约束】
#第13章_约束 /* 基础知识 1.1 为什么需要约束? 为了保证数据的完整性! 1.2 什么叫约束?对表中字段的限制。 1.3 约束的分类: 角度1:约束的字段的个数 单列约束 vs 多列约束 角度2:约束的作用范围 列…...

java调用cmd命令
1.首先,我们需要了解一下 java是如何调用 cmd的: 6.在实际的开发中,我们有可能会遇到 java调用 cmd命令的情况: 7.对于一些特定的环境下,例如在嵌入式系统中,那么我们可以使用下面这种方式来调用 cmd命令&a…...

Qt音视频开发36-超时检测和自动重连的设计
一、前言 如果网络环境正常设备正常,视频监控系统一般都是按照正常运行下去,不会出现什么问题,但是实际情况会很不同,奇奇怪怪七七八八的问题都会出现,就比如网络出了问题都有很多情况(交换机故障、网线故障、带宽故障等),所以监控系统在运行过程中,还得做超时检测,…...
Reactor 第九篇 WebFlux重构个人中心,效果显著
1 重构背景 原有的开发人员早已离职,代码细节没人知道,经过了一段时间的维护,发现有以下问题: 个人中心系统的特征就是组装各个业务的接口,输出个人中心业务需要的数据,整个系统调用了几十个第三方业务线的…...
Vben Admin 自学记录 —— Drawer组件的基本使用及练习(持续更新中...)
Drawer 抽屉组件 对 antv 的 drawer 组件进行封装,扩展拖拽,全屏,自适应高度等功能。 Drawer相关使用及概念 练习 —— 在之前table基础上,添加查看功能,点击查看按钮,弹出抽屉显示单条表格数据…...

Android 9.0 根据包名默认授予app悬浮窗权限
1.概述 在9.0的设备开发中,对于在app中授予悬浮窗权限,也是通常用的功能,但在设备产品中预制app,需求要求默认授予悬浮窗权限, 就不需要在app中动态申请悬浮窗权限了,所以就来分析下这个实现这个功能 2.根据包名默认授予app悬浮窗权限的核心类 packages\apps\Settings\s…...
)
Swift中Data,String,[UInt8]的相互转换(6种互相转换)
var dataData() var array[UInt8]() var str"" //Data[UInt8] data.append(10) array[UInt8](data) print(array)//[10] //[UInt8]转Data array[1,2,3,4,5] dataData(array) print(data.count)//5 //Data转String data.removeAll() data.append(contentsOf:[0x31,…...

【微软Bing王炸更新】无需等待,人人可用,答案图文并茂,太牛了
🚀 AI破局先行者 🚀 🌲 AI工具、AI绘图、AI专栏 🍀 🌲 如果你想学到最前沿、最火爆的技术,赶快加入吧✨ 🌲 作者简介:硕风和炜,CSDN-Java领域优质创作者🏆&am…...
腾讯云的cdn怎么配置|腾讯云CDN配置教程
众所周知,WordPress系统不挂加速或者是服务器不好速度贼慢,所以要想办法解决访问速度的问题,经过我不断的研究腾讯云的CDN,因为我用的是zibll子比主题,不懂的就挂会导致无法使用第三方登录,因为有缓存导致一直不回调一直卡在那个登录界面和支付没反应要么出现二维码,要么…...
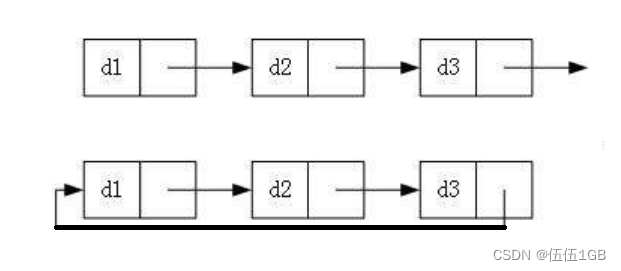
数据结构入门-顺序表链表
线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。线性表是一种实际中广泛使用多个数据结构,常见的线性表:顺序表、链表、栈、队列、字符串... 线性表在逻辑上是线性结构,也就说是连续的一条直线。…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
