C++数据结构:手撕红黑树
目录
一. 红黑树的概念及结构
二. 红黑树节点的定义
三. 红黑树节点的插入
3.1 初步查找插入节点的位置并插入节点
3.2 红黑树结构的调整
3.3 红黑树节点插入完整版代码
四. 红黑树的结构检查
4.1 检查是否为搜索树
4.2 检查节点颜色是否满足要求
附录:红黑树完整版代码
一. 红黑树的概念及结构
在我之前的博客C++数据结构:手撕AVL树_【Shine】光芒的博客-CSDN博客中对AVL树的结构及插入节点操作进行了分析,AVL树要求以每个节点为根节点的子树的左右子树高度差不超过1,以此来保证搜索树查找数据的时间复杂度为O(logN)。
但是,AVL树对高度差的要求过于严格,会导致在插入节点的过程中频繁进行旋转,造成数据插入效率低下。为了权衡插入数据与查找数据的效率,一种新的数据结构 -- 红黑树 被提出。相比于AVL树,红黑树对高度差的要求适当进行了放松,红黑树要求:最长路径的节点数目不超过最短路径的两倍。
红黑树的每个节点为红色或黑色,通过一定的规则控制节点颜色,来达到最长路径节点数目不超过最短路径节点数目两倍的要求,这也是红黑树名称的由来。

一颗结构正确的红黑树,要么为空树,要么满足一下几个条件:
- 每个节点为红色或者黑色。
- 根节点为黑色。
- 如果一个节点为红色,那么它的两个根节点一定为黑色,即:红黑树中没有连续的红色节点,但是,可以有连续的黑色节点。
- 对于每个节点,从该节点到其后代叶子结点的路径上,黑色节点的数目相同,即:每条路径的黑色节点数目相同。
- 叶子节点都为黑色节点。(注意:这里的叶子节点是指NULL节点)
为什么满足上面几条规则就能保证最长路径不超过最短路径两倍?
- 极限最短:一条路径上全为黑色。
- 极限最长:一黑一红间隔排布。
规则4要求每条路径上黑色节点数目相同,那么极限最短路径和极限最长路径肯定具有相同数目的黑色节点,假设每条路径上黑色节点数目为N,那么极限最短路径有N个节点,极限最长路径有2N个节点,这样就满足了红黑树的路径长度的要求。
二. 红黑树节点的定义
红黑树的节点应当被定义为一个三叉链,具有三个红黑树节点指针,分别为:指向左孩子节点的指针_left、指向右孩子节点的指针_right,指向父亲节点的指针_parent。这里存储父亲节点指针的目的是为了在插入数据后检查红黑树结构是否正确以及进行变色及旋转操作。
同时,还应当定义Color枚举常量,使用_col来表示节点颜色,并存储一键值对kv来表示节点数据。
代码2.1:(红黑树节点)
//枚举常量 -- 红色、黑色
enum Color
{RED,BLACK
};//定义红黑树节点
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;std::pair<K, V> _kv; //每个节点存储的键值对Color _col; //节点颜色RBTreeNode(const std::pair<K, V>& kv) //节点构造函数: _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){ }
};三. 红黑树节点的插入
3.1 初步查找插入节点的位置并插入节点
红黑树节点插入位置的查找与普通搜索二叉树和AVL树均一致,流程为:
- 如果当前位置为nullptr,那么该位置为插入节点的位置。
- 如果当前节点值大于要插入的值,到该节点的左子树去查找。
- 如果当前节点值小于要插入的值,到该节点的右子树去查找。
- 如果当前节点值等于要插入的值,则插入失败。(二叉搜索树一般不允许存在相同的节点)。
当查找到插入位置后,判断是插入到了其父亲节点的左孩子位置还是右孩子位置,将新节点与其父亲节点进行连接。
注意:新插入的节点应初步设置为红色。因为:红黑树要求每条路径上黑色节点数目相同,而如果给定新插入的节点为黑色,那么根节点的另一颗没有插入数据的子树中也要想办法增加黑色节点数目或旋转来满足结构要求,这样后期调整红黑树结构就会变得复杂。而初步设定节点为红色,只是有可能存在连续红色节点,只需调整新节点所在子树节点的颜色或进行简单旋转即可。
3.2 红黑树结构的调整
红黑树结构调整主要涉及到四个节点,通过观察下面四个节点的颜色,进行分类讨论,采取不同的方法调整红黑树结构:
- cur节点 -- 新插入的节点。
- p节点 -- 父亲节点,p = cur->_parent。
- g节点 -- 祖父节点,g = p->_parent。
- u节点 -- 叔叔节点,与p具有共同父亲节点的节点。u->_parent = p->_parent = g。
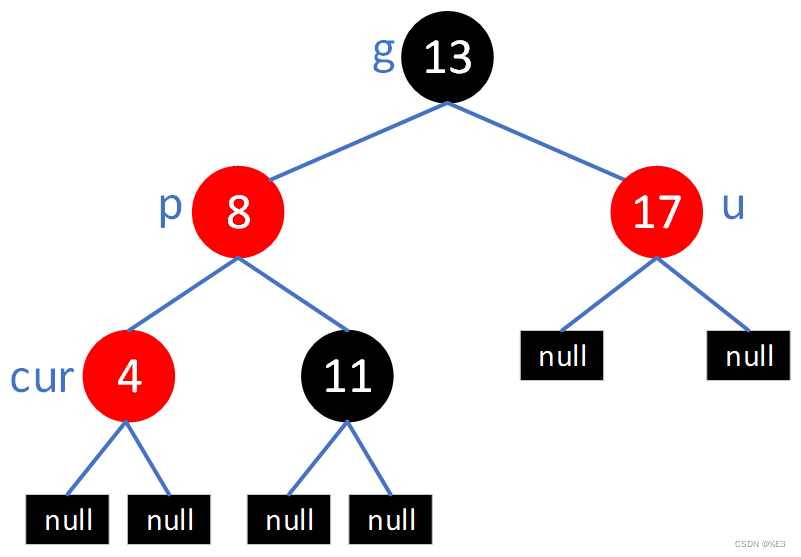
如果p节点为黑色节点,则红黑树已经满足结构要求,不需要再进行调整,如果p节点为红色,那么则会存在连续的红色节点,要进行调整。对于如何调整,分为两大种情况及数种细分情况进行讨论:
- cur为红,p为红,g为黑,u存在且为红。
- cur为红,p为红,g为黑,u不存在或u存在且为黑。
由此可以看出,u的颜色是如何调整的关键所在。
情况一:cur为红,p为红,g为黑,u存在且为红。
将p节点和u节点变为黑色,将g节点变为红色,然后将cur节点更新为g节点,将p节点更新为更新为g->_parent节点,继续向上调整。
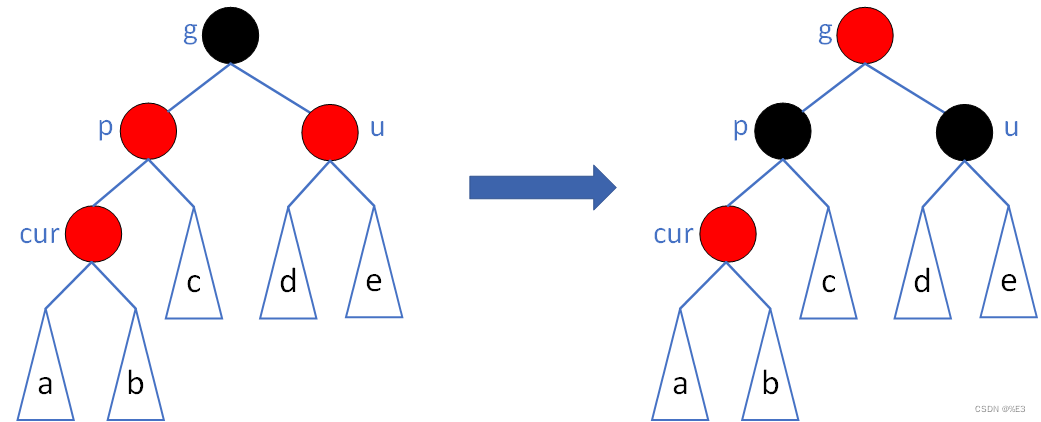
情况二:cur为红,p为红,g为黑,u不存在或u存在且为红。
- 情况2.1:节点cur为p的左子节点,p为g的左子节点 -- 右单旋 + 变色
先对g节点进行右单旋操作,然后将p节点变为黑色,g节点变为红色。

- 情况2.2:节点cur为p的右子节点,p为g的右子节点 -- 左单旋 + 变色
先对g节点进行左单旋操作,然后将p节点变为黑色,g节点变为红色。

- 情况2.3:节点cur为p的右子节点,p为g的左子节点 -- 左右双旋 + 变色
先对p节点进行左单旋,然后对g节点进行右单旋,最后将cur节点变为黑色,将g节点变为红色。
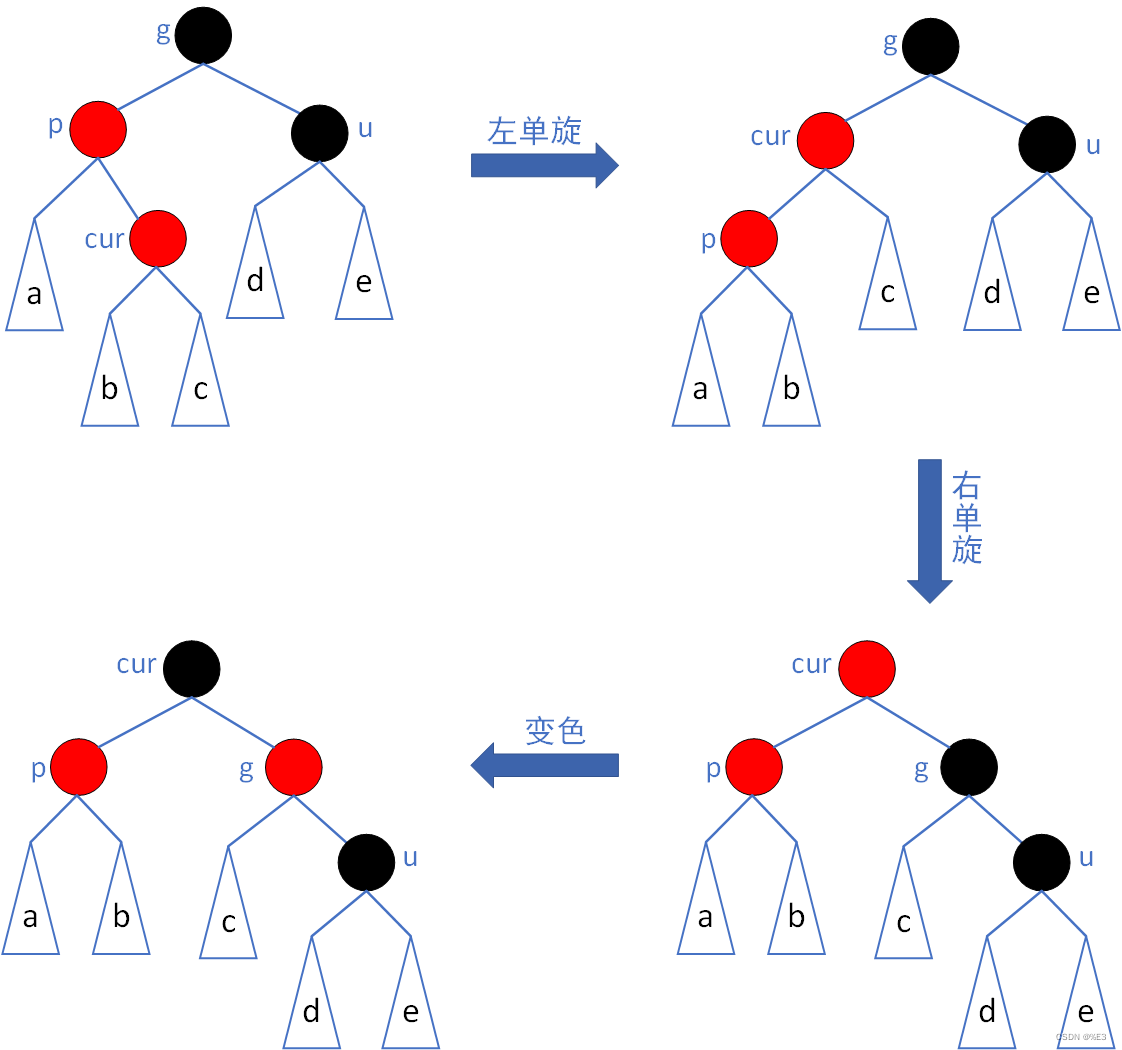
- 情况2.4:节点cur为p的左子节点,节点p为g的右子节点 -- 右左双旋 + 变色
先对p节点进行右单旋,然后对g节点进行左单旋,最后将cur节点变为黑色,将g节点变为红色。

3.3 红黑树节点插入完整版代码
bool insert(const std::pair<K, V>& kv){//插入第一个节点if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK; //根节点为黑色return true;}//寻找节点插入的位置Node* parent = nullptr; Node* cur = _root;while (cur){//如果cur节点的key值大于插入键值对的key,向左子树查找if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if(cur->_kv.first < kv.first) //如果cur节点的key值小于插入键值对的key,向左子树查找{parent = cur;cur = cur->_right;}else //相等表明节点已存在,插入失败{return false;}}//判断新节点是parent的左节点还是右节点,链接//默认新插入的节点为红色cur = new Node(kv);cur->_col = RED;cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}//如果parent节点不为空且为红色,那么红黑树的结构在插入节点后被破坏,需要调整while (parent && parent->_col == RED){Node* grandParent = parent->_parent; //祖父节点assert(grandParent);assert(grandParent->_col == BLACK); //断言检查,如果祖父节点为空或为黑色,那么红黑树结构在节点插入之前就存在问题if (parent == grandParent->_left) //插入在祖父节点的左子树{Node* uncle = grandParent->_right;//情况一:cur为红,parent为红,grandFather为黑,uncle为红if (uncle && uncle->_col == RED){//将parent节点和uncle节点变为黑,grandFather节点变为红,然后继续向上调整parent->_col = BLACK;uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent;} else //情况二、三:cur为红,parent为红,grandFather为黑,uncle不存在或为黑{if (parent->_left == cur){//情况二 -- 进行右单旋 + 变色(parent变黑,grandFather变红)// g// p u//cRotateR(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else{//情况三 -- 进行左右双旋 + 变色(cur节点变为黑,grandFater节点变为红)// g// p u// u RotateLR(grandParent);cur->_col = BLACK;grandParent->_col = RED;}break;}}else //parent == grandParent->_right{Node* uncle = grandParent->_left; //叔叔节点//情况一:cur为红,parent为红,grandFather为黑,uncle为红if (uncle && uncle->_col == RED){//将parent节点和uncle节点变为黑,grandFather节点变为红,然后继续向上调整parent->_col = BLACK;uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent;}else{//情况二、三:cur为红,parent为红,grandFather为黑,uncle不存在或为黑if (parent->_right == cur){//情况二 -- 进行右单旋 + 变色(parent变黑,grandFather变红)// g// u p// cRotateL(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else{//情况三 -- 进行右左双旋 + 变色(cur节点变为黑,grandFater节点变为红)// g// u p// cRotateRL(grandParent);cur->_col = BLACK;grandParent->_col = RED;}break;}}}_root->_col = BLACK; //根节点为黑色return true;}void RotateR(Node* parent) //右单旋函数{Node* pNode = parent->_parent; Node* pL = parent->_left; //左子节点Node* pLR = pL->_right; //左子节点的右子节点//将pLR节点托管给parent节点的左子节点parent->_left = pLR;if (pLR != nullptr){pLR->_parent = parent;}//将父亲节点托管给pL节点的右子节点pL->_right = parent; parent->_parent = pL;//此时这颗进行旋转的子树的根节点变为了pL,pL要与pNode节点连接if (parent == _root){_root = pL;pL->_parent = nullptr;}else{pL->_parent = pNode;if (pNode->_left == parent){pNode->_left = pL;}else{pNode->_right = pL;}}}void RotateL(Node* parent) //左单旋函数{Node* pNode = parent->_parent;Node* pR = parent->_right; //右子节点Node* pRL = pR->_left; //右子节点的左子节点//将pLR节点托管给parent节点的右子节点parent->_right = pRL;if (pRL != nullptr){pRL->_parent = parent;}//将parent节点托管给pR的左子节点pR->_left = parent;parent->_parent = pR;if (_root == parent){_root = pR;_root->_parent = nullptr;}else{pR->_parent = pNode;if (pNode->_left == parent){pNode->_left = pR;}else{pNode->_right = pR;}}}void RotateLR(Node* parent) //左右双旋函数{RotateL(parent->_left);RotateR(parent);}void RotateRL(Node* parent) //右左双旋函数{RotateR(parent->_right);RotateL(parent);}四. 红黑树的结构检查
4.1 检查是否为搜索树
采用中序遍历,得到一串递增的数据即可证明为搜索树。
代码4.1:(中序遍历)
//中序遍历函数void InOrder(){_InOrder(_root);std::cout << std::endl;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);std::cout << root->_kv.first << " ";_InOrder(root->_right);}4.2 检查节点颜色是否满足要求
需要进行以下两个方面的检查:
- 检查每条路径上的黑色节点数量是否相同。
- 检查是否不存在连续的红色节点。
检查每条路径上的黑色节点数目时,可以选取其中一条路径作为基准(一般为最左侧路径或最右侧路径),通过函数遍历每条路径,获取每条路径上的黑色节点数目,与基准路径的黑色节点数目进行比较,如果不相同,则不满足红黑树结构要求。

红黑树要求红色节点的左右孩子节点必须为黑色,但是对孩子节点颜色进行检查较为繁琐,因此,当遇到红色节点时,检查其父亲节点是否为空或者为黑色即可,如果红色节点的父亲节点依旧为红色,则表明树中存在连续的红色节点,不满足红黑树结构要求。
代码4.2:(节点颜色检查)
//红黑树检验函数bool IsRBTree(){//空树是合法的红黑树if (_root == nullptr){return true;}//检查根节点颜色if (_root->_col == RED){std::cout << "根节点颜色不是黑色" << std::endl;}int baseBlackNum = 0; //基准黑色节点个数//以最左侧路径为基准,计算黑色节点个数,每条路径黑色节点数目都应该相同Node* cur = _root;while (cur){if (cur->_col == BLACK){++baseBlackNum;}cur = cur->_left;}bool blackNumTrue = PrevCheck(_root, 0, baseBlackNum); //检查每条路径黑色节点数目是否相同bool colorTrue = CheckColor(_root); //检查是否存在连续红色节点return blackNumTrue && colorTrue;}bool CheckColor(Node* root){if (root == nullptr){return true;}//如果本节点为红色且父亲节点也为红色,证明存在连续红色节点,结构错误if (root->_col == RED && root->_parent && root->_parent->_col == RED){std::cout << "存在连续的红色节点" << std::endl;return false;}return CheckColor(root->_left) && CheckColor(root->_right);}bool PrevCheck(Node* root, int blackNum, int baseBlackNum){if (root == nullptr){if (blackNum != baseBlackNum){std::cout << "每条路径上黑色节点的数目不同" << std::endl;return false;}else{return true;}}if (root->_col == BLACK){++blackNum;}return PrevCheck(root->_left, blackNum, baseBlackNum)&& PrevCheck(root->_right, blackNum, baseBlackNum);}附录:红黑树完整版代码
//枚举常量 -- 红色、黑色
enum Color
{RED,BLACK
};//定义红黑树节点
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;std::pair<K, V> _kv; //每个节点存储的键值对Color _col; //节点颜色RBTreeNode(const std::pair<K, V>& kv) //节点构造函数: _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){ }
};//红黑树类模板
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node; //类型重定义红黑树节点public:bool insert(const std::pair<K, V>& kv){//插入第一个节点if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK; //根节点为黑色return true;}//寻找节点插入的位置Node* parent = nullptr; Node* cur = _root;while (cur){//如果cur节点的key值大于插入键值对的key,向左子树查找if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if(cur->_kv.first < kv.first) //如果cur节点的key值小于插入键值对的key,向左子树查找{parent = cur;cur = cur->_right;}else //相等表明节点已存在,插入失败{return false;}}//判断新节点是parent的左节点还是右节点,链接//默认新插入的节点为红色cur = new Node(kv);cur->_col = RED;cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}//如果parent节点不为空且为红色,那么红黑树的结构在插入节点后被破坏,需要调整while (parent && parent->_col == RED){Node* grandParent = parent->_parent; //祖父节点assert(grandParent);assert(grandParent->_col == BLACK); //断言检查,如果祖父节点为空或为黑色,那么红黑树结构在节点插入之前就存在问题if (parent == grandParent->_left) //插入在祖父节点的左子树{Node* uncle = grandParent->_right;//情况一:cur为红,parent为红,grandFather为黑,uncle为红if (uncle && uncle->_col == RED){//将parent节点和uncle节点变为黑,grandFather节点变为红,然后继续向上调整parent->_col = BLACK;uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent;} else //情况二、三:cur为红,parent为红,grandFather为黑,uncle不存在或为黑{if (parent->_left == cur){//情况二 -- 进行右单旋 + 变色(parent变黑,grandFather变红)// g// p u//cRotateR(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else{//情况三 -- 进行左右双旋 + 变色(cur节点变为黑,grandFater节点变为红)// g// p u// u RotateLR(grandParent);cur->_col = BLACK;grandParent->_col = RED;}break;}}else //parent == grandParent->_right{Node* uncle = grandParent->_left; //叔叔节点//情况一:cur为红,parent为红,grandFather为黑,uncle为红if (uncle && uncle->_col == RED){//将parent节点和uncle节点变为黑,grandFather节点变为红,然后继续向上调整parent->_col = BLACK;uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent;}else{//情况二、三:cur为红,parent为红,grandFather为黑,uncle不存在或为黑if (parent->_right == cur){//情况二 -- 进行右单旋 + 变色(parent变黑,grandFather变红)// g// u p// cRotateL(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else{//情况三 -- 进行右左双旋 + 变色(cur节点变为黑,grandFater节点变为红)// g// u p// cRotateRL(grandParent);cur->_col = BLACK;grandParent->_col = RED;}break;}}}_root->_col = BLACK; //根节点为黑色return true;}//中序遍历函数void InOrder(){_InOrder(_root);std::cout << std::endl;}//红黑树检验函数bool IsRBTree(){//空树是合法的红黑树if (_root == nullptr){return true;}//检查根节点颜色if (_root->_col == RED){std::cout << "根节点颜色不是黑色" << std::endl;}int baseBlackNum = 0; //基准黑色节点个数//以最左侧路径为基准,计算黑色节点个数,每条路径黑色节点数目都应该相同Node* cur = _root;while (cur){if (cur->_col == BLACK){++baseBlackNum;}cur = cur->_left;}bool blackNumTrue = PrevCheck(_root, 0, baseBlackNum); //检查每条路径黑色节点数目是否相同bool colorTrue = CheckColor(_root); //检查是否存在连续红色节点return blackNumTrue && colorTrue;}private:bool CheckColor(Node* root){if (root == nullptr){return true;}//如果本节点为红色且父亲节点也为红色,证明存在连续红色节点,结构错误if (root->_col == RED && root->_parent && root->_parent->_col == RED){std::cout << "存在连续的红色节点" << std::endl;return false;}return CheckColor(root->_left) && CheckColor(root->_right);}bool PrevCheck(Node* root, int blackNum, int baseBlackNum){if (root == nullptr){if (blackNum != baseBlackNum){std::cout << "每条路径上黑色节点的数目不同" << std::endl;return false;}else{return true;}}if (root->_col == BLACK){++blackNum;}return PrevCheck(root->_left, blackNum, baseBlackNum)&& PrevCheck(root->_right, blackNum, baseBlackNum);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);std::cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateR(Node* parent) //右单旋函数{Node* pNode = parent->_parent; Node* pL = parent->_left; //左子节点Node* pLR = pL->_right; //左子节点的右子节点//将pLR节点托管给parent节点的左子节点parent->_left = pLR;if (pLR != nullptr){pLR->_parent = parent;}//将父亲节点托管给pL节点的右子节点pL->_right = parent; parent->_parent = pL;//此时这颗进行旋转的子树的根节点变为了pL,pL要与pNode节点连接if (parent == _root){_root = pL;pL->_parent = nullptr;}else{pL->_parent = pNode;if (pNode->_left == parent){pNode->_left = pL;}else{pNode->_right = pL;}}}void RotateL(Node* parent) //左单旋函数{Node* pNode = parent->_parent;Node* pR = parent->_right; //右子节点Node* pRL = pR->_left; //右子节点的左子节点//将pLR节点托管给parent节点的右子节点parent->_right = pRL;if (pRL != nullptr){pRL->_parent = parent;}//将parent节点托管给pR的左子节点pR->_left = parent;parent->_parent = pR;if (_root == parent){_root = pR;_root->_parent = nullptr;}else{pR->_parent = pNode;if (pNode->_left == parent){pNode->_left = pR;}else{pNode->_right = pR;}}}void RotateLR(Node* parent) //左右双旋函数{RotateL(parent->_left);RotateR(parent);}void RotateRL(Node* parent) //右左双旋函数{RotateR(parent->_right);RotateL(parent);}private:Node* _root = nullptr;
};相关文章:

C++数据结构:手撕红黑树
目录 一. 红黑树的概念及结构 二. 红黑树节点的定义 三. 红黑树节点的插入 3.1 初步查找插入节点的位置并插入节点 3.2 红黑树结构的调整 3.3 红黑树节点插入完整版代码 四. 红黑树的结构检查 4.1 检查是否为搜索树 4.2 检查节点颜色是否满足要求 附录:红黑…...

Spring IoC 深度学习
Io回顾 IoC 是 Inversion of Control 的简写,译为“控制反转”,它不是一门技术,而是一种设计思想,是一个重要的面向对象编程法则,能够指导我们如何设计出松耦合、更优良的程序。 Spring 通过 IoC 容器来管理所有 Jav…...
C语言从入门到精通第17天(指针和数组联用)
指针和数组联用 不同类型指针变量之间的区别数组的指针指针数组 不同类型指针变量之间的区别 在了解数组和指针联用之前,我们先对指针变量进行补充。我们对比一下int *p1和char *p2的区别? 相同点: 都是指针变量都是用来保存一个内存地址编…...

Android9.0 原生系统SystemUI下拉状态栏和通知栏视图之锁屏通知布局
1.前言 在9.0的系统rom定制化开发中,对于系统原生systemui的锁屏界面的功能也是非常重要的,所以在锁屏页面布局中,也是有通知栏布局的,所以接下来对于息屏亮屏 通知栏布局的相关流程分析,看下亮屏后锁屏页面做了哪些功能 2.原生系统SystemUI下拉状态栏和通知栏视图之锁…...

音视频八股文(10)-- mp4结构
介绍 mp4⽂件格式⼜被称为MPEG-4 Part 14,出⾃MPEG-4标准第14部分 。它是⼀种多媒体格式容器,⼴泛⽤于包装视频和⾳频数据流、海报、字幕和元数据等。(顺便⼀提,⽬前流⾏的视频编码格式AVC/H264 定义在MPEG-4 Part 10)…...
)
python算法中的深度学习算法之深度信念网络(详解)
目录 学习目标: 学习内容: 深度信念网络 Ⅰ. 预训练 Ⅱ. 微调 学习目标: 一分钟掌握 python算法中的深度学习算法之深度信念网络 入门知识...
SPSS如何绘制常用统计图之案例实训?
文章目录 0.引言1.绘制简单条形图2.绘制分类条形图3.绘制分段条形图4.绘制简单线图5.绘制多重线图6.绘制垂直线图7.绘制简单面积图8.绘制堆积面积图9.绘制饼图10.绘制直方图11.绘制简单散点图12.绘制重叠散点图13.绘制矩阵散点图14.绘制三维散点图15.绘制简单箱图16.绘制分类箱…...

打动人心的故事 | 如何利用文案在Facebook上塑造品牌形象
在当今的数字营销时代,文案已经成为各大平台上不可或缺的元素之一。在Facebook上,一个好的文案能够为品牌带来巨大的曝光率和用户黏性,甚至可以改变用户对品牌的看法。那么,如何利用文案在Facebook上打动人心,塑造品牌…...

什么是模糊控制?
模糊控制设计原理 1、传统控制系统和模糊控制系统 传统控制系统结构: 控制目的:通过控制器调节控制信号u,使输出信号y达到要求 模糊控制系统结构: 与传统控制系统的差异:用模糊控制器FC(Fuzzy Controller&…...

仿抖音开发需要注意的问题
一、版权问题 仿抖音开发需要注意版权问题,包括内容的版权和软件的版权。在开发的过程中,不要直接抄袭他人的作品,应该注重保护知识产权。 二、安全性问题 仿抖音开发需要重视应用的安全性问题,避免应用在使用过程中发生安全漏…...
如何根据期刊缩写查找期刊?
英文论文写作中,经常会插入参考文献。参考文献中的期刊名称,时常需要使用缩写。或者是手头有期刊缩写后的名称,但是有时候,查了半天也查不到期刊期刊全称,费时费力让人崩溃。今天就给各位学者老师总结一些查询期刊缩写…...
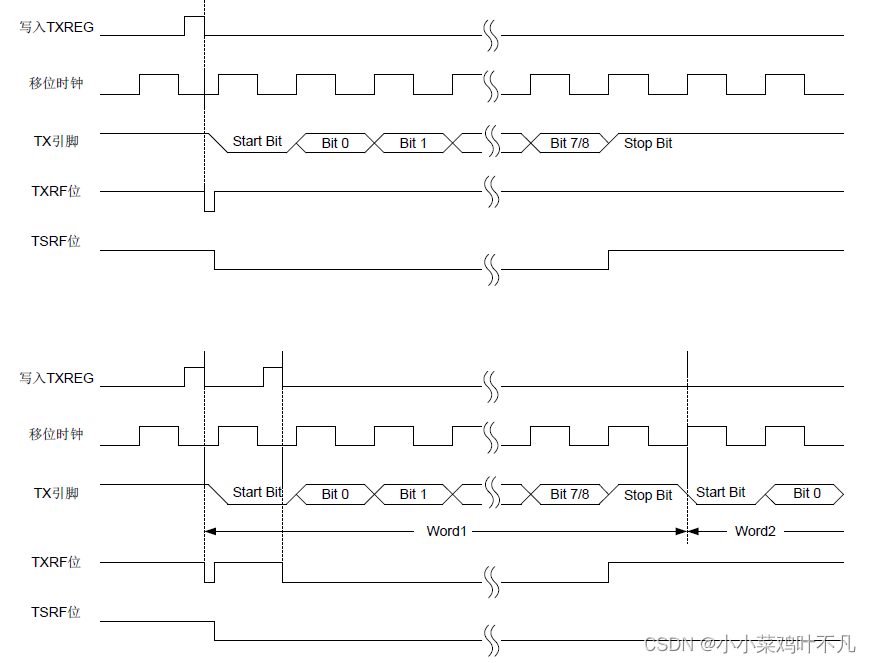
数据发送流程
在发送模式下,UART 的串行数据发送电路主要包括一个发送移位寄存器(TSR),TSR 功能是将数据 逐个移位送出。待发数据必须先写到发送缓冲区中。 TXIFx 是发送中断标志位,可配置为发送缓冲区空或TSR 空。 数据的发送支持7bit 、8bit 或9bit 数据…...

堆及其应用
堆是一种基于树结构的数据结构,通常用于实现优先队列。堆分为最大堆和最小堆两种类型,最大堆的每个节点的值都大于等于其子节点的值,最小堆则相反,每个节点的值都小于等于其子节点的值。 基础算法操作包括: 1. 插入元…...

MySQL数据库备份脚本
PS:此脚本简单易懂,根据实际情况修改个别参数测试后即可使用,如有错误请指出! 1.MySQL数据库备份脚本 #!/bin/bashuser pw ip dateYdate "%Y" date2date "%Y%m%d" date3date "%Y%m%d %H:%M" date…...
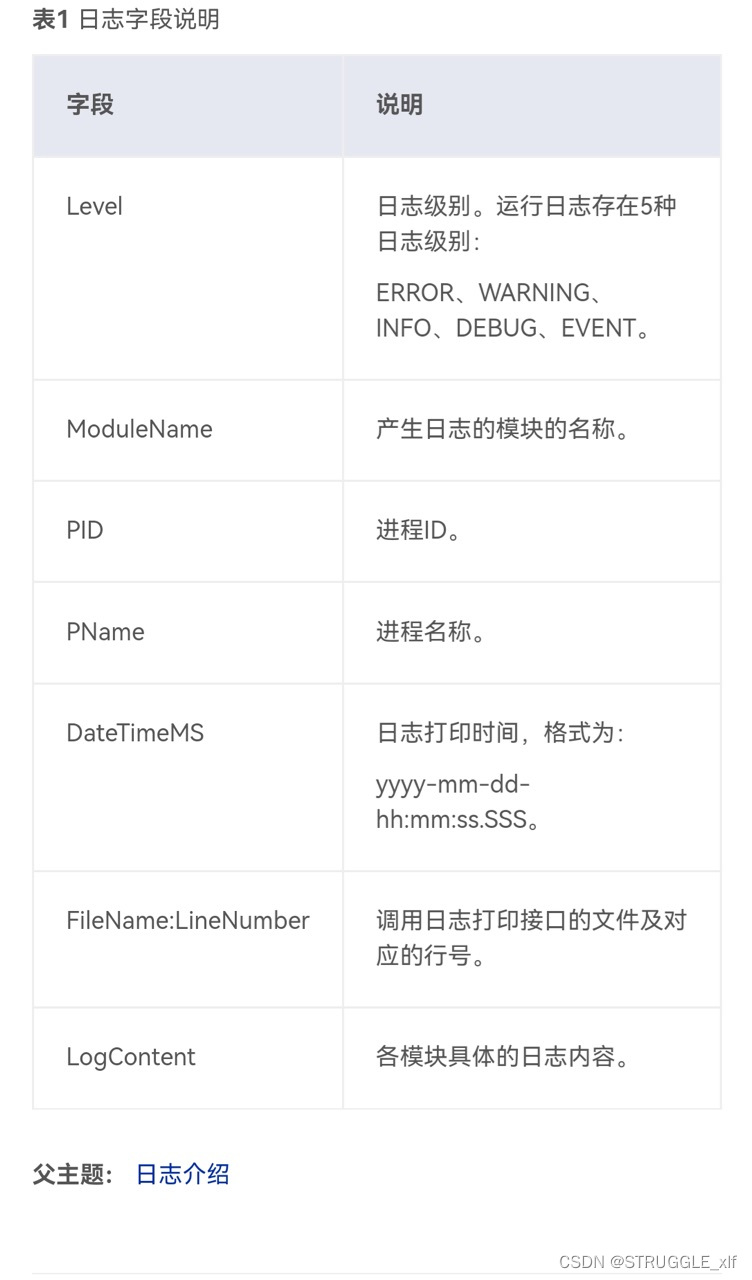
【2023 · CANN训练营第一季】应用开发深入讲解——第三章应用调试
学习资源 日志参考文档 应用开发FAQ 日志主要用于记录系统的运行过程及异常信息,帮助快速定位系统运行过程中出现的问题以及开发过程中的程序调试问题。 日志分为如下两大类: 系统类日志:系统运行产生的日志。主要包括: Contro…...
黎曼几何与黎曼流形
目录 0.黎曼几何 1. 欧几里得几何与黎曼几何的区别 2.黎曼流形 3.黎曼距离 4.切空间 5.黎曼均值 6. SPD矩阵如何形成黎曼流型 7.切线空间映射 8.同余变换和同余不变 9.黎曼对齐 科普性笔记,做了解,不深入。 0.黎曼几何 黎曼几何是一种基于欧几…...

lua | 运算符与字符串
目录 一、运算符 算数运算符 关系运算符 逻辑运算符 其他运算符 运算符优先级 二、字符串 转义字符 方法与用途 字符串截取 字符串大小转换 字符串查找与反转 字符串格式化 字符与整数的转换 匹配模式 本文章为笔者学习分享 学习网站:Lua 基本语法 | …...

NetBackup 10.2 新功能介绍:PostgreSQL 和 MySQL 自动化恢复达成
NetBackup 10.2 新功能介绍:PostgreSQL 和 MySQL 自动化恢复达成 原文来自:VERITAS 中文社区 2023-04-27 在执行恢复任务时,手动提取、更新数据库和实例并将其附加到 PostgreSQL 和 MySQL 是常规操作。而在最新的 NetBackup 10.2 版本中&am…...
ADRV9002官方例程开发过程中遇到的问题
开发环境:Vivado2021.2 HDL版本:hdl_2021_r2 GitHub - analogdevicesinc/hdl at hdl_2021_r2 no-OS版本:no_OS-2021_R2 GitHub - analogdevicesinc/no-OS at 2021_R2 (PS:也可以用Vivado2019.1开发,…...
Figma转换为sketch,分享这3款工具
在我们的设计工作中,我们经常会遇到各种各样的设计文件相互转换的问题。 你经常为此头疼吗?当你遇到Figma转换Sketch文件的问题时,你是如何解决的?Figma转换Sketch文件有工具吗? 根据众多设计师的经验,本…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
