黎曼几何与黎曼流形
目录
0.黎曼几何
1. 欧几里得几何与黎曼几何的区别
2.黎曼流形
3.黎曼距离
4.切空间
5.黎曼均值
6. SPD矩阵如何形成黎曼流型
7.切线空间映射
8.同余变换和同余不变
9.黎曼对齐
科普性笔记,做了解,不深入。
0.黎曼几何
黎曼几何是一种基于欧几里得几何的扩展,它允许在弯曲的空间中研究几何学。黎曼几何被广泛应用于物理学、天文学、地理学、计算机科学、机器学习等领域。
在欧几里得几何中,平面上的直线是直的,而在黎曼几何中,我们允许空间中的直线是弯曲的。这种弯曲通常是由物理现象引起的,例如地球表面的曲率。
在黎曼几何中,我们可以通过定义度量来描述空间的几何结构。度量是一个函数,它测量两个点之间的距离。在欧几里得几何中,度量是标准的欧几里得距离公式,而在黎曼几何中,度量可以是一般的函数形式。黎曼度量通常定义为一个对称的正定二次型。
另外,在黎曼几何中,我们可以定义曲率来描述空间的弯曲程度。曲率度量了一个曲面的局部弯曲程度,并反映了这个曲面相对于欧几里得空间的扭曲程度。在欧几里得空间中,曲率为零,而在弯曲的空间中,曲率可以是正的、负的或零。曲率在物理学中是一个非常重要的概念,因为它描述了引力的强度和方向。
总之,黎曼几何是一种非常重要的数学分支,它扩展了我们对几何学的理解,允许我们在弯曲的空间中研究几何学,并且被广泛应用于物理学、天文学、地理学、计算机科学、机器学习等领域。
1. 欧几里得几何与黎曼几何的区别
欧几里得几何和黎曼几何是两种不同的几何学体系,它们之间的区别主要在于它们所描述的空间的性质和度量方式。
欧几里得几何是在欧氏空间中研究点、线、面及其之间关系的几何学分支,欧氏空间是一个以点、直线、平面为基本元素的空间,满足欧几里得公设。欧几里得几何的基本性质是平行公设,即给定一直线和一个点,可以在该直线上唯一确定一条与该直线平行的直线。
黎曼几何是一种更为广义的几何学,它研究的空间不一定满足欧几里得公设,而是由一个叫做度量的概念所描述的空间。在黎曼几何中,空间被看作是由一个叫做度量张量的对象所描述的,它可以用来测量空间中点之间的距离和角度。与欧几里得几何不同的是,在黎曼几何中,平行公设不再成立,而是被一个叫做测地线的概念所取代。测地线是空间中一条“最短”的路径,它不一定是直线,而是根据度量张量而定的曲线。
简单来说,欧几里得几何研究的是欧氏空间中的几何性质,主要考虑点、线、面之间的关系以及它们之间的距离和角度;而黎曼几何则研究更为广义的空间,在这样的空间中可以有不同于欧氏空间的几何性质,它所考虑的是空间中点之间的距离和角度等度量概念,也涉及到测地线等特殊的几何概念。
2.黎曼流形
黎曼流形是一种数学概念,它描述了一种多维空间的结构,可以用来研究曲线、曲面、流形等几何对象的性质。
具体来说,黎曼流形是一个具有度量的连续空间,这个度量允许我们度量流形上的长度、角度和体积等几何性质。黎曼流形的度量可以用来定义距离、曲率、体积等概念,这些概念对于研究流形上的几何问题非常重要。
黎曼流形的研究在数学上有广泛的应用,尤其在数学物理中。它被用来描述广义相对论中的时空结构,也被用来研究其他物理学问题,例如弦理论、统计力学和量子场论等。除此之外,黎曼流形还在计算机科学中有着广泛的应用,例如计算机视觉、机器学习和图形学等领域。
3.黎曼距离
黎曼距离是定义在黎曼流形上的一种距离度量。对于两个流形上的点,它们之间的黎曼距离
定义为连接它们的最短测地线(geodesic)的长度。
在黎曼流形上,测地线相当于直线的概念,是两点间最短的连线。黎曼距离的定义利用了这个概念,也就是连接两点的最短路径。
黎曼距离在很多数学和工程应用中都有广泛的应用,例如:
-
机器学习和数据分析中的度量学习:在许多数据分析问题中,我们需要寻找一种距离度量,用来衡量数据点之间的相似性。在许多高维数据集中,数据点往往具有复杂的流形结构,此时黎曼距离可以用来描述它们之间的相似性。
-
图像处理和计算机视觉中的形状比较:在形状比较问题中,我们需要比较两个对象的形状相似性。例如,在人脸识别中,我们需要比较两个人脸的形状相似性。此时,可以将人脸表示为一个黎曼流形,利用黎曼距离来比较它们之间的相似性。
-
优化算法中的约束条件:在一些优化问题中,我们需要考虑一些特定的约束条件,例如正定性、旋转不变性等。此时,可以将优化问题定义在一个黎曼流形上,并利用黎曼距离来定义约束条件。
总之,黎曼距离是一种非常重要的距离度量,在许多领域都有着广泛的应用。
4.切空间
在微积分和微分几何中,切空间是一种描述流形上点的局部线性结构的概念。对于一个维流形上的点
,它的切空间可以被视为该点附近的所有局部线性变化的集合。在每个点
处,切空间都是一个
维向量空间,它与欧几里得空间中的向量空间类似,但是它具有更加复杂的拓扑和几何结构。
切空间在微分几何中有着重要的应用。它可以被用来定义曲面的法向量、测地线、曲率等几何量,并且可以被用来描述一些曲面的性质,例如最大和最小曲率的值、曲面的局部形状等。此外,在机器学习和数据分析中,切空间也有着广泛的应用。例如,我们可以将一些高维数据点表示为流形上的点,并利用切空间来描述它们的局部几何结构,从而设计更加复杂的数据分析算法。
对于黎曼流形,切空间也具有重要的作用。由于黎曼流形上每个点的切空间是一个线性空间,我们可以利用它来定义各种线性运算和度量,例如内积、范数、平均值等。这些概念可以被用来构建各种机器学习和优化算法,用于处理具有黎曼流形结构的数据集。
5.黎曼均值
在黎曼流形上,我们可以定义一组数据点的均值,称为黎曼均值(Riemannian mean)或黎曼中心(Riemannian centroid)。黎曼均值是一组数据点在黎曼流形上的中心点,它可以被视为一组数据点的代表点。
在欧几里得空间中,均值可以通过简单地求平均值来计算。但是,在黎曼流形中,由于每个点的切空间是一个不同的线性空间,因此不能直接对坐标求平均值来计算均值。相反,我们需要通过一些特定的算法来计算黎曼均值。
黎曼均值的计算对许多数据分析和机器学习问题非常重要,例如聚类、分类和降维等。例如,在图像处理和计算机视觉中,我们经常需要对一组图像进行处理和分析,此时可以利用黎曼均值来计算这些图像的平均形状和特征。
除了黎曼均值之外,黎曼流形上还有许多其他的统计量和运算,例如黎曼方差、黎曼中心散步矩阵等。这些概念可以被用于构建更加复杂的统计模型和算法,用来处理具有流形结构的数据集。
在黎曼流形上,计算均值的方法不同于欧几里得空间中简单的求平均值。在黎曼流形上,我们可以使用迭代算法来计算均值。以下是一种常见的迭代算法,称为Riemannian Trust-Region (RTR) 方法:
-
初始化:选择任意一个数据点作为起始点
,并选择一个初始的半径
。
-
迭代:对于每个迭代步骤k,进行以下操作:
a. 计算所有数据点与当前点
之间的距离,使用黎曼度量来度量距离。
b. 将距离转化为权重,权重值为距离的倒数的平方。
c. 使用加权平均法计算一个新的均值
,其中每个数据点的权重是在上一步中计算的权重。
d. 计算当前点
与新均值
之间的距离
,使用黎曼度量来度量距离。
e. 如果
小于半径
,则接受新的均值
,并将半径更新为
;否则,拒绝新的均值
,并将半径更新为
f. 重复步骤b-e,直到收敛到一个稳定的均值p。
这种方法是一种基于迭代的局部搜索算法,它通过逐步改进均值来找到一组数据点的黎曼均值。由于黎曼流形上的度量是非线性的,因此这种方法需要进行多次迭代才能收敛到稳定的均值。此外,为了保证算法的收敛性和数值稳定性,需要进行一些额外的约束和调整,例如限制迭代步数、控制半径的大小、避免出现数值不稳定等。
除了RTR方法之外,还有许多其他的方法可以用来计算黎曼均值,例如黎曼梯度下降法、黎曼牛顿法、黎曼平均值算法等。
6. SPD矩阵如何形成黎曼流型
SPD(Symmetric Positive Definite)矩阵是指对称正定矩阵。
一个n阶对称正定矩阵的集合可以表示为。对于任意的
和
,定义如下映射:
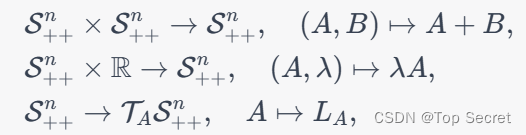
其中是一个从
到
的映射。这个映射定义了一个切空间
,它在每个点
上都是一个
维的向量空间。
接下来,我们定义一个内积在每个切空间
上:
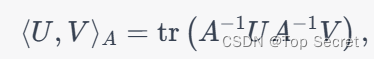
其中。这个内积定义了一个黎曼度量,使得
成为了一个黎曼流形。
需要注意的是,这个黎曼度量是依赖于矩阵A的。也就是说,在上的不同点处,黎曼度量会有所不同。这个事实反映了黎曼流形的一般性质,即流形上的度量可以随着位置而变化。
总之,SPD矩阵上定义的内积和流形结构是如此定义的:首先定义一个切空间,然后定义一个内积,最终得到了一个黎曼流形。
7.切线空间映射
切线空间映射是一种将高维流形中的点映射到其切空间上的方法,通常也称为切映射或切空间投影。
首先,切线空间是指流形上某一点处的切向量所构成的线性空间,也就是该点处的切空间。在微积分中,切向量是描述曲线在该点附近的切线方向的概念。在高维流形上,切向量可以被看作是描述流形在该点处切平面上的切向量。
切线空间映射将一个流形上的点映射到该点处的切空间上,其具体实现方式通常涉及到微积分和线性代数中的概念。在欧几里得空间中,我们可以通过求取该点处的导数或者 Jacobian 矩阵来计算该点处的切空间映射。在黎曼几何中,我们需要借助度量张量来定义切向量,并利用切向量的内积和度量张量来定义切空间的结构。
切线空间映射在机器学习和计算机视觉中有广泛的应用。例如,在流形学习中,切线空间映射可以用来将高维数据嵌入到低维流形中,以便进行数据降维和可视化。在计算机视觉中,切线空间映射可以用来计算图像的梯度和特征,以实现图像分割、目标检测等任务。此外,切线空间映射还可以用来计算流形上的平均值、中心点和曲线等几何概念,以便对流形数据进行聚类和分类。
8.同余变换和同余不变
在黎曼几何中,同余变换指的是保持度量不变的变换。也就是说,给定一个黎曼空间 和一个同余变换
,则对于该空间中任意两点
,有
,其中
是使用度量张量 g 计算的两点之间的距离。
同余变换是黎曼几何中的一个重要性质,它保证了黎曼空间的几何结构在同余变换下不会改变。这一性质可以帮助我们理解和比较不同的黎曼空间,并将它们之间的几何性质进行比较和分类。
同余不变是指同余变换下不变的量,通常包括黎曼曲率张量、黎曼体积元、黎曼联络等。这些量在同余变换下具有不变性,也就是说,它们的值在同余变换下保持不变。同余不变性质是黎曼几何中的一个重要性质,它使得我们能够对黎曼流形进行刻画和比较,并在实际应用中使用黎曼几何的工具和技术。
黎曼空间中的同余变换和同余不变性质在计算机视觉和机器学习中有广泛的应用。例如,在计算机视觉中,同余变换可以用来生成对抗样本和数据增强,以提高深度学习模型的鲁棒性和泛化性能。同余不变性质则可以用来设计具有旋转、平移和缩放不变性的特征和模型,以便在处理自然图像和视频数据时获得更好的性能和效果。
9.黎曼对齐
黎曼对齐(Riemannian alignment)是一种基于黎曼几何的数据对齐方法,它可以将数据点从一个黎曼流形变换到另一个黎曼流形,以便进行比较和分析。
黎曼对齐的主要思想是将数据点从一个流形映射到另一个流形,使得它们在新流形上的位置和结构尽可能相似。具体来说,黎曼对齐分为两个步骤:
-
流形配准(Manifold Registration):将待配准的两个黎曼流形中的一些点对应起来,以便进行对齐。这一步通常使用一些特定的算法来实现,例如基于距离度量的配准方法、基于特征的配准方法、基于变形模型的配准方法等。
-
流形变换(Manifold Transformation):利用配准结果将待对齐的数据点从一个流形变换到另一个流形。在黎曼几何中,流形变换通常使用黎曼流形上的切空间或切空间的扩展来实现。具体来说,可以使用切空间中的切向量和黎曼流形上的黎曼联络来定义流形变换的方向和大小。
黎曼对齐在计算机视觉、机器学习和图像处理等领域中有广泛的应用,例如人脸识别、图像对齐、形状分析、变形建模等。它能够有效地处理具有非欧几里得结构的数据,并且可以提高数据分析的准确性和可靠性。
相关文章:
黎曼几何与黎曼流形
目录 0.黎曼几何 1. 欧几里得几何与黎曼几何的区别 2.黎曼流形 3.黎曼距离 4.切空间 5.黎曼均值 6. SPD矩阵如何形成黎曼流型 7.切线空间映射 8.同余变换和同余不变 9.黎曼对齐 科普性笔记,做了解,不深入。 0.黎曼几何 黎曼几何是一种基于欧几…...

lua | 运算符与字符串
目录 一、运算符 算数运算符 关系运算符 逻辑运算符 其他运算符 运算符优先级 二、字符串 转义字符 方法与用途 字符串截取 字符串大小转换 字符串查找与反转 字符串格式化 字符与整数的转换 匹配模式 本文章为笔者学习分享 学习网站:Lua 基本语法 | …...

NetBackup 10.2 新功能介绍:PostgreSQL 和 MySQL 自动化恢复达成
NetBackup 10.2 新功能介绍:PostgreSQL 和 MySQL 自动化恢复达成 原文来自:VERITAS 中文社区 2023-04-27 在执行恢复任务时,手动提取、更新数据库和实例并将其附加到 PostgreSQL 和 MySQL 是常规操作。而在最新的 NetBackup 10.2 版本中&am…...
ADRV9002官方例程开发过程中遇到的问题
开发环境:Vivado2021.2 HDL版本:hdl_2021_r2 GitHub - analogdevicesinc/hdl at hdl_2021_r2 no-OS版本:no_OS-2021_R2 GitHub - analogdevicesinc/no-OS at 2021_R2 (PS:也可以用Vivado2019.1开发,…...
Figma转换为sketch,分享这3款工具
在我们的设计工作中,我们经常会遇到各种各样的设计文件相互转换的问题。 你经常为此头疼吗?当你遇到Figma转换Sketch文件的问题时,你是如何解决的?Figma转换Sketch文件有工具吗? 根据众多设计师的经验,本…...

淘宝天猫1688京东商品详情API接口,封装接口可高并发
要提供商品详情数据需要知道具体的商品信息,但通常商品详情数据应包括以下内容: 商品名称:商品的名称,以方便顾客对其进行识别和区分。 商品描述:一段让顾客能够全面认识商品的描述。应能够有效地展示商品的特性、功能…...
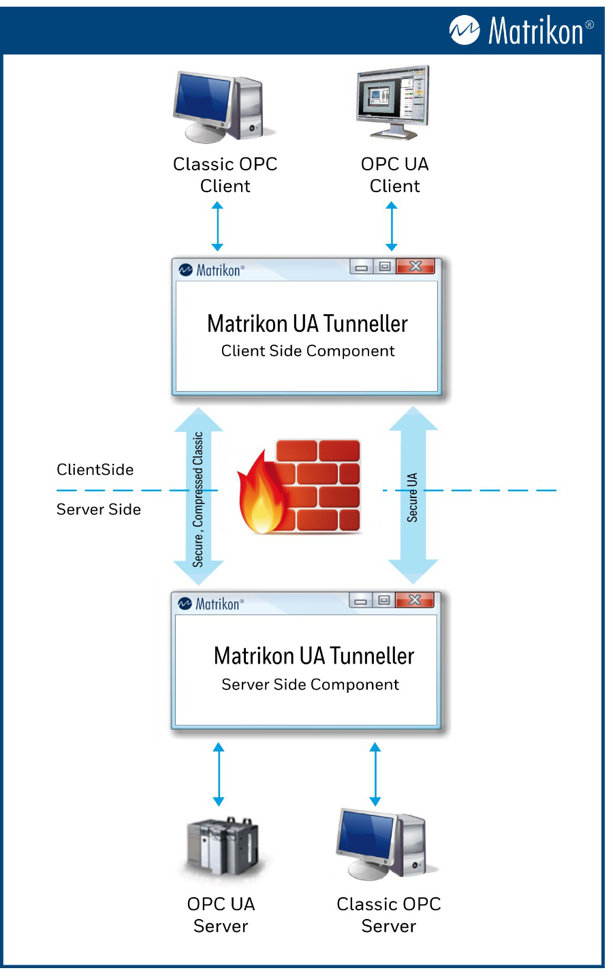
虹科荣誉 | 虹科工业物联网产品荣获中国自动化产业年会用户信赖产品奖!
2023 虹科荣获2021年度中国自动化产业年会用户信赖产品奖 近日,2023中国自动化产业年会于北京隆重举行。虹科工业物联网的产品“OPC UA Tunneller软件”凭借其产品优势和市场美誉度,通过层层选拔,在本次大会中荣获2021年度用户信赖产品奖。…...

SwiftUI 如何让文本自动支持查找和替换功能?
概览 有些情况下,我们需要为文本编辑器实现文本的查找和替换功能(find & replace),如果完全靠自已撸码还是比较棘手的。 所幸的是,从 SwiftUI 4.0 (iOS 16)开始,Apple 已经将查…...
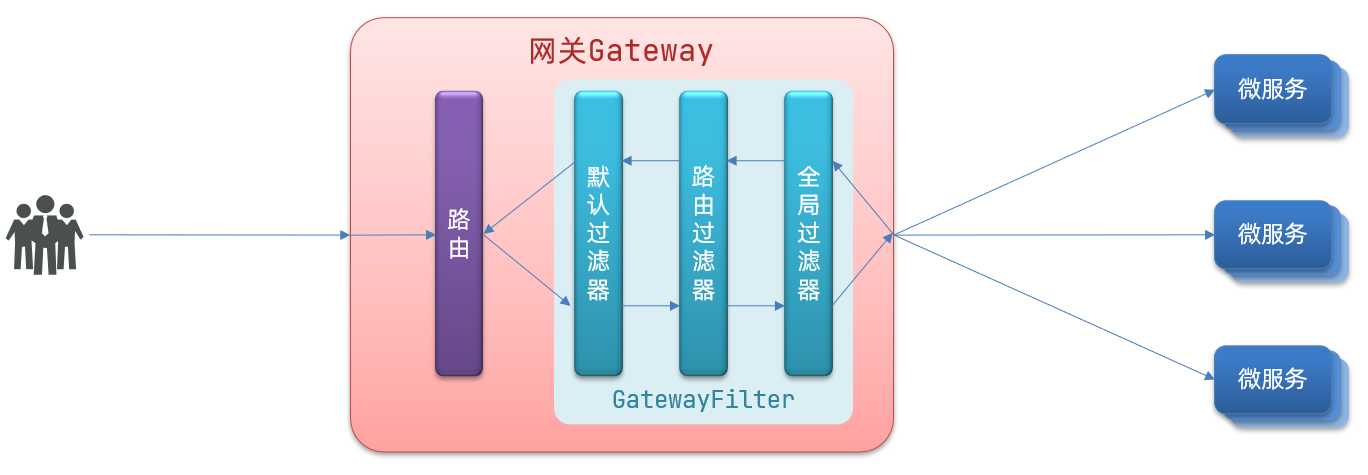
SpringCloud全面学习笔记之初尝美妙篇
目录 前言初识微服务单体架构分布式架构微服务架构初见SpringCloud微服务治理分布式服务架构案例 微服务组件及使用Eureka注册中心提供者和消费者Eureka的结构和作用搭建Eureka服务注册服务服务发现Eureka注册服务总结 Ribbon负载均衡原理负载均衡原理负载均衡策略懒加载 Nacos…...

Spring MVC框架
Spring MVC框架 Spring MVC属于SpringFrameWork的后续产品,已经融合在Spring Web Flow里面。Spring 框架提供了构建 Web 应用程序的全功能 MVC 模块。使用 Spring 可插入的 MVC 架构,从而在使用Spring进行WEB开发时,可以选择使用Spring的Spri…...

Illustrator如何使用图层与蒙版之实例演示?
文章目录 0.引言1.绘制可爱冰淇淋图标2.霓虹渐变立体文字海报3.炫彩花纹背景 0.引言 因科研等多场景需要进行绘图处理,笔者对Illustrator进行了学习,本文通过《Illustrator CC2018基础与实战》及其配套素材结合网上相关资料进行学习笔记总结,…...

Office Tool Plus的使用
是否为安装,卸载,激活Office而烦恼? 下载 地址:Office Tool Plus 官方网站 - 一键部署 Office 安装office 先安装Office,Office_Pro_Plus_2021_LTSCProjectVisio_x64_zh_CN_VL_2022-02 注意,要安装批量…...
射频PCB 设计的六大条技巧
即使是最自信的设计人员,对于射频电路也往往望而却步,因为它会带来巨大的设计挑战,并且需要专业的设计和分析工具。这里将为您介绍六条技巧,来帮助您简化任何射频PCB 设计任务和减轻工作压力! 1、保持完好、精确的射频…...

优化了成本和安装难度后,UWB信标能否取代蓝牙信标?
1 我们做安U3号是要解决什么问题? (1)信标式设计,解决传统UWB基站安装过程繁琐复杂的问题 传统UWB基站在安装过程中遇上的难题: l 安装位置选取问题:UWB基站的准确度与其安装位置有很大关系,…...

深入理解Java虚拟机——垃圾回收算法
1.前言 垃圾回收需要完成的三件事 首先我们需要明白垃圾回收需要完成的三件事: 哪些内存需要回收 堆内存中的对象所使用的内存方法区中的废弃的常量以及不再使用的类型 什么时候回收 当对象死亡方法区中某些内容(常量和类型)不再被使用 如…...

git-rebase和merge
A-----B----C----D master E----F-----G feature 为了把main分支里新增的代码应用在你的feature分支,你有两种方法:merge 和 rebase。 merge git checkout feature git merge main A-----B----C----D master E----F-----G -----* feature (合并master…...

【JavaWeb 用户认证】Cookie、Session、Token、JWT、Interceptor、SpringBoot、Spring Security
Token基本了解:【详细阐述Token的来源】公钥私钥基本了解:【理解公钥】 文章目录 一、Cookie 经典介绍以及使用案例二、Session 经典介绍以及拦截登录案例三、Token MySQL 的基本介绍及其基本使用四、JWT 基本介绍及其基本讲解五、SpringBoot 使用拦截器…...

6个月的测试,来面试居然要15K,我一问连5K都不值
2023年4月份我入职了深圳某家创业公司,刚入职还是很兴奋的,到公司一看我傻了,公司除了我一个自动化测试,公司的测试人员就只有2个开发3个前端1个测试还有2个UI,在粗略了解公司的业务后才发现是一个从零开始的项目&…...

RSA--维纳攻击--代码和题目分析
文章目录 维纳攻击原理:维纳攻击脚本[羊城杯 2020]RRRRRRRSA 1题目描述:题目分析: 收获与体会: 维纳攻击原理: 两位大佬讲得非常清楚(搬运工就是我):https://zhuanlan.zhihu.com/p/…...
飞腾ft2000-麒麟V10-SP1安装Docker、运行gitlab容器
目录 一、安装及配置docker 1、卸载docker相关包及删除相关配置文件 2、安装二进制docker 1.下载软件包 2.解压 3.修改镜像加速地址 4.修改profile文件 5.启动docker 6.docker常用命令 二、安装并启动gitlab镜像 1.安装gitlab镜像 1.查询满足使用需求的gitlab版本 2…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
