Leecode101 ——对称二叉树
对称二叉树:Leecode 101
leecode 101 对称二叉树
根据题目描述,首先想清楚,对称二叉树要比较的是哪两个节点。对于二叉树是否对称,要比较的是根节点的左子树与根节点的右子树是不是相互翻转的,其实也就是比较两个树,即根节点的左右子树,所以在遍历的过程中,也要同时遍历两棵树。(参考:代码随想录)
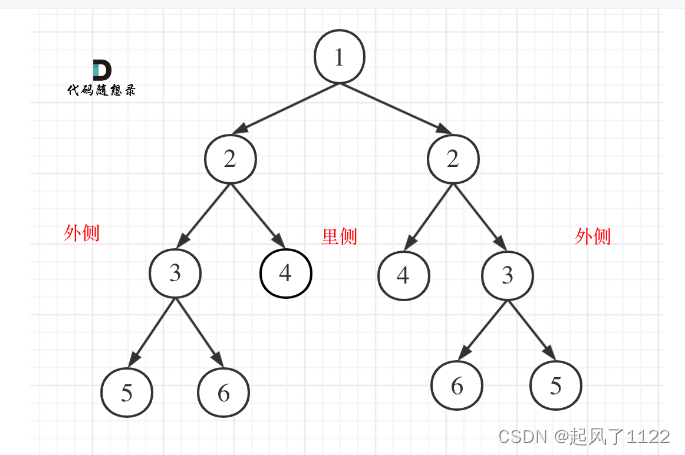
那要怎么比较呢,比较的是两个子树的里侧和外侧元素是否相等。
使用递归法的三部曲:
1.确定递归的参数和返回值
因为要比较的是根节点的左右子树是否相互翻转的,进而判断是否对称二叉树,所以要比较两个树,参数即左子树节点和右子树节点,返回值也就是boolean类型。
2.确定终止条件
根据上面的条件可以总结出,终止条件分为以下几种情况:
节点为空的情况有:(1)判断根节点的左节点是否为空,如果左右节点都为空,那就是对称二叉树,返回true
(2)当其中一个节点为空另一个不为空则不是对称二叉树,return false
此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:(3)若左右节点不为空,那么剩下的就是比较左右的数值情况:
若左右节点不为空,左子树的值不等于右子树的值也不是对称二叉树。return false
3.确定单层递归逻辑
单层递归逻辑就是处理左右节点都不为空且数值相同的情况,
(1)比较二叉树外侧是否相等,即传入左节点的左孩子和右节点的右孩子;
(2)比较内测是否相等,传入左节点的右孩子和右节点的左孩子。
(3)如果都相等返回TRUE
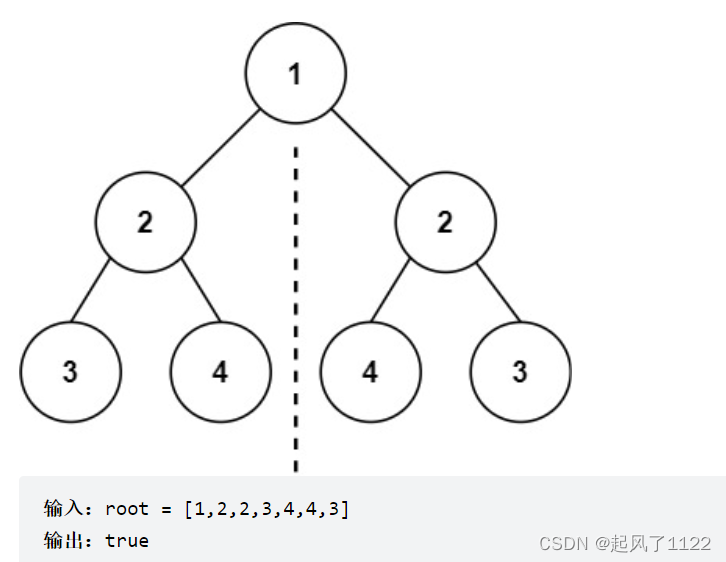
代码如下:
public boolean isSymmetric1(TreeNode root) {return compare(root.left, root.right);}private boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) {return false;}if (left != null && right == null) {return false;}if (left == null && right == null) {return true;}if (left.val != right.val) {return false;}// 比较外侧boolean compareOutside = compare(left.left, right.right);// 比较内侧boolean compareInside = compare(left.right, right.left);return compareOutside && compareInside;}相关文章:

Leecode101 ——对称二叉树
对称二叉树:Leecode 101 leecode 101 对称二叉树 根据题目描述,首先想清楚,对称二叉树要比较的是哪两个节点。对于二叉树是否对称,要比较的是根节点的左子树与根节点的右子树是不是相互翻转的,其实也就是比较两个树,…...
JVM学习随笔03——Java堆中new一个对象的步骤
目录 一、进行类加载 二、堆中分配内存 1、怎么输出GC日志: 2、内存分配的两种方式: 3、内存分配过程中并发控制的两种方式: 三、内存空间初始化 四、对象头初始化(对象头包含哪些信息?) 五、执行构…...
虹科方案 | CEMEX 使用HK-Edgility 智能边缘计算平台简化其企业 WAN 管理和运营
一、应对价值 130 亿美元的跨国企业的网络挑战 “我们选择 Edgility 是因为其卓越的管理和协调功能,它为我们提供了一个端到端的工具集,可以经济高效地部署和管理我们边缘设备的生命周期。” —— Fernando Garcia -Villaraco Casero, CEMEX 全球IT 战略…...

rk3568 系统移植和编译
1。 硬件问题 尽量根据原版 evb 开发版 pcb 进行布线和移植,切记不可自行走线。 emmc 和 ddr4 选型都有要求的,按照硬件手册进行设计 2。软件问题 2.1 目前固件系统选用1.3.2 版本进行设计 解压后运行 .repo/repo/repo sync -c 更新代码 2.2 ubo…...

深度解析C++异常处理机制:分类、处理方式、常见错误及11新增功能
C 基础知识 八 异常处理 上篇 一、基础1. 异常的概念2. 异常的分类2.1 内置异常2.2 自定义异常 3. 异常的处理方式3.1 try-catch 语句3.2 throw 语句3.3 noexcept 修饰符3.4 finally 语句块 二、 异常处理机制1 try-catch 语句块2 异常处理流程3 标准异常类 三、 抛出异常1 thr…...
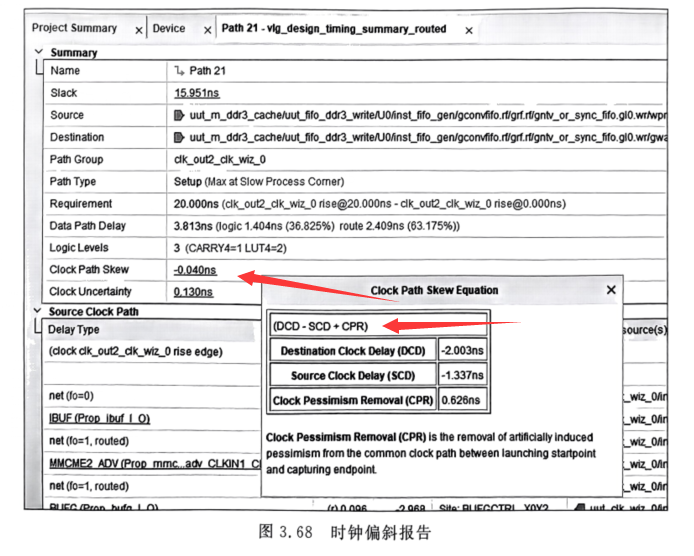
FPGA时序约束(四)主时钟、虚拟时钟和时钟特性的约束
系列文章目录 FPGA时序约束(一)基本概念入门及简单语法 FPGA时序约束(二)利用Quartus18对Altera进行时序约束 FPGA时序约束(三)时序约束基本路径的深入分析 文章目录 系列文章目录前言主时钟约束跨时钟域…...

JNI开发
文件结构(选中的为生成的) CMake构建不需要执行命令,会自动生成so文件打包进apk Android mk构建需要执行命令生成so文件,再打包进apk。命令如下。 # 在jni目录下执行 # 生成com_demo_cppproject_OtherNdkTest.h头文件 javac -h .…...

JAVA有哪些特点?
JAVA有以下特点: 综上所述,Java作为一种先进的面向对象编程语言,具有简单、可移植、健壮、高性能、多线程、动态性、跨平台、开放性和安全性等众多特点,已经成为广泛使用的编程语言之一。 简单易学:JAVA语言的语法与C语…...
使用读写锁提高并发
我们想要的是:允许多个线程同时读,但只要有一个线程在写,其他线程就必须等待。 ReadWriteLock ReadWriteLock的作用: 只允许一个线程写入(其他线程既不能写入也不能读取);没有写入时…...

使用@PropertySource加载配置文件
1.PropertySource和PropertySources注解 1.1.PropertySource注解概述 PropertySource注解是Spring 3.1开始引入的配置类注解。通过**PropertySource注解可以将properties配置文件中的key/value存储到Spring的Environment中,Environment接口提供了方法去读取配置文…...

事务及分布式事务解决方案
基础概念 1.1.事务 事务可以看做是一次大的活动,它由不同的小活动组成,这些活动要么全部成功,要么全部失败。 1.2.本地事务 在计算机系统中,更多的是通过关系型数据库来控制事务,利用数据库本身的事务特性来实现&a…...

【思科、华为、华三、锐捷网络设备巡检命令】
华三 screen-1ength disable 取消分页 displayversion 查看版本 displayclock 查看日期时钟 displayfan 查看风扇状态 displaypower 查看电源信息 displaycpu-usage 查看CPU利用率 displaymemory 查看内存利用率 display environment 查看温度信息 display device 查看设备信息…...

代码随想录算法训练营第五十二天
代码随想录算法训练营第五十二天| 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组 300.最长递增子序列674. 最长连续递增序列718. 最长重复子数组 300.最长递增子序列 题目链接:最长递增子序列 这里是不用处理if nums[i] &l…...

【Linux网络】传输层中UDP和TCP协议
文章目录 1、再谈端口号2、UDP协议3、TCP协议3.1 TCP协议段格式3.2 TCP的三次握手和四次挥手(连接管理机制)3.3 TCP的滑动窗口3.4 TCP的流量控制3.5 拥塞控制3.6 延迟应答和捎带应答3.7 面向字节流和粘包问题3.8 TCP总结 1、再谈端口号 端口号port标识一…...

工具︱ Web3加密浏览器Brave有什么特别之处?
使用浏览器来上网访问和获取各种信息和资源已经成为传统互联网民的普遍活动,下一代互联网协议Web3的核心特点是去中心化,即不依赖于中心化的服务器和数据中心,而是通过分布式的网络节点来实现数据存储和传输。 浏览器承载着信息网络与用户需求…...

绝对不能错过这份沃尔玛实用插件工具大全
龙哥最近发现很多跨境卖家都比较少运营沃尔玛这个平台。沃尔玛除了是世界500强之外,它的线上商城也弄得很好。它的电商平台主要是售卖自营的,然后你也可以入驻来卖自己的产品,就像是我们国内的京东一样。今天龙哥就给大家分享一些沃尔玛专用插…...

【Java】字符串模板拼接的方法
引 在Java中,构建字符串是非常常见的操作。在很多时候,我们都需要使用变量或输入来定制一个文本输出,例如打印日志、生成HTML代码或构建错误消息。而当需要进行字符串连接时,字符串模板是一种常用的方法。在本篇博客中࿰…...

Vue3项目中使用ECharts图表并实现自适应效果
文章目录 一、Vue3项目安装ECharts二、引入、使用ECharts1.创建图表组件,并在父组件中引入使用2.引入ECharts3.ECharts图表自适应 总结 一、Vue3项目安装ECharts 在项目中输入如下代码: npm install echarts --save安装完成可以在package.json中看到&a…...
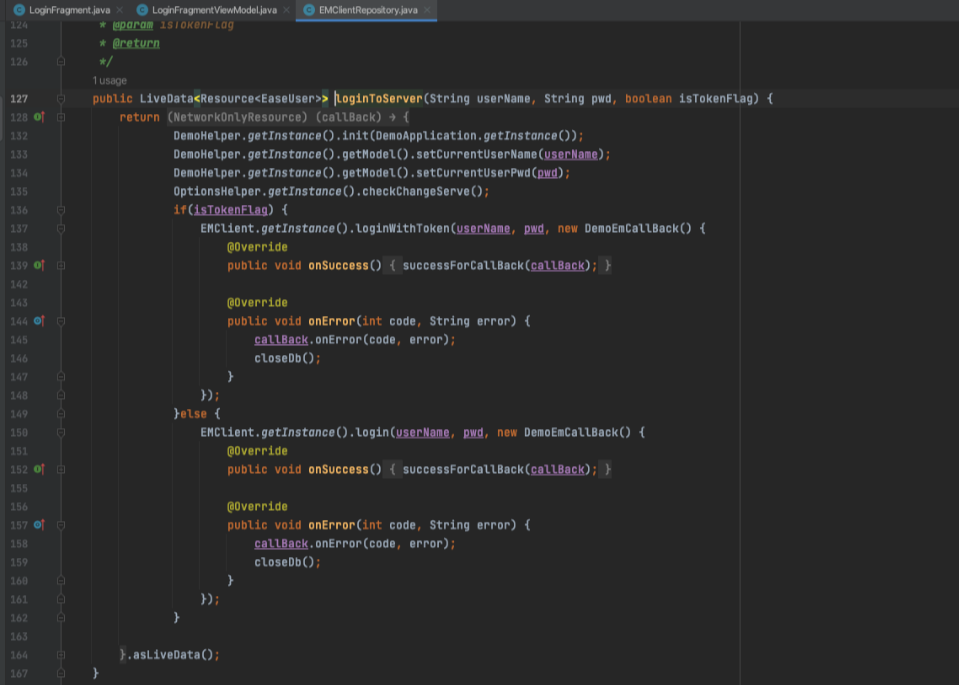
快速跑通环信IM Android Demo
1、以Android 4.0.0 Demo为例 https://www.easemob.com/download/demo (下载别的版本的demo 可以修改版本号直接下载就就可以) https://downloadsdk.easemob.com/downloads/easemob-sdk-4.0.0.zip 运行时遇到以下报错在项目build.gradle中添加运行时遇…...
1190 - 1196 题)
leetcode解题思路分析(一百三十九)1190 - 1196 题
反转每对括号间的子串 给出一个字符串 s(仅含有小写英文字母和括号)。请你按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串,并返回最终的结果。注意,您的结果中 不应 包含任何括号。 可以简单的用栈保存当前层…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
