【高等数学笔记】Stolz定理
文章目录
- Stolz定理
- 例子
- 1. 算术平均数的极限
- 2.
Stolz定理可以被理解为“数列的洛必达法则”,它揭示了两个数列之比的极限和相邻两项之差的比的极限的关系。
Stolz定理
∗ ∞ \cfrac{*}{\infty} ∞∗型
定理1 设 { a n } \{a_n\} {an}和 { b n } \{b_n\} {bn}是两个实数列,其中 { b n } \{b_n\} {bn}是严格单调的且趋向于无穷( + ∞ +\infty +∞或 − ∞ -\infty −∞)。若极限 lim n → ∞ a n + 1 − a n b n + 1 − b n = l \lim\limits_{n\to\infty}\cfrac{a_{n+1}-a_n}{b_{n+1}-b_n}=l n→∞limbn+1−bnan+1−an=l存在,则 lim n → ∞ a n b n = l \lim\limits_{n\to\infty}\cfrac{a_n}{b_n}=l n→∞limbnan=l。
证明: 不妨设 lim n → ∞ b n = + ∞ \lim\limits_{n\to\infty}b_n=+\infty n→∞limbn=+∞,且 { b n } \{b_n\} {bn}严格单调递增。由 lim n → ∞ a n + 1 − a n b n + 1 − b n = l \lim\limits_{n\to\infty}\cfrac{a_{n+1}-a_n}{b_{n+1}-b_n}=l n→∞limbn+1−bnan+1−an=l知, ∀ ε 2 > 0 \forall\cfrac{\varepsilon}{2}>0 ∀2ε>0, ∃ N \exists N ∃N,使得 ∀ n > N \forall n>N ∀n>N,都有 ∣ a n + 1 − a n b n + 1 − b n − l ∣ < ε 2 \left|\cfrac{a_{n+1}-a_n}{b_{n+1}-b_n}-l\right|<\frac{\varepsilon}{2} bn+1−bnan+1−an−l <2ε即 l − ε 2 < a n + 1 − a n b n + 1 − b n < l + ε 2 l-\cfrac{\varepsilon}{2}<\cfrac{a_{n+1}-a_n}{b_{n+1}-b_n}<l+\cfrac{\varepsilon}{2} l−2ε<bn+1−bnan+1−an<l+2ε因为 { b n } \{b_n\} {bn}严格单调递增,所以 b n + 1 − b n > 0 b_{n+1}-b_n>0 bn+1−bn>0。因此 ( l − ε 2 ) ( b n + 1 − b n ) < a n + 1 − a n < ( l + ε 2 ) ( b n + 1 − b n ) \left(l-\cfrac{\varepsilon}{2}\right)(b_{n+1}-b_n)<a_{n+1}-a_n<\left(l+\cfrac{\varepsilon}{2}\right)(b_{n+1}-b_n) (l−2ε)(bn+1−bn)<an+1−an<(l+2ε)(bn+1−bn)注意到 a n = ( a n − a n − 1 ) + ( a n − 1 + a n − 2 ) + ⋯ + ( a N + 2 − a N + 1 ) + a N + 1 a_n=(a_n-a_{n-1})+(a_{n-1}+a_{n-2})+\cdots+(a_{N+2}-a_{N+1})+a_{N+1} an=(an−an−1)+(an−1+an−2)+⋯+(aN+2−aN+1)+aN+1,那么我们就可以给出 a n a_n an的下界: a N > ( l − ε 2 ) ( b n − b n − 1 ) + ( l − ε 2 ) ( b n − 1 − b n − 2 ) + ⋯ + ( l − ε 2 ) ( b N + 2 − b N + 1 ) + a N + 1 = ( l − ε 2 ) ( b n − b N + 1 ) + a N + 1 \begin{aligned} a_N&>\left(l-\cfrac{\varepsilon}{2}\right)(b_{n}-b_{n-1})+\left(l-\cfrac{\varepsilon}{2}\right)(b_{n-1}-b_{n-2})+\cdots+\left(l-\cfrac{\varepsilon}{2}\right)(b_{N+2}-b_{N+1})+a_{N+1}\\ &=\left(l-\cfrac{\varepsilon}{2}\right)(b_{n}-b_{N+1})+a_{N+1} \end{aligned} aN>(l−2ε)(bn−bn−1)+(l−2ε)(bn−1−bn−2)+⋯+(l−2ε)(bN+2−bN+1)+aN+1=(l−2ε)(bn−bN+1)+aN+1同时也可以给出上界: a N < ( l + ε 2 ) ( b n − b N + 1 ) + a N + 1 a_N<\left(l+\cfrac{\varepsilon}{2}\right)(b_{n}-b_{N+1})+a_{N+1} aN<(l+2ε)(bn−bN+1)+aN+1由于 lim n → ∞ b n = + ∞ \lim\limits_{n\to\infty}b_n=+\infty n→∞limbn=+∞,故 ∃ N ′ \exists N' ∃N′,使得 ∀ n > N ′ \forall n>N' ∀n>N′,有 b n > 0 b_n>0 bn>0。(即 b n b_n bn在某项之后恒为正。)现在,对于 n > max { N , N ′ } n>\max\{N,N'\} n>max{N,N′},给 a n a_n an的上下界两边除以 b n b_n bn: ( l − ε 2 ) − ( l − ε 2 ) b N + 1 b n + a N + 1 b n < a n b n < ( l + ε 2 ) − ( l + ε 2 ) b N + 1 b n + a N + 1 b n \left(l-\cfrac{\varepsilon}{2}\right) \textcolor{blue}{-\left(l-\cfrac{\varepsilon}{2}\right)\frac{b_{N+1}}{b_{n}}+\cfrac{a_{N+1}}{b_{n}}} <\cfrac{a_n}{b_n}< \left(l+\cfrac{\varepsilon}{2}\right) \textcolor{green}{-\left(l+\cfrac{\varepsilon}{2}\right)\cfrac{b_{N+1}}{b_{n}}+\cfrac{a_{N+1}}{b_{n}}} (l−2ε)−(l−2ε)bnbN+1+bnaN+1<bnan<(l+2ε)−(l+2ε)bnbN+1+bnaN+1注意 − ( l − ε 2 ) b N + 1 b n + a N + 1 b n \textcolor{blue}{-\left(l-\cfrac{\varepsilon}{2}\right)\frac{b_{N+1}}{b_{n}}+\cfrac{a_{N+1}}{b_{n}}} −(l−2ε)bnbN+1+bnaN+1和 − ( l + ε 2 ) b N + 1 b n + a N + 1 b n \textcolor{green}{-\left(l+\cfrac{\varepsilon}{2}\right)\cfrac{b_{N+1}}{b_{n}}+\cfrac{a_{N+1}}{b_{n}}} −(l+2ε)bnbN+1+bnaN+1实际上是趋于 0 0 0的,即 ∀ ε 2 > 0 \forall\cfrac{\varepsilon}{2}>0 ∀2ε>0,存在 N + > N ′ N_+>N' N+>N′和 N − > N ′ N_->N' N−>N′,使得当 n > N ∗ = max { N + , N − } n>N^*=\max\{N_+,N_-\} n>N∗=max{N+,N−}时,有 ∣ − ( l − ε 2 ) b N + 1 b n + a N + 1 b n ∣ < ε 2 ∣ − ( l + ε 2 ) b N + 1 b n + a N + 1 b n ∣ < ε 2 \left|\textcolor{blue}{-\left(l-\cfrac{\varepsilon}{2}\right)\frac{b_{N+1}}{b_{n}}+\cfrac{a_{N+1}}{b_{n}}}\right|<\cfrac{\varepsilon}{2}\\ \left|\textcolor{green}{-\left(l+\cfrac{\varepsilon}{2}\right)\cfrac{b_{N+1}}{b_{n}}+\cfrac{a_{N+1}}{b_{n}}}\right|<\cfrac{\varepsilon}{2} −(l−2ε)bnbN+1+bnaN+1 <2ε −(l+2ε)bnbN+1+bnaN+1 <2ε故 l − ε = l − ε 2 − ε 2 < a n b n < l + ε 2 + ε 2 = l + ε l-\varepsilon=l-\cfrac{\varepsilon}{2}-\cfrac{\varepsilon}{2} < \cfrac{a_n}{b_n} < l+\cfrac{\varepsilon}{2}+\cfrac{\varepsilon}{2}=l+\varepsilon l−ε=l−2ε−2ε<bnan<l+2ε+2ε=l+ε因此,我们证明了: ∀ ε > 0 \forall\varepsilon>0 ∀ε>0, ∃ N ∗ = max { N + , N − } \exists N^*=\max\{N_+,N_-\} ∃N∗=max{N+,N−},使得 ∀ n > N ∗ \forall n>N^* ∀n>N∗,有 ∣ a n b n − l ∣ < ε \left|\cfrac{a_n}{b_n}-l\right|<\varepsilon bnan−l <ε,即 lim n → ∞ a n b n = l \lim\limits_{n\to\infty}\cfrac{a_n}{b_n}=l n→∞limbnan=l。
0 0 \cfrac{0}{0} 00型
定理2 设 { a n } \{a_n\} {an}和 { b n } \{b_n\} {bn}是两个实数列, lim n → ∞ a n = lim n → ∞ b n = 0 \lim\limits_{n\to\infty}a_n=\lim\limits_{n\to\infty}b_n=0 n→∞liman=n→∞limbn=0且 b n b_n bn严格单调递减。若极限 lim n → ∞ a n + 1 − a n b n + 1 − b n = l \lim\limits_{n\to\infty}\cfrac{a_{n+1}-a_n}{b_{n+1}-b_n}=l n→∞limbn+1−bnan+1−an=l存在,则 lim n → ∞ a n b n = l \lim\limits_{n\to\infty}\cfrac{a_n}{b_n}=l n→∞limbnan=l。
证明提要:将 a n a_n an写成 a n = ( a n − a n + 1 ) + ( a n + 1 − a n + 2 ) + ⋯ + ( a n − ν + 1 − a n + ν ) + a n + ν a_n=(a_{n}-a_{n+1})+(a_{n+1}-a_{n+2})+\cdots+(a_{n-\nu+1}-a_{n+\nu})+a_{n+\nu} an=(an−an+1)+(an+1−an+2)+⋯+(an−ν+1−an+ν)+an+ν,然后给出 a n a_n an的上下界,两边同时除以 b n b_n bn,注意到 a n + ν a_{n+\nu} an+ν和 b n + ν b_{n+\nu} bn+ν趋于 0 0 0即可证明。
例子
1. 算术平均数的极限
我们要证明 lim n → ∞ x 1 + x 2 + ⋯ + x n n = lim n → ∞ x n \lim\limits_{n\to\infty}\cfrac{x_1+x_2+\cdots+x_n}{n}=\lim\limits_{n\to\infty}x_n n→∞limnx1+x2+⋯+xn=n→∞limxn。
定义 a n = x 1 + x 2 + ⋯ + x n a_n=x_1+x_2+\cdots+x_n an=x1+x2+⋯+xn, b n = n b_n=n bn=n。则要证 lim n → ∞ a n b n = lim n → ∞ x n \lim\limits_{n\to\infty}\cfrac{a_n}{b_n}=\lim\limits_{n\to\infty}x_n n→∞limbnan=n→∞limxn。注意到 a n + 1 − a n = x n a_{n+1}-a_{n}=x_n an+1−an=xn, b n + 1 − b n = 1 b_{n+1}-b_{n}=1 bn+1−bn=1,现在该怎么做应该很明显了。
2.
求 lim n → ∞ [ ( n + 1 ) ! n + 1 − n ! n ] \lim\limits_{n\to\infty}\left[\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}\right] n→∞lim[n+1(n+1)!−nn!]。
令 a n = n ! n a_n=\sqrt[n]{n!} an=nn!, b n = n b_n=n bn=n,则 lim n → ∞ [ ( n + 1 ) ! n + 1 − n ! n ] = lim n → ∞ a n + 1 − a n b n + 1 − b n = lim n → ∞ a n b n = lim n → ∞ n ! n n \lim\limits_{n\to\infty}\left[\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}\right]=\lim\limits_{n\to\infty}\cfrac{a_{n+1}-a_{n}}{b_{n+1}-b_{n}}=\lim\limits_{n\to\infty}\cfrac{a_{n}}{b_{n}}=\lim\limits_{n\to\infty}\frac{\sqrt[n]{n!}}{n} n→∞lim[n+1(n+1)!−nn!]=n→∞limbn+1−bnan+1−an=n→∞limbnan=n→∞limnnn!根据Stirling公式, n ! ∼ 2 π n ( n e ) n n!\sim\sqrt{2\pi n}{\left(\cfrac{n}{e}\right)}^n n!∼2πn(en)n,故 lim n → ∞ n ! n n = lim n → ∞ ( 2 π n ) 1 2 n ⋅ n e n = 1 e \lim\limits_{n\to\infty}\frac{\sqrt[n]{n!}}{n}=\lim\limits_{n\to\infty}\cfrac{{(2\pi n)}^{\frac{1}{2n}}\cdot \cfrac{n}{e}}{n}=\cfrac{1}{e} n→∞limnnn!=n→∞limn(2πn)2n1⋅en=e1
相关文章:

【高等数学笔记】Stolz定理
文章目录 Stolz定理 ∗ ∞ \cfrac{*}{\infty} ∞∗型 0 0 \cfrac{0}{0} 00型 例子1. 算术平均数的极限2. Stolz定理可以被理解为“数列的洛必达法则”,它揭示了两个数列之比的极限和相邻两项之差的比的极限的关系。 Stolz定理 ∗ ∞ \cfrac{*}{\infty} ∞∗型…...

【24】核心易中期刊推荐——图像处理研究大数据及智能处理研究
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...
【A、B、C、D】)
Codeforces Round 870 (Div. 2)【A、B、C、D】
文章目录 A. Trust Nobody(暴力)B. Lunatic Never Content(数学)C. Dreaming of Freedom(数学、暴力)D. Running Miles(前缀、后缀) 传送门 A. Trust Nobody(暴力) 题意:给出n个人的陈述,每个人陈述至少有ai个人说谎,让你求出可能是说谎人数…...
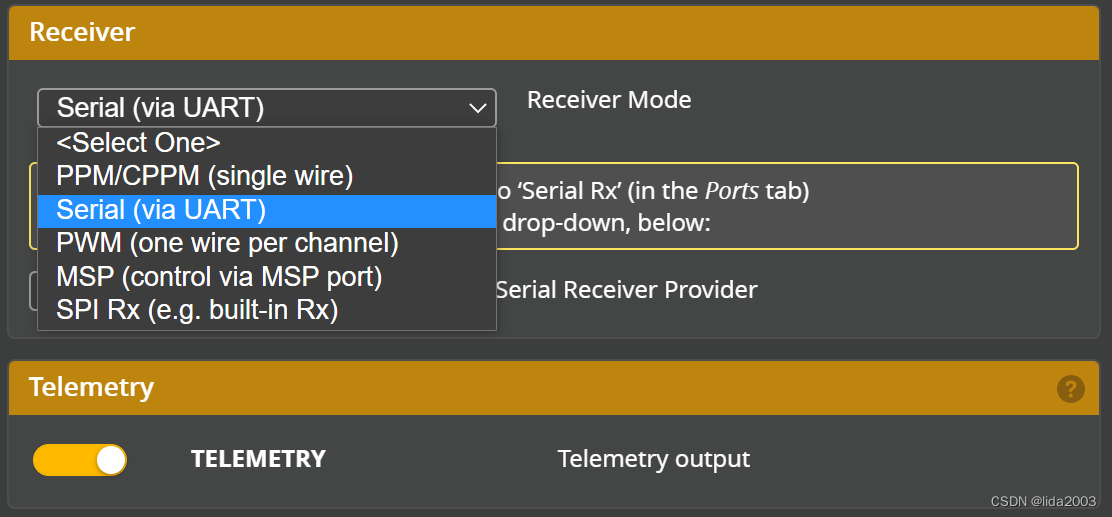
BetaFlight统一硬件AOCODARC H7DUAL配置文件讨论
BetaFlight统一硬件AOCODARC H7DUAL配置文件讨论 1. 源由2. Review配置3. 分析整理3.1 生产商信息3.2 磁力计3.3 气压计3.4 陀螺仪3.5 串口RxTx3.6 板载Flash3.7 模拟OSD MAX74563.8 PPM接收机3.9 伺服器3.10 LED灯带3.11 蜂鸣器3.12 电机 X83.13 ADC(电压/电流/RSSI信号强度/空…...

力扣题库刷题笔记682-棒球比赛
1、题目如下: 2、个人Python代码实现如下: 代码如下: class Solution: def calPoints(self, operations: List[str]) -> int: i 0 #用于遍历元素的下标 while i < len(operations): …...

SpringCloud------Eureka修改实例显示信息、服务发现Discovery、自我保护(六)
SpringCloud------Eureka修改实例显示信息、服务发现Discovery、自我保护(六) 1.actuator微服务信息完善 2.服务发现Discovery 3.Eureka自我保护 actuator微服务信息完善 web和actuator依赖用于图形化监控 1.主机名称:服务名称修改 新增…...

Java 远程debug,IDEA 远程 Debug 调试
有时候我们需要进行远程的debug,本文研究如何进行远程debug,以及使用 IDEA 远程debug的过程中的细节。看完可以解决你的一些疑惑。 配置 远程debug的服务,以SpringBoot微服务为例。 首先,启动SpringBoot需要加上特定的参数。 …...

将webrtc的音频模式改为共享模式
修改音频设备模式:打开文件modules/audio_device/include/audio_device.h,将AudioDeviceModule::kPlatformDefaultAudioProcessing为true改为false。这将禁用默认的音频处理,使得可以修改音频设备模式。 修改音频设备模式的初始化:打开文件modules/audio_device/audio_dev…...
电脑cpu占用率高?怎么办?1分钟快速解决!
案例:电脑cup过高怎么办? 【我的电脑运行缓慢,导致我学习和工作的效率很低。刚刚查看了一下电脑,发现它的cpu占用率很高。有没有小伙伴知道如何解决此电脑cpu过高的问题?】 电脑是我们生活中不可缺少的工具ÿ…...
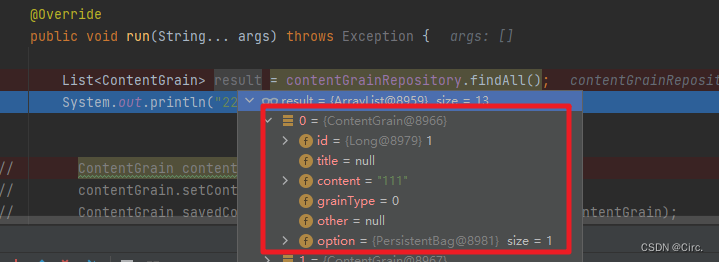
使用JPA自动生成代码(轻松上手看了就会版)
目录 背景:方案概念:JPA 的主要作用 jpa简单使用(Springboot项目)jpa进阶使用总结 背景: 项目需要自动生成sql代码,不需要写sql语句,能够自动进行查询,我想到了JPA。 方案 概念&a…...

jdk动态代理
jdk动态代理:基于反射动态生成代理对象 pwp动态代理的步骤比较复杂,无需特别深入的理解,在jdk中固定的步骤,只需要知道这些步骤即可,不必钻牛角尖 动态代理涉及到的三个反射包类 InvocationHandlerMethodProxy 1. InvocationHand…...

备忘录模式
备忘录模式 备忘录模式定义使用场景1、撤销操作:2、游戏进度保存:3、定时器:4、浏览器历史记录:5、购物车状态保存:6、场景总结 角色定义Originator 发起人角色:Memento 备忘录角色:Caretaker 备忘灵管理员角色:需求背…...

问题解决:跨域访问错误
今天做前端页面渲染的时候遇到一个问题, 因为我使用的wsl开发,windows直接访问不了wsl中的文件,还要改其他配置没成功,索性就不改了,粘贴在桌面上用浏览器打开调试 然后所有使用apifox通过测试的路径全部报错 Ensure CORS response header values are validA cross-origin reso…...

程序员应该怎么自学才能入门 ?我来聊聊自己的经历
当你想成为一名程序员,如何自学入门是一个非常重要的问题。在这里我分享一下我的经验,希望能对你有所帮助。 首先,为了制定好你的学习路线,你可以在网上的培训机构网站找到一张基础路线图。这张路线图必须是跟行业对标的…...

听我一句劝,别去外包,干了6年,废了....
先说一下自己的情况,大专生,18年通过校招进入湖南某软件公司,干了接近6年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了6年的功能测试&…...

leetcode 88 合并两个有序数组
题目描述: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终&am…...
软件项目成本控制的5大关键点 不得不重视
软件项目成本一般分为运营成本和项目成本。而运营成本比较固定,压缩和削减的余地不大。而在项目成本中,最主要的成本是人工成本。那么如何提高项目开发效率,节约人工成本,对成本管理至关重要。 我们从以下几个影响项目成本的主要因…...

CSS样式更改:边框Border的另类用法
CSS样式更改——字体设置Font&边框Border 随着互联网技术的不断发展,网页设计已经成为了一项非常重要的工作。在网页设计中,字体设置和边框Border是两个非常常见的CSS样式,可以通过这两个样式对网页的外观进行设置。下面,我们…...
)
shell的灵活运用 (函数,关联数组,循环,awk,sed等)
题目 提示:没有基础请先看看基础部分的讲解,否则看不懂 1,编写函数,实现判断是否无位置参数,如无参数,提示错误 代码: #bash/bin function a() {b$# #判断传入的参数个数 # echo $b…...
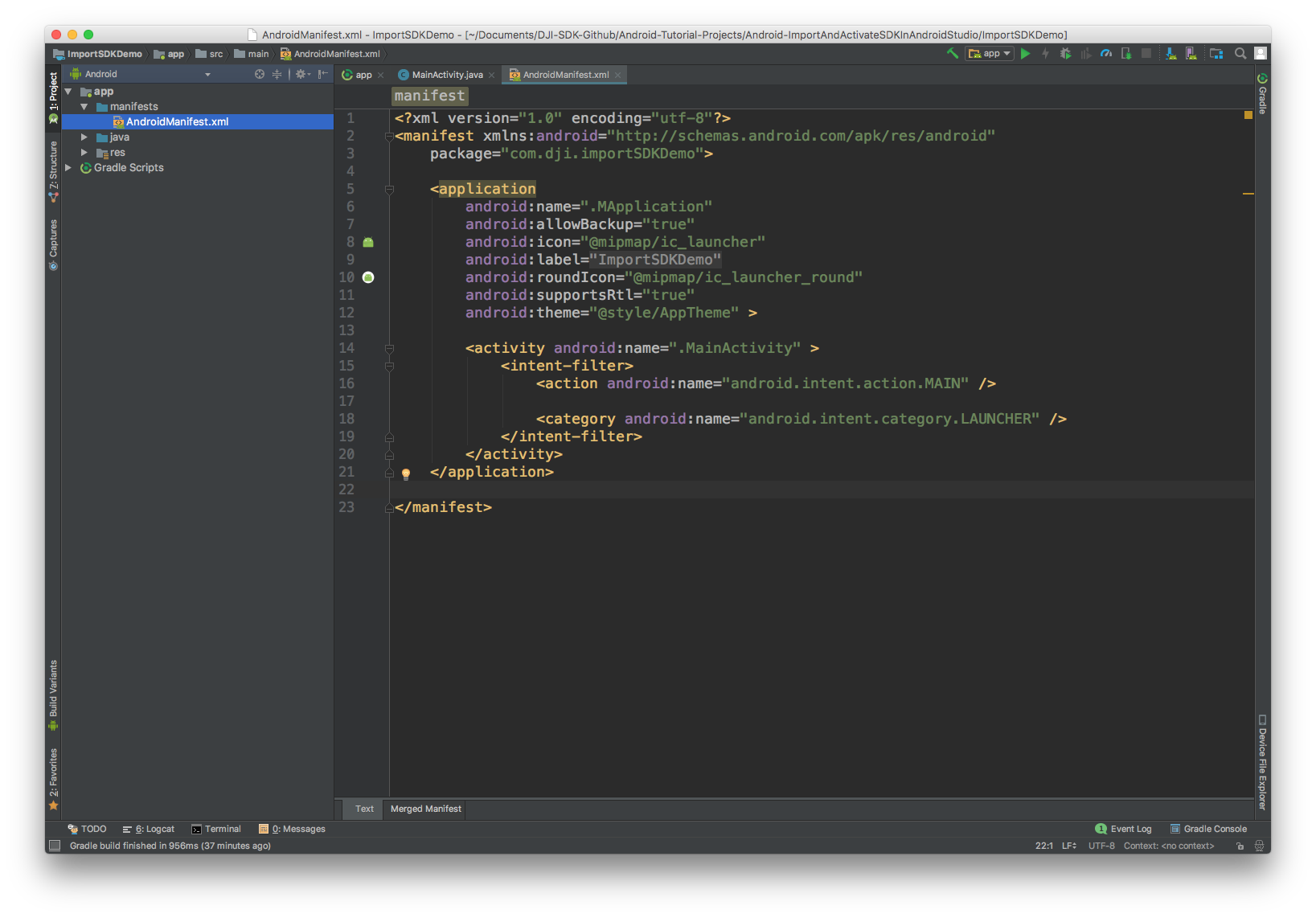
大疆无人机 MobileSDK(遥控器/手机端)开发 v4版<1>
大疆无人机飞控开发 大疆无人机SDK开发包功能概述飞行控制相机实时视频流传感器数据下载媒体文件遥控器,电池和无线链路连接应用程序和产品 v4版sdk 二次开发注册成为DJI开发者生成 App KeyAndroid 示例代码配置Android Studio项目集成创建一个新的应用配置Gradle 脚…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
