均摊时间复杂度
均摊时间复杂度,它对应的分析方法,摊还分析(或者叫平摊分析)
均摊时间复杂度应用的场景比它更加特殊、更加有限
// array表示一个长度为n的数组// 代码中的array.length就等于nint[] array = new int[n];int count = 0;void insert(int val) {if (count == array.length) {int sum = 0;for (int i = 0; i < array.length; ++i) {sum = sum + array[i];}array[0] = sum;count = 1;}array[count] = val;++count;}这段代码实现了一个往数组中插入数据的功能。当数组满了之后,也就是代码中的 count == array.length 时,我们用 for 循环遍历数组求和,并清空数组,将求和之后的 sum 值放到数组的第一个位置,然后再将新的数据插入。但如果数组一开始就有空闲空间,则直接将数据插入数组。
先分析上述代码的时间复杂度
最理想的情况下,数组中有空闲空间,我们只需要将数据插入到数组下标为 count 的位置就可以了,所以最好情况时间复杂度为 O(1)。最坏的情况下,数组中没有空闲空间了,我们需要先做一次数组的遍历求和,然后再将数据插入,所以最坏情况时间复杂度为 O(n)。
平均时间复杂度是多少呢?答案是 O(1)
假设数组的长度是 n,根据数据插入的位置的不同,我们可以分为 n 种情况,每种情况的时间复杂度是 O(1)。除此之外,还有一种“额外”的情况,就是在数组没有空闲空间时插入一个数据,这个时候的时间复杂度是 O(n)。而且,这 n+1 种情况发生的概率一样,都是 1/(n+1)。所以,根据加权平均的计算方法,我们求得的平均时间复杂度就是:
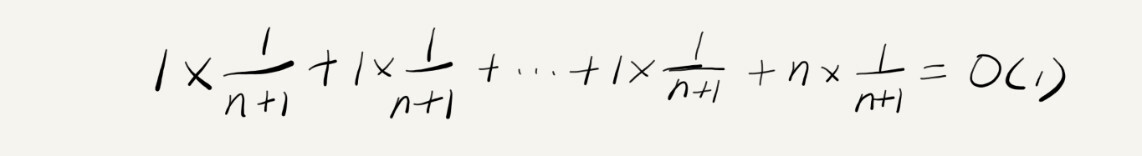
上述的分析过于复杂
可以使用摊还分析法,通过摊还分析得到的时间复杂度我们起了一个名字,叫均摊时间复杂度。
每一次 O(n) 的插入操作,都会跟着 n-1 次 O(1) 的插入操作,所以把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上,均摊下来,这一组连续的操作的均摊时间复杂度就是 O(1)。这就是均摊分析的大致思路。
听起来很复杂,但是均摊时间复杂度就是一种特殊的平均时间复杂度,我们没必要花太多精力去区分它们。你最应该掌握的是它的分析方法,摊还分析。至于分析出来的结果是叫平均还是叫均摊,这只是个说法,并不重要。
此文章为5月Day6学习笔记,内容来源于极客时间《数据结构与算法之美》
相关文章:
均摊时间复杂度
均摊时间复杂度,它对应的分析方法,摊还分析(或者叫平摊分析) 均摊时间复杂度应用的场景比它更加特殊、更加有限 // array表示一个长度为n的数组// 代码中的array.length就等于nint[] array new int[n];int count 0;void insert…...

夏驰和徐策的解决数学问题思路——反证法
反证法是一种证明方法,它的基本思路是通过假设某个结论不成立,然后构造出一个矛盾的情况来推导出原先假设的结论是成立的。 具体来说,反证法一般包含以下步骤: 1. 假设所要证明的命题不成立。 2. 通过这个假设,构造…...

面向开发人员的 ChatGPT 提示词教程 - ChatGPT Prompt Engineering for Developers
面向开发人员的 ChatGPT 提示词教程 - ChatGPT Prompt Engineering for Developers 1. 指南(原文: Guidelines)1-1. 提示的指南(原文: Guidelines for Prompting)1-2. 配置1-3. 提示语原则(原文: Prompting Principles)原则 1: 写出清晰而具体的指示(原文: Write clear and spe…...
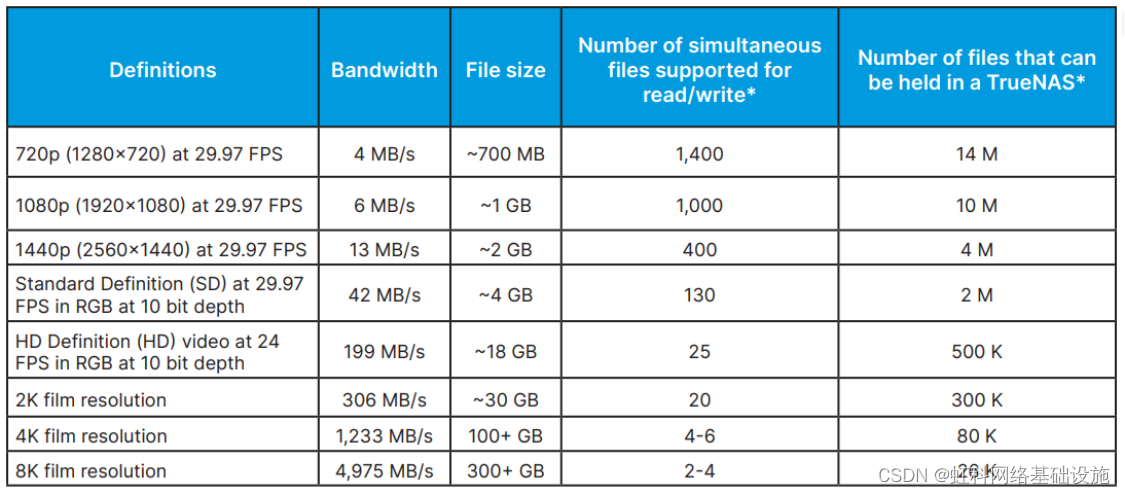
虹科方案|使用 HK-TRUENAS支持媒体和娱乐工作流程-1
一、摘要 开发和交付能够随时随地触及受众的媒体内容变得越来越重要和复杂。 在当今高度互联、娱乐驱动的世界中,媒体和娱乐 (M&E) 公司需要保持竞争力才能取得成功。 这些组织需要制作各种不同格式的信息和娱乐内容,以便在移动设备、台式机、工作站…...

DDR5内存彻底白菜价,国外大厂却整出了比着火更离谱的骚操作
今年的 PC 硬件市场,似乎出现了明显两极分化现象。 一边是 N、A 两家新显卡价格高高在上,摆明了不坑穷人。 另一边固态硬盘、内存条又在疯狂互卷不断杀价。 四五百元的 2TB SSD,二百元的 16G 内存条早已见怪不怪。 要说面世多年的 PCIe 3.0…...
Linux网络——Shell编程之函数
Linux网络——Shell编程之函数 一、概述二、定义函数的格式1.格式一2.格式二 三、函数的查看和删除1.查看 declare2.删除 declare 四、函数的返回值1.return 返回值2.echo 返回值 五、函数的参数传入与变量范围1.函数的传参2.函数变量的作用范围 六、函数的应用1.阶乘2.递归目录…...

GQCNN+PointNetGPD思路和问题--chatGPT
有很多算法是通过神经网络来预测机械臂抓手的抓取位置,其中一些算法需要点云数据作为输入,例如: PointNetGPD:PointNetGPD是一个端到端的基于点云的抓取姿态检测算法。它使用了一个PointNet架构来处理点云输入,并输出每…...

Mysql索引(2):索引结构
1 概述 MySQL的索引是在存储引擎层实现的,不同的存储引擎有不同的索引结构,主要包含以下几种: 索引结构描述BTree索最常见的索引类型,大部分引擎都支持 B 树索引 Hash索引 底层数据结构是用哈希表实现的, 只有精确匹配索引列的…...

Spring框架介绍和应用实践
Spring是一个开源的Java企业应用开发框架,它通过依赖注入和面向切面编程等技术实现了轻量级、松散耦合、可测试和可扩展的应用开发。本文将介绍Spring框架的基本原理和核心功能,以及在实际项目中如何使用Spring框架进行应用开发。 Spring框架基本原理 …...

IO 流学习总结
一:IO 流的概述 1. 什么是 IO 流? 存储和读取数据的解决方法 I:input O:output 流:像水流一样传输数据 2. IO 流的作用? 用于读写数据(本地文件,网络) 3. IO 流按…...

PowerToys——免费、强大、高效的微软官方效率提升工具集,办公学习宝藏软件
名人说:博观而约取,厚积而薄发。——宋苏轼 Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、简单介绍1、PowToys是什么?2、它的功能有哪些?二、下载安装三、功能示例1、始终置顶2、唤醒3、颜色选取器(取色)4、FancyZones(窗口布局)5、File Locksmith6、…...
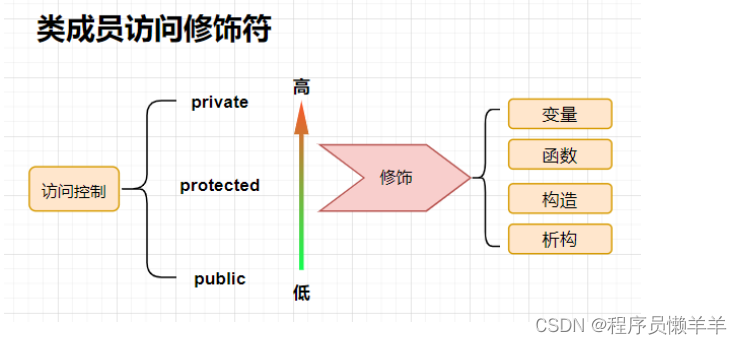
【C++】 类基础汇总(类封装,构造、析构函数...)
目录 前言 正文 类封装 为什么要进行类封装 概念 访问修饰符 构造函数 概念 特点 析构函数 概念 特点 再谈面向过程与面向对象 面向过程 代码举例 面向对象 代码举例 结语 下期预告 前言 在学习过【C语言进阶C】 C基础--让你丝滑的从C语言进阶到C 之后&am…...

BM61-矩阵最长递增路径
题目 给定一个 n 行 m 列矩阵 matrix ,矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的。并输出这条最长路径的长度。 这个路径必须满足以下条件: 对于每个单元格,你可以往上ÿ…...
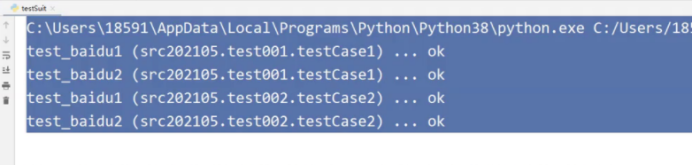
selenium——unittest框架
目录 一、unittest框架基本介绍二、unittest框架解析三、unittest框架使用方法1.测试固件2.测试套件3.用例的执行顺序4.忽略测试用例中的方法5.unittest断言6.HTML报告生成 一、unittest框架基本介绍 在进行selenium IDE脚本录制导出的脚本中,我们发现其中多了很多…...

matlab频谱分析详解
频谱分析是一种用于分析信号频率特征的方法,常用于信号处理、音乐分析、谐波产生等领域。MATLAB是一种功能强大的数字信号处理软件,提供了许多用于频谱分析的函数和工具箱。 本文将介绍如何使用MATLAB进行频谱分析,包括信号预处理、选择合适…...

用layui写用户登录页面遇到的问题
用layui写用户登录页面遇到的问题 1.在layui-row下面的layui-col-md还是换行 原因:link标签和script标签中的type属性没写,导致应该是script或者这个css没有识别出来 解决办法:link标签里面加上type为text/css, script标签中加上type为 2…...
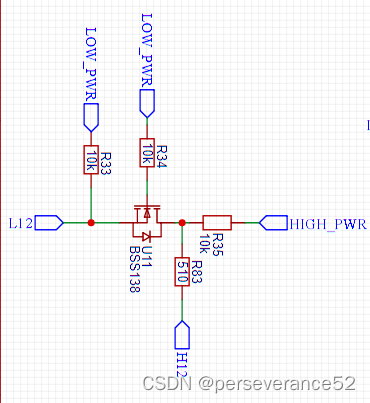
NMOS双向转换电路实测以及上升沿尖峰处理
NMOS双向转换电路实测以及上升沿尖峰处理 NMOS双向转换电路 🔧采用的是5V供电的STC8H单片机输出PWM波形,经过上面的电平转换电路测量低压端的波形。 ✨在做3.3V <>5V 电平转换电路方案验证时,输入5V PWM波形和输出波形的波形上升沿有尖…...
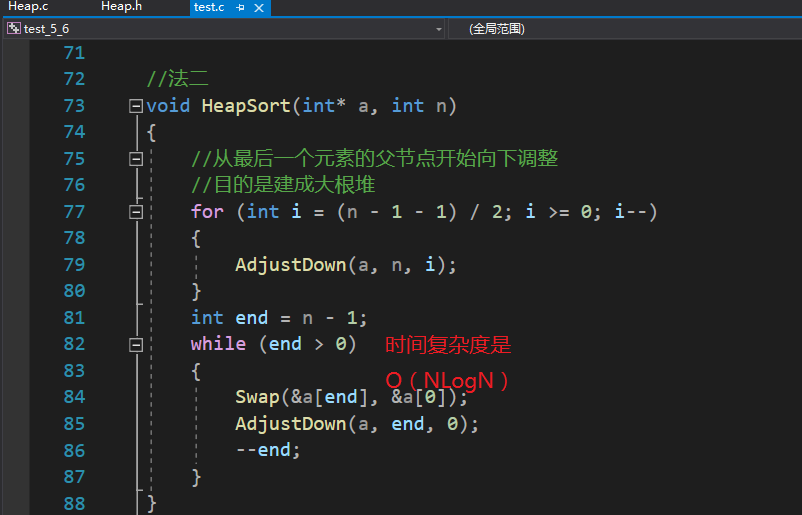
【数据结构】选择排序(详细)
选择排序 1. 直接选择排序2. 堆排序2.1 堆2.2 堆的实现(以大根堆为例)2.3 堆排序 3. 堆排序(topK问题) 1. 直接选择排序 思想 以排升序为例。以a[i]为最大值(或最小值),从a[i1]到a[n-1-i]比较选…...

什么是企业内容管理?
为什么出现企业内容管理? 在数字经济的宏观背景下,企业建立了各种应用系统以满足企业各业务的管理需求,这些系统每天都在产生大量的数据和信息资源,但在企业实践中存在很多数据或资源无法被应用系统获取、处理和共享。 比如发票…...

机器学习:分类、回归、决策树
分类:具有明确的类别 如:去银行借钱,会有借或者不借的两种类别 回归:不具有明确的类别和数值 如:去银行借钱,预测银行会借给我多少钱,如:1~100000之间的一个数值 不纯度࿱…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
