2023河南省赛vp题解
目录
A题:
B题
C题
D题
E题
F题
G题
H题
I题
J题
K题
L题
A题:
1.思路:考虑暴力枚举和双hash,可以在O(n)做完。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
const ull bas = 133331;
const ll mod1 = 1000000033;
const ll mod2 = 1000000103;
typedef pair<int,int> hashv;
hashv pw[N],s1[N],s2[N];
hashv operator + (hashv a,hashv b)
{int c1 = a.fi + b.fi,c2 = a.se + b.se;if(c1 >= mod1) c1 -= mod1;if(c2 >= mod2) c2 -= mod2;return mp(c1,c2);
}
hashv operator - (hashv a,hashv b)
{int c1 = a.fi - b.fi,c2 = a.se - b.se;if(c1 < 0) c1 += mod1;if(c2 < 0) c2 += mod2;return mp(c1,c2);
}
hashv operator * (hashv a,hashv b)
{int c1 = (ll)a.fi * b.fi % mod1,c2 = (ll) a.se * b.se % mod2;return mp(c1,c2);
}
void init(string s)
{int n = sz(s);string t = s;reverse(all(t));t = " " + t;s = " " + s;hashv base = mp(10331,100313);pw[0] = mp(1,1);rep(i,1,n) {pw[i] = pw[i - 1] * base;s1[i] = s1[i - 1] * base + mp(s[i],s[i]);s2[i] = s2[i - 1] * base + mp(t[i],t[i]);
// pw[i] = pw[i - 1] * bas;}
}
hashv get1(int l,int r)
{return s1[r] - s1[l - 1] * pw[r - l + 1];
}
hashv get2(int l,int r)
{return s2[r] - s2[l - 1] * pw[r - l + 1];
}
void solve(){string s;cin >> s;init(s);int n = sz(s);s = " " + s;vector<int> vis(26);rep(i,1,n - 1) {if(vis[s[i] - 'a']) break;vis[s[i] - 'a'] = true; int len = n - i;if(get1(i + 1,n) == get2(1,len)) {cout << "HE" << endl;return;}}cout << "NaN" << endl;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();
}B题
1.思路:暴力枚举+ST表,暴力枚举是调和级数的复杂度。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
#include <functional>
#include <numeric>namespace OY {template <typename _Tp, typename _Maximum>class STTable {std::vector<std::vector<_Tp>> m_sub;_Maximum m_maxi;int m_length;_Tp m_defaultValue;void _check() {// assert(m_maxi(m_defaultValue, m_defaultValue) == m_defaultValue);}public:STTable(int __n = 0, _Maximum __maxi = std::max<_Tp>, _Tp __defaultValue = _Tp()) : m_maxi(__maxi), m_defaultValue(__defaultValue) {_check();resize(__n);}template <typename _Iterator>STTable(_Iterator __first, _Iterator __last, _Maximum __maxi = std::max<_Tp>, _Tp __defaultValue = _Tp()) : m_maxi(__maxi), m_defaultValue(__defaultValue) {_check();reset(__first, __last);}void resize(int __n) {if (!__n) return;m_length = __n;int d = 32 - (m_length > 1 ? __builtin_clz(m_length - 1) : 32);m_sub.resize(d);m_sub[0].assign(__n, m_defaultValue);for (int i = 1; i < d; i++) {m_sub[i].clear();m_sub[i].reserve(m_length - (1 << i) + 1);for (int j = 0; j <= m_length - (1 << i); j++)m_sub[i].push_back(m_maxi(m_sub[i - 1][j], m_sub[i - 1][j + (1 << i - 1)]));}}template <typename _Iterator>void reset(_Iterator __first, _Iterator __last) {m_length = __last - __first;int d = 32 - (m_length > 1 ? __builtin_clz(m_length - 1) : 32);m_sub.resize(d);m_sub[0].assign(__first, __last);for (int i = 1; i < d; i++) {m_sub[i].clear();m_sub[i].reserve(m_length - (1 << i) + 1);for (int j = 0; j <= m_length - (1 << i); j++)m_sub[i].push_back(m_maxi(m_sub[i - 1][j], m_sub[i - 1][j + (1 << i - 1)]));}}void update(int __i, _Tp __val) {m_sub[0][__i] = __val;for (int i = 1; i < m_sub.size(); i++)for (int j = std::max(0, __i - (1 << i) + 1), end = std::min(__i, int(m_sub[i].size() - 1)); j <= end; j++)m_sub[i][j] = m_maxi(m_sub[i - 1][j], m_sub[i - 1][j + (1 << i - 1)]);}_Tp query(int __i) const {return m_sub[0][__i];}_Tp query(int __left, int __right) const {if (__left == __right) return m_sub[0][__left];int d = 31 - __builtin_clz(__right - __left);return m_maxi(m_sub[d][__left], m_sub[d][__right - (1 << d) + 1]);}_Tp queryAll() const {return query(0, m_length - 1);}};template <typename _Tp = int>STTable(int = 0, const _Tp &(*)(const _Tp &, const _Tp &) = std::max<_Tp>, _Tp = _Tp()) -> STTable<_Tp, const _Tp &(*)(const _Tp &, const _Tp &)>;template <typename _Tp = int>STTable(int, _Tp (*)(_Tp, _Tp), _Tp = _Tp()) -> STTable<_Tp, _Tp (*)(_Tp, _Tp)>;template <typename _Maximum, typename _Tp = std::decay_t<typename decltype(std::mem_fn(&_Maximum::operator()))::result_type>>STTable(int, _Maximum, _Tp = _Tp()) -> STTable<_Tp, _Maximum>;template <typename _Iterator, typename _Maximum, typename _Tp = typename std::iterator_traits<_Iterator>::value_type>STTable(_Iterator, _Iterator, _Maximum, _Tp = _Tp()) -> STTable<_Tp, _Maximum>;template <typename _Iterator, typename _Tp = typename std::iterator_traits<_Iterator>::value_type>STTable(_Iterator, _Iterator, const _Tp &(*)(const _Tp &, const _Tp &) = std::max<_Tp>, _Tp = _Tp()) -> STTable<_Tp, const _Tp &(*)(const _Tp &, const _Tp &)>;template <typename _Iterator, typename _Tp = typename std::iterator_traits<_Iterator>::value_type>STTable(_Iterator, _Iterator, _Tp (*)(_Tp, _Tp), _Tp = _Tp()) -> STTable<_Tp, _Tp (*)(_Tp, _Tp)>;
}
int n;
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
int a[N];
void solve(){read(n);rep(i,0,n-1) read(a[i]);auto mymax = [](int x, int y) {return x > y ? x : y;};OY::STTable st_max(a , a + n, mymax);OY::STTable st_min(a , a + n, std::min);int ans = 1;for(int i = 1;i < n;i ++) {bool ok = true;for(int j = i;j <= n;j += i) {if(j == n) break;int nxt = min(j + i,n);int v1 = st_max.query(j - i,j - 1);int v2 = st_min.query(j,nxt - 1);if(v1 > v2) {ok = false;break;}}if(ok) ans ++;}cout << ans << endl;
}
int main()
{ios::sync_with_stdio(false);cout.tie(0);int T = 1;
// cin >> T;while(T --) solve();
}C题
1.思路:考虑验证这个序列,如果出现两个相同的连续超过40的串,那么就认为这个串不随机就行了,错误率就是,实现就是直接kmp搞一下next数组找个最大的看是否大于等于40即可。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define endl '\n'
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
const ll mod = 1e9 + 7;
int a[N],nxt[N];
void get_next(string s)
{int i = 0,j = -1;nxt[0] = -1;int n = s.size();while(i < n) {if(j == -1 || s[i] == s[j]) {i++, j++;nxt[i] = j;}else j = nxt[j];}
}
void solve(){string s,t;s = "";while(cin >> t) s += t; get_next(s);int n = sz(s);int mx = 0;for(int i = 1;i <= n;i ++) mx = max(mx,nxt[i]);if(mx >= 40) cout << "NO" << endl;else cout << "YES" << endl;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;
// cin >> T;while(T --) solve();
}D题 不会
E题
1.思路:考虑dp[i][j][k]表示第i行第j列修改了k个问号的最大值是多少,因为数组内存开不了这么大,因此我们考虑优化空间,我们发现这一行的状态只跟这一行和上一行有关,因此可以滚动dp优化空间。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 501;
int n;
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
int a[N];
string s[N];
void solve(){int m,x;cin >> n >> m >> x;rep(i,1,n) {cin >> s[i];s[i] = " " + s[i];}vector<vector<int>> odp(m + 1,vector<int>(x + 1));odp[1][0] = (s[1][1] == '1');if(s[1][1] == '?' && x >= 1) odp[1][1] = 1;rep(j,1,m) {rep(k,0,x) {int v = s[1][j] == '1';odp[j][k] = max(odp[j - 1][k] + v,odp[j][k]);if(s[1][j] == '?' && k + 1 <= x) odp[j][k + 1] = max(odp[j - 1][k] + 1,odp[j][k + 1]);}}rep(i,2,n) {vector<vector<int>> ndp(m + 1,vector<int>(x + 1));rep(j,1,m) {vector<int> dp(x + 1,0);rep(k,0,x) {int v = s[i][j] == '1';dp[k] = max(ndp[j - 1][k] + v,dp[k]);if(s[i][j] == '?' && k + 1 <= x) dp[k + 1] = max(dp[k + 1],ndp[j - 1][k] + 1);ndp[j][k] = max(ndp[j][k],odp[j][k] + v);if(s[i][j] == '?' && k + 1 <= x) ndp[j][k + 1] = max(ndp[j][k + 1],odp[j][k] + 1);}rep(k,0,x) ndp[j][k] = max(ndp[j][k],dp[k]);}swap(ndp,odp);}int ans = 0;rep(i,0,x) ans = max(ans,odp[m][i]);cout << ans << '\n';
}
int main()
{ios::sync_with_stdio(false);cout.tie(0),cin.tie(0);int T = 1;cin >> T;while(T --) solve();
}F题
1.思路:因为是任意i,j相差取min和max,因此考虑直接排序选k个中最大和最小的一直取min就是答案,考虑用multiset维护即可。
2.代码实现
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int n;
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
int a[N];
void solve(){int n,k;cin >> n >> k;rep(i,1,n) cin >> a[i];sort(a + 1,a + 1 + n);multiset<int> mt;ll ans = 2e18;rep(i,1,n) {if(i > 1) mt.insert(a[i] - a[i - 1]);if(i > k) mt.erase(mt.find(a[i - k + 1] - a[i - k]));if(i >= k) {int mx = a[i] - a[i - k + 1];int mi = *mt.begin();
// cout << i << ',' << mi << ',' << mx << endl;ans = min(ans,1ll * mi * mx);}}cout << ans << endl;
}
int main()
{ios::sync_with_stdio(false);cout.tie(0),cin.tie(0);int T = 1;
// cin >> T;while(T --) solve();
}G题
1.思路:模拟题,考虑特判1的情况就可以了。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int n;
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
int a[N];
string ans[14];
string num[15][100];
string unum[12][100];
void init2()
{unum[0][1] = ".....";unum[0][2] = "00000";unum[0][3] = "0...0";unum[0][4] = "0...0";unum[0][5] = "0...0";unum[0][6] = "00000";unum[0][7] = ".....";unum[0][8] = ".....";unum[0][9] = ".....";unum[0][10] = ".....";unum[1][1] = ".....";unum[1][2] = "....1";unum[1][3] = "....1";unum[1][4] = "....1";unum[1][5] = "....1";unum[1][6] = "....1";unum[1][7] = ".....";unum[1][8] = ".....";unum[1][9] = ".....";unum[1][10] = ".....";unum[2][1] = ".....";unum[2][2] = "22222";unum[2][3] = "....2";unum[2][4] = "22222";unum[2][5] = "2....";unum[2][6] = "22222";unum[2][7] = ".....";unum[2][8] = ".....";unum[2][9] = ".....";unum[2][10] = ".....";unum[3][1] = ".....";unum[3][2] = "33333";unum[3][3] = "....3";unum[3][4] = "33333";unum[3][5] = "....3";unum[3][6] = "33333";unum[3][7] = ".....";unum[3][8] = ".....";unum[3][9] = ".....";unum[3][10] = ".....";unum[4][1] = ".....";unum[4][2] = "4...4";unum[4][3] = "4...4";unum[4][4] = "44444";unum[4][5] = "....4";unum[4][6] = "....4";unum[4][7] = ".....";unum[4][8] = ".....";unum[4][9] = ".....";unum[4][10] = ".....";unum[5][1] = ".....";unum[5][2] = "55555";unum[5][3] = "5....";unum[5][4] = "55555";unum[5][5] = "....5";unum[5][6] = "55555";unum[5][7] = ".....";unum[5][8] = ".....";unum[5][9] = ".....";unum[5][10] = ".....";unum[6][1] = ".....";unum[6][2] = "66666";unum[6][3] = "6....";unum[6][4] = "66666";unum[6][5] = "6...6";unum[6][6] = "66666";unum[6][7] = ".....";unum[6][8] = ".....";unum[6][9] = ".....";unum[6][10] = ".....";unum[7][1] = ".....";unum[7][2] = "77777";unum[7][3] = "....7";unum[7][4] = "....7";unum[7][5] = "....7";unum[7][6] = "....7";unum[7][7] = ".....";unum[7][8] = ".....";unum[7][9] = ".....";unum[7][10] = ".....";unum[8][1] = ".....";unum[8][2] = "88888";unum[8][3] = "8...8";unum[8][4] = "88888";unum[8][5] = "8...8";unum[8][6] = "88888";unum[8][7] = ".....";unum[8][8] = ".....";unum[8][9] = ".....";unum[8][10] = ".....";unum[9][1] = ".....";unum[9][2] = "99999";unum[9][3] = "9...9";unum[9][4] = "99999";unum[9][5] = "....9";unum[9][6] = "99999";unum[9][7] = ".....";unum[9][8] = ".....";unum[9][9] = ".....";unum[9][10] = ".....";
}
//处理下面的数字
void init()
{num[0][1] = ".......";num[0][2] = ".......";num[0][3] = "0000000";num[0][4] = "0.....0";num[0][5] = "0.....0";num[0][6] = "0.....0";num[0][7] = "0.....0";num[0][8] = "0.....0";num[0][9] = "0000000";num[0][10] = ".......";num[1][1] = ".......";num[1][2] = ".......";num[1][3] = "......1";num[1][4] = "......1";num[1][5] = "......1";num[1][6] = "......1";num[1][7] = "......1";num[1][8] = "......1";num[1][9] = "......1";num[1][10] = ".......";num[2][1] = ".......";num[2][2] = ".......";num[2][3] = "2222222";num[2][4] = "......2";num[2][5] = "......2";num[2][6] = "2222222";num[2][7] = "2......";num[2][8] = "2......";num[2][9] = "2222222";num[2][10] = ".......";num[3][1] = ".......";num[3][2] = ".......";num[3][3] = "3333333";num[3][4] = "......3";num[3][5] = "......3";num[3][6] = "3333333";num[3][7] = "......3";num[3][8] = "......3";num[3][9] = "3333333";num[3][10] = ".......";num[4][1] = ".......";num[4][2] = ".......";num[4][3] = "4.....4";num[4][4] = "4.....4";num[4][5] = "4.....4";num[4][6] = "4444444";num[4][7] = "......4";num[4][8] = "......4";num[4][9] = "......4";num[4][10] = ".......";num[5][1] = ".......";num[5][2] = ".......";num[5][3] = "5555555";num[5][4] = "5......";num[5][5] = "5......";num[5][6] = "5555555";num[5][7] = "......5";num[5][8] = "......5";num[5][9] = "5555555";num[5][10] = ".......";num[6][1] = ".......";num[6][2] = ".......";num[6][3] = "6666666";num[6][4] = "6......";num[6][5] = "6......";num[6][6] = "6666666";num[6][7] = "6.....6";num[6][8] = "6.....6";num[6][9] = "6666666";num[6][10] = ".......";num[7][1] = ".......";num[7][2] = ".......";num[7][3] = "7777777";num[7][4] = "......7";num[7][5] = "......7";num[7][6] = "......7";num[7][7] = "......7";num[7][8] = "......7";num[7][9] = "......7";num[7][10] = ".......";num[8][1] = ".......";num[8][2] = ".......";num[8][3] = "8888888";num[8][4] = "8.....8";num[8][5] = "8.....8";num[8][6] = "8888888";num[8][7] = "8.....8";num[8][8] = "8.....8";num[8][9] = "8888888";num[8][10] = ".......";num[9][1] = ".......";num[9][2] = ".......";num[9][3] = "9999999";num[9][4] = "9.....9";num[9][5] = "9.....9";num[9][6] = "9999999";num[9][7] = "......9";num[9][8] = "......9";num[9][9] = "9999999";num[9][10] = ".......";//Inum[10][1] = ".......";num[10][2] = ".......";num[10][3] = "IIIIIII";num[10][4] = "...I...";num[10][5] = "...I...";num[10][6] = "...I...";num[10][7] = "...I...";num[10][8] = "...I...";num[10][9] = "IIIIIII";num[10][10] = ".......";//Nnum[11][1] = ".......";num[11][2] = ".......";num[11][3] = "N.....N";num[11][4] = "NN....N";num[11][5] = "N.N...N";num[11][6] = "N..N..N";num[11][7] = "N...N.N";num[11][8] = "N....NN";num[11][9] = "N.....N";num[11][10] = ".......";//Fnum[12][1] = ".......";num[12][2] = ".......";num[12][3] = "FFFFFFF";num[12][4] = "F......";num[12][5] = "F......";num[12][6] = "FFFFFFF";num[12][7] = "F......";num[12][8] = "F......";num[12][9] = "F......";num[12][10] = ".......";//=num[13][1] = ".......";num[13][2] = ".......";num[13][3] = ".......";num[13][4] = ".......";num[13][5] = "=======";num[13][6] = ".......";num[13][7] = "=======";num[13][8] = ".......";num[13][9] = ".......";num[13][10] = ".......";}
void add1(int idx)
{rep(i,1,10) ans[i] += '.';rep(i,1,10) ans[i] += num[idx][i];
}
void add2(int idx)
{rep(i,1,10) ans[i] += '.';rep(i,1,10) ans[i] += unum[idx][i];
}
void dispose1(ll x)
{vector<int> nums;while(x) {nums.pb(x % 10);x /= 10;}reverse(all(nums));for(int i = 0;i < sz(nums);i ++) add1(nums[i]);
}
void dispose2(ll x)
{vector<int> nums;while(x) {nums.pb(x % 10);x /= 10;}reverse(all(nums));for(int i = 0;i < sz(nums);i ++) add2(nums[i]);add1(13);
}
void dispose3(ll x,bool lim)
{if(lim) {add1(10);add1(11);add1(12);}else dispose1(x);
}
void dispose4()
{rep(i,1,10) ans[i] += '.';
}
void solve(){rep(i,1,10) ans[i].clear();string s;ll x = 0,y = 0;cin >> s;int vis = 0;for(int i = 0;i < sz(s);i ++) {if(s[i] == '^' || s[i] == '{' || s[i] == '}') {vis ++;continue;}if(vis == 0) x = x * 10 + s[i] - '0';else y = y * 10 + s[i] - '0';}bool lim = false;dispose1(x);dispose2(y);ll tv = 1;rep(i,1,y) {if(x == 1) break;if((__int128)tv * x > 1e18) {lim = true;break;}tv *= x;}dispose3(tv,lim);dispose4();rep(i,1,10) cout << ans[i] << '\n';
}
int main()
{ios::sync_with_stdio(false);cout.tie(0),cin.tie(0);init();init2();int T = 1;cin >> T;while(T --) solve();
}H题
1.思路:找的规律
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int n;
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
int a[N];
void solve(){int n,k;cin >> n >> k;cout << n - min(2 * n,k - 1) / 2 << ' ' << n + (min(2 * n,k - 1) + 1) / 2 << endl;
}
int main()
{ios::sync_with_stdio(false);cout.tie(0),cin.tie(0);int T = 1;cin >> T;while(T --) solve();
}I题
1.思路:考虑x序列和y序列的特殊性,我们容易手搓出来最多每个格子只会被cover两次,因此我们考虑用扫描线处理这个问题,考虑答案求解,我们可以反着求答案用总数减去非纯色矩阵即可。考虑非纯色矩阵的构成,说明这个矩阵中有点被覆盖了,我们直接减去被矩形边覆盖的点数,问题转变为我们直接减去交点数即可,因此用树状数组维护一下单点修改区间查询即可。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define endl '\n'
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
pii a[N];
template <typename T>
struct Fenwick {const int n;std::vector<T> a;Fenwick (int n) : n(n), a(n + 1) {}void add(int pos, int x) {for (int i = pos; i <= n; i += i & -i) {a[i] += x;}}T query(int x) {T res = 0;for (int i = x; i; i -= i & -i) {res += a[i];}return res;}T query(int l, int r) {if (l == 0 || l > r) {return 0;}return query(r) - query(l - 1);}
};
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
void solve(){int n;read(n);rep(i,1,n) {int x1,y1,x2,y2;read(x1),read(y1);read(x2),read(y2);a[y1] = {x1,x2};a[y2] = {-x1,-x2};}Fenwick<int> fen(2 * n);ll ans = 0;rep(i,1,2*n) {int L = a[i].fi,R = a[i].se;if(L < 0) {L = -L,R = -R;fen.add(L,-1);fen.add(R,-1);}else {fen.add(L,1);fen.add(R,1);}ans = ans + 2 * n - (R - L + 1) - fen.query(2 * n) + fen.query(L,R);}cout << ans << endl;
}
int main()
{int T = 1;
// cin >> T;while(T --) solve();
}J题 不会
K题
1.思路:考虑2为质数这个特性,我们尽可能把数差为2的构造,发现无论计数情况和偶数情况我们都能够剩下2和n-1这两个数,对于2这个数我们可以插入到4和6中间,n-1这个数我们可以插入到n-3和n-5中间去。小于10的话写个dfs就行了。
2.代码实现:
#include<bits/stdc++.h>
#define sz(x) (int) x.size()
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define pii pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define ull unsigned long long
#define all(x) (x).begin(),(x).end()
#define endl '\n'
#define mp make_pair
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
inline char nc() {static char buf[1000000], *p1 = buf, *p2 = buf;return p1 == p2 && (p2 = (p1 = buf) + fread (buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
}
template <class T> inline bool read(T &x) {x = 0; char c = nc(); bool f(0);while (c < '0' || c > '9') { if (c == EOF) return false; f = c == '-', c = nc(); }while (c >= '0' && c <= '9') x = x * 10 + (c ^ 48), c = nc(); if (f) x = -x; return true;
}
struct Primes {bitset <N> st;int cnt,primes[N],idx[N],n;Primes(int n = N - 1) {this->n = n;init(n);}void init(int n) {st[0] = st[1] = 1;for(int i = 2;i <= n;i ++) {if(!st[i]) {primes[++ cnt] = i;idx[i] = cnt;}for(int j = 1;primes[j] <= n / i;j ++) {st.flip(primes[j] * i);if(i % primes[j] == 0) break;}}}//判断x是否是质数 bool isPrime(int x) {assert(x <= n);return !st[x];}//求解x在质数表是第几个 bool atIndex(int x) {assert(!st[x]);assert(x <= n);return idx[x];}
}pr(1e5);
int n,vis[11],ans[N];
inline void dfs(int f)
{if(f == n + 1) {if(pr.isPrime(abs(ans[f - 1] - ans[1]))) {rep(i,1,n) cout << ans[i] << ' ';exit(0);}return ;}rep(i,1,n) {if(!vis[i]) {if(f > 1 && !pr.isPrime(abs(i - ans[f - 1]))) continue;vis[i] = true;ans[f] = i;dfs(f + 1);vis[i] = false;}}
}
void solve(){cin >> n;//10! = 40320*9*10if(n <= 10) {dfs(1);cout << -1 << endl;return;}if(n & 1) {int cnt = 0;for(int i = 1;i <= n;i += 2) ans[++ cnt] = i;for(int i = n - 3;i >= 4;i -= 2) ans[++ cnt] = i;//剩下n-1和2int ok1 = false,ok2 = false;rep(i,1,cnt - 1) {bool same = false;if(!ok1 && pr.isPrime(abs(n - 1 - ans[i])) && pr.isPrime(abs(n - 1 - ans[i + 1]))) {ok1 = i;same = true;}if(!same && !ok2 && pr.isPrime(abs(2 - ans[i])) && pr.isPrime(abs(2 - ans[i + 1]))) {ok2 = i;}}bool same = false;if(!ok1 && pr.isPrime(abs(n - 1 - ans[cnt])) && pr.isPrime(abs(n - 1 - ans[1]))) {ok2 = n;same = true;}if(!same && !ok2 && pr.isPrime(abs(2 - ans[cnt])) && pr.isPrime(abs(2 - ans[1]))) {ok2 = n;}assert(ok1 != ok2);rep(i,1,cnt) {cout << ans[i] << ' ';if(i == ok1) cout << n - 1 << ' ';if(i == ok2) cout << 2 << ' ';}cout << endl;}else {int cnt = 0;for(int i = 1;i <= n - 3;i += 2) ans[++ cnt] = i;for(int i = n;i >= 4;i -= 2) ans[++ cnt] = i;//剩下n-1和2int ok1 = false,ok2 = false;rep(i,1,cnt - 1) {bool same = false;if(!ok1 && pr.isPrime(abs(n - 1 - ans[i])) && pr.isPrime(abs(n - 1 - ans[i + 1]))) {ok1 = i;same = true;}if(!same && !ok2 && pr.isPrime(abs(2 - ans[i])) && pr.isPrime(abs(2 - ans[i + 1]))) {ok2 = i;}}bool same = false;if(!ok1 && pr.isPrime(abs(n - 1 - ans[cnt])) && pr.isPrime(abs(n - 1 - ans[1]))) {ok2 = n;same = true;}if(!same && !ok2 && pr.isPrime(abs(2 - ans[cnt])) && pr.isPrime(abs(2 - ans[1]))) {ok2 = n;}assert(ok1 != ok2);rep(i,1,cnt) {cout << ans[i] << ' ';if(i == ok1) cout << n - 1 << ' ';if(i == ok2) cout << 2 << ' ';}cout << endl;}
}
int main()
{ios::sync_with_stdio(false);cout.tie(0),cin.tie(0);int T = 1;
// cin >> T;while(T --) solve();
}L题 不会
相关文章:
2023河南省赛vp题解
目录 A题: B题 C题 D题 E题 F题 G题 H题 I题 J题 K题 L题 A题: 1.思路:考虑暴力枚举和双hash,可以在O(n)做完。 2.代码实现: #include<bits/stdc.h> #define sz(x) (int) x.size() #define rep(i,z,…...

港科夜闻|香港科大与香港资管通有限公司签署校企合作备忘录,成立校企合作基金促科研成果落地...
关注并星标 每周阅读港科夜闻 建立新视野 开启新思维 1、香港科大与香港资管通有限公司签署校企合作备忘录,成立校企合作基金促科研成果落地。“港科资管通领航基金”28日在香港成立,将致力于推动高校科研成果转化,助力香港国际创科中心建设。…...

Neo4j 笔记
启动命令 neo4j console Cypher句法由四个不同的部分组成, 每一部分都有一个特殊的规则: start——查找图形中的起始节点。 match——匹配图形模式, 可以定位感兴趣数据的子图形。 where——基于某些标准过滤数据。 return——返回感兴趣的…...
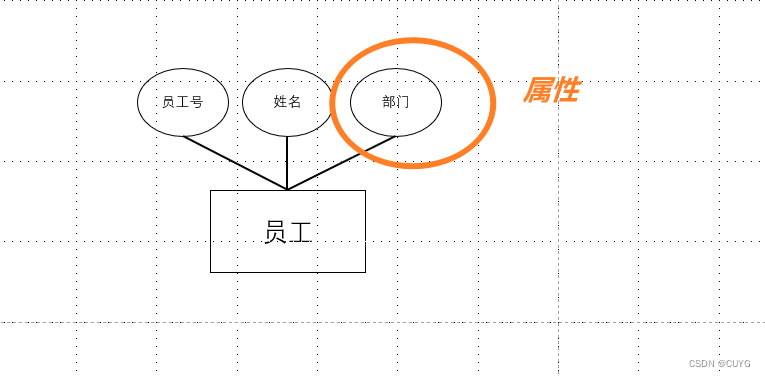
数据库基础应用——概念模型
1、实体(Entity) 客观存在并可相互区别的事物称为实体。实体可以是人、物、对象、概念、事物本身、事物之间的联系。(例如一名员工、一个部门、一辆汽车等等。) 2、属性(Attributre) 实体所具有的每个特性称为属性。(例如:员工由员…...

【学姐面试宝典】前端基础篇Ⅴ——JS深浅拷贝、箭头函数、事件监听等
前言 博主主页👉🏻蜡笔雏田学代码 专栏链接👉🏻【前端面试专栏】 今天继续学习前端面试题相关的知识! 感兴趣的小伙伴一起来看看吧~🤞 文章目录 什么是事件监听事件委托以及冒泡原理介绍一下 promise&#…...

最新研究,GPT-4暴露了缺点!无法完全理解语言歧义!
夕小瑶科技说 原创作者 |智商掉了一地、Python自然语言推理(Natural Language Inference,NLI)是自然语言处理中一项重要任务,其目标是根据给定的前提和假设,来判断假设是否可以从前提中推断出来。然而,由于…...

商业数据挖掘-第一章-数据探索式分析-1
数据探索最基本的步骤之一是获取对数据的基本描述,通过获取对数据的基本描述从而获得对数据的基本感觉。下面的一些方法用于帮助我们认识数据。 我们使用波士顿房价预测的数据集进行实验 DataFrame.describe():查看数据的基本分布,具体是对每列数据进行统计,统计值包含频…...

MybatisPlus是否防止SQL注入?
问 如果我希望使用mybatisplus同时也进行防SQL注入操作,应该怎么处理? 答 如果你想在使用 MyBatis-Plus 进行数据库操作的同时也进行防 SQL 注入处理,可以采用以下两种方式: 使用 #{} 占位符:在 QueryWrapper 或 Up…...
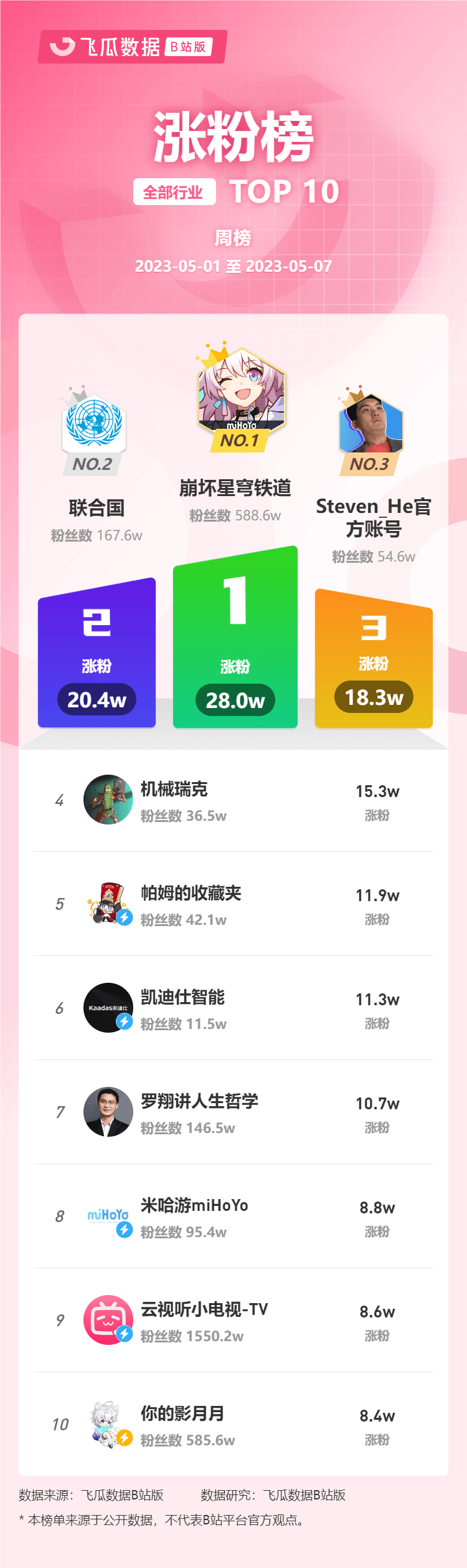
5月第1周榜单丨飞瓜数据B站UP主排行榜(哔哩哔哩平台)发布!
飞瓜轻数发布2023年5月1日-5月7日飞瓜数据UP主排行榜(B站平台),通过充电数、涨粉数、成长指数三个维度来体现UP主账号成长的情况,为用户提供B站号综合价值的数据参考,根据UP主成长情况用户能够快速找到运营能力强的B站…...

数据的插入删除和更新
在之前我们就已经学过了数据的插入,在这里再进行一点内容的补充: 在insert语句中,value子句中参数的顺序与表中各个列的顺序是一一对应的。 mysql> insert into first_table(second_column, first_column) values(aaa, 1); Query OK, 1 r…...

C# byte[] 与 int 类型互转
本文讲述在C#中,怎样使用 BitConverter 类将字节数组转换为 int 然后又转换回字节数组的过程。 为什么需要这样呢?这是因为,比如说,在从网络读取字节之后,可能需要将字节转换为内置数据类型。 除了示例中的 ToInt32(Byte[], Int32) 方法之外…...

MySQL---多表联合查询(上)(多表关系、外键约束、学生成绩多表关系、交叉连接查询)
1. 多表关系 MySQL多表之间的关系可以概括为: 一对一: 比如:一个学生只有一张身份证;一张身份证只能对应一学生。 实现原则:在任一表中添加唯一外键,指向另一方主键,确保一对一关系。 一般一对…...

【iOS】—— RunLoop线程常驻和线程保活
文章目录 没有线程常驻会怎么样? 线程常驻线程保活 没有线程常驻会怎么样? 我们一般写一个子线程,子线程执行完分配的任务后就会自动销毁,比如下面这个情况: 我们先重写一下NSThread里面的dealloc方法,打印…...
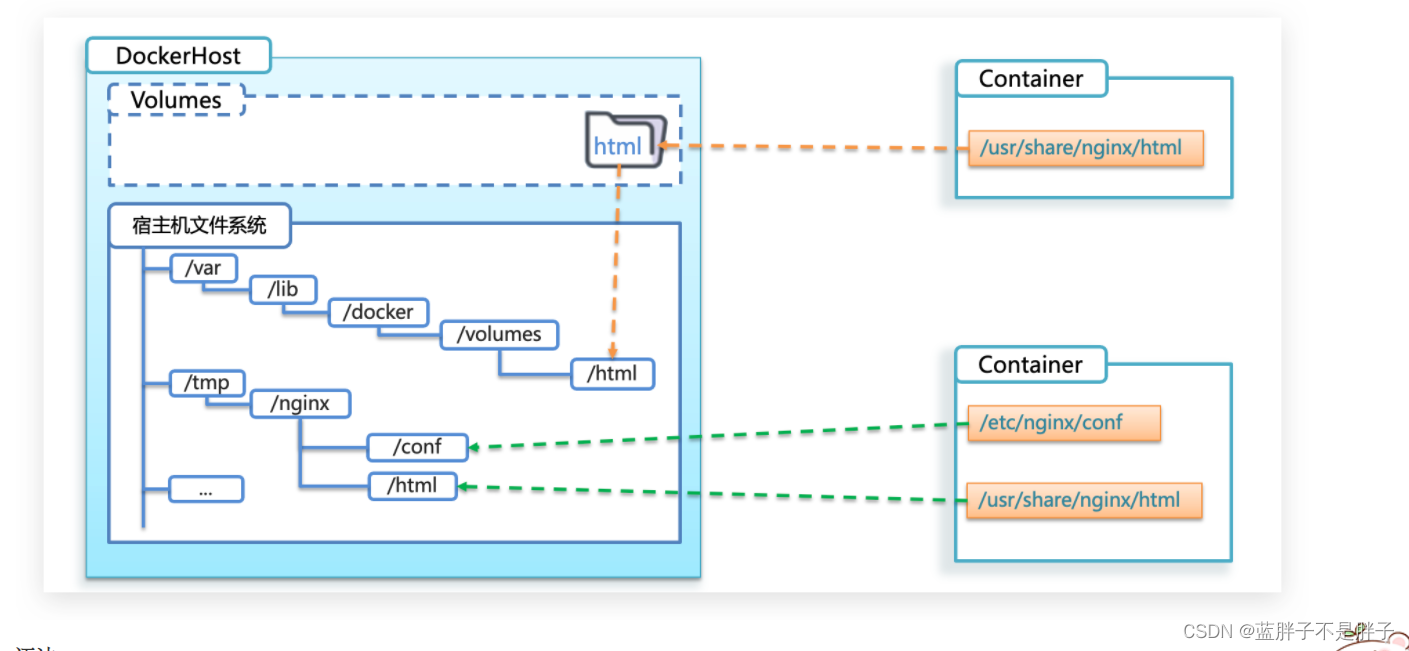
Springcloud--docker快速入门
认识docker docker相关操作 1.初识Docker 1.1.什么是Docker 微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。 分布式系统中,依赖的组件非常多,不同组件之间部署时往往会产生一些冲突。在数百上千台服务中重复部署…...
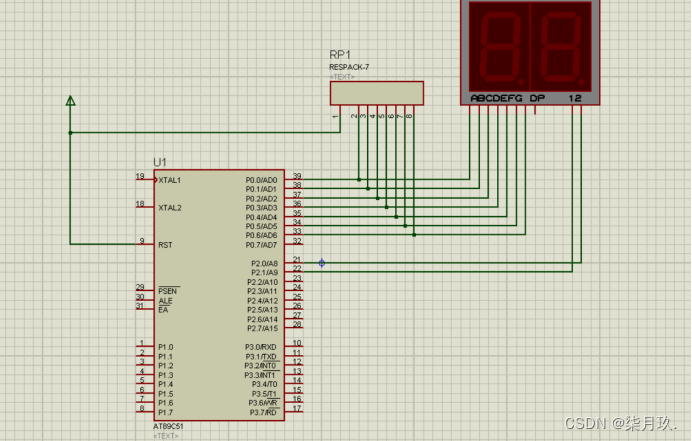
基于AT89C51单片机的电子计数器设计与仿真
点击链接获取Keil源码与Project Backups仿真图: https://download.csdn.net/download/qq_64505944/87770826 源码获取 主要内容: 设计一个电子计时器,数码管初始显示值为“00”,每隔1s电子秒表加1;秒计数到60时清0&a…...

IT程序员如何面对35岁大龄问题?我从公司老板的角度聊聊
很多从事IT行业的人一想到35岁就很焦虑,担心自己被公司裁员后找不到工作。同时还有家庭责任加身,担心中年失业后晚年生活。作为一位公司老板,我想从我的角度谈一下这个问题。 首先,我本质上不介意我的员工年龄,无论是…...

【计算机专业漫谈】【计算机系统基础学习笔记】W2-2-2 模运算系统和补码表示
利用空档期时间学习一下计算机系统基础,以前对这些知识只停留在应试层面,今天终于能详细理解一下了。参考课程为南京大学袁春风老师的计算机系统基础MOOC,参考书籍也是袁老师的教材,这是我的听课自查资料整理后的笔记 补码表示法…...

vue概述
vue2和vue3的区别 vue2和vue3区别 NOvue2vue31 optinos Api写法 比较分散 Compostiton Api 代码集 2重写数序双向绑定通过Object.defineProperty()实现 基于Proxy实现 对数组有了更好的支持 3Fragments 1,在template中只能一个div 2…...
SpringCloud-OpenFeign案例实战
关于Spring Cloud Open Feign的介绍可以参考这两篇博客 OpenFeign服务接口调用 使用Feign作为服务消费者 本博客参考gitee开源项目代码,结合自己的理解,记录下微服务场景下的使用。Talk is cheap. Show me the code! 一、项目结构 这里使用…...

ACM - 数学 - 提高(还没学多少)
ACM - 数学 练习题 一、数论1、分解质因数 :AcWing 197. 阶乘分解2、求约数个数(1)AcWing 1294. 樱花 (求 n!约数个数之和)(2)AcWing 198. 反素数 (求 1 ~ N 中约数最多的…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
