可拓展哈希
可拓展哈希
借CMU 15445的ppt截图来说明问题。
我们传统静态hash的过程是hash函数后直接将值存入对应的bucket,但是在可扩展hash中,得查询Directory(左),存入directory指向的bucket(右)。
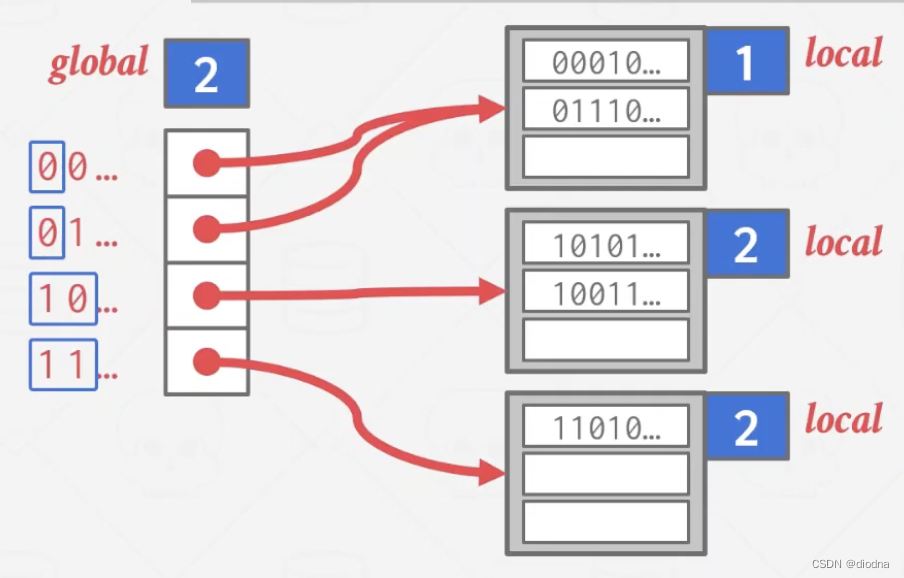
下面我们存放key=B,哈希值为hash(B),查询directory知道要放到第二个bucket中。
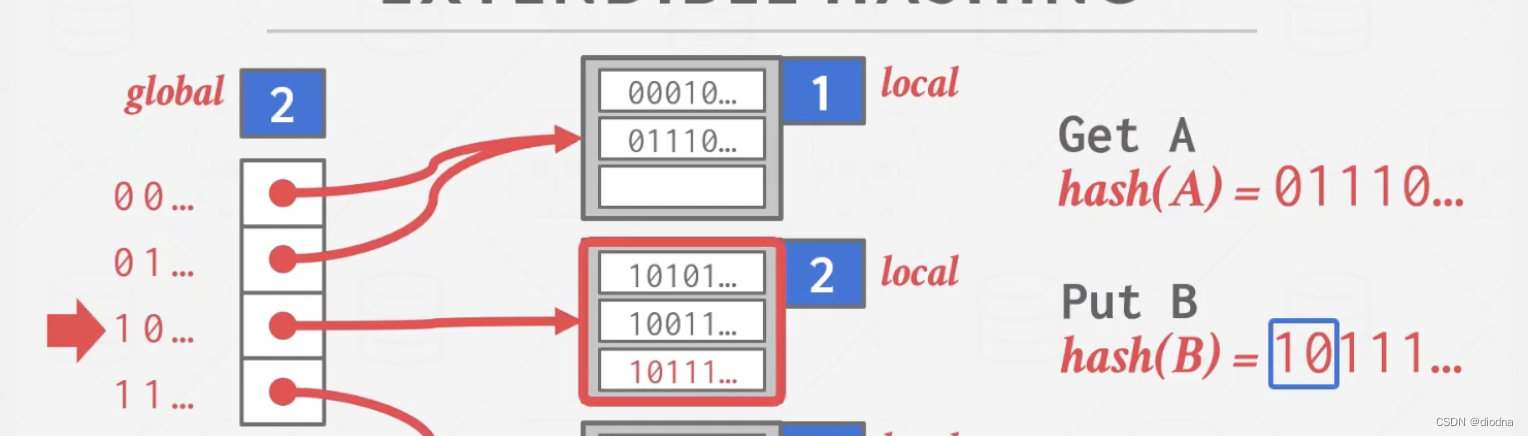
然后再放一个key=C(hash( C)的值被老师的视频挡住了,就不放图片了),哈希值为hash( C),并且hash( C)高两位也是10,查询directory也要放到第二个bucket,但此时bucket满了,就将该bucket分裂,其他bucket不用变动,那么directory应该怎么变动呢?分为两种情况(先说明此时hash( C)对应第2种情况)
- bucket的local depth < global depth:分裂bucket,改变directory中指向该bucket的指针,让他们分别指向分裂出来的两个bucket,并且这两个bucket的local depth+1
- bucket的local depth = global depth:分裂bucket,将directory的大小*2,并且重新分配directory中的指针(这里不知道怎么描述比较好,可以结合下面的图来理解),并且分裂后的两个bucket的local depth+1,global depth+1
很明显hash©对应上面的情况2,因此结果如下:
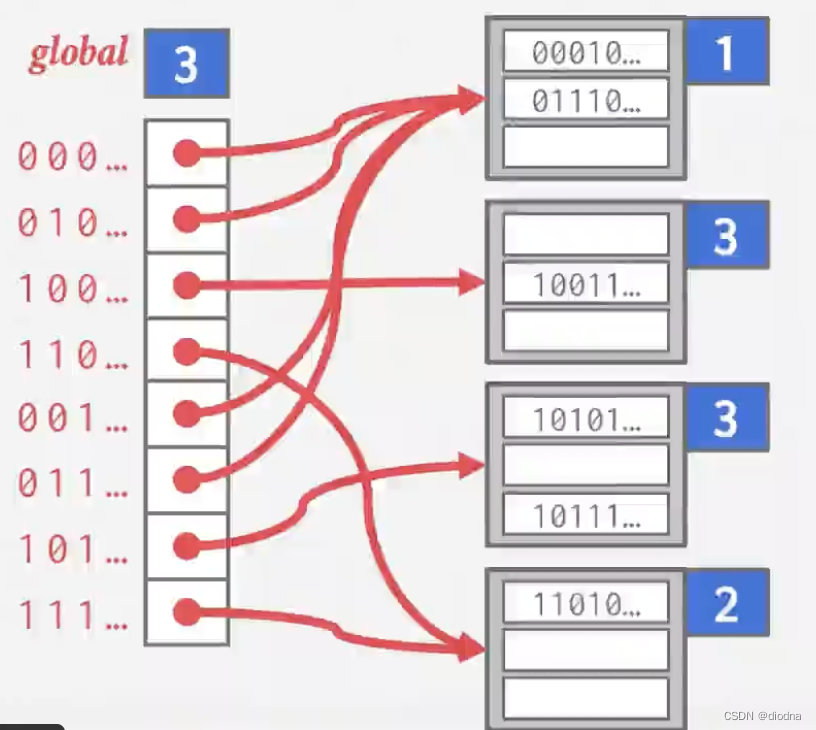
第一种情况在课件中没有提到,我也做一下说明(懒得画图了)。我们先回到这张图,基于现在这个状态分析第一种情况:
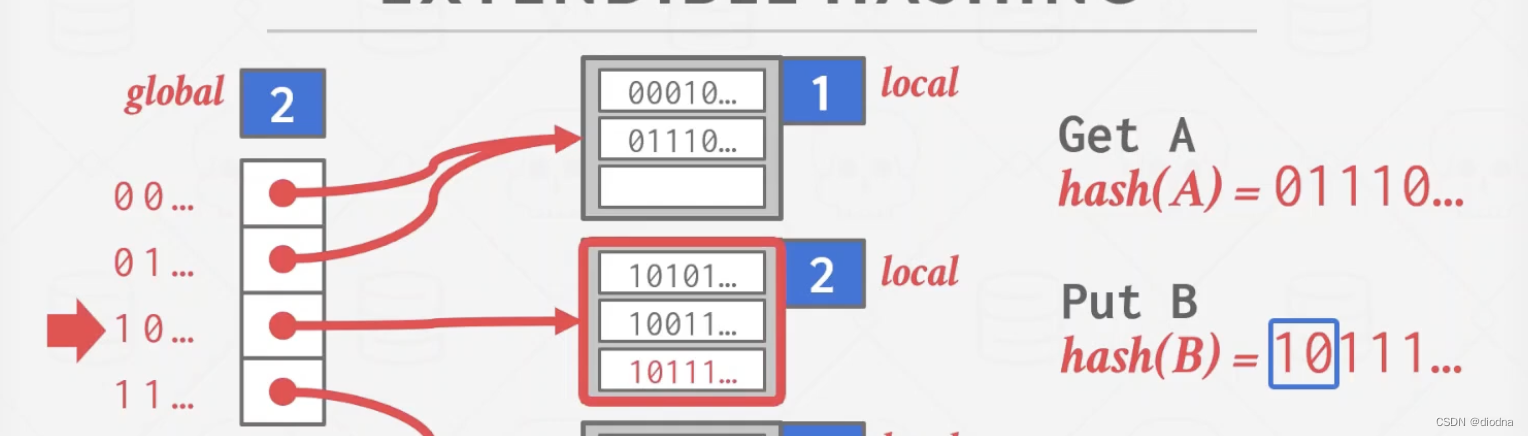
假设现在第一个bucket是满的(我们这里假设bucket中第三个为01…),然后hash©=00…,要插入第一个bucket,那么根据情况1,我们将bucket分裂为两个bucket,directory不用增长,但是00…和01…指针分别要指向第一个分裂的bucket和第二个分裂的bucket,第一个分裂桶存放了两个01…,第二个分裂桶存放了两个00…
如果还是不懂的话,可以多看几遍上述操作过程或者看下面的参考链接
简单的体会总结:可拓展哈希好处在于某个桶分裂的时候,不用移动其他桶的元素,减少开销。存在的问题很明显,如果多次插入的hash值相同,分裂肯定是不可行的,因为无论怎么分裂,这几个相同hash值都在同一个bucket中,因此需要用overflow bucket的方式来“打补丁”了,所以最基本的可拓展哈希算法不能直接拿来用,得做点变种吧,不过思想值得学习。
参考链接:
https://blog.csdn.net/qq_37026934/article/details/125368237
https://www.bilibili.com/video/BV1xa41137S4?p=7&vd_source=65dfb8ffc4e0d60f317dcde5b6ceb9fd
https://zhuanlan.zhihu.com/p/375039823
相关文章:

可拓展哈希
可拓展哈希 借CMU 15445的ppt截图来说明问题。 我们传统静态hash的过程是hash函数后直接将值存入对应的bucket,但是在可扩展hash中,得查询Directory(左),存入directory指向的bucket(右)。 下面…...

Java 版 spring cloud 工程系统管理 +二次开发 工程项目管理系统源码
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

通过伴随矩阵怎么求逆矩阵
设矩阵A为n阶方阵,其伴随矩阵为Adj(A),则A的逆矩阵为: A⁻ (1/|A|) Adj(A) |A|为A的行列式 Adj(A)为A的伴随矩阵 具体步骤如下: 求出A的行列式|A| 求出A的伴随矩阵 Adj(A) 。伴随矩阵的定义为:对于A的第i行第j列…...

巡检机器人之仪表识别系统
作者主页:爱笑的男孩。 博客简介:分享机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。 如发现文章有误,麻烦请指出,我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666foxmail.c…...
)
面试官反感的求职者(下)
上期给大家总结了面试中常见的一些问题,今天就接着上次的话题再给大家说说HR反感的求职者,希望同学们可以自省,避免踩雷。小编从如信银行考试中心了解到的有: 第一、缺乏个性者 这种考生在答题中往往表现得千篇一律,从…...
-生存曲线(LM曲线)(补充篇))
可视化绘图技巧100篇分析篇(二)-生存曲线(LM曲线)(补充篇)
目录 前言 知识储备 生存分析中的基本概念 生存分析 (survival analysis) 事件 (event)...

【100%通过率 】【华为OD机试python】钟表重合时刻【 2023 Q1考试题 A卷|100分】
华为OD机试- 题目列表 2023Q1 点这里!! 2023华为OD机试-刷题指南 点这里!! ■ 题目描述 钟表是日常生活中不可缺少的时间度量计, 其时针、分针、秒针三者的转动速度满足特定规律(见备注)。 现在输入时刻 time ,请计算出时刻 time 小时和 time+1 小时之间, 时针和分针…...

Java线程池编码示例
第1步:自定义线程实现类 Java中多线程编码时,定义线程类有两种方式: 继承Thread类实现Runnable接口(由于Java的单继承特性,一般推荐使用此方式) public class BizThread implements Runnable {private int …...

如何优化Android 4.x系统设置字体大小
android4.x系统设置字体大小导致应用布局混乱的解决方案 在前几年,Android系统的设置界面还是相对简单的,用户可以通过设置菜单进行各种系统设置,如字体大小、壁纸、铃声等。但是随着用户对系统功能的需求越来越多,Android系统也在…...
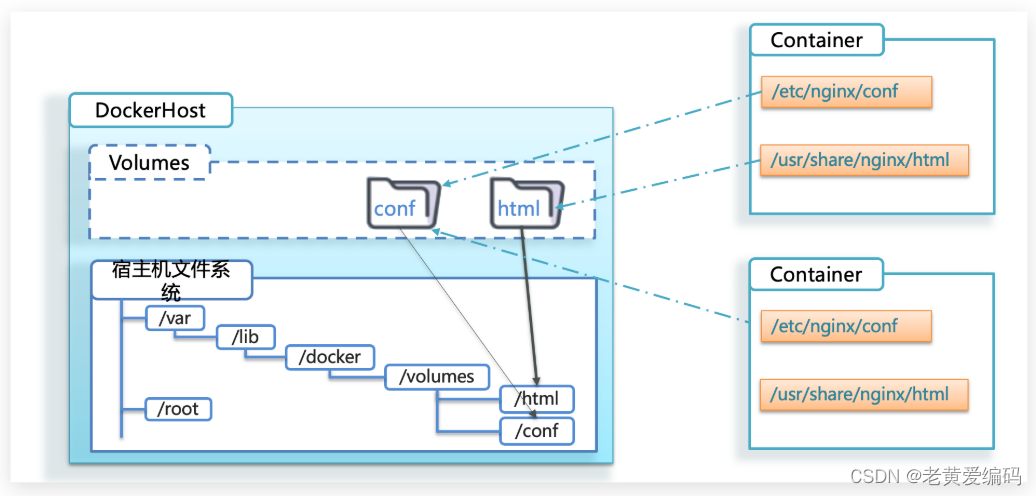
Docker安装、Docker基本操作
一、Dokcer安装 1.安装 # 1、yum 包更新到最新,需要几分钟时间(注意:也可以直接跨过) sudo yum update # 2、作用:安装需要的软件包, yum-util 提供yum-config-manager功能,另外两个是devicemapper驱动依赖的 sudo yum install -y yum-util…...

系统集成项目管理工程师知识点总结
项目经理的五种权利: 职位权力: 来源于管理者在组织中的职位和职权。罚权力: 使用降职、扣薪、惩罚、批评、威胁等负面手段的能力。奖励权力: 给予下属奖励的能力专家权力: 来源于个人的专业技能。参照(号…...

【游戏里的网络同步分析】马里奥制造2 多人模式
前置知识 先说几个游戏设计的术语。 PlayerAgent是玩家控制的网络游戏中的角色形象,也是代表在游戏空间中的玩家,被唯一PlayerController所拥有,被所有用户可观测到。 在马里奥制造2中,PlayerAgent一共有四种:马里奥 …...

SSM框架学习-注解开发第三方bean管理
1. 复习xml配置文件管理第三方bean 在Spring中,可以使用依赖注入(Dependency Injection)来管理和使用第三方Bean。Spring提供了多种方式来进行依赖注入,比如构造函数注入、Setter方法注入、字段注入等。下面以Setter方法注入为例&…...
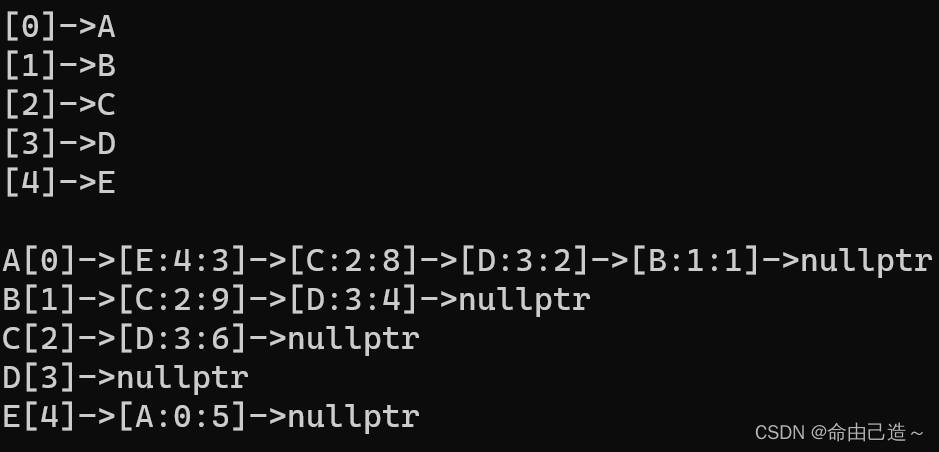
【数据结构与算法】图——邻接表与邻接矩阵
文章目录 一、图的基本概念二、图的存储结构2.1 邻接矩阵2.2 邻接表2.3 邻接矩阵的实现2.4 邻接表的实现 三、总结 一、图的基本概念 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E&#…...

网安笔记02 密码学基础
密码学概述 • 1.1、密码学的基本概念 密码编码学 : 密码编制 密码分析学 : 密码破译 密码学 : 研究密码保护 通信手段的科学, 密码编码学密码分析学 密码技术: 把可理解的消息伪装为不可理解的消息,再复原成原消息的科学 概…...

open3d io操作
目录 1. read_image, write_image 2. read_point_cloud, write_point_cloud 3. 深度相机IO操作 4. Mesh文件读取 1. read_image, write_image 读取jpg. png. bmp等文件 image_io.py import open3d as o3dif __name__ "__main__":img_data o3d.data.JuneauIma…...
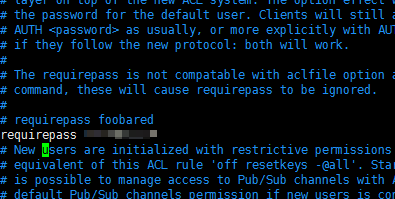
【Linux】Linux安装Redis(图文解说详细版)
文章目录 前言第一步,下载安装包第二步,上传安装包到/opt下(老规矩了,安装包在opt下)第三步,解压安装包第四步,编译第五步,安装第六步,配置redis第七步,设置开…...

setTimeout不准时,CSS精准实现计时器功能
实际开发过程中,我们会经常遇到,首次进入页面进行相应提示,然后指定时间后自动消失或者前端时钟展示等需求。 按照传统方案,我们可以使用 setTimeout 实现。但其存在:实际延时比设定值更久的情况。 setTimeout 不准时…...

单细胞跨模态分析综述
单细胞技术的最新进展使跨模态和组织位置的细胞高通量分子分析成为可能。单细胞转录组数据现在可以通过染色质可及性、表面蛋白表达、适应性免疫受体库分析和空间信息进行补充。跨模态单细胞数据的可用性越来越高,推动出新的计算方法,以帮助科学家获得生…...
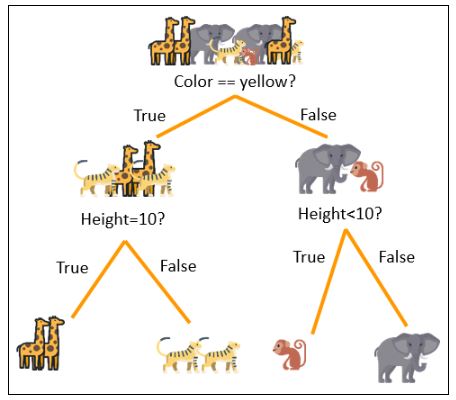
【零基础学机器学习 1】什么是机器学习?
机器学习的社会应用 1. 金融风控 机器学习在金融风控方面的应用非常广泛,可以用于预测借款人的信用风险、欺诈行为等。通过收集大量的历史数据,构建机器学习模型,可以对借款人的信用风险进行预测,从而帮助金融机构降低风险。 2…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
