图神经网络:在KarateClub数据集上动手实现图神经网络
文章说明:
1)参考资料:PYG官方文档。超链。
2)博主水平不高,如有错误还望批评指正。
3)我在百度网盘上传了这篇文章的jupyter notebook。超链。提取码8888。
文章目录
- 文献阅读:
- 代码实操:
文献阅读:
参考文献:SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
中文翻译:用图神经网络进行半监督的分类
我在百度网盘上传这篇文献。超链。提取码8888。
文献首先:介绍了其他前辈的工作。在损失函数中使用拉普拉斯正则化项。公式如下(打这个公式真费劲,还的学Latex): L = L 0 + λ L r e g \mathcal{L}=\mathcal{L}_{0}+\lambda\mathcal{L}_{reg} L=L0+λLreg with L r e g = ∑ i , j A i , j ∣ ∣ f ( X i ) − f ( X j ) ∣ ∣ 2 = f ( X ) T Δ f ( X ) \mathcal{L}_{reg}=\sum_{i,j}{A}_{i,j}||\mathcal{f}({X}_{i})-\mathcal{f}({X}_{j})||^{2}=\mathcal{f}(X)^{T}\Delta\mathcal{f}(X) Lreg=∑i,jAi,j∣∣f(Xi)−f(Xj)∣∣2=f(X)TΔf(X)
符号说明: L \mathcal{L} L表示为损失函数。 L 0 \mathcal{{L}_{0}} L0表示为有标签的损失(还有没标签的毕竟是半监督)。 λ \lambda λ表示为权重系数。 A i , j {A_{i,j}} Ai,j表示为图边。 f ( ⋅ ) \mathcal{f}(\cdot) f(⋅)表示为像神经网络的可微函数。 X X X表示为特征矩阵。 Δ = D − A \Delta=D-A Δ=D−A表示为非规范化的拉普拉斯算子。 D D D表示为度的矩阵, D i , i = ∑ j A i , j D_{i,i}=\sum_{j}A_{i,j} Di,i=∑jAi,j。
文章然后:简单说明使用上述公式需要有个假设:图中连接节点共享相同标签。于是作者这篇文章便就来了,为了解决这个问题,使用神经网络模型 f ( X , A ) f(X,A) f(X,A)编码图结构,避免使用显示基于图正则化。文章有两贡献,1.提出一种简单良好直接作用于图上的神经网络传播规则并且展示它是如何从谱图卷积的一阶逼近得到反馈。2.演示了基于图神经网络是如何分类的。
文章然后:具体开始阐述理论。 H l + 1 = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H l W l ) H^{l+1}=\sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{l}W^{l}) Hl+1=σ(D~−21A~D~−21HlWl)。(知道核心公式就好,其他细节我们跳过因为我看不懂)
符号说明: D i , i = ∑ j A i , j D_{i,i}=\sum_{j}A_{i,j} Di,i=∑jAi,j表示为度的矩阵。 A ~ = A + I N \tilde{A}=A+I_{N} A~=A+IN表示为邻接矩阵加上一个单位矩阵。 W l W^{l} Wl表示为权重系数。 σ \sigma σ表示为激活函数。 H l H^{l} Hl为第 l l l层的特征矩阵。 H 0 H^{0} H0即为 X X X。
文章然后:进行代码分类实操,他们这里搭建了两层GCN。所以最后的公式为 Z = f ( X , A ) = s o f t m a x ( A ^ R e l u ( A ^ X W 0 ) W 1 ) Z=f(X,A)=softmax(\widehat{A}Relu(\widehat{A}XW^{0})W^{1}) Z=f(X,A)=softmax(A Relu(A XW0)W1)。这里 A ^ = D ~ − 1 2 A ~ D ~ − 1 2 \widehat{A}=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} A =D~−21A~D~−21。损失函数就使用交叉熵 L = − ∑ l ∈ Y l ∑ f = 1 F Y l f ln Z l f L=-\sum_{l \in \mathcal{Y}_{l}}\sum_{f=1}^FY_{lf}\ln{Z_{lf}} L=−∑l∈Yl∑f=1FYlflnZlf吧。
文章然后:介绍图半监督学习领域以及图上运行神经网络领域两个领域相关工作。
文章然后:进行实验展示结果。
文章然后:进行讨论。1.作者模型可以克服Skip-gram方法难以优化多步流程限制同时时间以及效果表现更好。2.未来工作1)解决内存:作者证明对于无法使用GPU大型图,用CPU是可行的。用小批量随机梯度可以缓解这个问题。但是生成小批量时应该考虑GCN的层数,对于非常大且密集连接的图可能需要进一步地近似。2)不支持有向图,但是有解决方法的(具体是什么我没看懂)3)考虑一个权衡参数 λ \lambda λ可能会有益。具体来说就是修改生成自循环图时用的 λ \lambda λ。即 A ~ = A + λ I \tilde{A}=A+\lambda I A~=A+λI。
文章然后:得到结论。
文章最后:引用以及其他工作。1)WL-1算法2)深层的GCN。太深不好。
PS:以上仅是我的理解,我的理解可能不对。然后关于这个GCN以及WL算法,有两篇文章研究了它们,还是挺有趣的。我在百度网盘上传了这连篇文章。超链。提取码8888。
代码实操:
导入对应的库
import matplotlib.pyplot as plt
import networkx as nx
定义可视化的函数
def visualize_graph(G,color):plt.figure(figsize=(7,7))plt.xticks([])plt.yticks([])nx.draw_networkx(G,pos=nx.spring_layout(G,seed=42),with_labels=False,node_color=color,cmap="Set2")plt.show()
#可视化图网络
def visualize_embedding(h,color,epoch=None,loss=None):plt.figure(figsize=(7,7))plt.xticks([])plt.yticks([])h=h.detach().cpu().numpy()plt.scatter(h[:,0],h[:,1],s=140,c=color,cmap="Set2")if epoch is not None and loss is not None:plt.xlabel(f'Epoch: {epoch}, Loss: {loss.item():.4f}',fontsize=16)plt.show()
导入对应的库:数据集1
from torch_geometric.datasets import KarateClub
dataset=KarateClub()
KarateClub数据集简单说明:34个人的社交网络,如果在俱乐部之外两人认识连一条边。然后由于俱乐部的内部冲突,人们选择站队所以分成两派。
打印数据集的信息
print(len(dataset),dataset.num_features,dataset.num_classes)
#输出:1 34 4
简单说明:num_features:33加上1。33指,这个节点与其他的33个节点是否有边,有边为1,无边为0。1是指度。num_classer:按理应该为2,但是官方做了修改,所以为4。
data=dataset[0]
#具体到确定的图上
print(data.num_nodes,data.num_edges,data,data.train_mask.sum().item())
#输出:34 156 Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34]) 4
print(data.has_isolated_nodes(),data.has_self_loops(),data.is_undirected())
#输出:False False True
edge_index=data.edge_index
print(edge_index.t())
#输出:不表
导入对应的库
from torch_geometric.utils import to_networkx
可视化图网络
G=to_networkx(data,to_undirected=True)
visualize_graph(G,color=data.y)

搭建模型GCN的框架
from torch_geometric.nn import GCNConv
from torch.nn import Linear
import torch
class GCN(torch.nn.Module):def __init__(self):super().__init__()self.conv1=GCNConv(dataset.num_features,4)self.conv2=GCNConv(4,4)self.conv3=GCNConv(4,2)self.classifier=Linear(2,dataset.num_classes)def forward(self,x,edge_index):h=self.conv1(x,edge_index)h=h.tanh()h=self.conv2(h,edge_index)h=h.tanh()h=self.conv3(h,edge_index)h=h.tanh()out=self.classifier(h)return out,h
model=GCN()
print(model)
#输出
#GCN(
# (conv1): GCNConv(34, 4)
# (conv2): GCNConv(4, 4)
# (conv3): GCNConv(4, 2)
# (classifier): Linear(in_features=2, out_features=4, bias=True)
#)
简单说明: X v ( l + 1 ) = W ( l + 1 ) ∑ w ∈ N ( v ) ∪ { v } 1 c w , v ⋅ X w ( l ) X_{v}^{(l+1)}=W^{(l+1)}\sum_{w \in N(v)\cup{\{v\}}}\frac{1}{c_{w,v}}\cdot X_{w}^{(l)} Xv(l+1)=W(l+1)∑w∈N(v)∪{v}cw,v1⋅Xw(l)
可视化图嵌入(这里只有正向传播)
model=GCN()
_,h=model(data.x,data.edge_index)
visualize_embedding(h,color=data.y)

进行训练得出结果
model=GCN()
criterion=torch.nn.CrossEntropyLoss()
optimizer=torch.optim.Adam(model.parameters(),lr=0.01)
def train(data):optimizer.zero_grad()out,h=model(data.x,data.edge_index)loss=criterion(out[data.train_mask],data.y[data.train_mask])loss.backward()optimizer.step()return loss,h
for epoch in range(401):loss,h=train(data)if epoch==400:visualize_embedding(h,color=data.y,epoch=epoch,loss=loss)

相关文章:

图神经网络:在KarateClub数据集上动手实现图神经网络
文章说明: 1)参考资料:PYG官方文档。超链。 2)博主水平不高,如有错误还望批评指正。 3)我在百度网盘上传了这篇文章的jupyter notebook。超链。提取码8888。 文章目录 文献阅读:代码实操: 文献阅读: 参考文…...

ArduPilot之开源代码调试技巧
ArduPilot之开源代码调试技巧 1. 源由2. ArduPilot Code Debugging Part13. ArduPilot Code Debugging Part24. 持续更新中。。。5. 参考资料 1. 源由 对于如何调试和验证ArduPilot,对于新手来说,有的时候反而是入门的一个门槛。 其实这个并不难&#…...

Linux网络基础-2
在之前的网络基础博客中,我们对网络的基本概念进行了一个简单的介绍,那么接下来的网络内容中,我们将对网络通信中的典型协议进行详细解释。 我们根据网络协议中的分层来对典型协议进行注意介绍,不过对于物理层的传输我们不做考究…...

软件测试报告模板
目录 2 1 概述... 3 1.1 测试目的... 3 1.2 测试策略... 3 1.3 测试方法... 3 1.4 计划验收标准... 3 1.5 测试用例... 4...
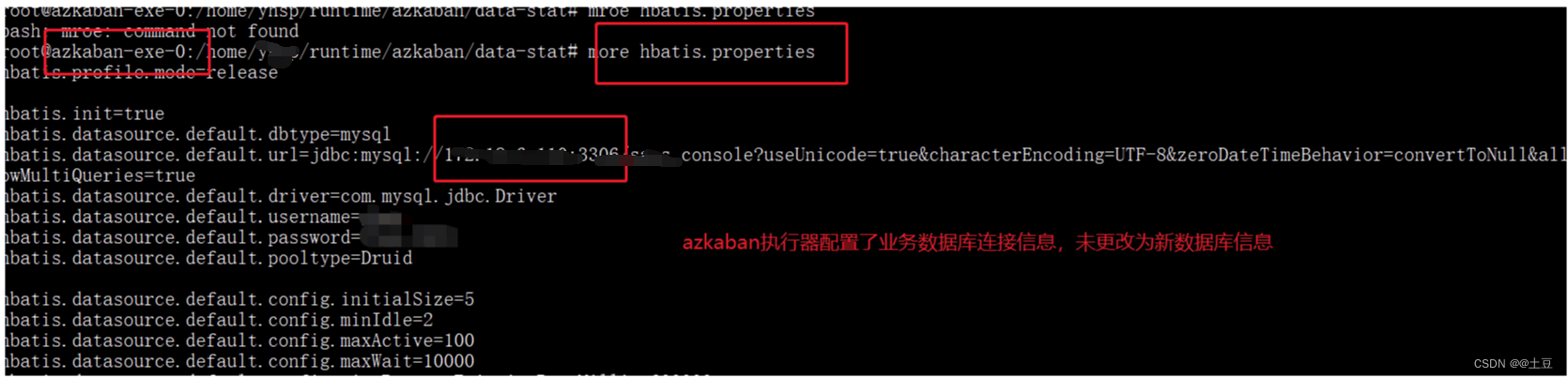
记一次azkaban调度异常处理
一、背景 预发布环境使用的数据库性能比较低,根据业务测试的需求,需要将数据库更换成 稳定高性能的数据库。更换业务数据库后azkaban定时任务失败 二、数据库服务信息 说明:该部分使用代号来代替,非真实信息 该数据库存储了azka…...

开发一个vue自定义指令的npm库-系列三:使用rollup打包npm库并发布
配置 rollup 使用rollup将 TypeScript 代码转换为 JavaScript,然后进行压缩和输出到目标文件。 项目根目录新建rollup.config.js import typescript from "rollup/plugin-typescript"; import terser from "rollup/plugin-terser"; import de…...
C嘎嘎的运算符重载基础教程以及遵守规则【文末赠书三本】
博主名字:阿玥的小东东 大家一起共进步! 目录 基础概念 优先级和结合性 不会改变用法 在全局范围内重载运算符 小结 本期送书:盼了一年的Core Java最新版卷Ⅱ,终于上市了 基础概念 运算符重载是通过函数重载实现的…...
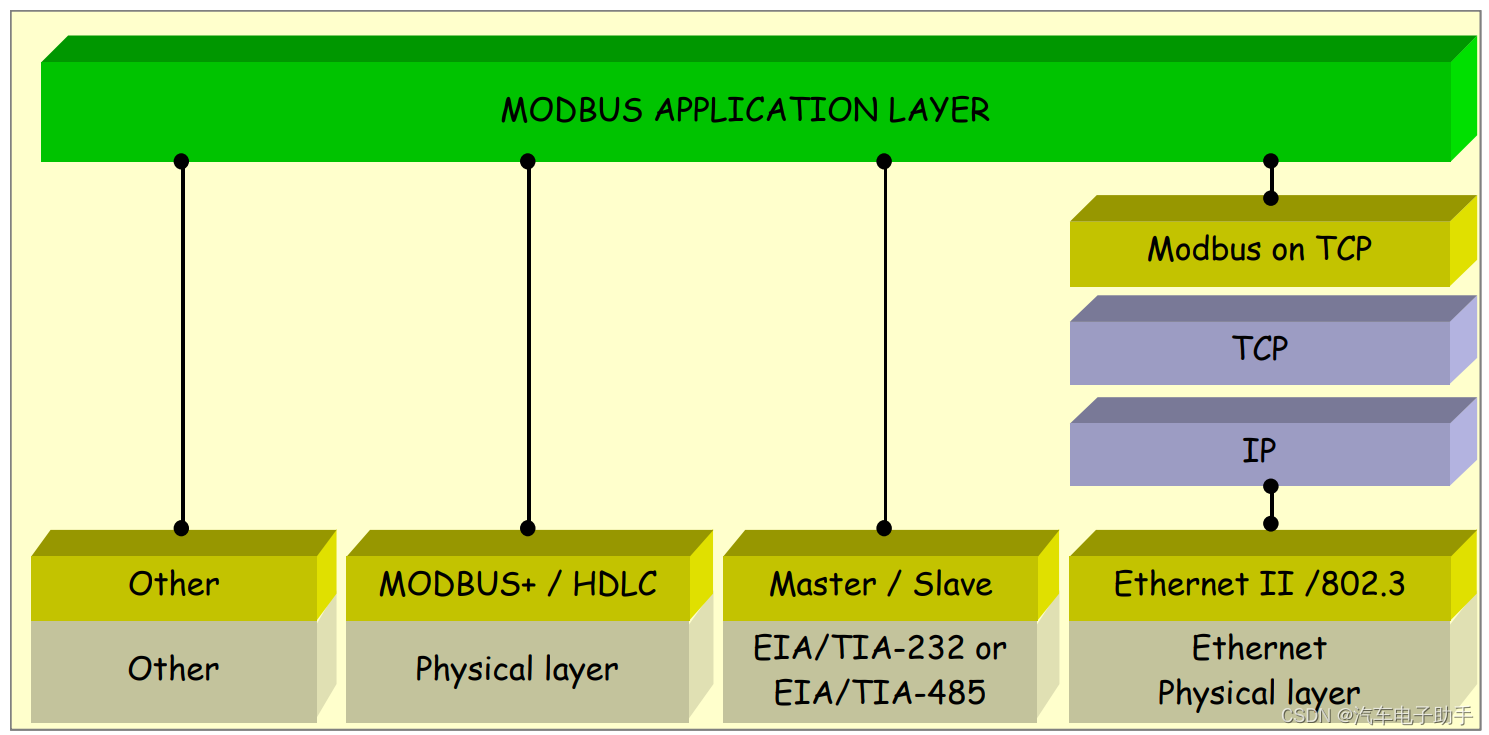
【MCAL_UART】-1.2-图文详解RS232,RS485和MODBUS的关系
目录 1 UART,RS232和RS485通信拓扑 2 什么是RS232 2.1 RS232标准的演变 2.2 RS232标准讲了哪些 2.2.1 RS232通信的电平 2.2.2 RS232通信的带宽 2.2.3 RS232通信距离 2.2.4 RS232通信的机械接口 3 什么是RS485 3.1 RS485标准的演变 3.2 RS485标准讲了哪些…...
——单例模式)
设计模式详解(二)——单例模式
单例模式简介 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式,创建型模式是一类最常用的设计模式,在软件开发中应用非常广泛,它提供了一种创建对象的最佳方式。 单例模…...
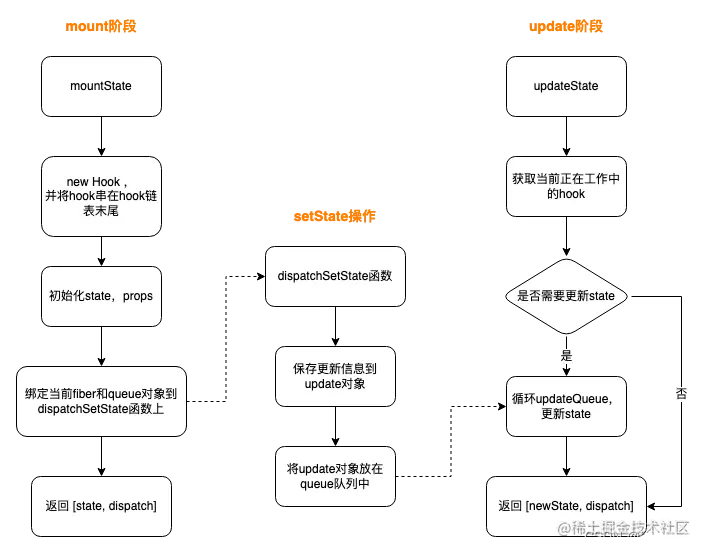
为什么hooks不能在循环、条件或嵌套函数中调用
hooks不能在循环、条件或嵌套函数中调用 为什么? 带着疑问一起去看源码吧~ function App() {const [num, setNum] useState(0);const [count, setCount] useState(0);const handleClick () > {setNum(num > num 1)setCount(2)}return <p …...

互联网赚钱项目有哪些?目前最火的互联网项目
互联网是一个神奇的行业,大门不出二门不迈,一根网线一台电脑,甚至一台手机就可以赚钱。它给我们创造了前所未有的商业机会,让成千上万有梦想,敢想敢干的人通过互联网获得了巨大的成功!正因为如此࿰…...

队列、栈专题
队列、栈专题 LeetCode 20. 有效的括号解题思路代码实现 LeetCode 921. 使括号有效的最少添加解题思路代码实现 LeetCode 1541. 平衡括号字符串的最少插入次数解题思路代码实现 总结 不要纠结,干就完事了,熟练度很重要!!ÿ…...

TensorFlow vs PyTorch:哪一个更适合您的深度学习项目?
在深度学习领域中,TensorFlow 和 PyTorch 都是非常流行的框架。这两个框架都提供了用于开发神经网络模型的工具和库,但它们在设计和实现上有很大的差异。在本文中,我们将比较 TensorFlow 和 PyTorch,并讨论哪个框架更适合您的深度…...

大项目环境配置
目录 Linux的龙蜥8是什么? OpenGL是什么? 能讲讲qt是什么吗? 我可以把qt技术理解为c工程师的前端开发手段吗? 我其实一直有些不懂大家所说的这个开发框架啥的,这个该如何理解呢 那现在在我看来,框架意…...

Elasticsearch——》正则regexp
推荐链接: 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

五面阿里Java岗,从小公司到阿里的面经总结
面试 笔试常见的问题 面试常见的问题下面给的面试题基本都有。 1 手写代码:手写代码一般会考单例、排序、线程、消费者生产者 排序。 2 写SQL很常考察group by、内连接和外连接 2.面试1-5面总结 1)让你自我介绍 2)做两道算法…...
redis(7)
全局ID生成器: 全局ID生成器,是一种在分布式系统下用来生成全局唯一ID的工具,一般要满足以下特性 唯一性高可用(随时访问随时生成)递增性安全性(不能具有规律性)高性能(生成ID的速度快) 为了增加ID的安全性,我们不会使用redis自增的数值&am…...

互联网从业者高频单词 300个
测试 (Test) 软件 (Software) 用例 (Test Case) 缺陷 (Defect) 提交 (Submit) 回归测试 (Regression Testing) 验收测试 (Acceptance Testing) 单元测试 (Unit Testing) 集成测试 (Integration Testing) 性能测试 (Performance Testing) 负载测试 (load Testing) 压…...

初始化vue中data中的数据
当组件的根元素使用了v-if的时候, 并不会初始化data中的数据 如果想完全销毁该组件并且初始化数据,需要在使用该组件的本身添加v-if 或者是手动初始化该组件中的数据 初始化化数据的一些方法 Object.assign(this.$data, this.$options.data()) this.$data:当前的da…...

神经网络的建立-TensorFlow2.x
要学习深度强化学习,就要学会使用神经网络,建立神经网络可以使用TensorFlow和pytorch,今天先学习以TensorFlow建立网络。 直接上代码 import tensorflow as tf# 定义神经网络模型 model tf.keras.models.Sequential([tf.keras.layers.Dense…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
