Python基础学习笔记 —— 数据结构与算法
数据结构与算法
- 1 数据结构基础
- 1.1 数组
- 1.2 链表
- 1.3 队列
- 1.4 栈
- 1.5 二叉树
- 2 排序算法
- 2.1 冒泡排序
- 2.2 快速排序
- 2.3 (简单)选择排序
- 2.4 堆排序
- 2.5 (直接)插入排序
- 3 查找
- 3.1 二分查找
1 数据结构基础
本章所需相关基础知识:
- Python基础学习笔记(二)—— 数据类型及操作
- Python基础学习笔记(六)—— 面向对象编程(1)
1.1 数组
1. 数组的基本结构
数组是最常见的一种数据结构,其由有限个类型相同的变量按照一定的顺序组合构成,在Python中常常利用列表(list)来表示数组。Python定义数组的时候与C/C++中定义数组时的区别在于定义时无序指定长度,可以动态增长,不断向后追加元素,一般不会出现数组溢出的状况,为编程者带来了极大的自由度。
# 一维数组
arr1 = [1, 2, 3, 4]
print(arr1) # [1, 2, 3, 4]
print(arr1[0]) # 1# 二维数组
arr2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
print(arr2) # [[1, 2, 3, 4], [5, 6, 7, 8]]
print(arr2[0][3]) # 4
# 一般通过如下方式定义一个二维数组
arr3 = [[i for i in range(4)] for j in range(3)]
print(arr3) # [[0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3]]
2. 数组的基本操作
# 定义
arr = [1, 2, 3, 4, 5, 1]# 增加
# arr.append(6)
# print(arr) # [1, 2, 3, 4, 5, 1, 6]# 删除(利用pop(),remove(),del()方法删除元素)
# 1. pop([索引]) 删除指定索引对应的元素,默认删除数组最后一个元素,并返回该值
# arr.pop()
# arr.pop(1)
# 2. remove(元素值) 删除数组里某个值的第一个匹配项
# arr.remove(1)
# 3. del() 按照索引删除元素
# del(arr[2])
# del arr[2]# 插入
# insert(插入的索引位置,插入的元素)
# arr.insert(0, 100)# 查找
# 1. 想确定数组中是否含有某一个元素
# if 200 in arr:
# print("True")
# 2. 想确定某个元素的索引,index(元素值) 查找数组中该元素第一次出现的索引
# arr.index(1)# 修改
# 通过索引直接访问重新赋值即可
# arr[0] = 9# 反转
# reverse()方法反转列表,直接对数组进行操作,没有产生额外的空间
# arr.reverse()# 排序
# sort(key=None,reverse=False)默认升序,修改reverse=True则为降序
# arr.sort()
# arr.sort(reverse=True)# 清空
# 对数组进行清空,输出[]
# arr.clear()# 截取
# 按步长截取,顾头不顾尾
# 数组名[起始索引(不写则默认包含数组开始的所有元素),终止索引(不写则默认包含到数组结束的所有元素),步长(默认为1)]
# print(arr[::2]) # [1, 3, 5]
# print(arr[::-1]) # [1, 5, 4, 3, 2, 1]
# print(arr[:-1]) # [1, 2, 3, 4, 5]
1.2 链表
1. 链表的基本结构
链表主要包括单向链表和双向链表,这是一种无须在内存中顺序存储即可保持数据之间逻辑关系的数据结构。
链表是由一个个节点(Node)连接而成的,每个节点都是包含数据域(Data)和指针域(Next)的基本单元。其基本元素如下:
- 链表节点:每个节点分为两部分,即数据域和指针域
- 数据域:数据域内一般存储的是整型、浮点型等数字类型
- 指针域:指针域内一般存储的是下一个节点所在的内存空间地址
- 头节点:指向链表的第一个节点
- 尾节点:指向链表的最后一个节点
- None:链表的最后一个节点的指针域,为空
单链表
单链表的每个节点的指针域只指向下一个节点,整个链表是无环的
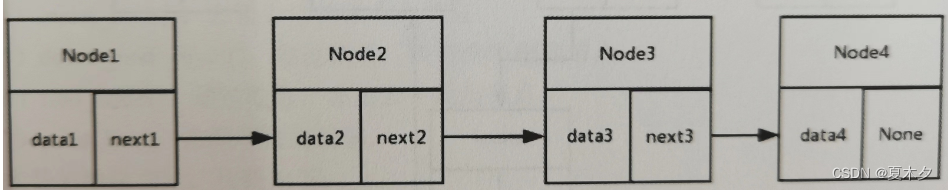
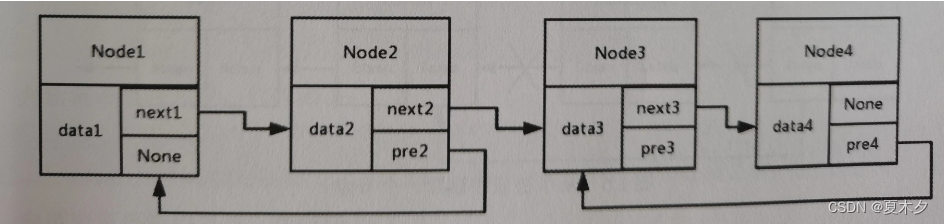
双向链表
单向循环链表
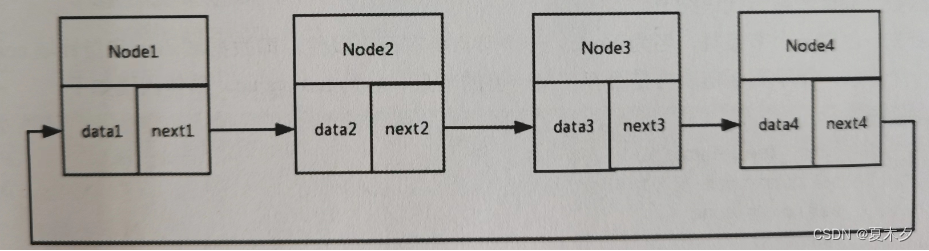
相比于数组,在链表中执行插入、删除等操作可以使得操作效率大大提高。
以单链表为例,在数组内如想要删除或者插入元素到某一位置,该位置之后的所有元素都需要象前或者向后移动,这样一来,时间复杂度就与数组的长度有关,为O(n);但是在单链表中,仅仅需要通过改变所要删除或者插入位置前后节点的指针域即可,时间复杂度为O(1)。
2. 单链表的实现与基本操作
# 链表结点
class Node(object):def __init__(self, item):self.item = itemself.next = None# 单链表
class SingleLink(object):# 选择该初始化方法,调用时使用 SingleLink(node)def __init__(self, node=None):self.head = node# 选择该初始化方法,调用时就不能使用上面的 SingleLink(node),初始化只能通过append添加节点# def __init__(self):# self.head = None# 判断单链表是否为空def is_empty(self):if self.head is None:return Trueelse:return False# 获取链表长度def length(self):cur = self.headcount = 0while cur is not None:cur = cur.nextcount += 1return count# 遍历链表def travel(self):cur = self.headwhile cur is not None:print(cur.item)cur = cur.next# 链表头部增加结点def add(self, item):node = SingNode(item)node.next = self.headself.head = node# 链表尾部增加结点"""注意:如果链表为空链表,cur是没有next的,只需self.head=node"""def append(self, item):node = SingNode(item)if self.is_empty():self.head = nodeelse:cur = self.headwhile cur.next is not None:cur = cur.nextcur.next = node# 链表指定位置增加结点def insert(self, pos, item):if pos == 0:self.add(item)elif pos >= self.length():self.append(item)else:node = SingNode(item)cur = self.headcount = 0while count < pos - 1:cur = cur.nextcount += 1node.next = cur.nextcur.next = node# 删除结点def remove(self, item):cur = self.headpre = Nonewhile cur is not None:# 找到了要删除的元素if cur.item == item:# 如果要删除的位置在头部if cur == self.head:self.head = cur.next# 要删除的位置不在头部else:pre.next = cur.nextreturn # 删除元素后及时退出循环# 没有找到要删除的元素else:pre = curcur = cur.next# 查找结点def search(self, item):cur = self.headwhile cur is not None:if cur.item == item:return Truecur = cur.nextreturn False
1.3 队列
1. 队列的基本结构
队列最基本的特点就是先进先出,在队列尾部加入新元素,在队列头部删除元素,分为双端队列和一般的单端队列。
队列的作用:对于任务处理类的系统,即先把用户发起的任务请求接收过来存到队列中,然后后端开启多个应用程序从队列中取任务进行处理,队列起到了 缓冲压力 的作用
2. 队列的实现与基本操作
利用列表来简单地模拟队列
class Queue(object):def __init__(self):self.items = []# 入队def enqueue(self, item):self.items.append(item)# 出队def dequeue(self):self.items.pop(0)# 队列的大小def size(self):return len(self.items)# 判断队列是否为空def is_empty(self):return self.items == []
对于队列这种数据结构,Python的 queue 类模块中提供了一种先进先出的队列模型 Queue,可以限制队列的长度也可以不限制,在创建队列时利用 Queue(maxsize=0),maxsize小于等于0表示不限制,否则表示限制。
我们在编程的过程中也可以通过调用现有类来实现队列
from queue import Queue# 队列的定义
q = Queue(maxsize=0)# put() 在队列尾部添加元素
q.put(1)
q.put(2)
# print(q) # <queue.Queue object at 0x0000020095EE82B0>
# print(q.queue) # deque([1, 2])# get() 在队列头部取出元素,返回队列头部元素
q.get()
print(q.queue) # deque([2])# empty() 判断队列是否为空
print(q.empty()) # False# full(0 判断队列是否达到最大长度限制
print(q.full()) # False# qsize() 队列当前的长度
print(q.qsize()) # 1
3. 双端队列的实现与基本操作
双端队列(deque,全名double-ended queue ), 是一种具有队列和栈的性质的数据结构
双端队列中的元素可以从两端弹出,其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。
class deque(object):def __init__(self):self.items = []# 判断是否为空def is_empty(self):return self.items == []# 队列的大小def size(self):return len(self.items)# 头部添加数据def add_front(self, item):self.items.insert(0, item)# 尾部添加数据def add_rear(self, item):self.items.append(item)# 头部删除数据def remove_front(self):self.items.pop(0)# 尾部删除数据def remove(self):self.items.pop()
1.4 栈
1. 栈的基本结构
栈最突出的特点是先进后出,其插入、删除操作均在栈顶进行。栈一般包括入栈、出栈操作,并且有一个顶指针(top)用于指示栈顶的位置
2. 栈的实现与基本操作
class Stack(object):def __init__(self):self.items = [] # 进栈def push(self, item):self.items.append(item)# 出栈def pop(self):self.items.pop()# 遍历def travel(self):for i in self.items:print(i)# 栈的大小def size(self):return len(self.items)# 栈是否为空def is_empty(self):return self.items == []# return len(self.items) == 0# 返回栈顶元素def peek(self):if self.is_empty():return "栈空"return self.items[self.size()-1]# return self.items[-1]
1.5 二叉树
1. 树
树是一种数据结构,它是由 n 个有限节点组成的一个具有层次关系的集合。
树的基本性质如下:

2. 二叉树的基本结构
二叉树则是每个节点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”。
二叉树的一般性质:
- 二叉树是有序的(左右子树不能颠倒)
- 二叉树的第 k 层上的节点数目最多为 2k−12^{k-1}2k−1
- 深度为 h 的二叉树最多有 2h−12^h-12h−1 个节点
- 设非空二叉树中度为0、1 和 2 的结点个数分别为n0n_0n0 、n1n_1n1 和 n2n_2n2,则 n0=n2+1n_0 = n_2+1n0=n2+1
(叶子结点比二分支结点多一个)
其他常见的二叉树:
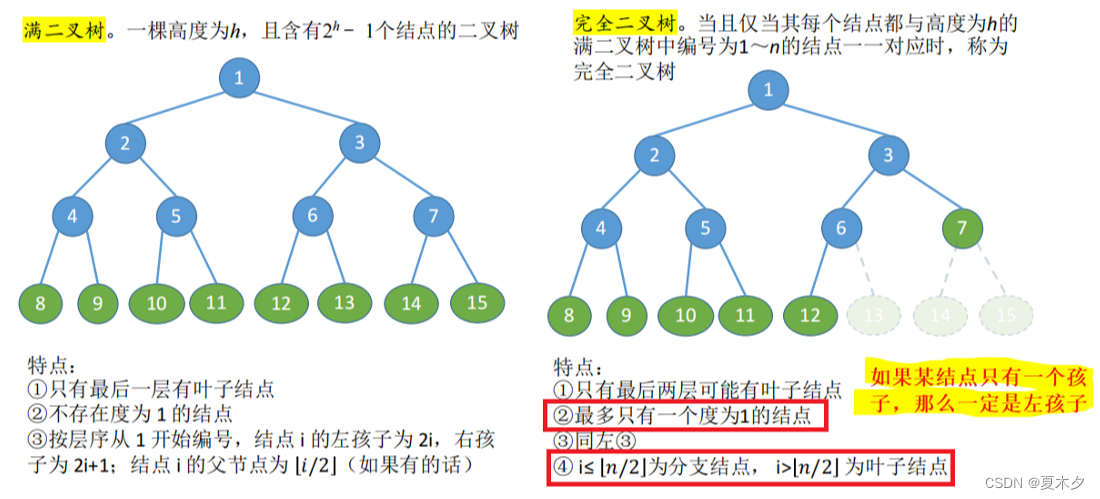

二叉树通常以链式存储
3. 二叉树的实现与基本操作
# 定义节点类
class Node(object):def __init__(self, item):self.item = itemself.lchild = Noneself.rchild = None# 定义二叉树
class BinaryTree(object):def __init__(self, node=None):self.root = node"""思路分析:首先在队列中插入根节点,取出该节点,再判断该节点的左右子树是否为空,左子节点不空,将其入队,右子节点不空,将其入队,再分别判断左右节点的左右子节点是否为空,循环往复,直到发现某个子节点为空,即把新节点添加进来"""# 添加节点def add(self, item):node = Node(item)# 二叉树为空if self.root is None:self.root = nodereturn# 二叉树不空queue = []queue.append(self.root)while True:# 从队头取出数据node1 = queue.pop(0)# 判断左节点是否为空if node1.lchild is None:node1.lchild = nodereturnelse:queue.append(node1.lchild)# 判断右节点是否为空if node1.rchild is None:node1.rchild = nodereturnelse:queue.append(node1.rchild)# 广度优先遍历,也叫层次遍历def breadth(self):if self.root is None:returnqueue = []queue.append(self.root)while len(queue) > 0:# 取出数据node = queue.pop(0)print(node.item, end=" ")# 判断左右子节点是否为空if node.lchild is not None:queue.append(node.lchild)if node.rchild is not None:queue.append(node.rchild)# 深度优先遍历# 先序遍历(根左右)def preorder_travel(self, root):if root is not None:print(root.item, end="")self.preorder_travel(root.lchild)self.preorder_travel(root.rchild)# 中序遍历(左根右)def inorder_travel(self, root):if root is not None:self.inorder_travel(root.lchild)print(root.item, end="")self.inorder_travel(root.rchild)# 后序遍历(左右根)def postorder_travel(self, root):if root is not None:self.postorder_travel(root.lchild)self.postorder_travel(root.rchild)print(root.item, end="")
注意:
- 广度优先遍历基于队列
- 深度优先遍历基于栈
试试 LeetCode 相关题目吧
- 102. 二叉树的层序遍历
- 144.二叉树的前序遍历
- 94. 二叉树的中序遍历
- 145. 二叉树的后序遍历
4. 由遍历结果反推二叉树结构
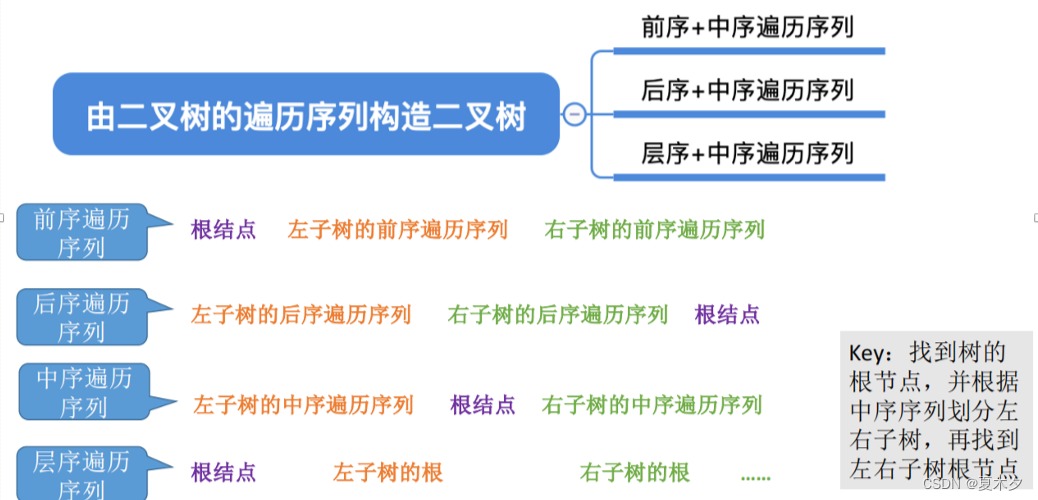
2 排序算法
算法的稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变则称这种排序算法是稳定的,否则称为不稳定的
- 不稳定的排序算法:选择排序、快速排序、希尔排序、堆排序
- 稳定的排序算法:冒泡排序、插入排序、归并排序、基数排序
2.1 冒泡排序
对要进行排序的数据中相邻的数据进行两两比较,将较大的数据放在后面,依次对所有的数据进行操作,直至所有数据按要求完成排序
如果有n个数据进行排序,总共需要比较 n-1 次
每一次比较完毕,下一次的比较就会少一个数据参与
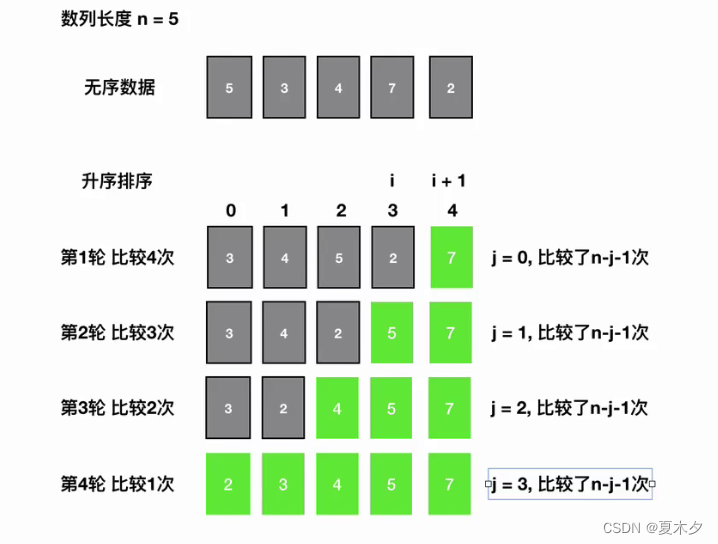
def bubble_sort(lis):n = len(lis)# 控制比较的轮数for j in range(n - 1):count = 0# 控制每一轮的比较次数# -1是为了让数组不要越界# -j是每一轮结束之后, 我们就会少比一个数字for i in range(n - 1 - j):if lis[i] > lis[i + 1]:lis[i], lis[i + 1] = lis[i + 1], lis[i]count += 1# 算法优化# 如果遍历一遍发现没有数字交换,退出循环,说明数列是有序的if count == 0:breakif __name__ == "__main__":lis = [2, 7, 3, 6, 9, 4]bubble_sort(lis)print(lis)
总结:
- 冒泡排序是稳定的
- 最坏时间复杂度为O(n2)O(n^2)O(n2)
- 最优时间复杂度为O(n)O(n)O(n),遍历一遍发现没有任何元素发生了位置交换终止排序
2.2 快速排序
快速排序算法中,每一次递归时以第一个数为基准数 ,找到数组中所有比基准数小的。再找到所有比基准数大的。小的全部放左边,大的全部放右边,确定基准数的正确位置。
def quick_sort(lis, left, right):# 递归的结束条件:left > rightif left > right:return# 存储临时变量,left0始终为0,right0始终为len(lis)-1left0 = leftright0 = right# 基准值base = lis[left0]# left != rightwhile left != right:# 从右边开始找寻小于mid的值while lis[right] >= base and left < right:right -= 1# 从左边开始找寻大于mid的值while lis[left] <= base and left < right:left += 1# 交换两个数的值lis[left], lis[right] = lis[right], lis[left]# left=right# 基准数归位lis[left0], lis[left] = lis[left], lis[left0]# 递归操作quick_sort(lis, left0, left - 1)quick_sort(lis, left + 1, right0) # quick_sort(lis, left + 1, right0)if __name__ == '__main__':lis = [1, 2, 100, 50, 1000, 0, 10, 1]quick_sort(lis, 0, len(lis) - 1)print(lis)
总结:
- 快速排序算法不稳定
- 最好的时间复杂度:O(nlog2n)O(nlog_2n)O(nlog2n),初始序列大小均匀,每一次选择的基准值将待排序的序列划分为均匀的两部分,递归深度最小,算法效率最高
- 最坏的时间复杂度:O(n2)O(n^2)O(n2),初始序列有序或逆序,每次选择的基准值都是靠边的元素,递归深度最大,算法效率最低
2.3 (简单)选择排序
第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾,以此类推,直到全部待排序的数据元素的个数为零。
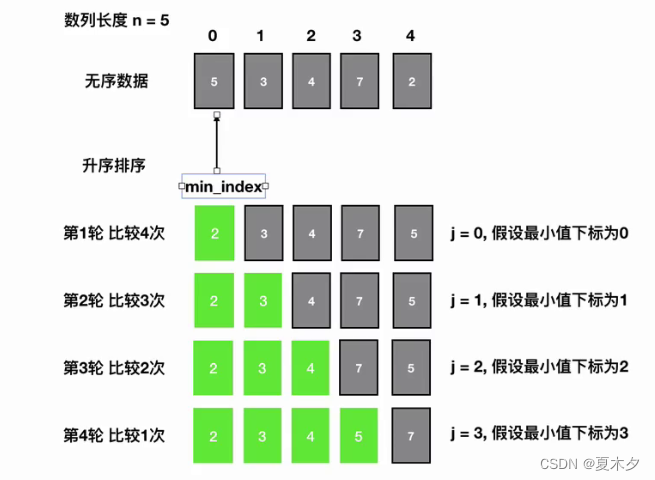
def select_sort(lis):n = len(lis)# 控制比较的轮数for j in range(n - 1):# 假定最小值的下标min_index = j# 控制每一轮的比较次数for i in range(j + 1, n):# 进行比较获得最小值下标if lis[min_index] > lis[i]:min_index = i# 如果假定的最小值下标发生了变化,那么就进行交换if min_index != j:lis[min_index], lis[j] = lis[j], lis[min_index]if __name__ == "__main__":lis = [2, 7, 3, 6, 9, 4]select_sort(lis)print(lis)
总结:
- 选择排序是不稳定的
- 最坏时间复杂度为O(n^2)
- 最优时间复杂度为O(n^2)
2.4 堆排序
堆排序是不稳定的
2.5 (直接)插入排序
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序
插入算法把要排序的数组分成两部分:
- 第一部分是有序的数字(这里可以默认数组第一个数字为有序的第一部分)
- 第二部分为无序的数字(这里除了第一个数字以外剩余的数字可以认为是无序的第二部分)
def insert_sort(lis):n = len(lis)# 控制比较的轮数,即无序数据的个数,一个数肯定是有序的,不用比较for j in range(1, n):# 控制每一轮的比较次数# i取值范围[j,j-1,j-2,j-3,,,1]# 取出无序部分的首个,在有序部分从后向前比较,插入到合适的位置for i in range(j, 0, -1):# 找到合适的位置安放无序数据if lis[i] < lis[i - 1]:lis[i], lis[i - 1] = lis[i - 1], lis[i]else:breakif __name__ == "__main__":lis = [2, 7, 3, 6, 9, 4]insert_sort(lis)print(lis)
总结:
- 直接插入排序是稳定的
- 最坏时间复杂度为O(n^2),本身倒序
- 最优时间复杂度为O(n),本身有序,每一轮只需比较一次
3 查找
3.1 二分查找
二分查找的适用前提:必须有序
非递归方法
def binary_search(lis, num):left = 0right = len(arr) - 1while left <= right:mid = (left + right) // 2if num > lis[mid]:left = mid + 1elif num < lis[mid]:right = mid - 1else: # num == arr[mid]return midreturn -1if __name__ == "__main__":lis = [1, 3, 5, 7, 9, 10]print(binary_search(lis, 5)) # 2print(binary_search(lis, 8)) # -1
递归方法
相关文章:

Python基础学习笔记 —— 数据结构与算法
数据结构与算法1 数据结构基础1.1 数组1.2 链表1.3 队列1.4 栈1.5 二叉树2 排序算法2.1 冒泡排序2.2 快速排序2.3 (简单)选择排序2.4 堆排序2.5 (直接)插入排序3 查找3.1 二分查找1 数据结构基础 本章所需相关基础知识:…...

笔记本连接wifi,浏览器访问页面,显示访问被拒绝
打开chrome、edge浏览器访问第1个第2个页面正常,后面再打开页面显示异常。 但手机连接正常,笔记本连接异常,起初完全没有怀疑是wifi问题 以为用了vpn软件问题,认为中了病毒。杀毒,并没有中毒。 1、关闭vpn代理&#…...

36个物联网专业毕业论文选题推荐
物联网技术在智能家居系统中的应用研究物联网在智慧城市建设中的作用物联网在工业4.0中的实现与发展 物联网与智能物流系统的结合物联网与医疗健康领域的融合研究物联网与环境监测系统的集成物联网与农业生产的结合研究物联网技术对汽车行业的影响与发展物联网在智能安防领域的…...
Pytorch复习笔记--torch.nn.functional.interpolate()和cv2.resize()的使用与比较
1--前言 博主在处理图片尺度问题时,习惯使用 cv2.resize() 函数;但当图片数据需用显卡加速运算时,数据需要在 GPU 和 CPU 之间不断迁移,导致程序运行效率降低; Pytorch 提供了一个类似于 cv2.resize() 的采样函数&…...

ASP.NET Core MVC 项目 AOP之ActionFilterAttribute
目录 一:说明 二:实现ActionFilterAttribute父类 一:说明 ActionFilterAttribute比前两者简单方便,易于扩展,不易产生代码冗余。 ActionFilterAttribute过滤器执行顺序: 1:执行控制器中的构造函数,实例化控制器 2:执行ActionFilterAttribute.OnActionExecutionA…...
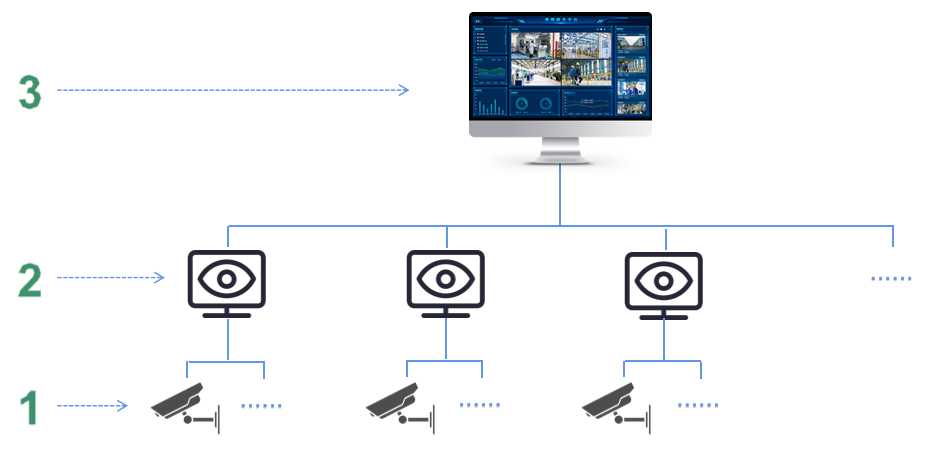
浅析EasyCVR安防视频能力在智慧小区建设场景中的应用及意义
一、行业需求 城市的发展创造了大量工作机会,人口的聚集也推动了居民住宅建设率的增长。人民生活旨在安居乐业,能否住得“踏实”是很多劳动工作者最关心的问题。但目前随着住宅小区规模的不断扩大、人口逐渐密集,在保证居住环境舒适整洁的同…...

Python的深、浅拷贝到底是怎么回事?一篇解决问题
嗨害大家好鸭!我是小熊猫~ 一、赋值 Python中, 对象的赋值都是进行对象引用(内存地址)传递, 赋值(), 就是创建了对象的一个新的引用, 修改其中任意一个变量都会影响到另一个 will …...

TCP协议十大特性
日升时奋斗,日落时自省 目录 1、确认应答 1.1、序号编辑 2、超时重传 3、连接管理 3.1、三次握手 3.2、四次挥手 4、滑动窗口 5、流量控制 6、拥塞控制 7、延时应答 8、捎带应答 9、面向字节流 10、异常情况 TCP协议: 特点:有…...

2.14作业【GPIIO控制LED】
设备树 myleds{ myled1 <&gpioe 10 0>; myled2 <&gpiof 10 0>; myled3 <&gpioe 8 0>; }; 驱动代码 #include<linux/init.h> #include<linux/module.h> #include<linux/of.h&…...

5min搞定linux环境Jenkins的安装
5min搞定linux环境Jenkins的安装 安装Jenkinsstep1: 使用wget 命令下载Jenkinsstep2、创建Jenkins日志目录并运行jekinsstep3、访问jenkins并解锁jenkins,安装插件以及创建管理员用户step4、到此,就完成了Finish、以上步骤中遇到的问题1、 jenkins启动不了2、jenkins无法访问…...
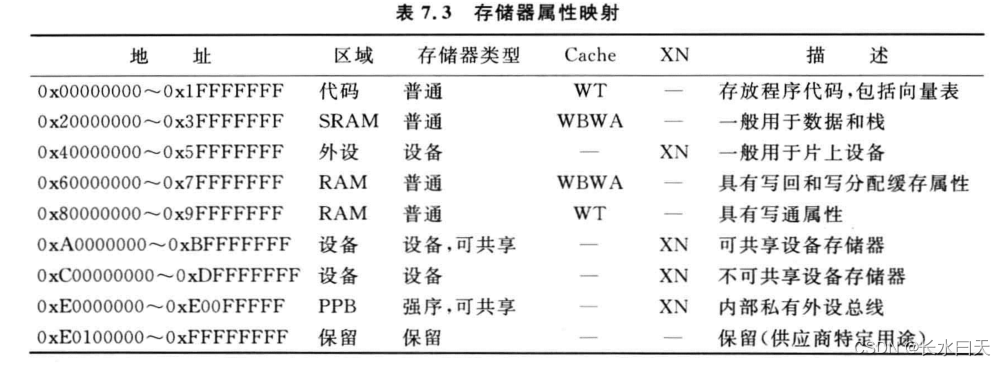
Cortex-M0存储器系统
目录1.概述2.存储器映射3.程序存储器、Boot Loader和存储器重映射4.数据存储器5.支持小端和大端数据类型数据对齐访问非法地址多寄存器加载和存储指令的使用6.存储器属性1.概述 Cortex-M0处理器具有32位系统总线接口,以及32位地址线(4GB的地址空间&…...
软件测试——测试用例之场景法
一、场景法的应用场合 场景法主要用于测试软件的业务流程和业务逻辑。场景法是基于软件业务的测试方法。在场景法中测试人员把自己当成最终用户,尽可能真实的模拟用户在使用此软件的操作情景: 重点模拟两类操作: 1)模拟用户正确…...

英文写作中的常用的衔接词
1. 增补 (Addition) in addition, furthermore, again, also, besides, moreover, whats more, similarly, next, finally 2.比较(Comparision) in the same way, similarly, equally, in comparison, just as 3. 对照 (Contrast) in contrast, on …...

新库上线 | CnOpenData中国地方政府债券信息数据
中国地方政府债券信息数据 一、数据简介 地方政府债券 指某一国家中有财政收入的地方政府地方公共机构发行的债券。地方政府债券一般用于交通、通讯、住宅、教育、医院和污水处理系统等地方性公共设施的建设。地方政府债券一般也是以当地政府的税收能力作为还本付息的担保。地…...

Python 条件语句
Python条件语句是通过一条或多条语句的执行结果(True或者False)来决定执行的代码块。 可以通过下图来简单了解条件语句的执行过程: Python程序语言指定任何非0和非空(null)值为true,0 或者 null为false。 Python 编…...
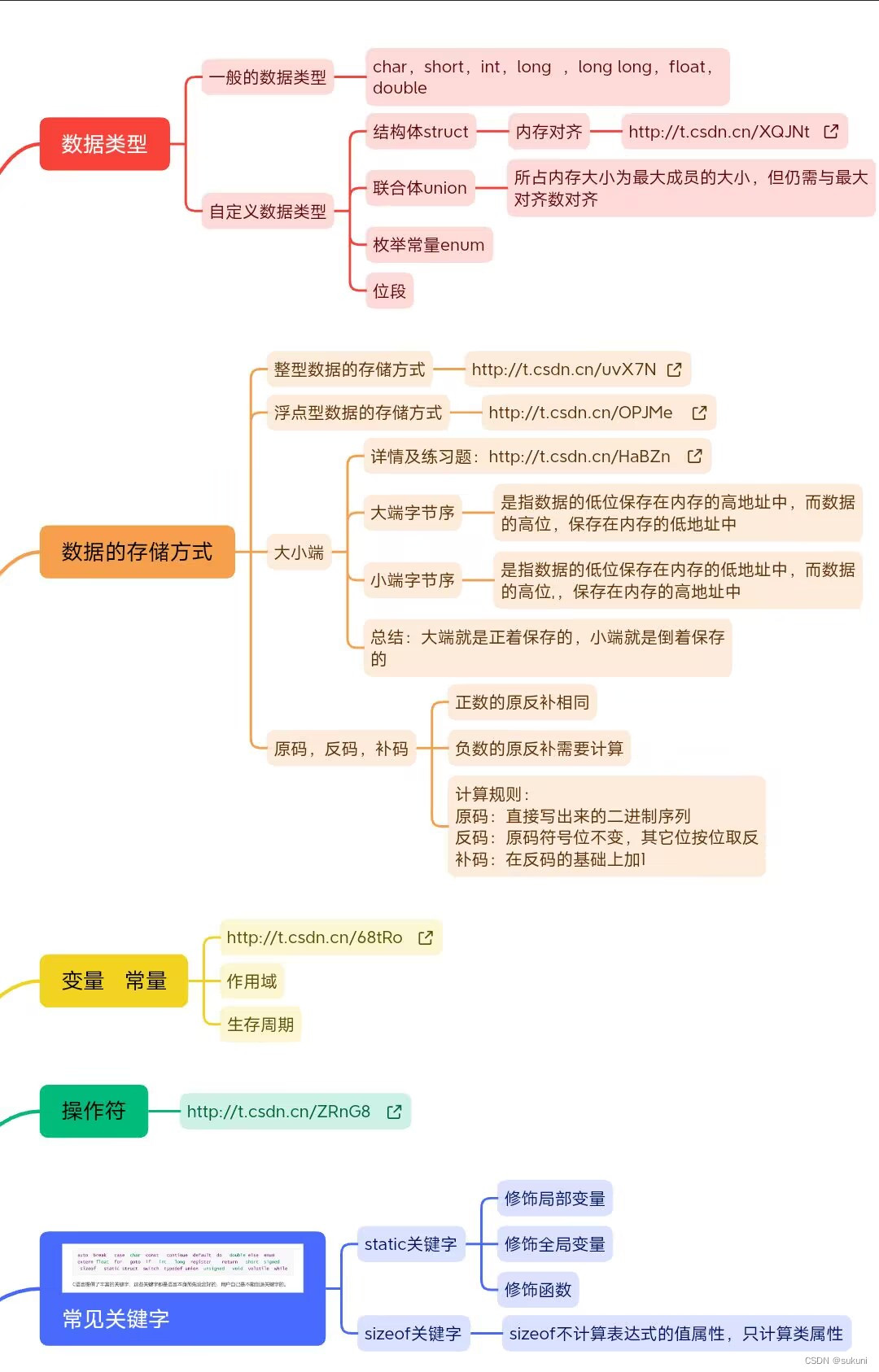
C语言思维导图大总结 可用于期末考试 C语言期末考试题库
目录 一.C语言思维导图 二.C语言期末考试题库 一.C语言思维导图 导出的图可能有点糊,或者查看链接:https://share.weiyun.com/uhf1y2mp 其实原图是彩色的不知道为什么导出时颜色就没了 部分原图: 也可私信我要全图哦。 图里的链接可能点不…...

从零实现深度学习框架——再探多层双向RNN的实现
来源:投稿 作者:175 编辑:学姐 往期内容: 从零实现深度学习框架1:RNN从理论到实战(理论篇) 从零实现深度学习框架2:RNN从理论到实战(实战篇) 从零实现深度…...
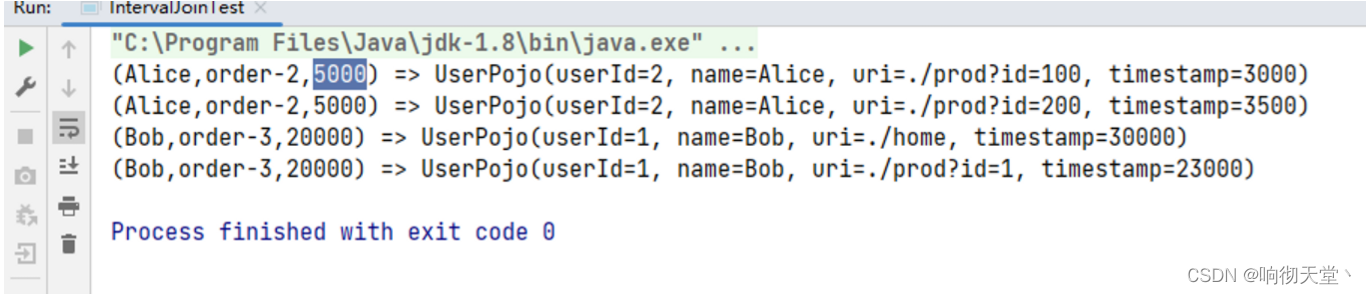
Flink 连接流详解
连接流 1 Union 最简单的合流操作,就是直接将多条流合在一起,叫作流的“联合”(union)。联合操作要求必须流中的数据类型必须相同,合并之后的新流会包括所有流中的元素,数据类型不变。这种合流方式非常简…...

分享112个HTML电子商务模板,总有一款适合您
分享112个HTML电子商务模板,总有一款适合您 112个HTML电子商务模板下载链接:https://pan.baidu.com/s/13wf9C9NtaJz67ZqwQyo74w?pwdzt4a 提取码:zt4a Python采集代码下载链接:采集代码.zip - 蓝奏云 有机蔬菜水果食品商城网…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(八)
马上就又到了程序员们躁动不安,蠢蠢欲动的季节~这不,金三银四已然到了家门口,元宵节一过后台就有不少人问我:现在外边大厂面试都问啥想去大厂又怕面试挂面试应该怎么准备测试开发前景如何面试,一个程序员成长之路永恒绕…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
