【高数+复变函数】傅里叶积分
文章目录
- 【高数+复变函数】傅里叶积分
- 2. 傅里叶积分
- 2.1 复数形式积分公式
- 2.2 三角形式
上一节: 【高数+复变函数】傅里叶级数
【高数+复变函数】傅里叶积分
2. 傅里叶积分
在上一节中,我们知道了傅里叶级数的基本知识,其中,周期为 2 l 2l 2l的函数的傅里叶展开为:
f ( x ) = a 0 2 + ∑ n = 1 x ( a n cos n π x l + b n sin n π x l ) f(x)=\frac{a_0}{2}+\sum\limits_{n=1}^{x}\left(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac{n\pi x}{l}\right) f(x)=2a0+n=1∑x(ancoslnπx+bnsinlnπx)令 w = π l w=\frac{\pi}{l} w=lπ,上式就变成了:
f ( x ) = a 0 2 + ∑ n = 1 x ( a n cos n w x + b n sin cos n w x ) f(x)=\frac{a_0}{2}+\sum\limits_{n=1}^{x}\left(a_n\cos{nw x}+b_n\sin\cos{nw x}\right) f(x)=2a0+n=1∑x(ancosnwx+bnsincosnwx)在复变函数中,我们常使用 T T T为周期,也就是 T = 2 l T=2l T=2l,所以傅里叶级数展开式也就变成了:
f T ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n ω t + b n sin n ω t ) f_T(t)=\frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos n\omega t+b_n\sin n\omega t) fT(t)=2a0+n=1∑∞(ancosnωt+bnsinnωt)其中:
ω = 2 π T . a 0 = 2 T ∫ − T 2 T 2 f T ( t ) d t , a n = 2 T ∫ − T 2 T 2 f T ( t ) c o s n w t d t ( n = 1 , 2 , 3 , ⋯ ) , b n = 2 T ∫ − T 2 T 2 f T ( t ) s i n n w t d t ( n = 1 , 2 , 3 , ⋯ ) . \begin{array}{l}\omega=\frac{2\pi}{T}.\\ a_{0}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_{T}(t)\mathrm{d}t,\\ a_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_{T}(t)\mathrm{cos}nwtdt\quad(n=1,2,3,\cdots),\\ b_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_{T}(t)\mathrm{sin}nwtdt\quad(n=1,2,3,\cdots).\end{array} ω=T2π.a0=T2∫−2T2TfT(t)dt,an=T2∫−2T2TfT(t)cosnwtdt(n=1,2,3,⋯),bn=T2∫−2T2TfT(t)sinnwtdt(n=1,2,3,⋯).
2.1 复数形式积分公式
之后我们把他化成复数形式,利用:
cos φ = e j φ + e − j φ 2 , sin φ = e j φ − e − j φ 2 j = − j e j φ − e − j φ 2 \cos\varphi=\frac{\mathrm{e}^{j\varphi}+\mathrm{e}^{-j\varphi}}{2},\sin\varphi=\frac{\mathrm e^{j\varphi}-\mathrm e^{-j\varphi}}{2\mathrm j}=-j\frac{\mathrm e^{j\varphi}-\mathrm e^{-j\varphi}}{2} cosφ=2ejφ+e−jφ,sinφ=2jejφ−e−jφ=−j2ejφ−e−jφ
代入可得
f T ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n − j b n 2 e j n ω t + a n + j b n 2 e − j n ω t ) f_T(t)=\frac{a_0}{2}+\sum\limits_{n=1}^\infty\left(\frac{a_n-jb_n}{2}\mathrm{e}^{jn\omega t}+\frac{a_n+jb_n}{2}\mathrm{e}^{-jn\omega t}\right) fT(t)=2a0+n=1∑∞(2an−jbnejnωt+2an+jbne−jnωt)
之后进行替换:
c n = 1 T ∫ − T 2 T 2 f T ( t ) e − j n ω t d t ( n = 0 , ± 1 , ± 2 , ⋯ ) ω n = n ω ( n = 0 , ± 1 , ± 2 , ⋯ ) c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)e^{-j n\omega t}\mathrm{d}t\quad(n=0,\pm1,\pm2,\cdots)\\\omega_n=n\omega(n=0,\pm1,\pm2,\cdots) cn=T1∫−2T2TfT(t)e−jnωtdt(n=0,±1,±2,⋯)ωn=nω(n=0,±1,±2,⋯)
即可得Fourier级数的复指数形式:
f T ( t ) = ∑ n = − ∞ + ∞ c n e j ω n t = 1 T ∑ n = − ∞ + ∞ [ ∫ − T 2 T 2 f T ( τ ) e − j ω n τ d τ ] e j ω n t f_T(t)=\sum\limits_{n=-\infty}^{+\infty}c_n\mathbf{e}^{j\omega_nt}=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\Big[\int_{-\frac{T}{2}}^{\frac{T}{2}}f_{T}(\tau)\mathrm{e}^{-j\omega_{n}\tau}\mathrm{d}\tau\Big]\mathrm{e}^{j\omega_{n}t} fT(t)=n=−∞∑+∞cnejωnt=T1n=−∞∑+∞[∫−2T2TfT(τ)e−jωnτdτ]ejωnt
现在我们再来考虑非周期函数能否用Fourier积分来表示:
易知:
lim T → ∞ f T ( t ) = f ( t ) \lim\limits_{T\to\infty}f_{T}(\begin{matrix}t\end{matrix})=f(\begin{matrix}t\end{matrix}) T→∞limfT(t)=f(t)
所以我们可以通过给复指数形式求极限得到 f ( t ) f(t) f(t),求极限的过程中也可消去连加号(过程省略),最终Fourier积分公式为:
f ( t ) = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( τ ) e − j ω τ d τ ] e j ω t d ω . f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\left[\int_{-\infty}^{+\infty}f(\tau)\mathrm e^{-j\omega\tau}\mathrm d\tau\right]\mathrm e^{j\omega t}\mathrm d\omega. f(t)=2π1∫−∞+∞[∫−∞+∞f(τ)e−jωτdτ]ejωtdω.
至于一个非周期函数 f ( t ) f(t) f(t)在什么条件下,可以用Fourier积分公式来表示,有下列定理:

2.2 三角形式

f ( t ) = 1 π ∫ 0 + ∞ [ ∫ − ∞ + ∞ f ( τ ) cos ω ( t − τ ) d τ ] d ω (1.6) f(t)=\frac{1}{\pi}\int_{0}^{+\infty}[\int_{-\infty}^{+ \infty}f(\tau)\cos\omega(t-\tau)\mathrm{d}\tau]\mathrm{d}\omega \tag{1.6} f(t)=π1∫0+∞[∫−∞+∞f(τ)cosω(t−τ)dτ]dω(1.6)
这便是 f ( t ) f(t) f(t)的Fourier积分公式的三角形式。
(1.6)式还可写为:
f ( t ) = 1 π ∫ 0 ∞ [ ∫ − ∞ + ∞ f ( τ ) ( cos ω t cos ω τ + sin ω t sin ω τ ) d τ ] d ω . f(t)=\frac{1}{\pi}\int_0^{\infty}\left[\int_{-\infty}^{+\infty}f(\tau)\left(\cos\omega t\cos\omega\tau+\sin\omega t\sin\omega\tau\right)\mathrm{d}\tau\right]\mathrm{d}\omega. f(t)=π1∫0∞[∫−∞+∞f(τ)(cosωtcosωτ+sinωtsinωτ)dτ]dω.
当 f ( t ) f(t) f(t)是奇函数时:
f ( t ) = 2 π ∫ 0 + ∞ [ ∫ 0 + ∞ f ( τ ) sin ω τ d τ ] sin ω t d ω . f(t)=\frac{2}{\pi}\int_0^{+\infty}\Big[\int_0^{+\infty}f(\tau)\sin\omega\tau\mathrm d\tau\Big]\sin\omega t\mathrm d\omega. f(t)=π2∫0+∞[∫0+∞f(τ)sinωτdτ]sinωtdω.
当 f ( t ) f(t) f(t)是偶函数时:
f ( t ) = 2 π ∫ 0 + ∞ [ ∫ 0 + ∞ f ( τ ) cos ω τ d τ ] cos ω t d ω . f(t)=\frac{2}{\pi}\int_{0}^{+\infty}\left[\int_{0}^{+\infty}f(\tau)\cos\omega\tau\text{d}\tau\right]\cos\omega t\text{d}\omega. f(t)=π2∫0+∞[∫0+∞f(τ)cosωτdτ]cosωtdω.
它们分别称为 Fourier 正弦积分公式和 Fourier 余弦积分公式。
特别,如果 f ( t ) f(t) f(t)仅在 ( 0 , + ∞ ) (0,+\infty) (0,+∞)上有定义且满足 Fourier 积分存在定理的条件,我们可以采用类似于Fourier 级数中的奇延拓或偶延拓的方法,得到 f ( t ) f(t) f(t)相应的 Fourier 正弦积分展开式或 Fourier 余弦积分展开式
我们可以利用 f ( t ) f(t) f(t)的Fourier积分表达式推证一些反常积分的结果:
例: 求函数 f ( t ) = { 1 , ∣ t ∣ ≤ 1 0 , 其他 f(t)=\left\{\begin{array}{l l}{1,}&{\left|t\right|\leq1}\\ {0,}&{其他}\\ \end{array}\right. f(t)={1,0,∣t∣≤1其他的Fourier积分表达式
根据余弦积分公式,可得出:
2 π ∫ 0 + ∞ sin ω cos ω t ω d ω = { f ( t ) , t ≠ ± 1 , 1 2 , t = ± 1 , \frac{2}{\pi}\int_0^{+\infty}\frac{\sin\omega\cos\omega t}{\omega}\mathrm{d}\omega=\begin{cases}f(t),\quad t\ne\pm1,\\[2ex]\frac{1}{2},\quad t=\pm1,\end{cases} π2∫0+∞ωsinωcosωtdω=⎩ ⎨ ⎧f(t),t=±1,21,t=±1,
等价于:
∫ 0 + ∞ sin ω cos ω t ω d ω = { π 2 , ∣ t ∣ < 1 , π 4 , ∣ t ∣ = 1 , 0 , ∣ t ∣ > 1. \int_{0}^{+\infty}\frac{\sin\omega\cos\omega t}{\omega}\mathrm{d}\omega=\begin{cases}\frac{\pi}{2},\quad|t|<1,\\{}\\\frac{\pi}{4},\quad|t|=1,\\{}\\0,\quad|t|>1.\end{cases} ∫0+∞ωsinωcosωtdω=⎩ ⎨ ⎧2π,∣t∣<1,4π,∣t∣=1,0,∣t∣>1.
当t=0时, ∫ 0 + ∞ sin ω ω d ω = π 2 , \int_0^{+\infty}\frac{\sin\omega}{\omega}\mathrm{d}\omega=\frac{\pi}{2}, ∫0+∞ωsinωdω=2π,这就是Dirichlet积分。
相关文章:

【高数+复变函数】傅里叶积分
文章目录 【高数复变函数】傅里叶积分2. 傅里叶积分2.1 复数形式积分公式2.2 三角形式 上一节: 【高数复变函数】傅里叶级数 【高数复变函数】傅里叶积分 2. 傅里叶积分 在上一节中,我们知道了傅里叶级数的基本知识,其中,周期为…...

【Leetcode】241. 为运算表达式设计优先级
241. 为运算表达式设计优先级(中等) 解法一:分治法 对于这道题,加括号其实就是决定运算次序,所以我们可以把加括号转化为,「对于每个运算符号,先执行处理两侧的数学表达式,再处理此…...

torch两个向量除法,对于分母向量中的元素为0是设置为1,避免运算错误
在gpu运行时,如果在进行两个向量除法的时候,对于分母向量中的元素为0是设置为1,避免运算错误。 可以使用torch的division函数以及clamp函数来解决这个问题。具体步骤如下: 使用division函数将分子向量除以分母向量。 使用clamp函…...

NodeJs 最近各版本特性汇总
(预测未来最好的方法就是把它创造出来——尼葛洛庞帝) NodeJs 官方链接 github链接 V8链接 Node.js发布于2009年5月,由Ryan Dahl开发,是一个基于Chrome V8引擎的JavaScript运行环境,使用了一个事件驱动、非阻塞式I/O模…...

python数据分析案例——天猫订单综合分析
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 什么是数据分析 明确目的–获得数据(爬虫,现有,公开的数据)–数据预处理——数据可视化——结论 准备 环境使用: 在开始写我们的代码之前,我们要准备好运行代码的程序 Anacon…...
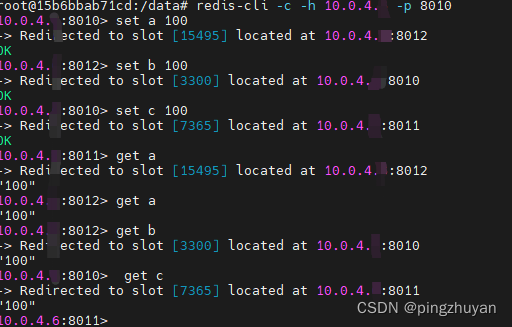
05- redis集群模式搭建(上) (包含云服务器[填坑])
目录 1. 准备环境: 2. 简介: -> 2.1 前言: -> 2.2 Redis集群架构实现了对redis的水平扩容 -> 2.3 redis cluster集群原理 3. 搭建后特别需要注意的问题 ->3.1 [重点]: 如果一个服务出现故障: 是否可以继续提供服务??? ---> 3.1.1 如果集群中故障re…...

【AI】YOLOV1原理详解
AI学习目录汇总 0、前言 YOLOv1~3作者是约瑟夫雷德蒙(Joseph Chet Redmon),他的网站:https://pjreddie.com/ YOLOv1网站:https://pjreddie.com/darknet/yolov1/ YOLOv2网站:https://pjreddie.com/darknet…...
提高APP安全性的必备加固手段——深度解析代码混淆技术
APP 加固方式 Android APP 加固是优化 APK 安全性的一种方法,常见的加固方式有混淆代码、加壳、数据加密、动态加载等。下面介绍一下 Android APP 加固的具体实现方式。 混淆代码: 使用 ProGuard 工具可以对代码进行混淆,使得反编译出来的代…...

想让行车记录仪协助道路病害自动化检测?可以!
针对【RGB3DS道路表观病害信息智慧检测系统】,我们着重介绍过其与道路检测车做集成预装或者处理道路检测车数据的极大便利,其中之一便是可高效输出带有道路检测车桩号标记的病害报表,这是因为道路检测车数据本身具有规范性。 那么如果使用道…...
git上传大大大文件项目好折磨人
本来想把unity项目的源码上传上gitee啊,但是那个项目有1个多G,还是个半成品,要是写完,都不知道行不行 正常的上传 所用到的命令: 1、 git init 初始化,创建本地仓库 2、 git add . 添加到本地仓库 3、 git…...

java常见异常的处理方法
以下是一些常见的异常处理方法: 捕获和处理异常(try-catch): 使用try-catch语句块可以捕获并处理异常。在try块中编写可能抛出异常的代码,然后在catch块中指定异常类型,以便捕获并处理异常。 try {// 可能抛…...

上传图片到阿里云服务器base64 上传
//上传图片到阿里云服务器 function upload_Ali($remoteImage){$imageData $this->n_img_base_64($remoteImage);if ($imageData ! false) {// 初始化 cURL 句柄$ch curl_init();// 设置请求 URL 和一些 cURL 选项curl_setopt($ch, CURLOPT_URL, http://dev.com/index/aja…...

【致敬未来的攻城狮计划】— 连续打卡第二十六天:瑞萨RA Cortex-M 内核RA2E1 RT-Thread BSP 启蒙知识
系列文章目录 由于一些特殊原因: 系列文章链接:(其他系列文章,请点击链接,可以跳转到其他系列文章)或者参考我的专栏“ 瑞萨MCU ”,里面是 瑞萨RA2E1 系列文章。 24.RA2E1的 DMAC——数据传输 …...
)
2023年5月8日-5月14日(方案C,下班UE视频教程为主)
目前,ue视频教程进行到了智 慧 城 市(3.13),mysql(7.1),tf1(4.11),蓝图反射(1.9),moba(1.5)webapp(2.4),mmoarpg(00A_04),fps1_12(0:3…...

「MIAOYUN」:降本增效,赋能传统企业数字化云原生转型 | 36kr 项目精选
作为新经济综合服务平台第一品牌,36氪自2019年落地四川站以来,不断通过新锐、深度的商业报道,陪跑、支持四川的新经济产业。通过挖掘本土优质项目,36氪四川帮助企业链接更多资源,助力企业成长,促进行业发展…...

Python突破JS加密限制,进行逆向解密
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 目录标题 前言开发环境:模块使用:逆向目标逆向过程参数 JS 加密关键代码Python 登录关键代码尾语 💝 开发环境: Python 3.8 Pycharm 模块使用: time >>> 时间模块,属于内置,无…...

【Linux】exec函数族
目录 1、exec函数族的介绍2、exec相关函数 1、exec函数族的介绍 2、exec相关函数 #include <unistd.h> int execl(const char *pathname, const char *arg0, ... /* (char *)0 */ ); /* - path 需要指定的执行的文件的路径或者名称,相对路径or绝对路径- arg …...

OSQP二次规划求解库使用说明
OSQP二次规划求解库使用说明 贺志国 2023.5.10 1. 凸二次规划的一般表达式 m i n 1 2 x T P x q T x s . t . l ≤ A x ≤ u min \quad \frac{1}{2}x^T Px q^Tx \qquad s.t. \quad l \leq Ax \leq u min21xTPxqTxs.t.l≤Ax≤u 其中, P P P称为内核矩阵&#x…...

Elasticsearch(一)
Elasticsearch(一) 初始elasticsearch 什么是elasticsearch elasticsearch是一款非常强大的开源搜索引擎,可以帮助我们从海量数据中快速查找到需要的内容 elasticsearch结合kibana、Logstash、Beats,也就是elastic stack&…...

深入探究Java中的枚举类型:定义、特性和应用
引言: 在Java编程中,枚举类型是一种强大而灵活的工具,用于定义一组具名的常量。它不仅提供了代码可读性和可维护性的优势,还为开发人员提供了一种更安全和结构化的方式来处理固定的常量集合。本文将深入探讨Java中的枚举类型&…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
