PAT A1045 Favorite Color Stripe
1045 Favorite Color Stripe
分数 30
作者 CHEN, Yue
单位 浙江大学
Eva is trying to make her own color stripe out of a given one. She would like to keep only her favorite colors in her favorite order by cutting off those unwanted pieces and sewing the remaining parts together to form her favorite color stripe.
It is said that a normal human eye can distinguish about less than 200 different colors, so Eva's favorite colors are limited. However the original stripe could be very long, and Eva would like to have the remaining favorite stripe with the maximum length. So she needs your help to find her the best result.
Note that the solution might not be unique, but you only have to tell her the maximum length. For example, given a stripe of colors {2 2 4 1 5 5 6 3 1 1 5 6}. If Eva's favorite colors are given in her favorite order as {2 3 1 5 6}, then she has 4 possible best solutions {2 2 1 1 1 5 6}, {2 2 1 5 5 5 6}, {2 2 1 5 5 6 6}, and {2 2 3 1 1 5 6}.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤200) which is the total number of colors involved (and hence the colors are numbered from 1 to N). Then the next line starts with a positive integer M (≤200) followed by M Eva's favorite color numbers given in her favorite order. Finally the third line starts with a positive integer L (≤104) which is the length of the given stripe, followed by L colors on the stripe. All the numbers in a line a separated by a space.
Output Specification:
For each test case, simply print in a line the maximum length of Eva's favorite stripe.
Sample Input:
6
5 2 3 1 5 6
12 2 2 4 1 5 5 6 3 1 1 5 6
Sample Output:
7
* 最长不下降子串的模板;
* 先对喜欢的数字赋一个喜欢度,后选择的数字的喜欢度必定要大于等于前面选择的数字的喜欢度;
* 后面就是最长不下降子串的模板;
*
* 状态设计:dp[i] 表示所有以第i个数结尾的上升子序列的集合的最长长度;
* 状态转移方程:dp[i] = max(dp[j]+1,1) (j=0,1,...,i-1);
* dp[i] = dp[j] + 1 的含义表示i加到j的后面能否形成更长的LIS;
/*** 最长不下降子串的模板;* 先对喜欢的数字赋一个喜欢度,后选择的数字的喜欢度必定要大于等于前面选择的数字的喜欢度;* 后面就是最长不下降子串的模板;* * 状态设计:dp[i] 表示所有以第i个数结尾的上升子序列的集合的最长长度;* 状态转移方程:dp[i] = max(dp[j]+1,1) (j=0,1,...,i-1);* dp[i] = dp[j] + 1 的含义表示i加到j的后面能否形成更长的LIS;
*/#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 1e5+10;
int dp[M], fav[M], ori[M];
int hs[N];int main()
{fill(hs, hs+N, -1); //初始化int n, m, l;cin >> n;cin >> m;for(int i=0; i<m; ++i) {cin >> fav[i];hs[fav[i]] = i;}cin >> l;for(int i=0; i<l; ++i) cin >> ori[i];for(int i=0; i<l; ++i){if(hs[ori[i]] != -1) dp[i] = 1; //只有在喜欢的序列里面才可以选择该数字for(int j=0; j<i; ++j)if(hs[ori[i]] != -1 && hs[ori[i]] >= hs[ori[j]] && dp[j] + 1 > dp[i]){dp[i] = dp[j] + 1;}}cout << *max_element(dp, dp+M);return 0;
}相关文章:

PAT A1045 Favorite Color Stripe
1045 Favorite Color Stripe 分数 30 作者 CHEN, Yue 单位 浙江大学 Eva is trying to make her own color stripe out of a given one. She would like to keep only her favorite colors in her favorite order by cutting off those unwanted pieces and sewing the rem…...
真实业务场景使用-门面模式(外观)设计模式
1.前言 最近接到要修改的业务功能,这个业务增删改查很多功能都需要校验时间,比如: 1.失效时间不能超过自己父表的失效时间, 2.失效时间不能是当前时间 3.失效时间不能早于生效时间 类似这样的不同的判断还有很多,…...

基于多动作深度强化学习的柔性车间调度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

出口亚马逊平衡车CE/UKCA认证注意事项
平衡车UKC认证 CE认证 认证项目:BS EN/EN71-1-2-3 UKCA认证标志与CE认证标志有什么不同? UKCA标记过程基本上遵循与CE标记相同的规则和规定。大多数制造商仍然可以根据测试结果和其他技术文档自行声明他们的产品,但在特定情况下,他们需要从第…...

云原生环境下的安全实践:保护应用程序和数据的关键策略
文章目录 云原生环境下的安全实践:保护应用程序和数据的关键策略一.安全措施和实践1. 身份和访问管理:2. 容器安全:3. 网络安全:4. 日志和监控:5. 持续集成和持续交付(CI/CD)安全:6.…...

vue 改变数据后,数据变化页面不刷新
文章目录 导文文章重点方法一:使用this.$forceUpdate()强制刷新方法二:Vue.set(object, key, value)方法三:this.$nextTick方法四:$set方法 导文 在vue项目中,会遇到修改完数据,但是视图却没有更新的情况 v…...

【Qt编程之Widgets模块】-006:QSortFilterProxyModel代理的使用方法
QSortFilterProxyModel是model的代理,不能单独使用,真正的数据需要另外的一个model提供,它的工鞥呢是对被代理的model(source model)进行排序和过滤。所谓过滤:也就是说按着你输入的内容进行数据的筛选,因为器过滤功能…...

上林赋 汉 司马相如
亡是公听然而笑曰:“楚则失矣,而齐亦未为得也。夫使诸侯纳贡者,非为财币,所以述职也。封疆画界者,非为守御,所以禁淫也。今齐列为东藩,而外私肃慎,捐国逾限,越海而田&…...

7.对象模型
对象模型 信号和槽 信号和槽是一种用于对象之间通信的机制。信号是对象发出的通知,槽是用于接收这些通知的函数。 当对象的状态发生变化时[按钮被点击],它会发出一个信号[clicked()],然后与该对象连接的槽函数将被自动调用。 若某个信号与多…...
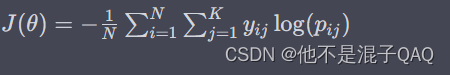
机器学习——基本概念
如何选择合适的模型评估指标?AUC、精准度、召回率、F1值都是什么?如何计算?有什么优缺点? 选择合适的模型评估指标需要结合具体的问题场景,根据不同的需求来选择不同的指标。以下是几个常用的评估指标: AUC…...

Qt---感觉挺重要的部分
目录 一、讲述Qt信号槽机制与优势与不足 二、Qt信号和槽的本质是什么 三、描述QT中的文件流(QTextStream)和数据流(QDataStream)的区别 四、描述QT的TCP通讯流程 服务端:(QTcpServer) 客户端:(QTcpSocket…...

springboot+vue家乡特色推荐系统(源码+文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的家乡特色推荐系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 💕💕作者:风…...

在Shell脚本中通过ssh从脚本运行函数
文章目录 在Shell脚本中通过ssh从脚本运行函数declare -f 和typset -f,这两个命令有什么区别declare -f 和typset -f,这两个命令可以通过ssh运行脚本中的函数吗如果我有main.sh和util.sh,并且在main.sh中引用了util.sh,该怎么办&a…...

简单学习一下 MyBatis 动态SQL使用及原理
MyBatis 是一个优秀的持久层框架,它提供了丰富的 SQL 映射功能,可以让我们通过 XML 或注解方式来定义 SQL 语句。它很大程度上简化了数据库操作,提高了开发效率。动态 SQL 是其中一个非常重要的功能,可以让我们根据不同的条件动态…...
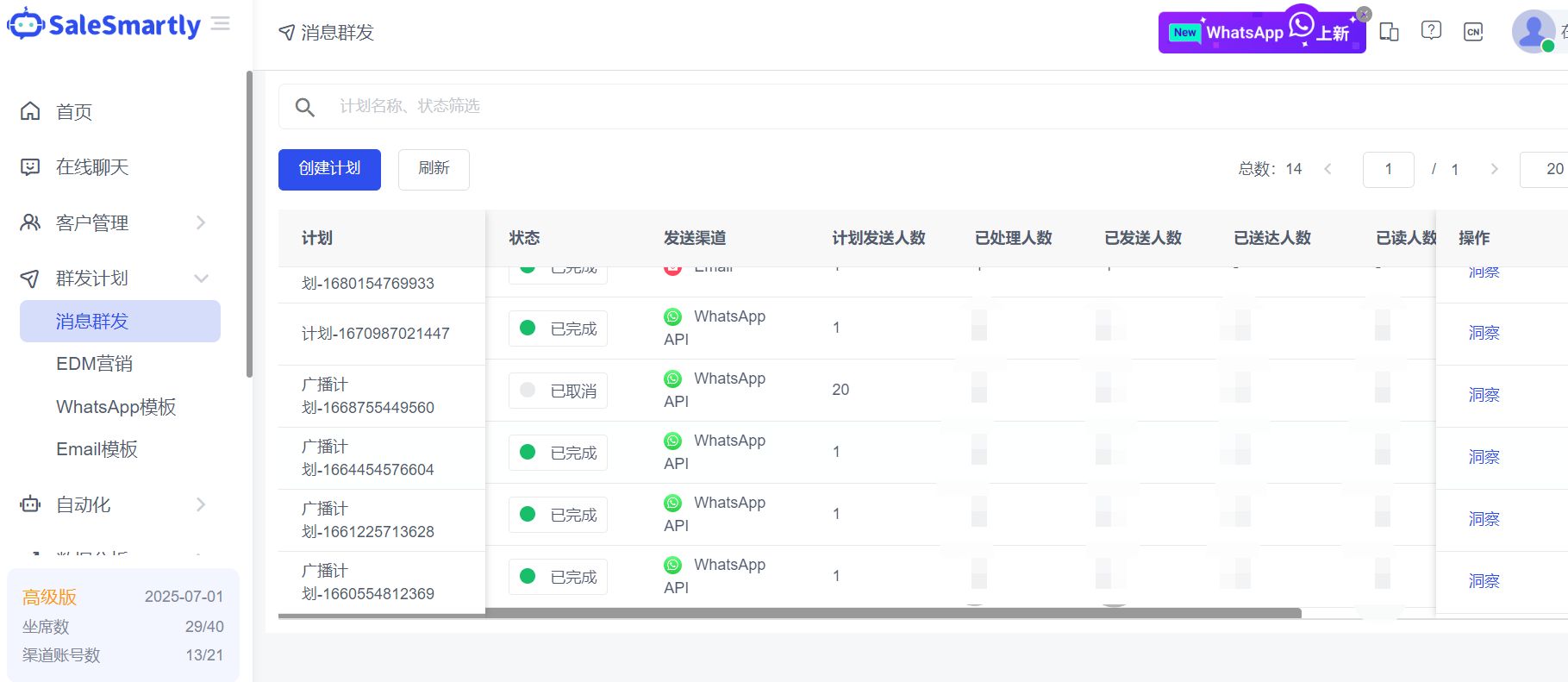
WhatsApp如何让客户参与变得更简单?
WhatsApp对你的品牌来说可能和Twitter和Facebook一样重要,你可能已经把它们纳入你的社交媒体战略。 是的,WhatsApp不仅仅可以用来给同事发短信或与远方的亲戚视频聊天,它也适用于商业。 在发展WhatsApp业务时,小企业主得到了最优…...
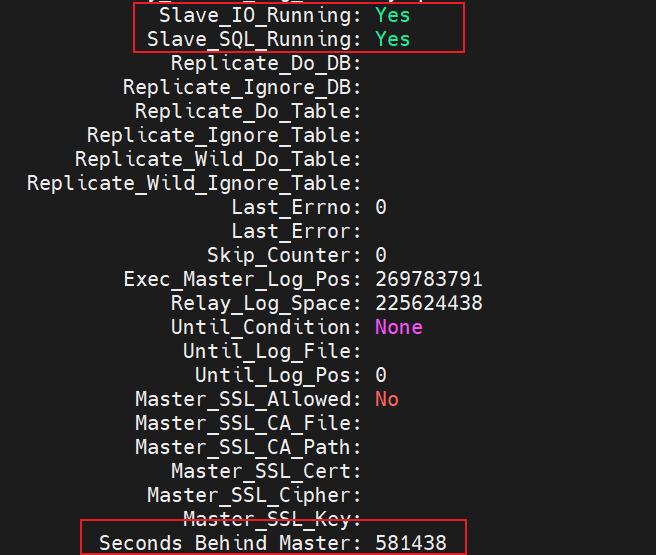
记一次 MySQL 主从同步异常的排查记录,百转千回
本文主要内容如下: 一、现象 最近项目的测试环境遇到一个主备同步的问题: 备库的同步线程停止了,无法同步主库的数据更改。 备库报错如下: 完整的错误信息: Relay log read failure: Could not parse relay log even…...

Cpython的多线程技术之痛
历史原因 在Python官网下载的默认解释器是采用C语言编写的Cpython解释器。在Python语言开发之初,计算机都是单核CPU,每个单核CPU同一时刻只能运行一个线程。为了模拟多线程工作,这里采用了模拟机制,让不同线程根据时间片段&#…...
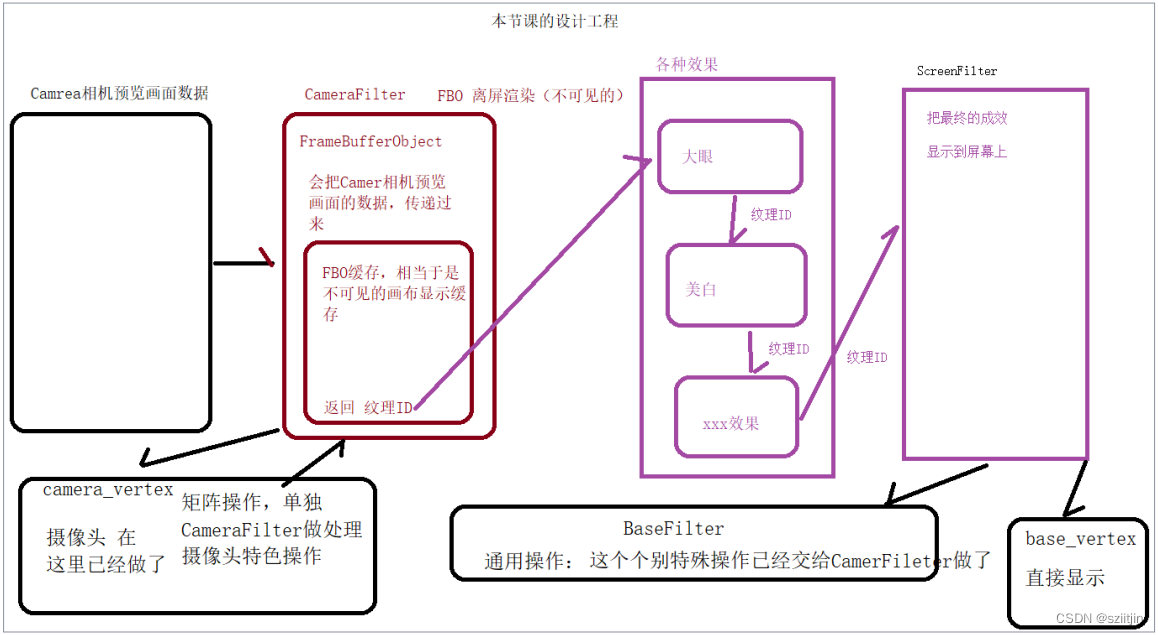
NDK OpenGL离屏渲染与工程代码整合
NDK系列之OpenGL离屏渲染与工程代码整合,本节主要是对上一节OpenGL渲染画面效果代码进行封装设计,将各种特效代码进行分离解耦,便于后期增加其他特效。 实现效果: 实现逻辑: 1.封装BaseFilter过滤器基类,…...

Python基础入门编程代码练习(二)
一、求1~100之间不能被3整除的数之和 循环条件:i<100循环操作 实现代码如下: def sums():sum 0for num in range(1, 101):if num % 3 ! 0:sum numprint("1~100之间不能被3整除的数之和为:%s" % (sum))sums() print("1~…...

C# | 对象池
对象池 文章目录 对象池前言什么是对象池对象池的优点对象池的缺点 实现思路示例代码 结束语 前言 当我们开发一个系统或者应用程序时,我们通常需要创建很多的对象,这些对象可能是线程、内存、数据库连接、文件句柄等等。在某些情况下,我们需…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
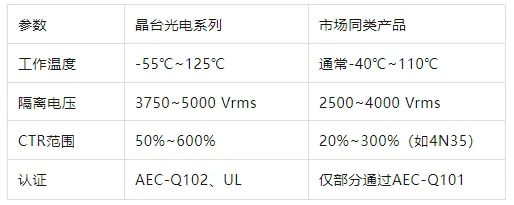
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
