微积分python基础
微积分基础(python)
文章目录
- 微积分基础(python)
- 1 函数与极限
- 2 求导与微分
- 3 不定积分
- 4 定积分
1 函数与极限
# 导入sympy库
from sympy import *
# 将x符号化
x = Symbol("x")
x
x \displaystyle x x
# 利用sympy中solve函数求解方程
X = solve(x**2-10*x+21,x)
X
print("原方程的解为:",X)
原方程的解为: [3, 7]
# 定义集合
A = set("12345")
B = set("123")
print("集合AB的并为:",A | B)
print("集合AB的交为:",A & B)
print("集合AB的差为:",A - B)
集合AB的并为: {'4', '2', '1', '5', '3'}
集合AB的交为: {'1', '3', '2'}
集合AB的差为: {'4', '5'}
# 自变量趋近无穷
n = Symbol("n")
s = n**2/(n**2+1)
result = limit(s,n,oo)
print("数列极限为:",result)
数列极限为: 1
# 自变量趋近有限值
x = Symbol("x")
s = (2-5*x**2)/(2*x+1)
print("函数极限为:",limit(s,x,-1/2))
函数极限为: oo
# 自变量趋近无穷大
x = Symbol("x")
s = (x+x**3)/(6*x**3)
print("函数极限为:",limit(s,x,oo))
函数极限为: 1/6
2 求导与微分
# 导入sympy库
from sympy import *
# 常数导数
x = Symbol("x")
C = 2
y = C
diff(y,x)
0 \displaystyle 0 0
# 幂函数导数
x = Symbol("x")
mu = Symbol("mu")
y = x**mu
diff(y,x)
μ x μ x \displaystyle \frac{\mu x^{\mu}}{x} xμxμ
# 指数函数求导
a = Symbol("a")
x = Symbol("x")
y = a**x
diff(y,x)
a x log ( a ) \displaystyle a^{x} \log{\left(a \right)} axlog(a)
# 对数函数求导
a = Symbol("a")
x = Symbol("x")
y = log(x,a)
diff(y,x)
1 x log ( a ) \displaystyle \frac{1}{x \log{\left(a \right)}} xlog(a)1
# 正弦求导
x = Symbol("x")
y = sin(x)
diff(y,x)
cos ( x ) \displaystyle \cos{\left(x \right)} cos(x)
# 反正弦函数求导
x = Symbol("x")
y = asin(x)
diff(y,x)
1 1 − x 2 \displaystyle \frac{1}{\sqrt{1 - x^{2}}} 1−x21
# 求导四则运算
x = Symbol("x")
u = log(x,a)
v = x**2+1
y = u+v
diff(y,x)
2 x + 1 x log ( a ) \displaystyle 2 x + \frac{1}{x \log{\left(a \right)}} 2x+xlog(a)1
y = u - v
diff(y,x)
− 2 x + 1 x log ( a ) \displaystyle - 2 x + \frac{1}{x \log{\left(a \right)}} −2x+xlog(a)1
y = u*v
diff(y,x)
2 x log ( x ) log ( a ) + x 2 + 1 x log ( a ) \displaystyle \frac{2 x \log{\left(x \right)}}{\log{\left(a \right)}} + \frac{x^{2} + 1}{x \log{\left(a \right)}} log(a)2xlog(x)+xlog(a)x2+1
y = u/v
diff(y,x)
− 2 x log ( x ) ( x 2 + 1 ) 2 log ( a ) + 1 x ( x 2 + 1 ) log ( a ) \displaystyle - \frac{2 x \log{\left(x \right)}}{\left(x^{2} + 1\right)^{2} \log{\left(a \right)}} + \frac{1}{x \left(x^{2} + 1\right) \log{\left(a \right)}} −(x2+1)2log(a)2xlog(x)+x(x2+1)log(a)1
# 复合函数求导
x = Symbol("x")
u = Symbol("u")
u = x**2
y =sin(u)
diff(y,x)
2 x cos ( x 2 ) \displaystyle 2 x \cos{\left(x^{2} \right)} 2xcos(x2)
# 链式求导
x = Symbol("x")
u = Symbol("u")
v = Symbol("v")
v = sin(x)**2
u = tan(v)**2
y = log(u)**2
diff(y,x)
8 ( tan 2 ( sin 2 ( x ) ) + 1 ) log ( tan 2 ( sin 2 ( x ) ) ) sin ( x ) cos ( x ) tan ( sin 2 ( x ) ) \displaystyle \frac{8 \left(\tan^{2}{\left(\sin^{2}{\left(x \right)} \right)} + 1\right) \log{\left(\tan^{2}{\left(\sin^{2}{\left(x \right)} \right)} \right)} \sin{\left(x \right)} \cos{\left(x \right)}}{\tan{\left(\sin^{2}{\left(x \right)} \right)}} tan(sin2(x))8(tan2(sin2(x))+1)log(tan2(sin2(x)))sin(x)cos(x)
# 二阶求导
diff(y,x,2)
( tan 2 ( sin ( x ) ) + 1 ) ( − ( tan 2 ( sin ( x ) ) + 1 ) cos 2 ( x ) tan 2 ( sin ( x ) ) − sin ( x ) tan ( sin ( x ) ) + 2 cos 2 ( x ) ) \displaystyle \left(\tan^{2}{\left(\sin{\left(x \right)} \right)} + 1\right) \left(- \frac{\left(\tan^{2}{\left(\sin{\left(x \right)} \right)} + 1\right) \cos^{2}{\left(x \right)}}{\tan^{2}{\left(\sin{\left(x \right)} \right)}} - \frac{\sin{\left(x \right)}}{\tan{\left(\sin{\left(x \right)} \right)}} + 2 \cos^{2}{\left(x \right)}\right) (tan2(sin(x))+1)(−tan2(sin(x))(tan2(sin(x))+1)cos2(x)−tan(sin(x))sin(x)+2cos2(x))
# 计算函数拐点
from sympy import *
x = Symbol("x")
y = 2*x**3-12*x**2+18*x-2
# 一阶导数
df1 = diff(y,x)
df1
6 x 2 − 24 x + 18 \displaystyle 6 x^{2} - 24 x + 18 6x2−24x+18
# 二阶导数
df2 = diff(y,x,2)
df2
12 ( x − 2 ) \displaystyle 12 \left(x - 2\right) 12(x−2)
print("二阶导数取值为0的点为",solve(df2))
print("拐点值为",y.subs(x,2))
二阶导数取值为0的点为 [2]
拐点值为 2
# 第一充分条件求极值点
from sympy import *
x = Symbol("x")
y = (x+3)**2*(x-1)**3
df = diff(y,x)
print("函数驻点为:",solve(df,x))
函数驻点为: [-3, -7/5, 1]
print("函数极值为",y.subs(x,-3),y.subs(x,-7/5),y.subs(x,1))
函数极值为 0 -35.3894400000000 0
# 第二充分条件求极值点
from sympy import *
y = 2*x**3-6*x**2+7
df = diff(y,x)
print("函数极值点为",solve(df,x))
函数极值点为 [0, 2]
df2 = diff(y,x,2)
print("二阶导数驻点的值为:",df2.subs(x,0),df2.subs(x,2))
二阶导数驻点的值为: -12 12
print("函数的极值为",y.subs(x,0),y.subs(x,2))
函数的极值为 7 -1
3 不定积分
x = Symbol("x")
f = cos(x)
integrate(f,x)
sin ( x ) \displaystyle \sin{\left(x \right)} sin(x)
x = Symbol("x")
f = 1/(1+x**2)
integrate(f,x)
atan ( x ) \displaystyle \operatorname{atan}{\left(x \right)} atan(x)
x = Symbol("x")
f = exp(x)*sin(x)
integrate(f,x)
e x sin ( x ) 2 − e x cos ( x ) 2 \displaystyle \frac{e^{x} \sin{\left(x \right)}}{2} - \frac{e^{x} \cos{\left(x \right)}}{2} 2exsin(x)−2excos(x)
4 定积分
x = Symbol("x")
a = Symbol("a")
b = Symbol("b")
y = sin(a*x)*cos(b*x)
integrate(y,(x,a,b))
{ 0 for ( a = 0 ∧ b = 0 ) ∨ ( a = 0 ∧ a = b ∧ b = 0 ) ∨ ( a = 0 ∧ a = − b ∧ b = 0 ) ∨ ( a = 0 ∧ a = − b ∧ a = b ∧ b = 0 ) cos 2 ( b 2 ) 2 b − cos 2 ( a b ) 2 b for ( a = 0 ∧ a = − b ) ∨ ( a = − b ∧ a = b ) ∨ ( a = − b ∧ b = 0 ) ∨ ( a = 0 ∧ a = − b ∧ a = b ) ∨ ( a = − b ∧ a = b ∧ b = 0 ) ∨ a = − b − cos 2 ( b 2 ) 2 b + cos 2 ( a b ) 2 b for ( a = 0 ∧ a = b ) ∨ ( a = b ∧ b = 0 ) ∨ a = b a cos ( a 2 ) cos ( a b ) a 2 − b 2 − a cos ( b 2 ) cos ( a b ) a 2 − b 2 + b sin ( a 2 ) sin ( a b ) a 2 − b 2 − b sin ( b 2 ) sin ( a b ) a 2 − b 2 otherwise \displaystyle \begin{cases} 0 & \text{for}\: \left(a = 0 \wedge b = 0\right) \vee \left(a = 0 \wedge a = b \wedge b = 0\right) \vee \left(a = 0 \wedge a = - b \wedge b = 0\right) \vee \left(a = 0 \wedge a = - b \wedge a = b \wedge b = 0\right) \\\frac{\cos^{2}{\left(b^{2} \right)}}{2 b} - \frac{\cos^{2}{\left(a b \right)}}{2 b} & \text{for}\: \left(a = 0 \wedge a = - b\right) \vee \left(a = - b \wedge a = b\right) \vee \left(a = - b \wedge b = 0\right) \vee \left(a = 0 \wedge a = - b \wedge a = b\right) \vee \left(a = - b \wedge a = b \wedge b = 0\right) \vee a = - b \\- \frac{\cos^{2}{\left(b^{2} \right)}}{2 b} + \frac{\cos^{2}{\left(a b \right)}}{2 b} & \text{for}\: \left(a = 0 \wedge a = b\right) \vee \left(a = b \wedge b = 0\right) \vee a = b \\\frac{a \cos{\left(a^{2} \right)} \cos{\left(a b \right)}}{a^{2} - b^{2}} - \frac{a \cos{\left(b^{2} \right)} \cos{\left(a b \right)}}{a^{2} - b^{2}} + \frac{b \sin{\left(a^{2} \right)} \sin{\left(a b \right)}}{a^{2} - b^{2}} - \frac{b \sin{\left(b^{2} \right)} \sin{\left(a b \right)}}{a^{2} - b^{2}} & \text{otherwise} \end{cases} ⎩ ⎨ ⎧02bcos2(b2)−2bcos2(ab)−2bcos2(b2)+2bcos2(ab)a2−b2acos(a2)cos(ab)−a2−b2acos(b2)cos(ab)+a2−b2bsin(a2)sin(ab)−a2−b2bsin(b2)sin(ab)for(a=0∧b=0)∨(a=0∧a=b∧b=0)∨(a=0∧a=−b∧b=0)∨(a=0∧a=−b∧a=b∧b=0)for(a=0∧a=−b)∨(a=−b∧a=b)∨(a=−b∧b=0)∨(a=0∧a=−b∧a=b)∨(a=−b∧a=b∧b=0)∨a=−bfor(a=0∧a=b)∨(a=b∧b=0)∨a=botherwise
x = Symbol("x")
f = sin(x)
integrate(f,(x,0,pi))
2 \displaystyle 2 2
相关文章:

微积分python基础
微积分基础(python) 文章目录 微积分基础(python)1 函数与极限2 求导与微分3 不定积分4 定积分 1 函数与极限 # 导入sympy库 from sympy import * # 将x符号化 x Symbol("x") xx \displaystyle x x # 利用sympy中solve函数求解方程 X solve(x**2-10*x21,x) X pri…...
)
Redis缓存数据库(一)
目录 一、概述 1、Redis 2、Redis的安装 Redis Windows环境设置 3、String: 字符串 3.1、字符串 3.2、数值 3.3、bitmap 4、Hash: 散列 5、List: 列表 6、Set: 集合 7、Sorted Set: 有序集合 一、概述 常识: 磁盘:1.寻址:ms&…...

物联网|uart串口相关寄存器|波特率设置及计算|发送处理代码|串口接收中断处理函数|物联网之蓝牙4.0 BLE基础-学习笔记(7)
文章目录 13 uart串口基础开发基本电路图:实验相关寄存器波特率设置及计算计算过程:设置中断发送处理代码串口接收中断处理函数main.c 13 uart串口基础开发 基本电路图: 实验相关寄存器 相关寄存器UxCSR、UxCSR、UxGCR、UxBUF、UxBAUD、CLK…...

有数·智享未来 | 新华三重磅发布绿洲平台3.0
5月10日,紫光股份旗下新华三集团以“有数智享未来”为主题,成功举办绿洲平台3.0新品发布会。全新一代绿洲平台实现内核进阶,以五大技术能力升级、五大行业方案沉淀、六类服务能力保障,三位一体构筑更领先的用数底座、更落地的用数…...
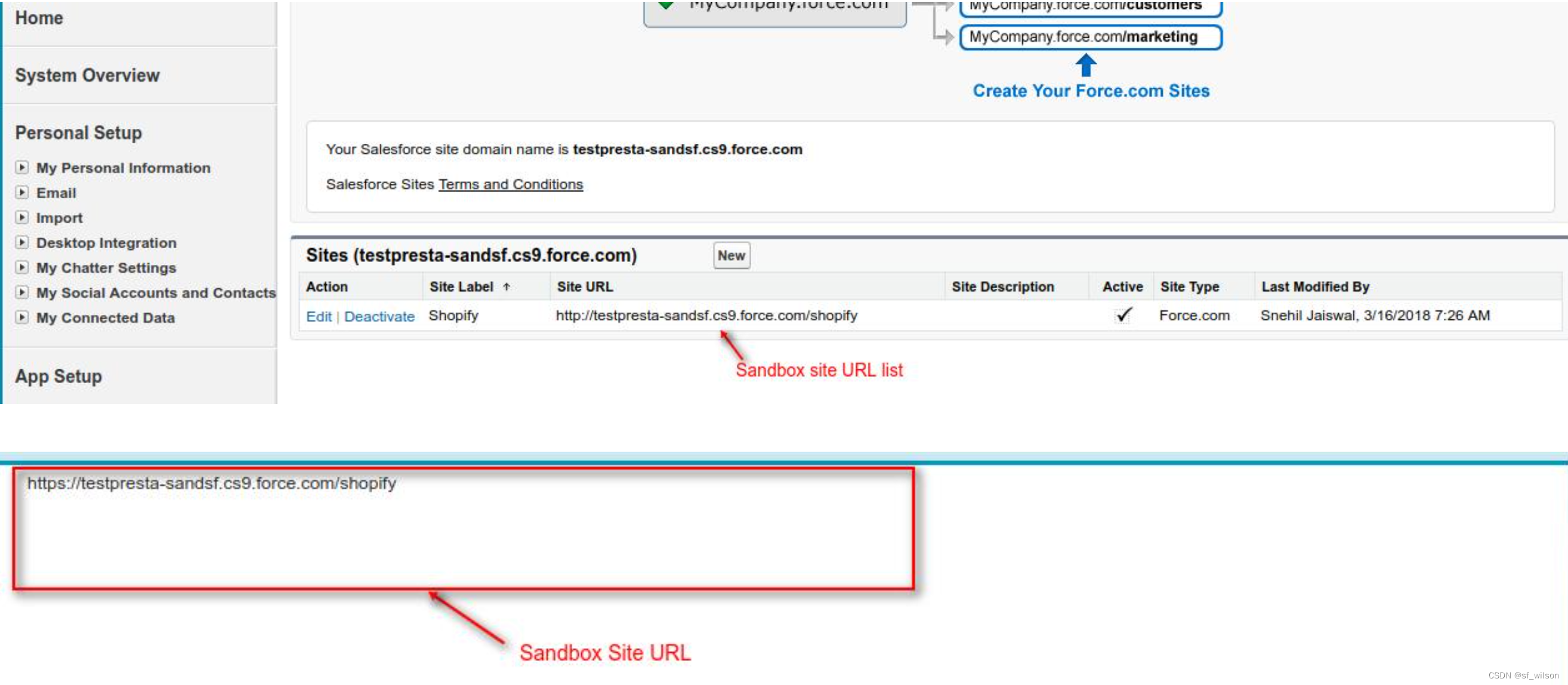
在Apex中获取Site URL
Foreword 目前SF暂未提供直接有效的方法在Apex获取SiteURL,我们可以在Idea (Access URL for a Site or Community from Apex)页面投票,除了下面提供的一种hack思路,当然也可以通过Custom Label手动维护。 Format of Site URL Sandbox site …...
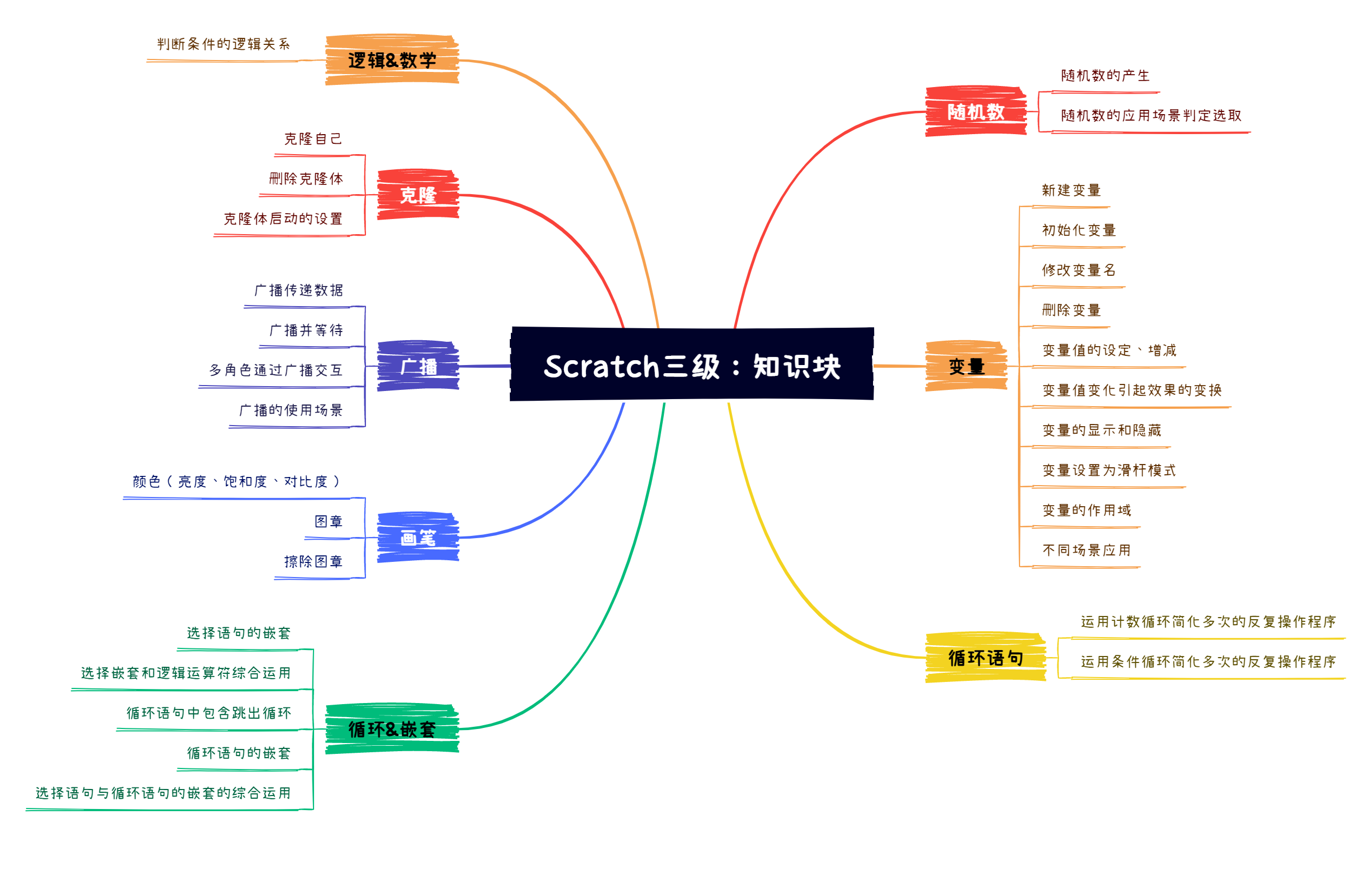
【电子学会】2023年03月图形化三级 -- 比大小.md
文章目录 比大小1. 准备工作2. 功能实现3. 设计思路与实现(1)角色分析(2)背景分析(3)所用积木块介绍a. 运动类b. 外观类c. 事件类d. 控制类e. 运算类f. 变量类 (4)角色、舞台背景设置…...
Kali-linux使用Nessus
Nessus号称是世界上最流行的漏洞扫描程序,全世界有超过75000个组织在使用它。该工具提供完整的电脑漏洞扫描服务,并随时更新其漏洞数据库。Nessus不同于传统的漏洞扫描软件,Nessus可同时在本机或远端上遥控,进行系统的漏洞分析扫描…...

青训营 x 训练营结营测试题目(前端方向)
文章目录 📋前言🎯选择题(含多选)📝最后 📋前言 这篇文章的内容是23年6月青训营 x 训练营结营题目,题目一共有25题,题目类型为选择题,包括了单选题和多选题,…...
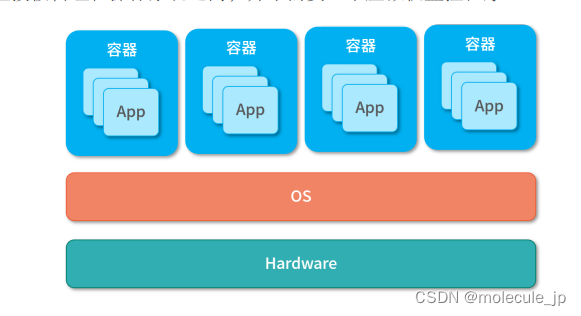
虚拟化技术介绍-VMware和Docker的区别
都说今天是一个云时代,其实云的本质就是由基础架构提供商提供基础架构,应用开发商不再关心基础架构。我们可以类比人类刚刚发明电的时候,工厂需要自己建电站,而现在只需要电线和插座就可以使用电。云时代让我们可以在分钟、甚至秒…...
TinyHttpd 运行过程出现的问题
最近拉了个 TinyHttpd 的工程下来,不过好像各个都有些改动,最后挑了篇阅读量最多的。工程也是从这里面给的链接下载的。 参考自:https://blog.csdn.net/jcjc918/article/details/42129311 拿下来在编译运行前,按这里说的&#x…...
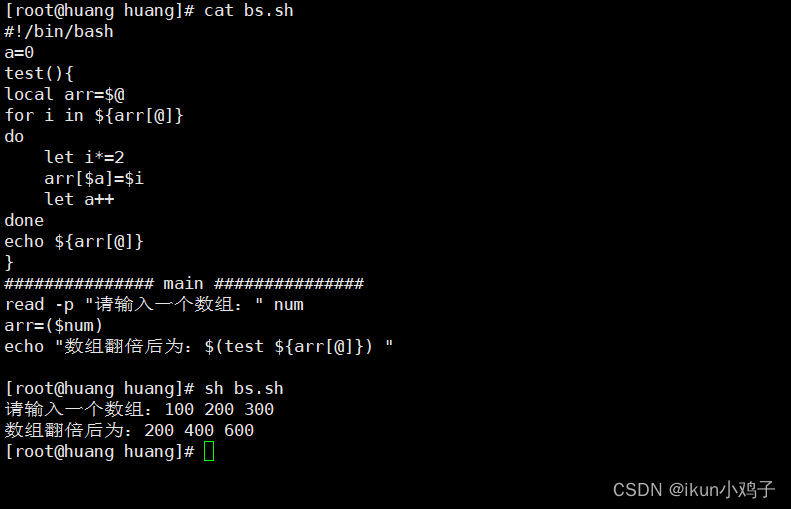
【Linux】shell编程—数组
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、shell数组1,数组的概念2.数组的定义 二、Shell数组操作1. 获取数组的所有元素的列表2. 获取数组的所有元素下标3.取数组的元素个数4. 获取数组的某个元素的值5.…...

Maven仓库与Maven插件
目录 Maven 仓库 本地仓库 中央仓库 远程仓库 Maven 依赖搜索顺序 Maven 阿里云(Aliyun)仓库 gradle 配置指南 Maven 插件 插件类型 实例 Maven 仓库 在 Maven 的术语中,仓库是一个位置(place)。 Maven 仓库是项目中依赖的第三方库…...
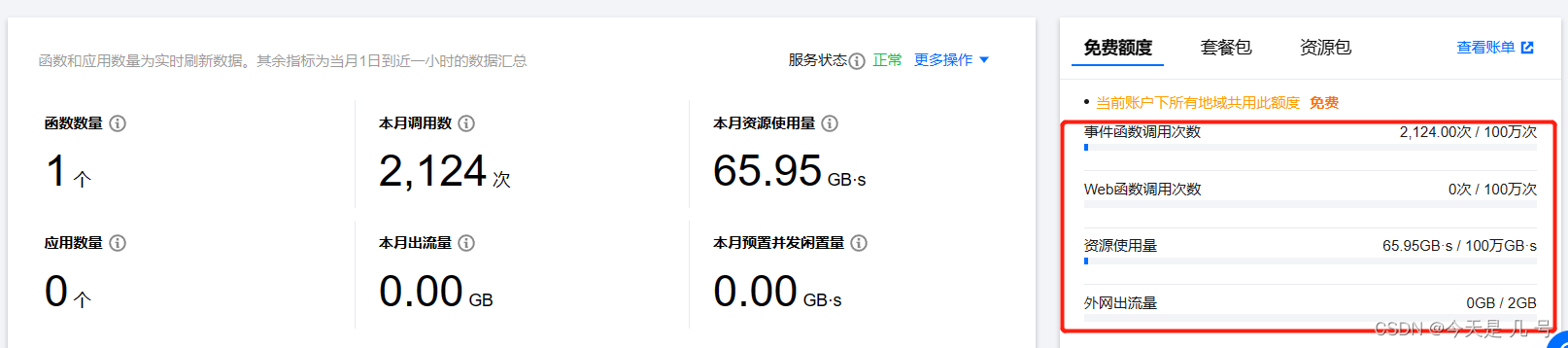
【溯源反制】CDN域前置云函数-流量分析|溯源
文章目录 CDN隐藏C2地址环境搭建上传至威胁感知平台直接分析使用DNSQuerySniffer和Process Monitor定位进程网络流量分析文件属性(IDAPro Ollydbg) 域前置隐藏环境搭建威胁感知流量分析 云服务API网关/云函数云函数使用HTTPcs的流量可以简单的分为三个阶段 云函数使用HTTPS 总结…...

【Vue】学习笔记-全局事件总线
全局事件总线(GlobalEventBus) 一种可以在任意组件通信的方式,本质上就是一个对象,它必须满足以下条件 所有的组件对象都必须能看见他这个对象必须能够使用$ on $ emit $ off方法取绑定、触发和解绑事件 使用步骤 定义全局事件总线 //创建VUE new V…...

MATLAB数值运算(六)
目录 实验目的 实验内容 原创代码,仅供参考,不要直接CV呀 ~_~ 实验目的 1)掌握定义符号对象和创建符号表达式的方法; 2)掌握符号运算基本命令和规则; 3)掌握符号表达式的运算法则以及符号矩阵…...

某医院Pad网络故障分析
分析背景 某医院为了加强信息安全管理,防止病人隐私信息泄露,采用部署“零信任”安全架构设计理念的企业移动安全支撑平台方案。 但在部署前期测试时,遇到了严重的性能问题。 在本次测试环境中,通过PAD访问患者转运业务&#x…...
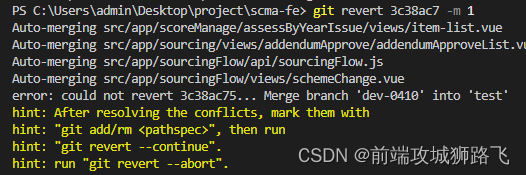
git 撤销中间某次提交,保留其他提交的方法
今天上班脑抽了,吧test直接合到了uat,因为项目近期就我一个人开发,自己拉个三个分支再改不同的东西,最后都是发到test分支发测试,发生产的时候一个个和嫌麻烦,直接吧test分支怼到了uat,结果生产就出问题了&…...
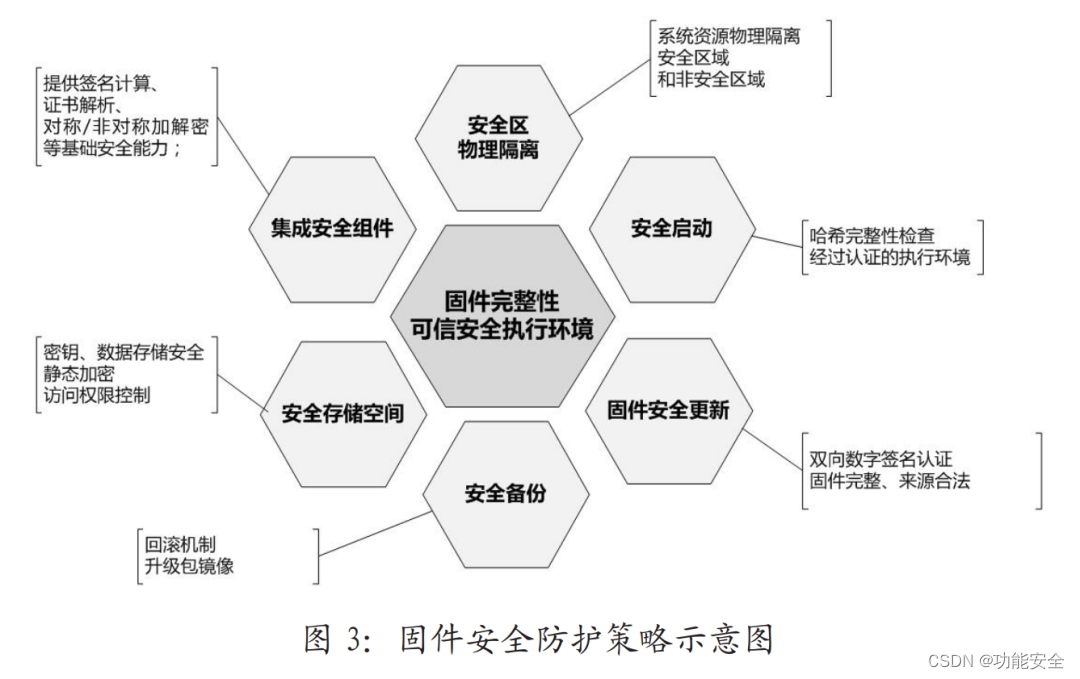
空中下载技术(OTA)电控信息安全
随着汽车电子控制系统功能复杂度和数据颗粒度呈阶梯式增加,其发展速度逐渐超越网络安全防护方法、技术和标准的发展,现阶段汽车电子正面临巨大的网络信息安全风险,对功能安全的潜在影响也仍在探索和解决中,信息安全问题已经成为影…...

数据库sql语句(count(*)和count(字段))
例题: 创建如下两张表 分别命名为books和persons (1)按照书名,姓名的顺序列出字里包含‘德’字的人物的姓名,书名和字。 select name 姓名,bookname 书名,style 字 from books,persons where style like %德% and bo…...
短视频矩阵源码系统
短视频矩阵源码系统开发要则: 1. 需求分析:对短视频平台的需求进行全面分析,确立系统开发目标和方向。 2. 技术选型:选用最适合的技术开发短视频矩阵系统,如前端框架、数据库、服务器等。 3. 系统设计:按…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
