(数字图像处理MATLAB+Python)第七章图像锐化-第一、二节:图像锐化概述和微分算子
文章目录
- 一:图像边缘分析
- 二:一阶微分算子
- (1)梯度算子
- A:定义
- B:边缘检测
- C:示例
- D:程序
- (2)Robert算子
- A:定义
- B:示例
- C:程序
- (3)Sobel算子
- A:定义
- B:示例
- C:程序
- (4)Prewitt算子
- A:定义
- B:示例
- C:程序
- 三:二阶微分算子
- (1)定义
- (2)示例
- (3)程序
图像锐化:是一种用于改善图像质量的技术,它可以增强图像中的高频细节信息,从而使得图像更加清晰和有视觉冲击力。在图像处理和计算机视觉中,图像锐化通常被用于特征提取、图像增强、目标识别等应用中

一:图像边缘分析
图像边缘分析:是一种用于在图像中找到明显的边缘或轮廓的技术,它可以帮助识别图像中的物体边界、内部结构和纹理等特征。在图像处理和计算机视觉中,边缘分析通常被用于物体检测、目标跟踪、图像分割等应用中
图像中的边缘主要有以下几种类型
- 细线型边缘:
- 突变型边缘:
- 渐变型边缘:

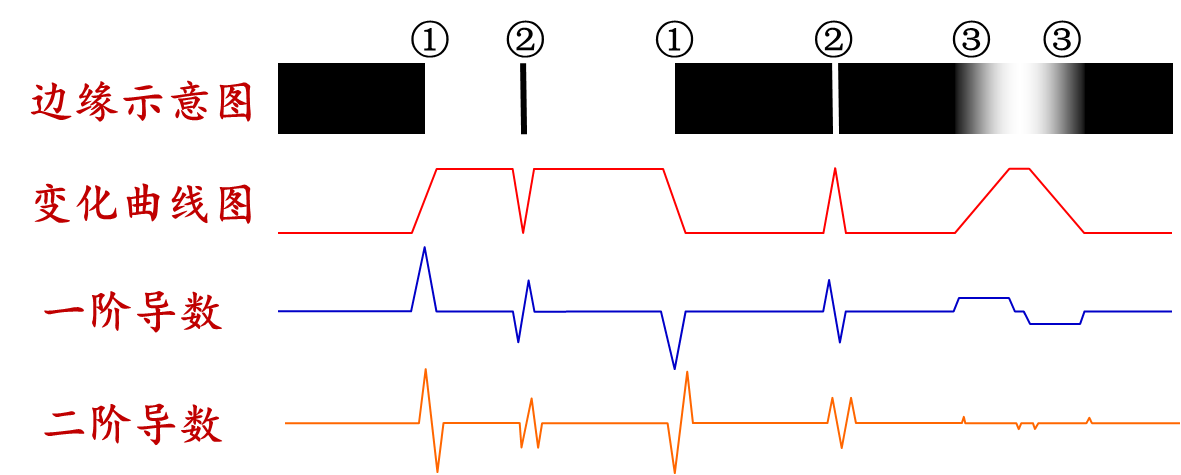
如下图,各种边缘检测方法
- 细线型边缘:检测一阶微分过0点,二阶微分极值点
- 突变型边缘:检测一阶微分极值点,二阶微分过0点
- 渐变型边缘:难检测,二阶微分信息略多于一阶微分
二:一阶微分算子
(1)梯度算子
A:定义
梯度算子:是一类用于图像边缘检测和特征提取的算法,它们基于图像灰度值的变化来计算图像中各个位置的梯度信息,用于找到图像中明显的边缘或特征。对于函数图像 f ( x , y ) f(x,y) f(x,y),它在 ( x , y ) (x,y) (x,y)处的梯度为
G [ f ( x , y ) ] = [ ∂ f ∂ x ∂ f ∂ y ] T G[f(x, y)]=\left[\begin{array}{ll}\frac{\partial f}{\partial x} & \frac{\partial f}{\partial y}\end{array}\right]^{T} G[f(x,y)]=[∂x∂f∂y∂f]T
用梯度的幅度来代替,则为
G [ f ( x , y ) ] = [ ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 ] 1 2 或 G [ f ( x , y ) ] = ∣ ∂ f ∂ x ∣ + ∣ ∂ f ∂ y ∣ G[f(x, y)]=\left[\left(\frac{\partial f}{\partial x}\right)^{2}+\left(\frac{\partial f}{\partial y}\right)^{2}\right]^{\frac{1}{2}} \text { 或 } G[f(x, y)]=\left|\frac{\partial f}{\partial x}\right|+\left|\frac{\partial f}{\partial y}\right| G[f(x,y)]=[(∂x∂f)2+(∂y∂f)2]21 或 G[f(x,y)]= ∂x∂f + ∂y∂f
离散的数字矩阵,用差分来代替微分,其中 g ( x , y ) g(x,y) g(x,y)称为梯度图像
∂ f ∂ x = Δ f Δ x = f ( x + 1 , y ) − f ( x , y ) x + 1 − x = f ( x + 1 , y ) − f ( x , y ) ∂ f ∂ y = Δ f Δ y = f ( x , y + 1 ) − f ( x , y ) y + 1 − y = f ( x , y + 1 ) − f ( x , y ) g ( x , y ) = ∣ f ( x + 1 , y ) − f ( x , y ) ∣ + ∣ f ( x , y + 1 ) − f ( x , y ) ∣ \begin{array}{l}\frac{\partial f}{\partial x}=\frac{\Delta f}{\Delta x}=\frac{f(x+1, y)-f(x, y)}{x+1-x}=f(x+1, y)-f(x, y) \\\frac{\partial f}{\partial y}=\frac{\Delta f}{\Delta y}=\frac{f(x, y+1)-f(x, y)}{y+1-y}=f(x, y+1)-f(x, y) \\g(x, y)=|f(x+1, y)-f(x, y)|+|f(x, y+1)-f(x, y)|\end{array} ∂x∂f=ΔxΔf=x+1−xf(x+1,y)−f(x,y)=f(x+1,y)−f(x,y)∂y∂f=ΔyΔf=y+1−yf(x,y+1)−f(x,y)=f(x,y+1)−f(x,y)g(x,y)=∣f(x+1,y)−f(x,y)∣+∣f(x,y+1)−f(x,y)∣
B:边缘检测
- 对梯度图像进行阈值化,检测局部变化极值
固定边界灰度:
g ( x , y ) = { L G G [ f ( x , y ) ] ≥ T f ( x , y ) 其他 g(x, y)=\left\{\begin{array}{lc}L_{G} & G[f(x, y)] \geq T \\f(x, y) & \text { 其他 }\end{array}\right. g(x,y)={LGf(x,y)G[f(x,y)]≥T 其他
突出边界:
g ( x , y ) = { G [ f ( x , y ) ] G [ f ( x , y ) ] ≥ T f ( x , y ) 其他 g(x, y)=\left\{\begin{array}{lc}G[f(x, y)] & G[f(x, y)] \geq T \\f(x, y) & \text { 其他 }\end{array}\right. g(x,y)={G[f(x,y)]f(x,y)G[f(x,y)]≥T 其他
二值化边界与背景:
g ( x , y ) = { L G G [ f ( x , y ) ] ≥ T L B 其他 g(x, y)=\left\{\begin{array}{lc}L_{G} & G[f(x, y)] \geq T \\L_{B} & \text { 其他 }\end{array}\right. g(x,y)={LGLBG[f(x,y)]≥T 其他
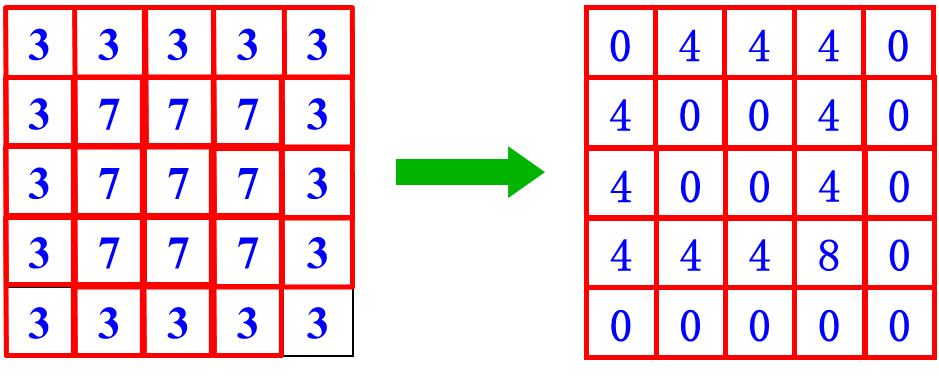
C:示例
如下为一个计算示例
D:程序

matlab实现:
Image=im2double(rgb2gray(imread('lotus.jpg')));
subplot(131),imshow(Image),title('原图像');
[h,w]=size(Image);
edgeImage=zeros(h,w);
for x=1:w-1for y=1:h-1edgeImage(y,x)=abs(Image(y,x+1)-Image(y,x))+abs(Image(y+1,x)-Image(y,x));end
end
subplot(132),imshow(edgeImage),title('梯度图像');
sharpImage=Image+edgeImage;
subplot(133),imshow(sharpImage),title('锐化图像');
Python实现:
import cv2
import numpy as np
from matplotlib import pyplot as plt# 读取图像
img = cv2.imread('lotus.jpg')
# 将图像转为灰度图像并将像素值缩放到[0,1]之间
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gray = gray.astype(np.float64) / 255# 显示原图像
plt.subplot(131)
plt.imshow(gray, cmap='gray')
plt.title('原图像')# 计算梯度图像
h, w = gray.shape
edge_img = np.zeros((h, w))
for x in range(w-1):for y in range(h-1):edge_img[y,x] = abs(gray[y,x+1]-gray[y,x]) + abs(gray[y+1,x]-gray[y,x])# 显示梯度图像
plt.subplot(132)
plt.imshow(edge_img, cmap='gray')
plt.title('梯度图像')# 锐化图像
sharp_img = gray + edge_img
sharp_img = np.clip(sharp_img, 0, 1)# 显示锐化图像
plt.subplot(133)
plt.imshow(sharp_img, cmap='gray')
plt.title('锐化图像')# 显示所有图像
plt.show()(2)Robert算子
A:定义
Robert算子:是一种边缘检测算子,其原理基于图像中像素值的差异。该算子的实现使用了两个 2 × 2 2 \times 2 2×2 的卷积核 G x G_x Gx 和 G y G_y Gy,分别计算像素点 ( x , y ) (x,y) (x,y) 和 ( x + 1 , y + 1 ) (x+1,y+1) (x+1,y+1) 之间的灰度差异。具体来说, G x G_x Gx 和 G y G_y Gy 的取值如下
[ 1 0 0 − 1 ] 和 [ 0 1 − 1 0 ] \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix} 和\begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix} [100−1]和[0−110]
然后,对于输入图像 I I I,可以通过以下公式计算其边缘强度 E E E
*表示卷积运算
E ( x , y ) = ( I ( x , y ) ∗ G x ) 2 + ( I ( x , y ) ∗ G y ) 2 E(x, y)=\sqrt{\left(I(x, y) * G_{x}\right)^{2}+\left(I(x, y) * G_{y}\right)^{2}} E(x,y)=(I(x,y)∗Gx)2+(I(x,y)∗Gy)2
最终得到的边缘强度 E E E 可以用来检测图像中的边缘,边缘通常在 E E E 取得较大值的地方出现。此外,为了提高计算效率,通常也可以使用预先计算好的卷积核来实现 Robert 算子
B:示例
如下图为一计算示例

C:程序

edge函数:用于在图像中检测边缘并生成二值化的边缘图像。该函数语法如下
BW = edge(I, method, threshold, direction)参数含义如下
I:输入图像,可以是灰度图像或彩色图像。对于彩色图像,通常会先将其转换为灰度图像,然后再进行边缘检测method:边缘检测的方法,包括以下几种,默认值为'sobel''sobel':Sobel算子检测边缘'prewitt':Prewitt算子检测边缘'roberts':Roberts算子检测边缘'log':Laplacian of Gaussian算子检测边缘'zerocross':使用Laplacian算子和零交叉检测边缘'canny':使用Canny算子检测边缘
threshold:二值化的阈值,用于将检测到的边缘转换为二值化图像。对于Canny算子,此参数可以是包含两个元素的向量,分别表示低阈值和高阈值。默认值为0.2direction:边缘的检测方向,包括以下几种,默认值为'both''both':检测水平和垂直方向的边缘'horizontal':仅检测水平方向的边缘'vertical':仅检测垂直方向的边缘
matlab实现:
Image=im2double(rgb2gray(imread('lotus.jpg')));
% 将名为 lotus.jpg 的彩色图像读入并转换为灰度图像,然后将其类型转换为double型,存储在变量 Image 中。figure,imshow(Image),title('原图像');
% 显示原始图像BW= edge(Image,'roberts');
% 对图像进行 Robert 边缘检测,得到一个二值化的边缘图像,存储在变量 BW 中。figure,imshow(BW),title('边缘检测');
% 显示 Robert 边缘检测结果H1=[1 0; 0 -1];
H2=[0 1;-1 0];
% 定义两个 2×2 的卷积核 H1 和 H2,分别为 Robert 算子的两个分量。R1=imfilter(Image,H1);
R2=imfilter(Image,H2);
% 对原始图像分别使用 H1 和 H2 进行卷积操作,得到两个梯度图像 R1 和 R2。edgeImage=abs(R1)+abs(R2);
% 将 R1 和 R2 两个梯度图像的绝对值相加,得到最终的梯度图像,存储在变量 edgeImage 中。figure,imshow(edgeImage),title('Robert梯度图像');
% 显示 Robert 算子得到的梯度图像sharpImage=Image+edgeImage;
% 将原始图像与梯度图像相加,得到锐化后的图像,存储在变量 sharpImage 中。figure,imshow(sharpImage),title('Robert锐化图像');
% 显示锐化后的图像Python实现:
import cv2
import numpy as np
from matplotlib import pyplot as plt# 读入图像并转换为灰度图像
img = cv2.imread('lotus.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gray = gray.astype(np.float64) / 255.0# 显示原图像
plt.imshow(gray, cmap='gray')
plt.title('原图像')
plt.show()# 进行边缘检测
edge = cv2.Canny(gray, 100, 200)# 显示边缘检测结果
plt.imshow(edge, cmap='gray')
plt.title('边缘检测')
plt.show()# 定义两个 2×2 的卷积核 H1 和 H2,分别为 Robert 算子的两个分量
H1 = np.array([[1, 0], [0, -1]])
H2 = np.array([[0, 1], [-1, 0]])# 对原始图像分别使用 H1 和 H2 进行卷积操作,得到两个梯度图像 R1 和 R2
R1 = cv2.filter2D(gray, -1, H1)
R2 = cv2.filter2D(gray, -1, H2)# 将 R1 和 R2 两个梯度图像的绝对值相加,得到最终的梯度图像
edgeImage = cv2.addWeighted(cv2.convertScaleAbs(R1), 0.5, cv2.convertScaleAbs(R2), 0.5, 0)# 显示 Robert 算子得到的梯度图像
plt.imshow(edgeImage, cmap='gray')
plt.title('Robert梯度图像')
plt.show()# 将原始图像与梯度图像相加,得到锐化后的图像
sharpImage = cv2.addWeighted(gray, 1, edgeImage, 1, 0)# 显示锐化后的图像
plt.imshow(sharpImage, cmap='gray')
plt.title('Robert锐化图像')
plt.show()(3)Sobel算子
A:定义
Sobel算子:是一种常用的边缘检测算子,用于在数字图像中检测出边缘部分。它使用两个 3 × 3 3 \times 3 3×3的卷积核,分别对图像在 x x x和 y y y方向进行卷积操作,从而计算出每个像素点处的梯度大小和方向。 x x x和 y y y方向的卷积核可以表示为
H x = [ − 1 − 2 − 1 0 0 0 1 2 1 ] 和 H y = [ − 1 0 1 − 2 0 − 2 − 1 0 1 ] H_{x}=\begin{bmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1 \end{bmatrix}和H_{y}=\begin{bmatrix} -1 & 0 & 1\\ -2 & 0 & -2\\ -1 & 0 & 1 \end{bmatrix} Hx= −101−202−101 和Hy= −1−2−10001−21
对于一个灰度图像 I I I,对其在 x x x方向应用Sobel算子,可以得到一个新的图像 G x G_x Gx,其中每个像素的值表示其在 x x x方向上的梯度大小,即
G x ( i , j ) = ∑ m = − 1 1 ∑ n = − 1 1 H x ( m + 2 , n + 2 ) I ( i + m , j + n ) G_{x}(i, j)=\sum_{m=-1}^{1} \sum_{n=-1}^{1} H_{x}(m+2, n+2) I(i+m, j+n) Gx(i,j)=m=−1∑1n=−1∑1Hx(m+2,n+2)I(i+m,j+n)
类似地,对图像 I I I在 y y y方向应用Sobel算子,可以得到一个新的图像 G y G_y Gy,其中每个像素的值表示其在 y y y方向上的梯度大小,即
G y ( i , j ) = ∑ m = − 1 1 ∑ n = − 1 1 H y ( m + 2 , n + 2 ) I ( i + m , j + n ) G_{y}(i, j)=\sum_{m=-1}^{1} \sum_{n=-1}^{1} H_{y}(m+2, n+2) I(i+m, j+n) Gy(i,j)=m=−1∑1n=−1∑1Hy(m+2,n+2)I(i+m,j+n)
最终的梯度图像 G G G可以通过 G x G_x Gx和 G y G_y Gy的平方和再开方得到
G ( i , j ) = G x ( i , j ) 2 + G y ( i , j ) 2 G(i,j)=\sqrt{ G_{x}(i,j)^{2}+G_{y}(i,j)^{2} } G(i,j)=Gx(i,j)2+Gy(i,j)2
Sobel算子的目的是找到图像中灰度变化剧烈的位置,也就是边缘。通过比较每个像素点的梯度大小和方向,可以将图像中的边缘部分提取出来,方便后续的图像分析和处理
B:示例
如下图为一计算示例

C:程序

matlab实现:
Image=im2double(rgb2gray(imread('lotus.jpg')));
figure,imshow(Image),title('原图像');
BW= edge(Image,'sobel');
figure,imshow(BW),title('边缘检测');
H1=[-1 -2 -1;0 0 0;1 2 1];
H2=[-1 0 1;-2 0 2;-1 0 1];
R1=imfilter(Image,H1);
R2=imfilter(Image,H2);
edgeImage=abs(R1)+abs(R2);
figure,imshow(edgeImage),title('Sobel梯度图像');
sharpImage=Image+edgeImage;
figure,imshow(sharpImage),title('Sobel锐化图像');Python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt# 读入图像并转换为灰度图
image = cv2.imread('lotus.jpg')
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
image_gray = cv2.normalize(image_gray.astype('float'), None, 0.0, 1.0, cv2.NORM_MINMAX)# 显示原图像
plt.imshow(image_gray, cmap='gray')
plt.title('原图像')
plt.show()# 边缘检测
edge_image = cv2.Sobel(image_gray, cv2.CV_64F, 1, 0) + cv2.Sobel(image_gray, cv2.CV_64F, 0, 1)
edge_image = cv2.normalize(np.abs(edge_image), None, 0.0, 1.0, cv2.NORM_MINMAX)# 显示边缘检测结果
plt.imshow(edge_image, cmap='gray')
plt.title('边缘检测')
plt.show()# Sobel梯度图像
H1 = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
H2 = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
R1 = cv2.filter2D(image_gray, -1, H1)
R2 = cv2.filter2D(image_gray, -1, H2)
sobel_image = np.abs(R1) + np.abs(R2)
sobel_image = cv2.normalize(sobel_image, None, 0.0, 1.0, cv2.NORM_MINMAX)# 显示Sobel梯度图像
plt.imshow(sobel_image, cmap='gray')
plt.title('Sobel梯度图像')
plt.show()# Sobel锐化图像
sharp_image = image_gray + sobel_image
sharp_image = cv2.normalize(sharp_image, None, 0.0, 1.0, cv2.NORM_MINMAX)# 显示Sobel锐化图像
plt.imshow(sharp_image, cmap='gray')
plt.title('Sobel锐化图像')
plt.show()(4)Prewitt算子
A:定义
Prewitt算子:是一种经典的图像边缘检测算子,用于检测图像中的水平和垂直边缘。它是一种离散型微分算子,通过对图像像素值的梯度计算来提取边缘信息。对于一个灰度图像 I I I,Prewitt算子分别对图像的水平和垂直方向计算梯度,得到两个梯度图像 G x G_x Gx 和 G y G_y Gy。这些梯度图像的元素值表示在每个像素处的梯度大小和方向。Prewitt算子的水平和垂直模板分别为
H x = [ − 1 0 1 − 1 0 1 − 1 0 1 ] 和 H y = [ − 1 − 1 − 1 − 0 0 0 1 1 1 ] H_{x}=\begin{bmatrix} -1 & 0 & 1\\ -1 & 0 & 1\\ -1 & 0 & 1 \end{bmatrix}和H_{y}=\begin{bmatrix} -1 & -1 & -1\\ -0 & 0 & 0\\ 1 & 1 & 1 \end{bmatrix} Hx= −1−1−1000111 和Hy= −1−01−101−101
水平和垂直梯度图像的计算公式为:
*表示卷积运算
G x = I ∗ H x , G y = I ∗ H y G_{x}=I*H_{x},G_{y}=I*H_{y} Gx=I∗Hx,Gy=I∗Hy
最后,可以将水平和垂直梯度图像结合起来计算边缘梯度图像 G G G:
G = G x 2 + G y 2 G=\sqrt{ G^{2}_{x}+G^{2}_{y} } G=Gx2+Gy2
根据梯度大小和方向的信息,可以通过设置一个阈值来判断像素是否为边缘,从而提取出图像中的边缘信息
B:示例

C:程序

matlab实现:
clear,clc,close all;
Image=im2double(rgb2gray(imread('lotus.jpg')));
H1=[-1 -1 -1;0 0 0;1 1 1];
H2=[0 -1 -1;1 0 -1; 1 1 0];
H3=[1 0 -1;1 0 -1;1 0 -1];
H4=[1 1 0;1 0 -1;0 -1 -1];
H5=[1 1 1;0 0 0;-1 -1 -1];
H6=[0 1 1;-1 0 1;-1 -1 0];
H7=[-1 0 1;-1 0 1;-1 0 1];
H8=[-1 -1 0;-1 0 1;0 1 1];
R1=imfilter(Image,H1);
R2=imfilter(Image,H2);
R3=imfilter(Image,H3);
R4=imfilter(Image,H4);
R5=imfilter(Image,H5);
R6=imfilter(Image,H6);
R7=imfilter(Image,H7);
R8=imfilter(Image,H8);
edgeImage1=abs(R1)+abs(R7);
sharpImage1=edgeImage1+Image;
f1=max(max(R1,R2),max(R3,R4));
f2=max(max(R5,R6),max(R7,R8));
edgeImage2=max(f1,f2);
sharpImage2=edgeImage2+Image;
subplot(221),imshow(edgeImage1),title('两个模板边缘检测');
subplot(222),imshow(edgeImage2),title('八个模板边缘检测');
subplot(223),imshow(sharpImage1),title('两个模板边缘锐化');
subplot(224),imshow(sharpImage2),title('八个模板边缘锐化');Python实现:
import cv2
import matplotlib.pyplot as plt
import numpy as np# 读取图像并转换为灰度图像
image = cv2.imread('lotus.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
image = np.float32(image) / 255# 定义边缘检测和边缘锐化的卷积核
H1 = np.array([[-1, -1, -1], [0, 0, 0], [1, 1, 1]])
H2 = np.array([[0, -1, -1], [1, 0, -1], [1, 1, 0]])
H3 = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]])
H4 = np.array([[1, 1, 0], [1, 0, -1], [0, -1, -1]])
H5 = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]])
H6 = np.array([[0, 1, 1], [-1, 0, 1], [-1, -1, 0]])
H7 = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]])
H8 = np.array([[-1, -1, 0], [-1, 0, 1], [0, 1, 1]])# 对图像进行卷积操作,得到八个卷积结果
R1 = cv2.filter2D(image, -1, H1)
R2 = cv2.filter2D(image, -1, H2)
R3 = cv2.filter2D(image, -1, H3)
R4 = cv2.filter2D(image, -1, H4)
R5 = cv2.filter2D(image, -1, H5)
R6 = cv2.filter2D(image, -1, H6)
R7 = cv2.filter2D(image, -1, H7)
R8 = cv2.filter2D(image, -1, H8)# 计算两个模板和八个模板的边缘检测结果和边缘锐化结果
edgeImage1 = np.abs(R1) + np.abs(R7)
sharpImage1 = edgeImage1 + image
f1 = np.maximum(np.maximum(R1, R2), np.maximum(R3, R4))
f2 = np.maximum(np.maximum(R5, R6), np.maximum(R7, R8))
edgeImage2 = np.maximum(f1, f2)
sharpImage2 = edgeImage2 + image# 显示图像
plt.subplot(221), plt.imshow(edgeImage1, cmap='gray'), plt.title('两个模板边缘检测')
plt.subplot(222), plt.imshow(edgeImage2, cmap='gray'), plt.title('八个模板边缘检测')
plt.subplot(223), plt.imshow(sharpImage1, cmap='gray'), plt.title('两个模板边缘锐化')
plt.subplot(224), plt.imshow(sharpImage2, cmap='gray',plt.title('八个模板边缘锐化')三:二阶微分算子
(1)定义
二阶微分算子(拉普拉斯算子):在三维欧几里得空间中,拉普拉斯算子通常表示为 Δ \Delta Δ,它可以被定义为向量算子 ∇ \nabla ∇ 的散度的运算,即
Δ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \Delta^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} Δ2f=∂x2∂2f+∂y2∂2f
其中
∂ 2 f ∂ x 2 = Δ x f ( x + 1 , y ) − Δ x f ( x , y ) = [ f ( x + 1 , y ) − f ( x , y ) ] − [ f ( x , y ) − f ( x − 1 , y ) ] = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) ∂ 2 f ∂ y 2 = Δ y f ( x , y + 1 ) − Δ y f ( x , y ) = [ f ( x , y + 1 ) − f ( x , y ) ] − [ f ( x , y ) − f ( x , y − 1 ) ] = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \begin{aligned}\frac{\partial^{2} f}{\partial x^{2}} & =\Delta_{x} f(x+1, y)-\Delta_{x} f(x, y) \\& =[f(x+1, y)-f(x, y)]-[f(x, y)-f(x-1, y)] \\& =f(x+1, y)+f(x-1, y)-2 f(x, y) \\\frac{\partial^{2} f}{\partial y^{2}} & =\Delta_{y} f(x, y+1)-\Delta_{y} f(x, y) \\& =[f(x, y+1)-f(x, y)]-[f(x, y)-f(x, y-1)] \\& =f(x, y+1)+f(x, y-1)-2 f(x, y)\end{aligned} ∂x2∂2f∂y2∂2f=Δxf(x+1,y)−Δxf(x,y)=[f(x+1,y)−f(x,y)]−[f(x,y)−f(x−1,y)]=f(x+1,y)+f(x−1,y)−2f(x,y)=Δyf(x,y+1)−Δyf(x,y)=[f(x,y+1)−f(x,y)]−[f(x,y)−f(x,y−1)]=f(x,y+1)+f(x,y−1)−2f(x,y)
(2)示例
如下图为示例

(3)程序

matlab实现:
Image=im2double(rgb2gray(imread('lotus.jpg')));
figure,imshow(Image),title('原图像');
H=fspecial('laplacian',0);
R=imfilter(Image,H);
edgeImage=abs(R);
figure,imshow(edgeImage),title('Laplacian梯度图像');
H1=[0 -1 0;-1 5 -1;0 -1 0];
sharpImage=imfilter(Image,H1);
figure,imshow(sharpImage),title('Laplacian锐化图像');
Python实现:
import cv2
import matplotlib.pyplot as pltImage = cv2.imread('lotus.jpg')
Image = cv2.cvtColor(Image, cv2.COLOR_BGR2GRAY)
Image = cv2.normalize(Image.astype('float'), None, 0.0, 1.0, cv2.NORM_MINMAX)plt.imshow(Image, cmap='gray')
plt.title('原图像')
plt.show()H = cv2.Laplacian(Image, ddepth=-1, ksize=3)
R = cv2.filter2D(Image, -1, H)edgeImage = cv2.convertScaleAbs(R)plt.imshow(edgeImage, cmap='gray')
plt.title('Laplacian梯度图像')
plt.show()H1 = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]])
sharpImage = cv2.filter2D(Image, -1, H1)plt.imshow(sharpImage, cmap='gray')
plt.title('Laplacian锐化图像')
plt.show()相关文章:

(数字图像处理MATLAB+Python)第七章图像锐化-第一、二节:图像锐化概述和微分算子
文章目录 一:图像边缘分析二:一阶微分算子(1)梯度算子A:定义B:边缘检测C:示例D:程序 (2)Robert算子A:定义B:示例C:程序 &a…...

C# | 内存池
内存池 文章目录 内存池前言什么是内存池内存池的优点内存池的缺点 实现思路示例代码结束语 前言 在上一篇文章中,我们介绍了对象池的概念和实现方式。对象池通过重复利用对象,避免了频繁地创建和销毁对象,提高了系统的性能和稳定性。 今天我…...

程序设计入门——C语言2023年5月10日
程序设计入门——C语言 1、window下安装gcc 课程来源:链接: 浙江大学 翁恺 程序设计入门——C语言 学习日期:2023年5月10日 1、window下安装gcc 如果想让gcc在windows下运行,需要将gcc,及对于的lib包,都安装到window…...

【2023华为OD笔试必会25题--C语言版】《03 单入口空闲区域》——递归、数组、DFS
本专栏收录了华为OD 2022 Q4和2023Q1笔试题目,100分类别中的出现频率最高(至少出现100次)的25道,每篇文章包括原始题目 和 我亲自编写并在Visual Studio中运行成功的C语言代码。 仅供参考、启发使用,切不可照搬、照抄,查重倒是可以过,但后面的技术面试还是会暴露的。✨✨…...
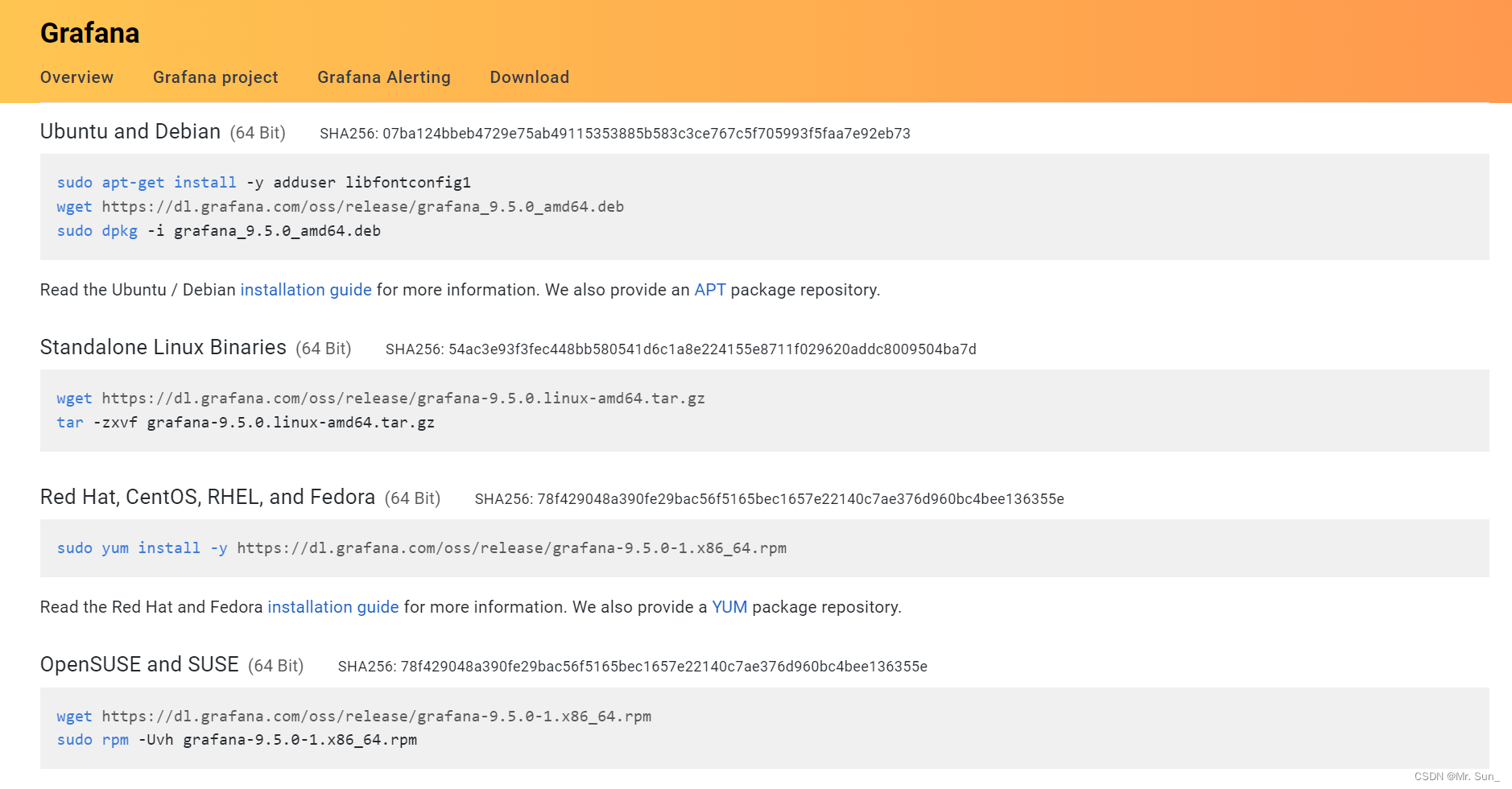
Grafana安装、升级与备份(02)
一、安装Grafana软件包 Grafana部署非常简单,直接使用yum命令从官网拉到安装再启动就可以了,本次使用的grafana版本为9.5.0 官网下载地址:Download Grafana | Grafana Labs # wget yum install -y https://dl.grafana.com/oss/release/grafana-9.5.0-1.x86_64.rpm # yum …...

【2023华为OD笔试必会25题--C语言版】《10 相同数字的积木游戏》——数组
本专栏收录了华为OD 2022 Q4和2023Q1笔试题目,100分类别中的出现频率最高(至少出现100次)的25道,每篇文章包括原始题目 和 我亲自编写并在Visual Studio中运行成功的C语言代码。 仅供参考、启发使用,切不可照搬、照抄,查重倒是可以过,但后面的技术面试还是会暴露的。✨✨…...

awk命令编辑
awk工作原理 逐行读取文本,默认以空格或tab键分隔符进行分隔,将分隔所得的各个字段保存到内建变量中,并按模式或者条件执行编辑命令。 sed命令常用于一整行的处理,而awk比较倾向于将一行分成多个“字段”然后再进行处理。awk信息…...

Pinia和Vuex的区别
Pinia和Vuex都是Vue.js状态管理库 Pinia是一个轻量级的状态管理库,它专注于提供一个简单的API来管理应用程序的状态。 相比之下,Vuex是一个更完整的状态管理库,它提供了更多的功能,比如模块化、插件和严格模式等。 Pinia是基于V…...

《C++高并发服务器笔记——第四章Linux网络编程》
计算机网络等相关知识可以去小林coding进行巩固(点击前往) 《C高并发服务器笔记——第四章》 4.1、网络结构模式1.C/S结构①C/S结构简介②C/S结构优点③C/S结构缺点 2.B/S结构①B/S结构简介②B/S结构优点③B/S结构缺点 4.2和4.3、MAC地址、IP地址、端口…...
NFS服务器搭建(案例)
目录标题 第一个问题1.安装软件包2.进入配置文件进行定义,并创建对应的资源文件3.客户端进行挂载,并查看挂载信息,修改挂载权限4.客户端查看挂载的信息 第二个问题1.服务端配置文件进行定义,并创建对应资源文件2.客户端进行挂载3.…...

ubuntu 22.04 安装 Docker Desktop 及docker介绍
目录 一、Docker Desktop 安装 1、我们先去官网下载安装包 2、Install Docker Desktop on Ubuntu 3、Launch Docker Desktop 二、Docker 介绍 什么是docker 如何使用docker docker是如何工作的 docker build docker run docker pull 一、Docker Desktop 安装 1、我们先…...

微前端中的应用隔离是什么,一般是怎么实现的?
微前端中的应用隔离是什么,一般是怎么实现的? 前言一、iframe 隔离二、Web Components三、JavaScript 沙箱隔离四、Shadow DOM 隔离总结 前言 微前端中的应用隔离是指将不同的微前端应用程序隔离开来,以确保它们之间不会相互影响或干扰。这种隔离可以通…...

【python pandas】合并文件并剔除重复数据
1.背景 工作中需要处理多个文件,每个文件里面有重复的数据,剔除重复数据,保留最新的数据 2.代码: import pandas as pd import osdl [] #person_list是文件路径 for i in range(person_list_len):#把文件df全部集合进列表dldl.a…...

Spellman高压电源X射线发生器维修XRB160PN480X4593
spellman高压发生器维修VMX40P5X4629;Spellman X射线发生器维修X4593系列 X射线源维修。 Spellman所拥有的变频器架构可以使高压电源获得高利用率的效率和功率密度。固体密封的高压模块进一步减少了尺寸和重量。 基于表面贴装控制电路的数字信号处理器提供通讯接口…...
msvcr120.dll丢失怎样修复?msvcr120.dll丢失修复的四个方法
打开软件跟游戏提示msvcr120.dll丢失,无法执行此代码怎么办?刚刚遇到这个问题,我都无从下手。家人们,你是不是也被这个问题也困扰过。msvcr120.dll是什么文件呢?经过我一个下午的时间研究,终于搞清楚了&…...
马哈鱼SQLFLow数据流生成介绍
马哈鱼数据血缘分析器是当前最流行的数据血缘关系(data lineage)管理工具之一,它是一种通过分析SQL脚本来自动发现数据流向的工具。它通过生成一个简洁的图表来显示数据仓库中表/视图和列之间的数据流。支持超过20种流行的数据库,包括 bigquery, couchba…...

使用 MVC 模式,实现简单登录功能 (Kotlin)
先放效果图: 第一张是登录页面效果图。用户输入登录名和密码,经过后台的非空验证和固定值验证,跳转到首页 第二张是首页效果图。用户点击 “update” 显示用户名和密码 这里的用户名和密码是后台设置的固定值,整体的登录逻辑特别…...
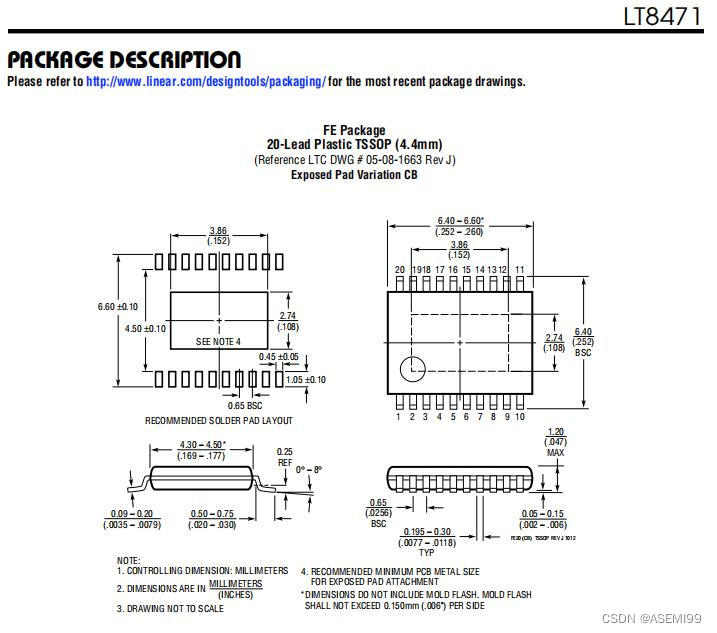
ASEMI代理LT8471IFE#PBF原装ADI车规级LT8471IFE#PBF
编辑:ll ASEMI代理LT8471IFE#PBF原装ADI车规级LT8471IFE#PBF 型号:LT8471IFE#PBF 品牌:ADI/亚德诺 封装:TSSOP-20 批号:2023 引脚数量:20 工作温度:-40C~125C 安装类型:表面…...
8. 100ASK_V853-PRO开发板支持MPP媒体处理平台
0.前言 MPP 系统控制模块,根据芯片特性,完成硬件各个部件的复位、基本初始化工作,同时负责完成 MPP(Media Process Platform 媒体处理平台)系统各个业务模块的初始化、去初始化以及管理 MPP 系统各个业务模块的工作…...

CLMP证书:让你在职场中脱颖而出的秘密武器!
CLMP证书是一种精益管理专业证书,是针对精益管理领域的专业人士和学生的培训项目,旨在提高他们在精益管理方面的技能和知识。那么,CLMP证书的含金量高吗?接下来我们来探讨一下。 CLMP证书的优势体现 首先,CLMP证书的…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
