【算法】Minimum Moves to Move a Box to Their Target Location 推箱子
文章目录
- Minimum Moves to Move a Box to Their Target Location 推箱子
- 问题描述:
- 分析
- 代码
- Tag
Minimum Moves to Move a Box to Their Target Location 推箱子
问题描述:
问题
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m x n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 ‘B’ 移动到目标位置 ‘T’ :
玩家用字符 ‘S’ 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
地板用字符 ‘.’ 表示,意味着可以自由行走。
墙用字符 ‘#’ 表示,意味着障碍物,不能通行。
箱子仅有一个,用字符 ‘B’ 表示。相应地,网格上有一个目标位置 ‘T’。
玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
玩家无法越过箱子。
返回将箱子推到目标位置的【最小 推动】 次数,如果无法做到,请返回 -1
地图是一个矩阵,MN,M,N的范围[1,20]
分析
对于人类来说,简单的关卡可以通过肉眼直接判断结果,但是对于复杂的关卡,仅依赖直观是无法判断的。这个游戏很多老的PDA上面都有。
这个游戏是推箱子,而不是拉箱子,所以箱子只能以一种方式移动。箱子最终的目的地一定是target坐标,或者永远无法抵达。
因为最终要求计算推动次数的最小值,而推动是以箱子移动为标准。
如果从其他坐标移动到坐标B,那么就会有4个方向,上下左右。所以对于human来说,也会有一个状态,之前是向上,为了使箱子移动到B,human的新坐标就是之前箱子的坐标。抽象的来说,箱子到达坐标B,一定会有4个状态,human也一样。
问题在于这个状态,如何表示和记录。
需要注意的是,human和box的关系,他们不一定是紧靠的,因为在需要换方向的时候,box不变,但是human的坐标是改变的。
即 box的坐标,human坐标,到达该box坐标的step,三者是有关系的。
而最终要算的是box从开始到达最终目的地坐标的最小移动。很明显是一个BFS。
定义一个队列queue,queue中存放的是 box坐标,human坐标组合表示的状态,然后利用数组记录到达该状态时的step,进行更新,就可以得到结果。
但是存在一个问题,BFS流程上会以第一次遇到目的地作为结束,返回结果,但是在这个问题上,出队的一个状态state,由它产生的状态可能是box不变,那么其state也不变,也可能是box移动了,那么其state就变了。如果统一的插入队尾,最终一定是出问题的。
可以使用2个queue来解决,当然也可以使用Deque。
对于一些无效的状态,肯定是不需要入队的。用dp[box] [human]记录状态box-human的最小移动,初始化dp 全部为 INTMAX。
如果dp[boxnew] [humannew]<=dp[boxpre] [humanpre]+1,说明这个new state已经visited。
当然对于boxnew来说,它要合法,不能越界,不能和墙重叠。
时间复杂度 O(M2N2)
空间复杂度: O(M2N2)
代码
class Solution {public int minPushBox(char[][] grid) {int m = grid.length, n = grid[0].length;int sx = -1, sy = -1, bx = -1, by = -1; // 玩家、箱子的初始位置for (int x = 0; x < m; x++) {for (int y = 0; y < n; y++) {if (grid[x][y] == 'S') {sx = x;sy = y;} else if (grid[x][y] == 'B') {bx = x;by = y;}}}int[] d = {0, -1, 0, 1, 0};int[][] dp = new int[m * n][m * n];for (int i = 0; i < m * n; i++) {Arrays.fill(dp[i], Integer.MAX_VALUE);}Queue<int[]> queue = new ArrayDeque<int[]>();dp[sx * n + sy][bx * n + by] = 0; // 初始状态的推动次数为 0queue.offer(new int[]{sx * n + sy, bx * n + by});while (!queue.isEmpty()) {Queue<int[]> queue1 = new ArrayDeque<int[]>();while (!queue.isEmpty()) {int[] arr = queue.poll();int s1 = arr[0], b1 = arr[1];int sx1 = s1 / n, sy1 = s1 % n, bx1 = b1 / n, by1 = b1 % n;if (grid[bx1][by1] == 'T') { // 箱子已被推到目标处return dp[s1][b1];}for (int i = 0; i < 4; i++) { // 玩家向四个方向移动到另一个状态int sx2 = sx1 + d[i], sy2 = sy1 + d[i + 1], s2 = sx2*n+sy2;if (!ok(grid, m, n, sx2, sy2)) { // 玩家位置不合法continue;}if (bx1 == sx2 && by1 == sy2) { // 推动箱子int bx2 = bx1 + d[i], by2 = by1 + d[i + 1], b2 = bx2*n+by2;if (!ok(grid, m, n, bx2, by2) || dp[s2][b2] <= dp[s1][b1] + 1) { // 箱子位置不合法 或 状态已访问continue;}dp[s2][b2] = dp[s1][b1] + 1;queue1.offer(new int[]{s2, b2});} else {if (dp[s2][b1] <= dp[s1][b1]) { // 状态已访问continue;}dp[s2][b1] = dp[s1][b1];queue.offer(new int[]{s2, b1});}}}queue = queue1;}return -1;}public boolean ok(char[][] grid, int m, int n, int x, int y) { // 不越界且不在墙上return x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != '#';}
}
代码来源于官解
Tag
BFS Dijkstra
相关文章:

【算法】Minimum Moves to Move a Box to Their Target Location 推箱子
文章目录 Minimum Moves to Move a Box to Their Target Location 推箱子问题描述:分析代码 Tag Minimum Moves to Move a Box to Their Target Location 推箱子 问题描述: 问题 「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓…...
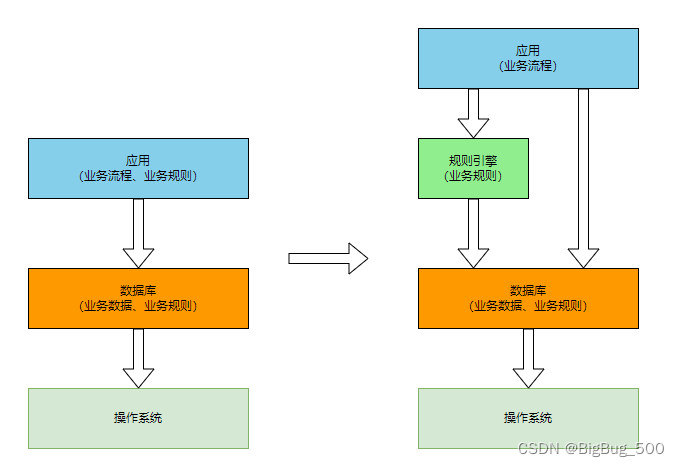
决策引擎平台建设方案
文档修订历史 时间版本主要内容2023.05.12v1.0.0初始化 1. 概述 1.1 需求 1.1.1 需求背景 当同一个业务场景中,有非常多的业务分支后,需要有非常多的 if 判断,来承载这些简单的业务逻辑,但随着业务的发展,业务逐渐…...
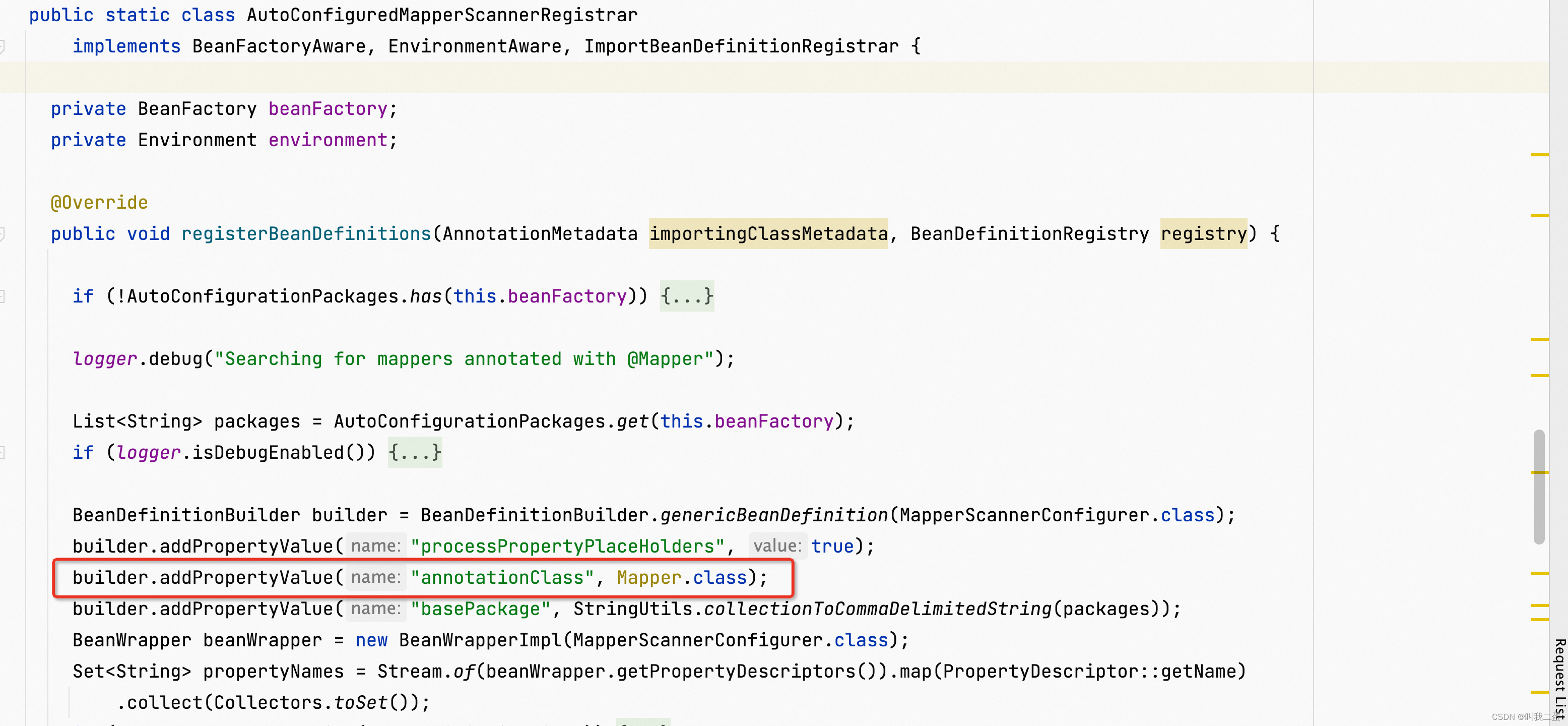
SpringBoot Starter 作用及原理
本文会以 mybatis 为例,通过对比 mybatis-spring 和 mybatis-spring-boot-starter 代码示例,了解 Starter 的作用。并对 mybatis-spring-boot-starter 进行简单剖析,了解 Starter 原理。 下面还有投票,一起参与进来吧👍…...

【rust】| 05——语法基础 | 流程控制
系列文章目录 【rust】| 00——开发环境搭建 【rust】| 01——编译并运行第一个rust程序 【rust】| 02——语法基础 | 变量(不可变?)和常量 【rust】| 03——语法基础 | 数据类型 【rust】| 04——语法基础 | 函数 【rust】| 05——语法基础 | 流程控制 文章目录 流程控制1. 条…...

解决Makefile: recipe for target ‘xxx‘ failed
author daisy.skye的博客_CSDN博客-嵌入式,Qt,Linux领域博主 问题 在android编译Kernel调用makefile引起的recipe for target 很多文章写的是由于编译文件路径引起或者是makefile代码中的空格引起的 分析 但是如果makefile文件不是手动配置的而且源代码提供的,…...

小黑子—多媒体技术与运用基础知识三:数字图形图像处理技术
多媒体技术与运用3.0 多媒体系列第三章1. 颜色科学1.1 颜色的性质1.1.1 颜色的物理性质1.1.2颜色三特性1.1.3三原色与三补色 1.2 颜色空间1.2.1 与设备无关的颜色空间1.2.1 与设备相关的颜色空间 1.3 常见的多媒体系统颜色空间1.3.1 RGB颜色空间1.3.2 CMYK颜色模型1.3.3 HSB颜色…...

Nginx实现ChatGPT API代理
文章目录 一、前言说明二、前置准备三、nginx配置三、代理域名用途 一、前言说明 本篇文章可以直接用于公司生产级的使用,所需要的资源直接改为公司级的即可平替使用文章均已通过实践应用,保证文章准确性,但因不同环境的不同可能效果不一致可…...

FileNotFoundError: [Errno 2] No such file or directory: ‘dot‘
FileNotFoundError: [Errno 2] No such file or directory: ‘dot’ 在绘制树形结构图的时候出现上述报错:已安装环境为ubuntu,python3.9 解决方案: 1、在终端输入sudo apt-get install graphviz,按回车键,输入密码&a…...

【分布族谱】正态分布和二项分布的关系
文章目录 正态分布二项分布验证 正态分布 正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性&am…...

7.设计模式之责任链模式
前言 责任链,即将能够处理同一类请求的对象连成一条链,所提交的请求沿着链传递, 链上的对象逐个判断是否有能力处理该请求,如果能则处理,如果不能则传递给链上的下一个对象。为了避免请求发送者与多个请求处理者耦合在…...

JAVA8的新特性——Stream
JAVA8的新特性——Stream 在这个深夜写下这篇笔记,窗外很安静,耳机里是《季节更替》,我感触还不是很多,当我选择封面图片的时候才发现我们已经渐渐远去,我们都已经奔赴生活,都在拼命想着去换一个活法&#…...

alias设置快捷键vim使用说明(解决服务器上输入长指令太麻烦的问题)
1. vi ~/.bashrc打开 2. (watch -n 1 gpustat 查看gpu使用情况 太麻烦)输入i进行编辑,最后一行输入 alias watchgpuwatch -n 1 gpustat alias gpuwatch -n 1 gpustat alias torch180source activate torch180 3. 按esc,然后输入:wq保存退出 4. source…...

英语基础句型之旅:从基础到高级
英语句型之旅:从基础到高级 一、起步:掌握英语基础句型 (Getting Started: Mastering Basic English Sentence Structures)1.1 英语句子的基本构成 (The Basic Components of English Sentences)1.2 五大基本句型解析 (Analysis of the Five Basic Sente…...
十四、Zuul网关
目录 一、API网关作用: 二、网关主要功能: 2.1、统一服务入口 2.2、接口鉴权 2.3、智能路由 2.4、API接口进行统一管理 2.5、限流保护 三、 新建一个项目作为网关服务器 3.1、项目中引入Zuul网关依赖 3.2、在项目application.yml中配置网关路由…...
5项目五:W1R3S-1(思路为主!)
特别注明:本文章只用于学习交流,不可用来从事违法犯罪活动,如使用者用来从事违法犯罪行为,一切与作者无关。 目录 前言 一、信息收集 二、网页信息的收集 三、提权 总结 前言 思路清晰: 1.信息收集,…...
Day958.代码的分层重构 -遗留系统现代化实战
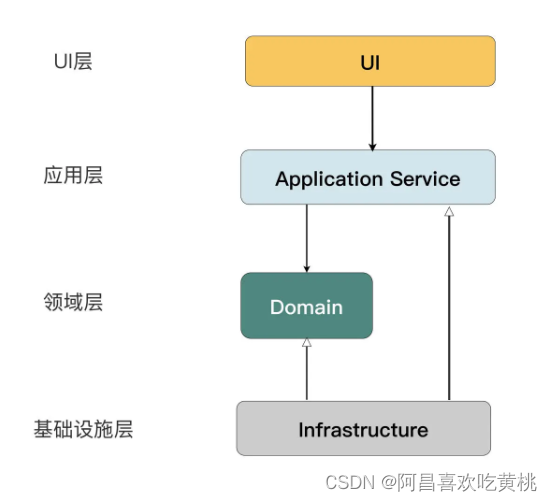
代码的分层重构 Hi,我是阿昌,今天学习记录的是关于代码的分层重构的内容。 来看看如何重构整体的代码,也就是如何对代码分层。 一、遗留系统中常见的模式 一个学校图书馆的借书系统。当时的做法十分“朴素”,在点击“借阅”按钮…...
分子模拟力场
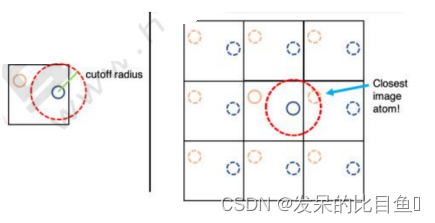
分子模拟力场 AMBER力场是在生物大分子的模拟计算领域有着广泛应用的一个分子力场。开发这个力场的是Peter Kollman课题组,最初AMBER力场是专门为了计算蛋白质和核酸体系而开发的,计算其力场参数的数据均来自实验值,后来随着AMBER力场的广泛…...

ERP 系统在集团化企业财务管理中的应用
(一)集团统一会计核算平台的构建原理及功能 第一,搭建集中统一会计核算平台的基础是确定财务组 织及岗位,在此基础上制定统一的会计核算政策、规范集中 基础数据、落实内控管理制度。 第二,具备了以上建立集中统一会计…...

达摩院开源多模态对话大模型mPLUG-Owl
miniGPT-4的热度至今未减,距离LLaVA的推出也不到半个月,而新的看图聊天模型已经问世了。今天要介绍的模型是一款类似于miniGPT-4和LLaVA的多模态对话生成模型,它的名字叫mPLUG-Owl。 论文链接:https://arxiv.org/abs/2304.14178…...

Group相关问题-组内节点限制移动范围
1.在节点中定义dragComputation,限制节点的移动范围 注意事项 组节点不定义go.Placeholder ,设置了占位符后组内节点移动将改变组节点位置dragComputation中自定义stayInGroup计算规则是根据groupNode的resizeObject计算 如果开启了resizable:true,建议指定其改变大的零部件r…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
