【分布族谱】正态分布和二项分布的关系
文章目录
- 正态分布
- 二项分布
- 验证
正态分布
正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性,使得正态分布拥有广泛的应用场景,或许正因如此,正太分布在分布族谱图中居于核心的位置。
正态分布 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)受到期望 μ \mu μ和方差 σ 2 \sigma^2 σ2的调控,其概率密度函数为
1 2 π σ 2 exp [ − ( x − μ ) 2 2 σ 2 ] \frac{1}{\sqrt{2\pi\sigma^2}}\exp[-\frac{(x-\mu)^2}{2\sigma^2}] 2πσ21exp[−2σ2(x−μ)2]
当 μ = 0 \mu=0 μ=0而 σ = 1 \sigma=1 σ=1时,为标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),对应概率分布函数为 Φ ( x ) = 1 2 π exp [ − x 2 2 ] \Phi(x)=\frac{1}{\sqrt{2\pi}}\exp[-\frac{x^2}{2}] Φ(x)=2π1exp[−2x2],形状如下,

在scipy.stats中,分别封装了正态分布类norm和标准正态分布类halfnorm。
二项分布
二项分布是非常简单而又基础的一种离散分布,貌似是高中学到的第一个分布,就算不是第一个,也是第一批。在 N N N次独立重复的伯努利试验中,设A在每次实验中发生的概率均为 p p p。则 N N N次试验后A发生 k k k次的概率分布,就是二项分布,记作 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p),则
P { X = k } = ( n k ) p k ( 1 − p ) n − k P\{X=k\}=\binom{n}{k}p^k(1-p)^{n-k} P{X=k}=(kn)pk(1−p)n−k
其中 ( n k ) = n ! k ! ( n − k ) ! \binom{n}{k}=\frac{n!}{k!(n-k)!} (kn)=k!(n−k)!n!,高中的写法一般是 C n k C^k_n Cnk。
记 q = 1 − p q=1-p q=1−p,令 x k = k − n p n p q x_k=\frac{k-np}{\sqrt{npq}} xk=npqk−np,当 n n n趋近于无穷大时,根据De Moivre–Laplace定理,有
lim n → ∞ n ! k ! ( n − k ) ! p k q n − k ≈ 1 2 π n p q e ( k − n p ) 2 2 n p q \lim_{n\to\infty}\frac{n!}{k!(n-k)!}p^kq^{n-k}\approx\frac{1}{\sqrt{2\pi npq}}e^{\frac{(k-np)^2}{2npq}} n→∞limk!(n−k)!n!pkqn−k≈2πnpq1e2npq(k−np)2
即服从 σ 2 = n p q , μ = n p \sigma^2=npq, \mu=np σ2=npq,μ=np的高斯分布。
验证
下面通过scipy.stats对二项分布和高斯分布之间的关联进行验证
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ssp,q = 0.2, 0.8
ns = [10, 100, 1000, 10000]fig = plt.figure()
for i,n in enumerate(ns):rs = ss.binom(n, p).rvs(50000)rv = ss.norm(n*p, np.sqrt(n*p*q))st, ed = rv.interval(0.999)xs = np.linspace(st, ed, 100)ys = rv.pdf(xs)ax = fig.add_subplot(2,2,i+1)ax.hist(rs, density=True, bins='auto', alpha=0.2)ax.plot(xs, ys)plt.title(f"n={n}")plt.show()
效果如下,可见随着 n n n越来越大,二项分布的随机数越来越靠近正态分布的概率密度曲线

相关文章:

【分布族谱】正态分布和二项分布的关系
文章目录 正态分布二项分布验证 正态分布 正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性&am…...

7.设计模式之责任链模式
前言 责任链,即将能够处理同一类请求的对象连成一条链,所提交的请求沿着链传递, 链上的对象逐个判断是否有能力处理该请求,如果能则处理,如果不能则传递给链上的下一个对象。为了避免请求发送者与多个请求处理者耦合在…...

JAVA8的新特性——Stream
JAVA8的新特性——Stream 在这个深夜写下这篇笔记,窗外很安静,耳机里是《季节更替》,我感触还不是很多,当我选择封面图片的时候才发现我们已经渐渐远去,我们都已经奔赴生活,都在拼命想着去换一个活法&#…...

alias设置快捷键vim使用说明(解决服务器上输入长指令太麻烦的问题)
1. vi ~/.bashrc打开 2. (watch -n 1 gpustat 查看gpu使用情况 太麻烦)输入i进行编辑,最后一行输入 alias watchgpuwatch -n 1 gpustat alias gpuwatch -n 1 gpustat alias torch180source activate torch180 3. 按esc,然后输入:wq保存退出 4. source…...

英语基础句型之旅:从基础到高级
英语句型之旅:从基础到高级 一、起步:掌握英语基础句型 (Getting Started: Mastering Basic English Sentence Structures)1.1 英语句子的基本构成 (The Basic Components of English Sentences)1.2 五大基本句型解析 (Analysis of the Five Basic Sente…...
十四、Zuul网关
目录 一、API网关作用: 二、网关主要功能: 2.1、统一服务入口 2.2、接口鉴权 2.3、智能路由 2.4、API接口进行统一管理 2.5、限流保护 三、 新建一个项目作为网关服务器 3.1、项目中引入Zuul网关依赖 3.2、在项目application.yml中配置网关路由…...
5项目五:W1R3S-1(思路为主!)
特别注明:本文章只用于学习交流,不可用来从事违法犯罪活动,如使用者用来从事违法犯罪行为,一切与作者无关。 目录 前言 一、信息收集 二、网页信息的收集 三、提权 总结 前言 思路清晰: 1.信息收集,…...
Day958.代码的分层重构 -遗留系统现代化实战
代码的分层重构 Hi,我是阿昌,今天学习记录的是关于代码的分层重构的内容。 来看看如何重构整体的代码,也就是如何对代码分层。 一、遗留系统中常见的模式 一个学校图书馆的借书系统。当时的做法十分“朴素”,在点击“借阅”按钮…...
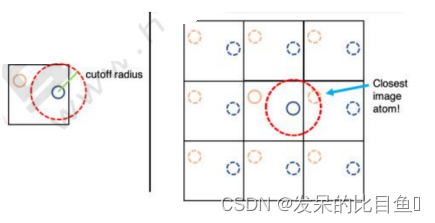
分子模拟力场
分子模拟力场 AMBER力场是在生物大分子的模拟计算领域有着广泛应用的一个分子力场。开发这个力场的是Peter Kollman课题组,最初AMBER力场是专门为了计算蛋白质和核酸体系而开发的,计算其力场参数的数据均来自实验值,后来随着AMBER力场的广泛…...

ERP 系统在集团化企业财务管理中的应用
(一)集团统一会计核算平台的构建原理及功能 第一,搭建集中统一会计核算平台的基础是确定财务组 织及岗位,在此基础上制定统一的会计核算政策、规范集中 基础数据、落实内控管理制度。 第二,具备了以上建立集中统一会计…...

达摩院开源多模态对话大模型mPLUG-Owl
miniGPT-4的热度至今未减,距离LLaVA的推出也不到半个月,而新的看图聊天模型已经问世了。今天要介绍的模型是一款类似于miniGPT-4和LLaVA的多模态对话生成模型,它的名字叫mPLUG-Owl。 论文链接:https://arxiv.org/abs/2304.14178…...

Group相关问题-组内节点限制移动范围
1.在节点中定义dragComputation,限制节点的移动范围 注意事项 组节点不定义go.Placeholder ,设置了占位符后组内节点移动将改变组节点位置dragComputation中自定义stayInGroup计算规则是根据groupNode的resizeObject计算 如果开启了resizable:true,建议指定其改变大的零部件r…...

程序员该如何学习技术
程序员该如何学习技术 前言 学习是第一生产力,我从来都是这么认为的,人只有只有不断地学习才能意识到自己的缺点和不足,身为程序员,我更认为人们应当抱着终身学习的想法实践下去,这是我所一直践行且相信的。 高处不胜寒…...

springboot+vue交流互动系统(源码+文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的交流互动系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 💕💕作者:风歌&a…...

【2023华为OD笔试必会25题--C语言版】《01 预定酒店》——排序、二分查找
本专栏收录了华为OD 2022 Q4和2023Q1笔试题目,100分类别中的出现频率最高(至少出现100次)的25道,每篇文章包括原始题目 和 我亲自编写并在Visual Studio中运行成功的C语言代码。 仅供参考、启发使用,切不可照搬、照抄,查重倒是可以过,但后面的技术面试还是会暴露的。✨✨…...

C语言实现队列--数据结构
😶🌫️Take your time ! 😶🌫️ 💥个人主页:🔥🔥🔥大魔王🔥🔥🔥 💥代码仓库:🔥🔥魔…...

前端CSS经典面试题总结
前端CSS经典面试题总结 2.1 介绍一 下 CSS 的盒子模型?2.2 css 选择器优先级?2.3 垂直居中几种方式?2.4 简明说一下 CSS link 与 import 的区别和用法?2.5 rgba和opacity的透明效果有什么不同?2.6 display:none和visib…...
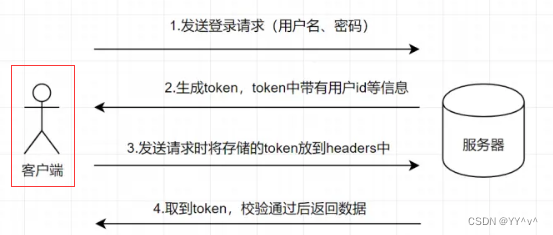
cookie、session、token的区别是什么
前言 今天就来说说session、cookie、token这三者之间的关系!最近这仨玩意搞得头有点大🤣 1.为什么会有它们三个? 我们都知道 HTTP 协议是无状态的,所谓的无状态就是客户端每次想要与服务端通信,都必须重新与服务端链接…...

leetcode分类刷题 -- 前缀和和哈希
力扣 class Solution { public int subarraySum(int[] nums, int k) { Map<Integer,Integer> map new HashMap<>(); int count0,sum0; map.put(0,1); for(int i:nums){ sum i; if(map.containsKey(sum-k)) count map.get(sum-k); map.compute(sum,(key,v)->…...

浅谈作为程序员如何写好文档:了解读者
我作为从一名懵懂的实习生转变为工程师的工作经历中,伴随着技术经验的成长,也逐渐意识到了编写文档是知识和经验传递给其他人的最有效方式。通过文档,可以分享我的技术知识和最佳实践,使其他人更好地理解我的工作。在这里…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
