剑指offer(C++)-JZ48:最长不含重复字符的子字符串(算法-动态规划)
作者:翟天保Steven
版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处

题目描述:
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
数据范围:
s.length≤40000 s.length≤40000
示例:
输入:
"abcabcbb"
返回值:
3
说明:
因为无重复字符的最长子串是"abc",所以其长度为 3。
解题思路:
本题是动态规划的经典题目。有两个解题思路。
思路一:滑动窗口
- 设计一个滑动窗口,窗口的右边界先行,用哈希表统计字符出现次数。
- 当出现重复字符时,左边界出发缩小窗口直到重复字符消失。
- 持续刷新最值就可以了。
思路二:动态规划
- 用哈希表存放字符上次出现的位置下标;用长度比字符串大1的vector,存放截止到第i个字符时,能继续维持的子串长度,比如v[0]=0,v[1]=1,v[2]可能为1可能为2。
- 执行遍历。用哈希表判断当前字符是否为重复字符,如果不是重复字符,那就在前面子串长度基础上加1;若出现了重复字符,则该字符与其重复字符的距离为i-m[s[i]],但如果两者之间有别的重复字符,则需要考虑此类情况,可以认为在其重复字符之后的子串中,该字符未出现过,则有v[i]+1;所以,比较v[i]+1和i-m[s[i]]谁小取谁,因为小的子串没断开,后续可以继续连接,而断开的子串虽然长度大,但不可以继续增加了。
- 持续更新字符最新下标以及子串长度最大值。
测试代码:
思路一:滑动窗口
class Solution {
public:// 最长子串int lengthOfLongestSubstring(string s) {// 定义哈希表unordered_map<char, int> m;// 滑动窗口遍历int result = 0;for(int left = 0, right = 0; right < s.length(); ++right){// 窗口右边界先行,统计字符出现次数m[s[right]]++;// 当出现重复字符,窗口左边界右移缩小窗口直到重复字符消失while(m[s[right]] > 1){m[s[left]]--;left++;}// 持续刷新子串最大长度result = max(result, right - left + 1);}return result;}
};思路二:动态规划
class Solution {
public:// 最长子串int lengthOfLongestSubstring(string s) {// 定义哈希表,存放的是字符出现的位置下标unordered_map<char, int> m;int result = 0;// v[i]表示截止到i个字符时,能继续维持的子串长度// 所以v[0]=0,v[1]=1vector<int> v = vector<int>(s.length() + 1, 0);// i是字符串中字符下标for(int i = 0; i < s.length(); ++i){// 当哈希表中没发现重复字符,那就在前面最长子串长度基础上+1if(m.find(s[i]) == m.end())v[i + 1] = v[i] + 1;// 若出现了重复字符,该字符与其重复字符的距离为i-m[s[i]]// 但如果两者之间有别的重复字符,那要考虑这类情况// 可以认为在其重复字符之后的子串中,该字符未出现过,则有v[i]+1// 所以v[i]+1和i-m[s[i]]谁小,取谁,因为小的这个子串没断开elsev[i + 1] = min(v[i] + 1, i - m[s[i]]);// 刷新该字符最新下标m[s[i]] = i;// 刷新最值result = max(result, v[i + 1]);}return result;}
};相关文章:

剑指offer(C++)-JZ48:最长不含重复字符的子字符串(算法-动态规划)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 题目描述: 请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。 数据范围…...

两阶段最小二乘法
两阶段最小二乘法 文章目录 两阶段最小二乘法[toc]1、ivreg包介绍2 、R语言实现 1、ivreg包介绍 R语言计量包ivreg用以解决线性回归模型的内生性问题。 描述:工具变量估计的线性模型通过两阶段最小二乘(2SLS) 回归或通过稳健回归M估计(2SM)或MM估计(2SMM)。主要的…...
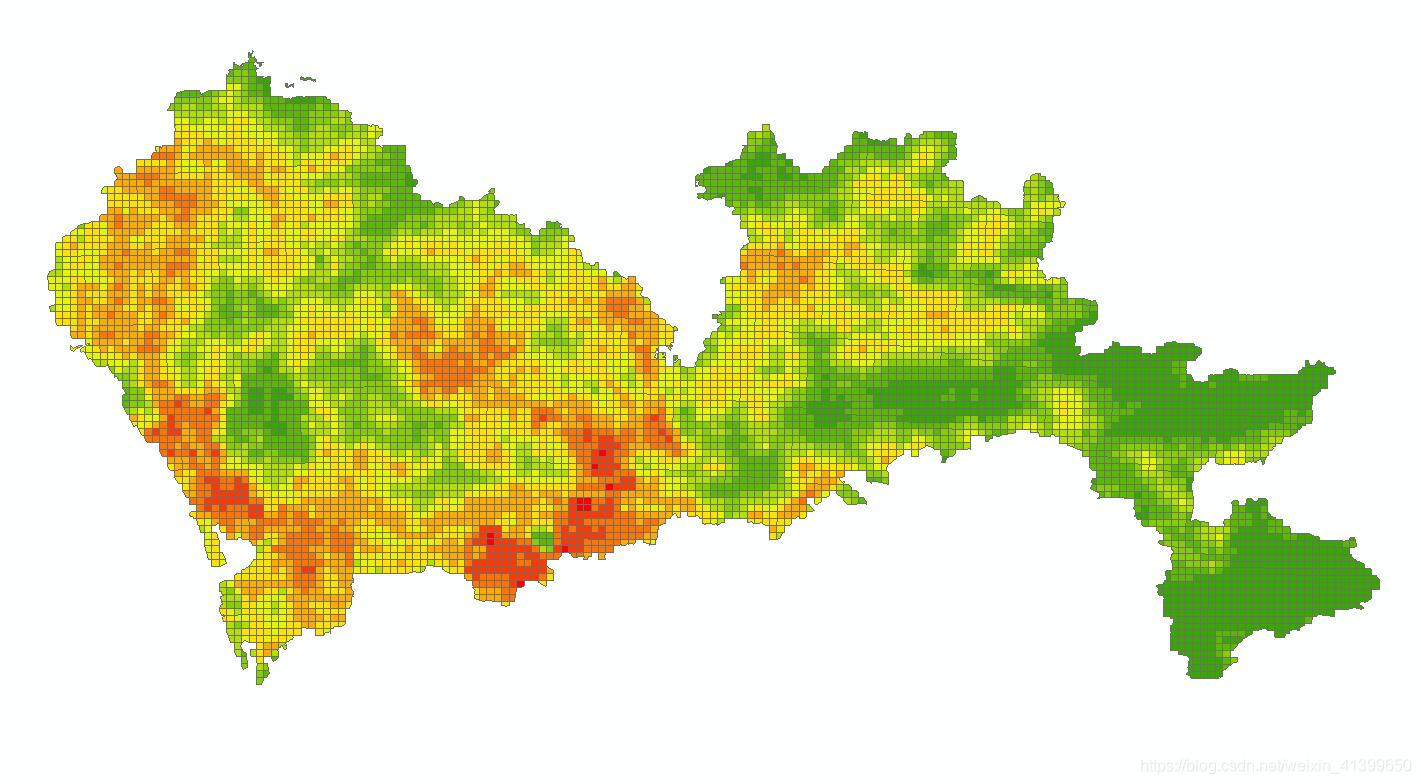
ArcMap创建格网统计图
目录 前言 一、人口数据获取 来源一:中科院地理所公开数据集 来源二:WorldPop数据集 二、人口格网统计步骤 1.创建渔网 2.人口数据处理 2.1 栅格转点 2.2 空间插值——处理人口缺失数据 2.3 空间连接——渔网人口统计 总结 前言 在科研中&am…...
[VAE] Auto-Encoding Variational Bayes
直接看paper看得云里雾里,李沐视频一语道破天机(建议从30min左右开始看GAN到Diffusion的串讲)。VAE的核心思路就是下面: 做生成,其实就是从随机向量(z)到目标图像(x)的过…...

《程序员面试金典(第6版)》面试题 16.19. 水域大小(深度优先搜索,类似棋盘类问题,八皇后的简化版本,C++)
题目描述 你有一个用于表示一片土地的整数矩阵land,该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小,返回值需要从小到…...
Spring 注解之@RestController与@Controller的区别
目录 1:介绍 2:区别 3:总体来说 4:社区地址 1:介绍 RestController 和 Controller 是 Spring MVC 中常用的两个注解,它们都可以用于定义一个控制器类。 2:区别 返回值类型不同:…...

Java中的泛型是什么?如何使用泛型
Java中的泛型是指在定义类、接口和方法时使用类型参数,以使得这些类、接口和方法可以操作多种类型的数据,从而提高代码的重用性和安全性。Java的泛型机制是从JDK5开始引入的,它使得Java程序员能够编写更加通用和类型安全的代码。 什么是泛型…...

【飞行棋】多人游戏-微信小程序开发流程详解
可曾记得小时候玩过的飞行棋游戏,是90后的都有玩过吧,现在重温一下,这是一个可以二到四个人参与的游戏,通过投骰子走棋,一开始靠运气,后面还靠自己选择,谁抢占先机才能赢,还可以和小…...

力扣 146. LRU 缓存
一、题目描述 请你设计并实现一个满足LRU(最近最少使用)缓存约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以正整数作为容量 capacity 初始化LRU缓存。int get(int key) 如果关键字 key 存在于缓存中,则返回关键…...

关于Oracle SCN的最大阈值
SCN每秒增长的速度跟Oracle的版本有关,在Oracle 11.2.0.2之前是每秒允许最大增长16384,在Oracle 11.2.0.2之后是默认每秒允许增长32768,这个值跟新增的隐含参数_max_reasonable_scn_rate有关,如下所示: NAME …...

Linux多路转接之poll
文章目录 一、poll的认识二、编写poll方案服务器三、poll方案多路转接的总结 一、poll的认识 多路转接技术是在不断更新进步的,一开始多路转接采用的是select方案,但是select方案存在的缺点比较多,所以在此基础上改进,产生了poll…...

Webpack打包流程
轻松了解Webpack 打包流程 Webpack是一个现代的JavaScript应用程序的静态模块打包器。它将多个JavaScript文件打包成一个或多个静态资源文件,以便在浏览器中加载。Webpack将应用程序视为一个依赖项图,其中包括应用程序的所有模块,然后通过该…...

React事件委托
React 事件委托(Event Delegation)是一种优化事件处理的技术,它通过将事件监听器添加到父级元素(而不是子元素)来实现。当事件触发时,事件会向上冒泡到父元素,然后在父元素上调用事件处理函数。…...
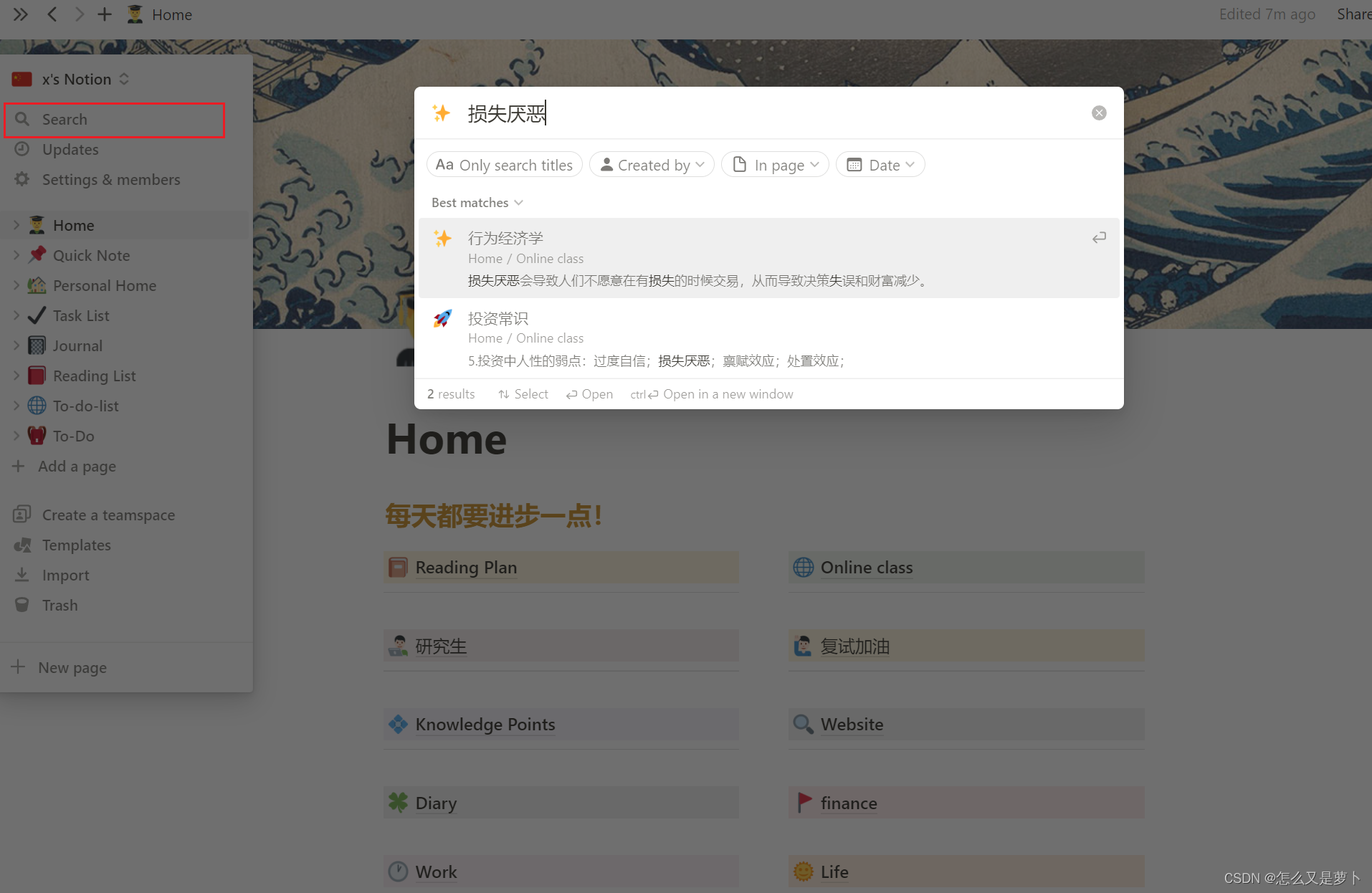
Notion——构建个人知识库
前言 使用Notion快三年了,它All in one的理念在使用以后确实深有体会,一直想找一个契机将这个软件分享给大家,这款笔记软件在网上已经有很多的教程了,所以在这里我主要想分享框架方面的内容给大家,特别对于学生党、研究…...

ModuleNotFoundError: No module named ‘Multiscaledeformableattention‘
在实现DINO Detection方法时,我们可能会遇到以上问题。因为在DeformableAttention模块,为了加速,需要自己去编译这个模块。 如果你的环境变量中能够找到cuda路径,使用正确的torch版本和cuda版本的话,这个问题很容易解…...

【数据结构】链表(C语言实现)
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c语言系列专栏:c语言之路重点知识整合 &#x…...
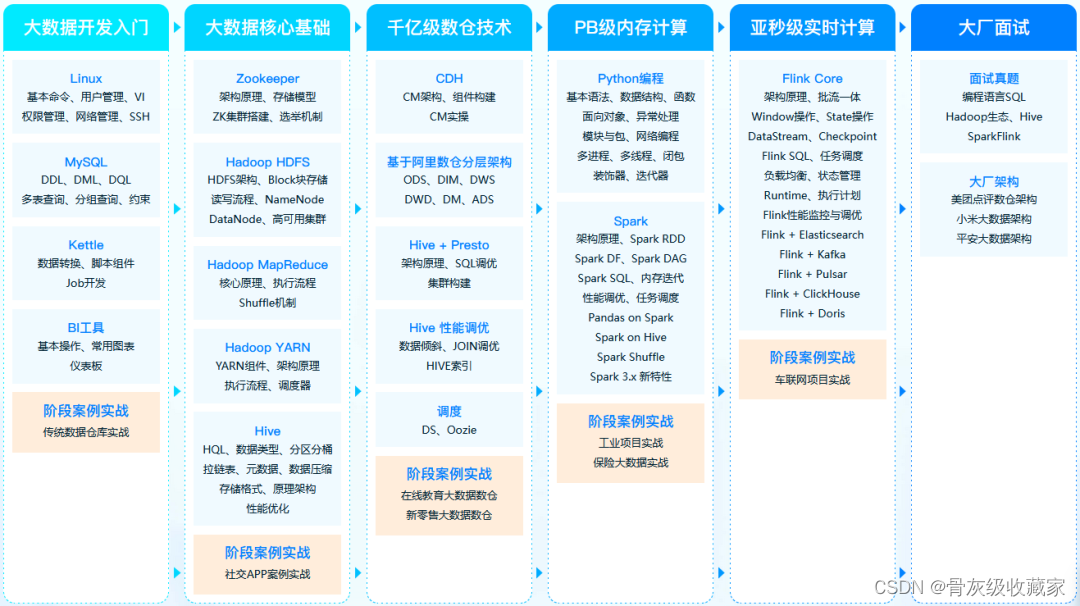
【2023程序员必看】大数据行业分析
1、政策重点扶持,市场前景广阔 2014年,大数据首次写入政府工作报告,大数据逐渐成为各级政府关注的热点。 2015年9月,国务院发布《促进大数据发展的行动纲要》,大数据正式上升至国家战略层面,十九大报告提…...
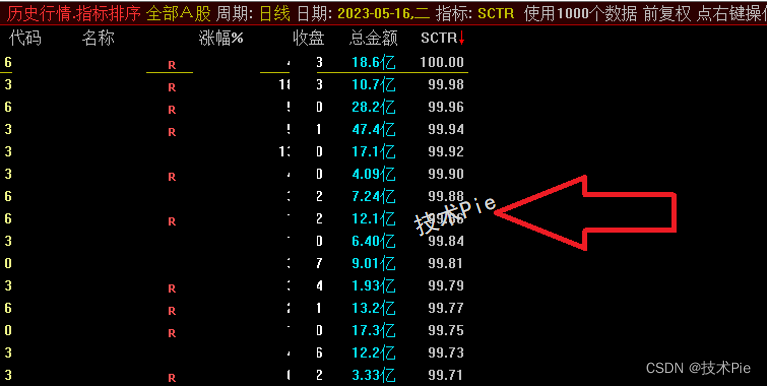
通达信SCTR强势股选股公式,根据六个技术指标打分
SCTR指标(StockCharts Technical Rank)的思路来源于著名技术分析师约翰墨菲,该指标根据长、中、短三个周期的六个关键技术指标对股票进行打分,根据得分对一组股票进行排名,从而可以识别出强势股。 与其他技术指标一样,SCTR的设计…...
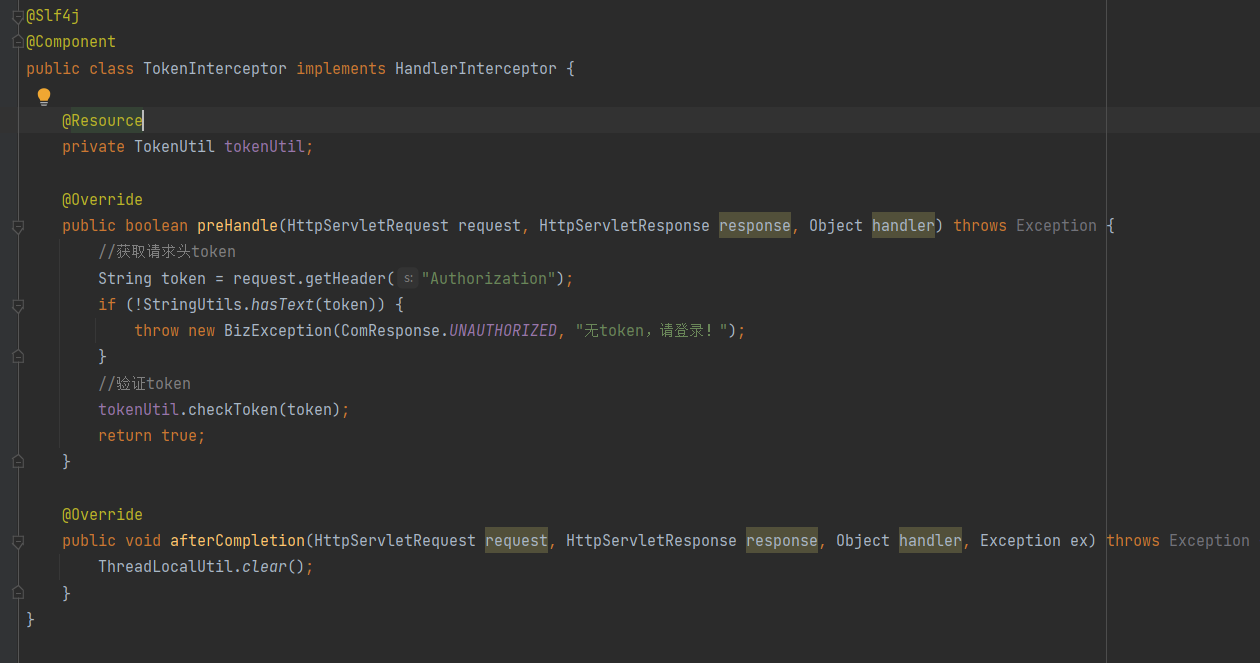
SpringBoot+Token+Redis+Lua+自动续签极简分布式锁Token登录方案
前言 用SpringBoot做一个项目,都要写登录注册之类的方案 使用Cookie或Session的话,它是有状态的,不符合现代的技术 使用Security或者Shiro框架实现起来比较复杂,一般项目无需用那么复杂 使用JWT它虽然是无状态的,也可…...
多模态:MiniGPT-4
多模态:MiniGPT-4 IntroductionMethodlimitation参考 Introduction GPT-4具有很好的多模态能力,但是不开源。大模型最近发展的也十分迅速,大模型的涌现能力可以很好的迁移到各类任务,于是作者猜想这种能力可不可以应用到多模态模…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
