素数相关(结合回文数,合数)线性筛素数(欧拉筛法)Euler【算法模板笔记】
一、朴素筛法(埃拉托斯特尼筛法)
Eratosthenes 筛法(埃拉托斯特尼筛法,简称埃氏筛法)
时间复杂度是O(nloglogn)
不常用,被欧拉筛代替,略
二、线性筛素数(欧拉筛法)
简介
线性筛法 也称为 Euler 筛法(欧拉筛法)
对比
普通的筛法就是1到n的倍数来筛,线性筛就是 用1到n中的素数的倍数来筛
时间复杂度 O(n)
buff
筛法求素数的同时也得到了每个数的最小质因子。
原理
中心思想:每个数只能被自己的最小质因子筛掉一次
算法原理解释
原理:对于任意合数,必定可以有最小质因子乘以最大因子的分解方式。因此,对于每个合数,只要用最大因子筛一遍,枚举时只要枚举最小质因子即可。由于每个合数都只被标记一次,达到了线性
// 任意合数,必定可以有最小质因子乘以最大因子的分解方式。
// 所以我们只要保证每个合数都由最小质因子筛掉就行了
//用两层循环枚举最小质因子和最大因子。i是最大因子,prime[j]是最小质因子
break整除中断原因
解释1
// 这里为什么要break
// 因为如果不break
// i * p[j + 1] 的最小质因子就不是p[j + 1] 了
// 而是 i 的最小质因子 p[j]。
解释2
//这个break发生时,这个primes[j]的值,是i的最小质因子
//保证合数只被最小质因子划掉一次
//如果i是质数,则最多枚举到自身中断
//如果i是合数,则最多枚举到自身的最小质数中断
文章
【算法/数论】欧拉筛法详解:过程详述、正确性证明、复杂度证明_CSDN博客_欧拉筛
例题
P3383 【模板】线性筛素数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
Sherlock and his girlfriend - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
三、与回文数结合
回文数
判断回文数
构造回文数
回文质数
偶数肯定不是质数。这样至少排除一半多的数据量
知识点: “偶数长度的回文数”中只有11是素数,其他的都可以被11整除。
偶数位数回文数(除11)必定不是质数
例题
回文素数 - 回文素数 - 力扣(LeetCode)
P1217 [USACO1.5]回文质数 Prime Palindromes - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
四、与合数结合
方法
用欧拉筛反向筛出合数
合数相关理论

例题
P1835 素数密度 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
模板
/*prime_nums_Euler*/
#include<bits/stdc++.h>
#define MAXN 100000005
using namespace std;//P3383 【模板】线性筛素数bool isprime[MAXN]; // isprime[i]表示i是不是素数
int prime[MAXN]; // 现在已经筛出的素数列表
int nums = 0; // 已经筛出的素数个数void euler_old(int n){memset(isprime, true, sizeof(isprime)); // 先全部标记为素数isprime[1] = false; // 1不是素数for(int i = 2; i <= n; ++i){ // i从2循环到n(外层循环)if(isprime[i]) prime[++nums] = i;// 如果i没有被前面的数筛掉,则i是素数for(int j = 1; j <= nums && prime[j] <= n/i; ++j){//枚举已经记录的质数(内层循环)//i * prime[j] <= n:由于题目只求小于n的数是否是质数,所以大于n的就不管了【越界中断】isprime[i * prime[j]] = false;// 倍数标记为合数,也就是i用prime[j]把i * prime[j]筛掉了if(i % prime[j] == 0) break;//【整除中断】}}
}//以下是acwing的模板int primes[MAXN], cnt; // primes[]存储所有素数
bool st[MAXN]; // st[x]存储x是否被筛掉:true表示要被筛掉(没有处理1的特判)void get_primes(int n){for(int i = 2; i <= n; i++){if(!st[i]) primes[cnt++] = i; //如果没有被筛掉,直接录入,并且cnt++for(int j = 0; primes[j] <= n/i; j++){ //从小到大枚举所有质数st[primes[j] * i] = 1; //筛掉质数的倍数的数if (i % primes[j] == 0) break; //【精髓:整除中断】//这个break发生时,这个primes[j]的值,是i的最小质因子}}
}int main(){int n; // 上限,即筛出<=n的素数scanf("%d", &n);get_primes(n);int q,k;//q次询问第 k 小的素数scanf("%d", &q);while(q--){scanf("%d", &k);printf("%d\n", primes[k-1]);}// for(int i = 2; i<=n; i++) if(isprime[i]) printf("%d ", i);// for(int i = 2; i<=n; i++) if(!st[i]) printf("%d ", i);return 0;
}相关文章:

素数相关(结合回文数,合数)线性筛素数(欧拉筛法)Euler【算法模板笔记】
一、朴素筛法(埃拉托斯特尼筛法)Eratosthenes 筛法(埃拉托斯特尼筛法,简称埃氏筛法)时间复杂度是O(nloglogn)不常用,被欧拉筛代替,略二、线性筛素数(欧拉筛法)简介线性筛…...
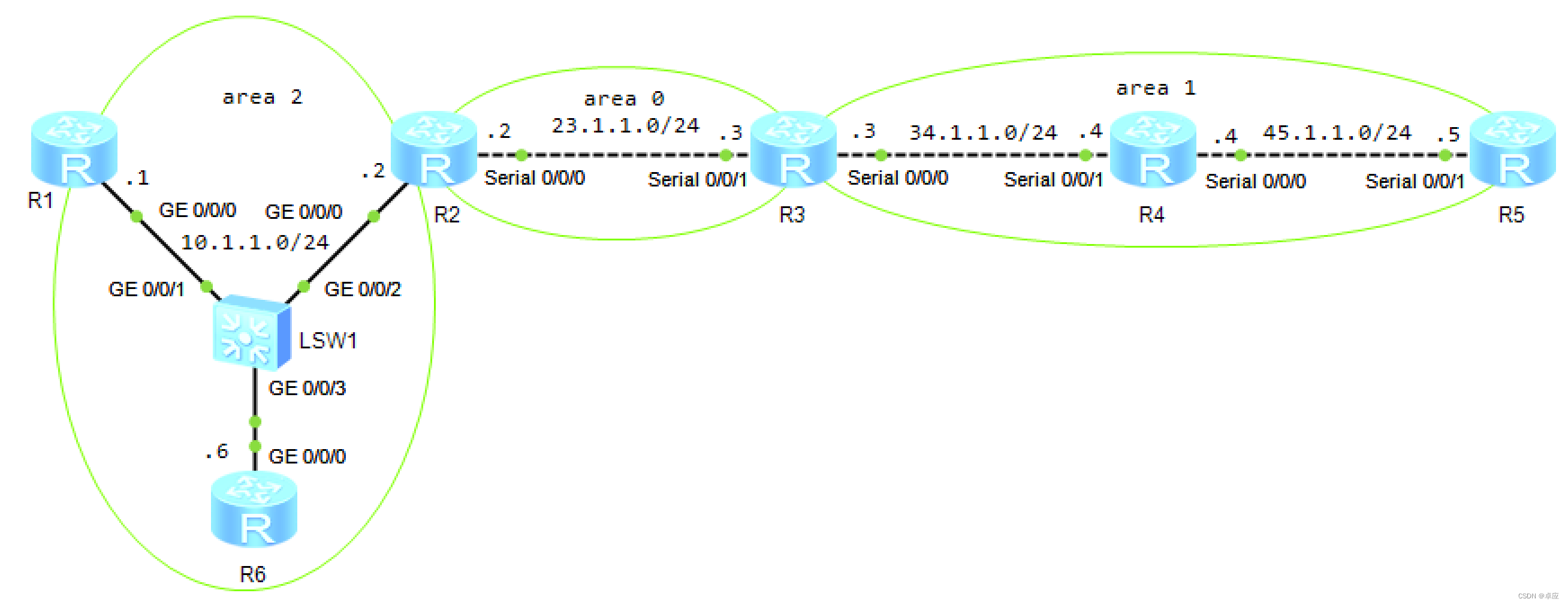
1.7配置OSPF手动汇总
实验7:配置OSPF手动汇总 实验目的实现OSPF路由汇总的配置阐明OSPF引入的外部路由时进行路由汇总的方法实验拓扑配置OSPF手动汇总实验拓扑如图1-17所示。 图1-17 配置OSPF手动汇总 实验步骤配置IP地址,配置OSPF(和实验6一致,此处略)在…...

多线程下载工具axel的安装和使用
多线程下载工具axel的安装和使用 Axel是一个轻量级下载程序,它和其他加速器一样,对同一个文件建立多个连接,每个连接下载单独的文件片段以更快地完成下载。 Axel 支持 HTTP、HTTPS、FTP 和 FTPS 协议。它也可以使用多个镜像站点下载单个文件…...

大数据专业职业前景如何
大数据专业毕业生未来的岗位选择空间比较大,有三大类岗位可选择分别是大数据开发岗位、大数据分析岗位和大数据运维岗位,在不同的行业和技术体系结构下这些岗位也包含很多细分的岗位。 大数据开发岗位分为平台研发岗位和行业场景开发岗位两大类…...

拉格朗日乘数法在原材料选择问题上的具体应用
问题需求: 输入待制作的材料:(材料长,材料数量) 分别为(5401,124)、(200,135)、(1350,45), 输入原材料长度最大值6500,最小值3500&…...
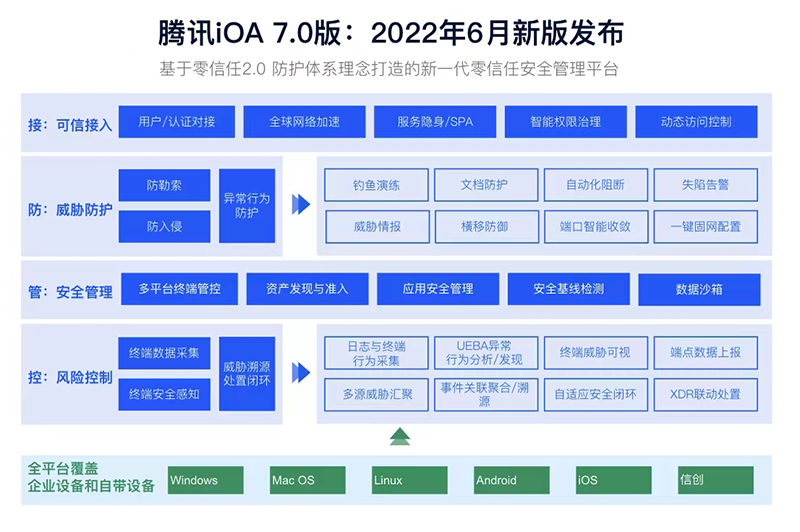
零信任-腾讯零信任iOA介绍(4)
腾讯零信任介绍 腾讯零信任是一种信息安全架构,旨在通过限制对计算设备、数据和应用程序的访问来保护敏感信息。腾讯零信任的主要思想是,任何计算设备、数据或应用程序都不应被自动信任,并需要经过授权后才能访问敏感信息。 腾讯零信任的…...

标准的maven依赖包应该包含哪些东西?
背景在阅读源码的时候,发现有一些maven依赖包里面没有包含pom文件,一些maven依赖包包含,而且除此之外还有一些细微的差异。今天就来聊一下关于一个标准的依赖包应该是什么样子的。一个标准的Maven依赖包通常包含以下文件:Java类文…...

网络安全-Nmap
网络安全-Nmap Nmap-号称诸神之眼 这个呢就是用来扫描网络端口的 Namp的工作原理很像一个雷达 做任何攻击之前,得先知道怎么去找破绽,而不是钢铁洪流,那个是不叫渗透了,叫硬钢。 咋用呢? 很简单 直接 nmap 后面跟网址…...
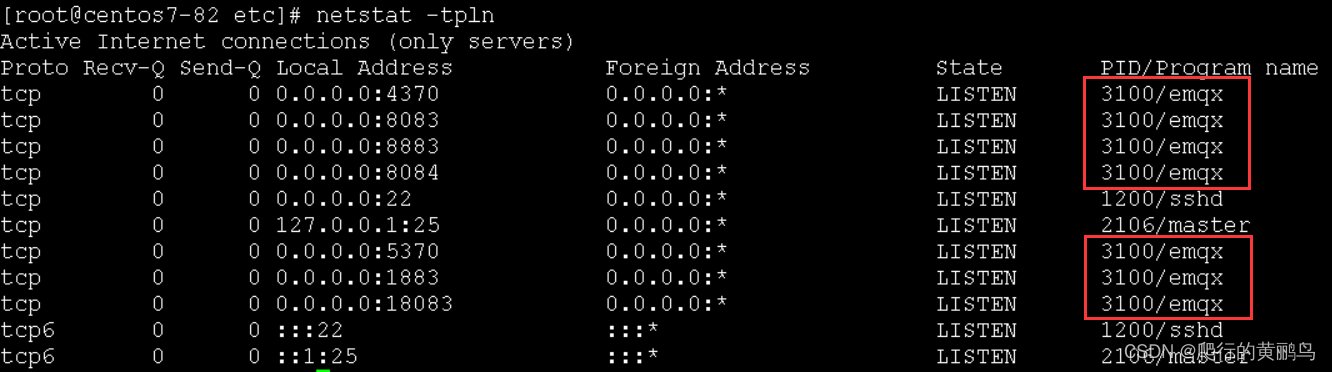
【物联网】mqtt初体验
文章目录安装EMQXjava集成添加依赖mqtt配置参数发布组件订阅组件测试接口接口测试最近在了解物联网云平台方面的知识,解除了mqtt协议,只看书籍难免有些枯燥,所以直接试验一下,便于巩固理论知识。 broker服务器操作系统:…...
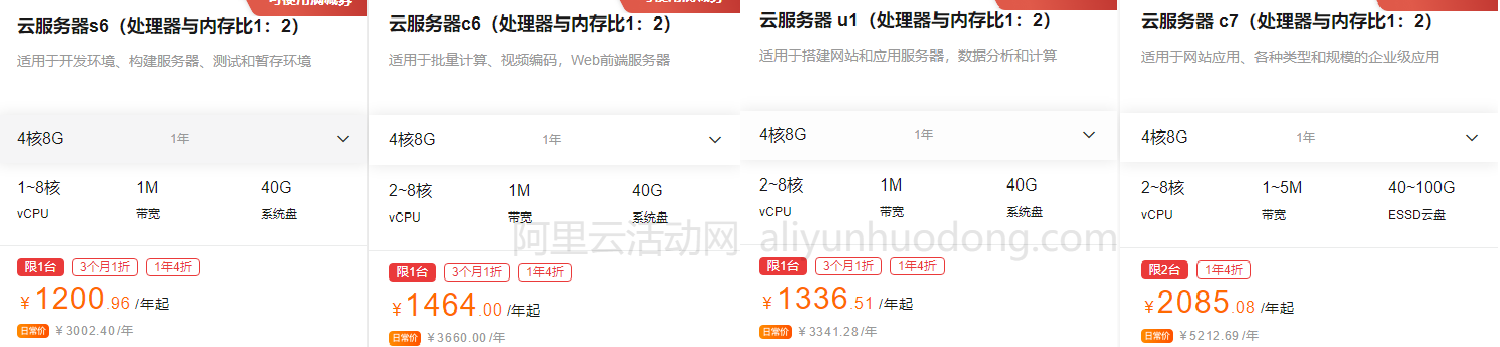
2023年阿里云活动有哪些实例规格的云服务器?如何选择这些实例规格
2023年阿里云活动有哪些实例规格的云服务器?新手用户通过阿里云活动选购阿里云服务器的时候实例规格应该怎么选,因为同配置的云服务器往往有多种不同是规格的云服务器可供选择,而且不同实例规格的云服务器之间价格差别还比较大,因…...
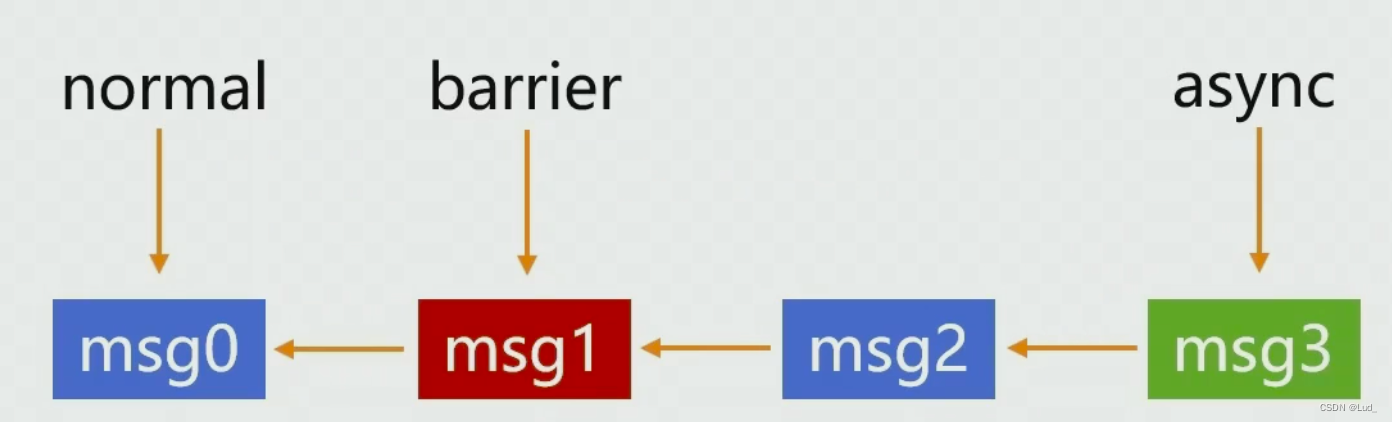
深入理解 Handler(java 层 + native 层)
文章目录回顾线程消息队列时怎样实现的消息是怎么传递的?Handle 的延迟消息是怎么处理的?IdleHandler 的原理主线程进入了 Looper 循环为什么没有 ANR?消息屏障是什么?回顾 之前学习过Handler相关的基础知识,今天再学…...
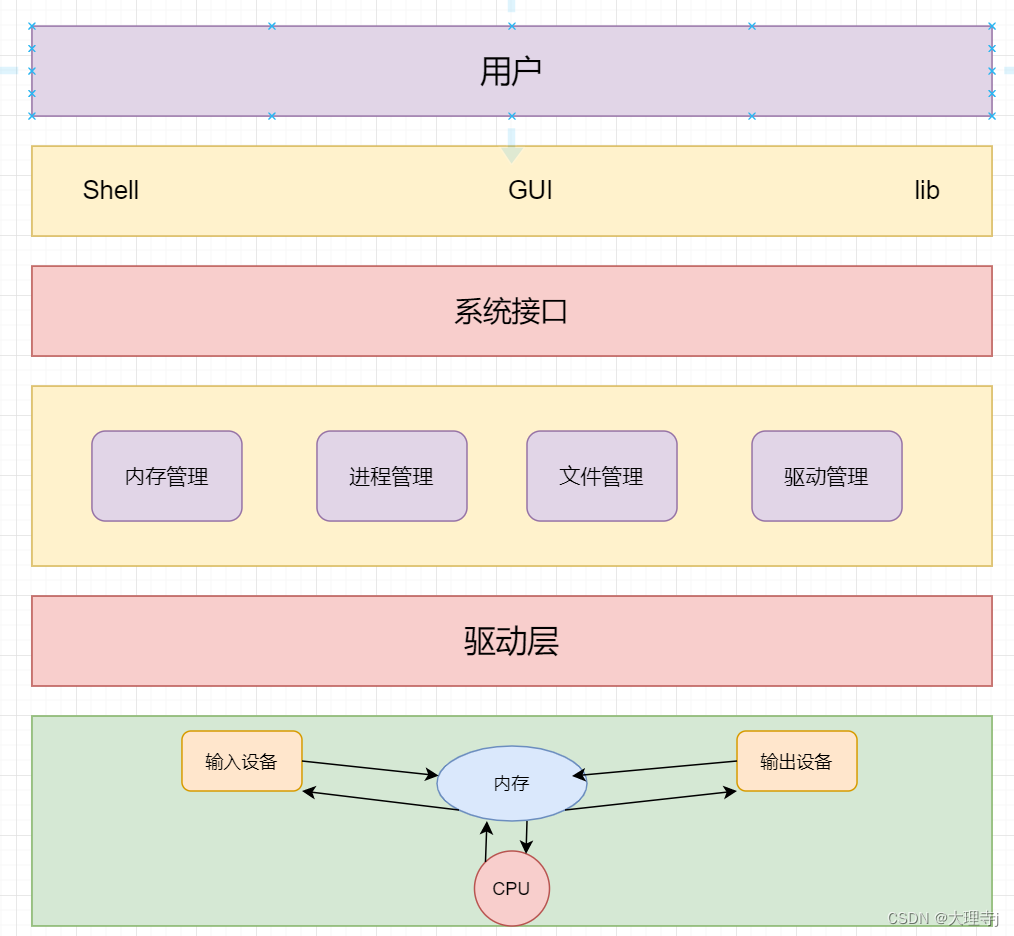
初步认识操作系统(Operator System)
操作系统一,冯诺依曼体系结构内存的重要作用二,操作系统的概念三,设计操作系统的目的三,操作系统在计算机体系中的定位四,操作系统是如何进行管理的一,冯诺依曼体系结构 在众多计算机相关的书籍中ÿ…...

Android—HTTPS部署自签名证书
一、生成自签名私有证书单向认证(只需要服务端证书) 生成server_ks.jks服务端密钥配置到服务端生成server.cer服务端证书配置到客户端 双向认证(还需要客户端证书,和信任证书) 生成client_ks.jks客户端密钥配置到客户…...
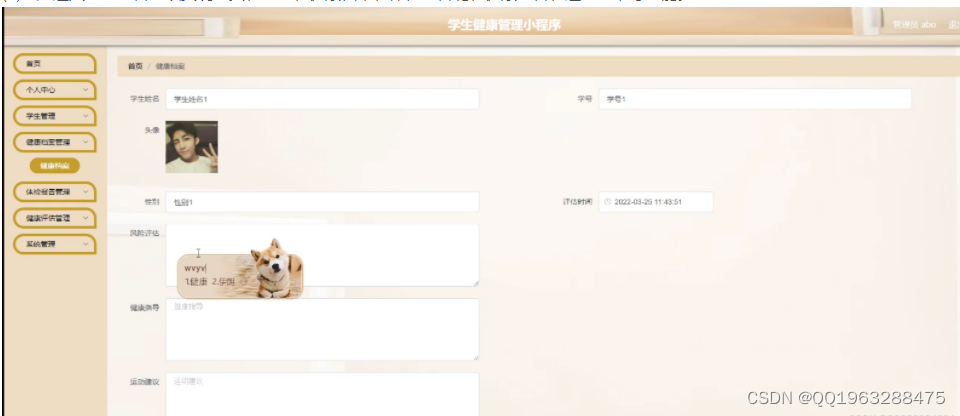
java基于springboot+vue微信小程序的学生健康管理
任何系统都要遵循系统设计的基本流程,本系统也不例外,同样需要经过市场调研,需求分析,概要设计,详细设计,编码,测试这些步骤,基于Java语言、微信小程序技术设计并实现了学生健康管理小程序。系统主要包括系统首页、个人中心、学生管理、健康档案管理、体检报告管理、健康评估管…...

金三银四丨黑蛋老师带你剖析-漏洞岗
作者丨黑蛋病毒岗之前我们简单看了看二进制逆向岗位和漏洞岗,今天我们来看一看病毒岗位,就单纯看二进制病毒岗位和漏洞岗位,其所需要的基础知识是差不多的,在Windows平台上,无非就是汇编,C语言,…...
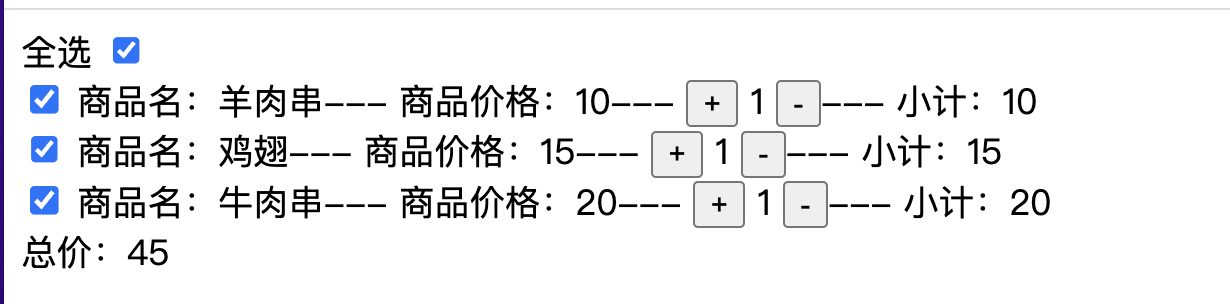
pinia实战 购物车(自定义插件实现pinia持久化)
目录 一、实例 二、需求 三. 代码解析 shop.vue shop.ts 四、持久化插件 插件介绍 持久化实现思路 一、实例 二、需求 单选全选功能,并且可以互相联动 小计功能 总计功能 商品加减,数量为零时不能在减 三. 代码解析 shop.vue 1.获取shop模块实…...
idea使用本地代码远程调试线上运行代码---linux环境
场景: 之前介绍过windows环境上,用idea进行远程调试那么在linux环境下实战一下 环境: linux 测试应用:使用docker部署的platform-multiappcenter-base-app-1.0.0-SNAPSHOT.jar 应用 测试应用端口:19001 测试工具&…...
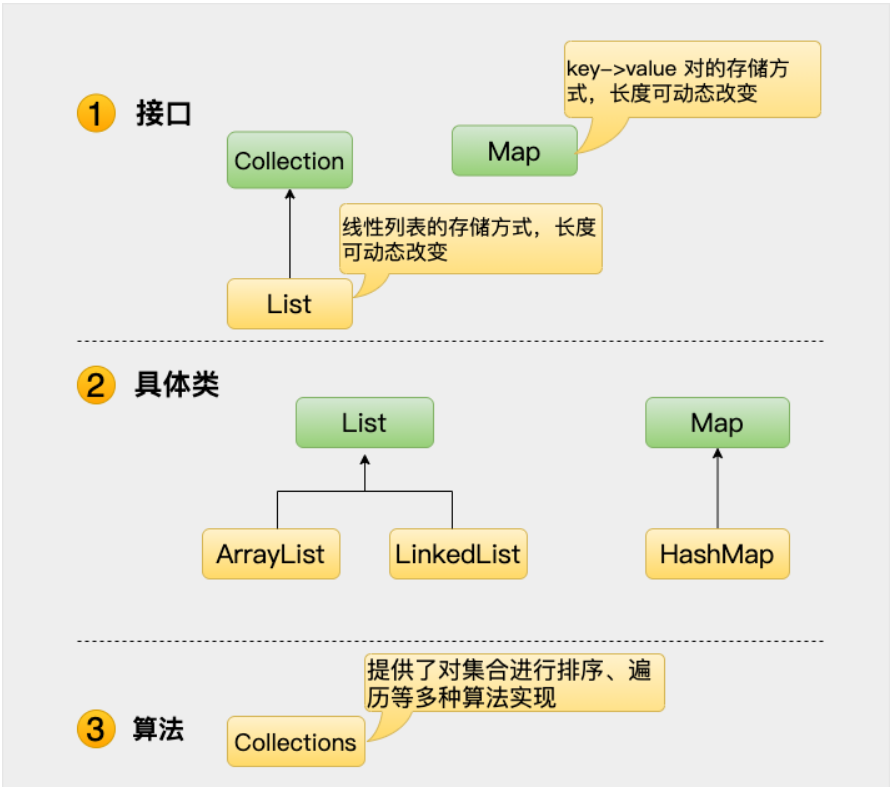
Java 基础面试题——集合
目录1.Java 有哪些常用容器(集合)?2.Collection 和 Collections 有什么区别?3.List、Set、Map 之间的区别是什么?4.HashMap 的长度为什么是 2 的 N 次方?源码中是如何保证的?5.HashMap 和 Hasht…...

编程思想、方法论和架构模式的应用
概要编程思想是指在编写代码时所采用的基本思维方式和方法论。分类编程思想分类:面向对象编程(Object-Oriented Programming,简称OOP):把数据和对数据的操作封装在一起,通过类和对象的概念实现模块化、可重…...
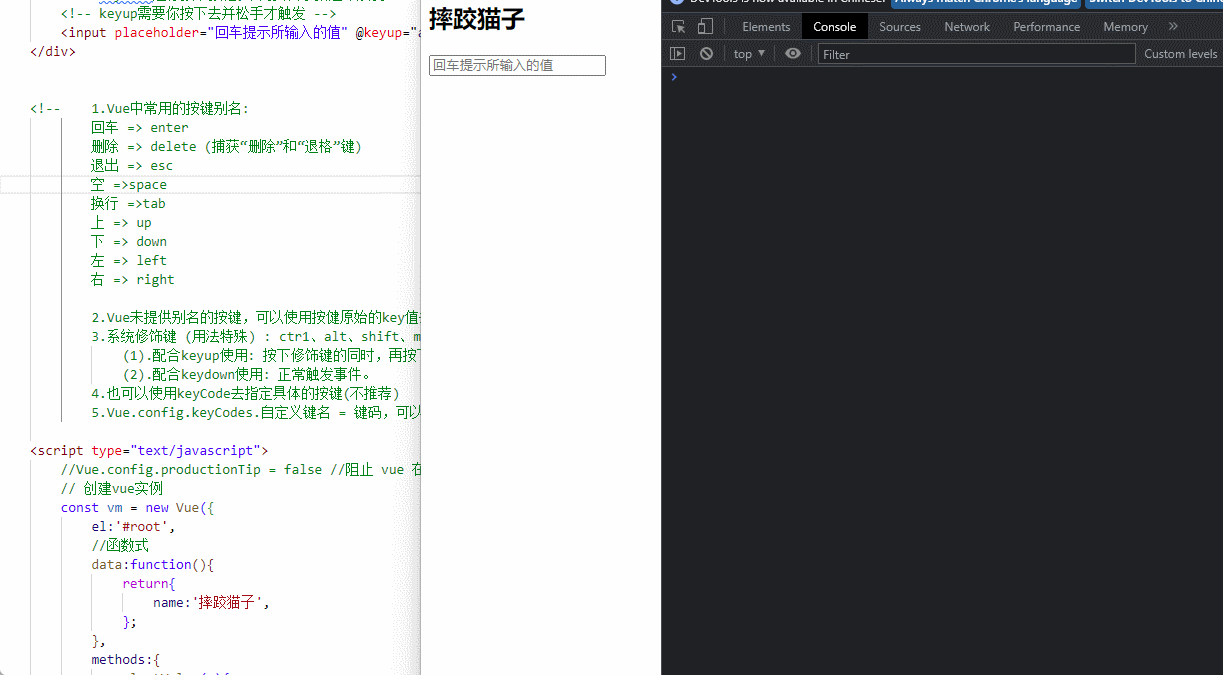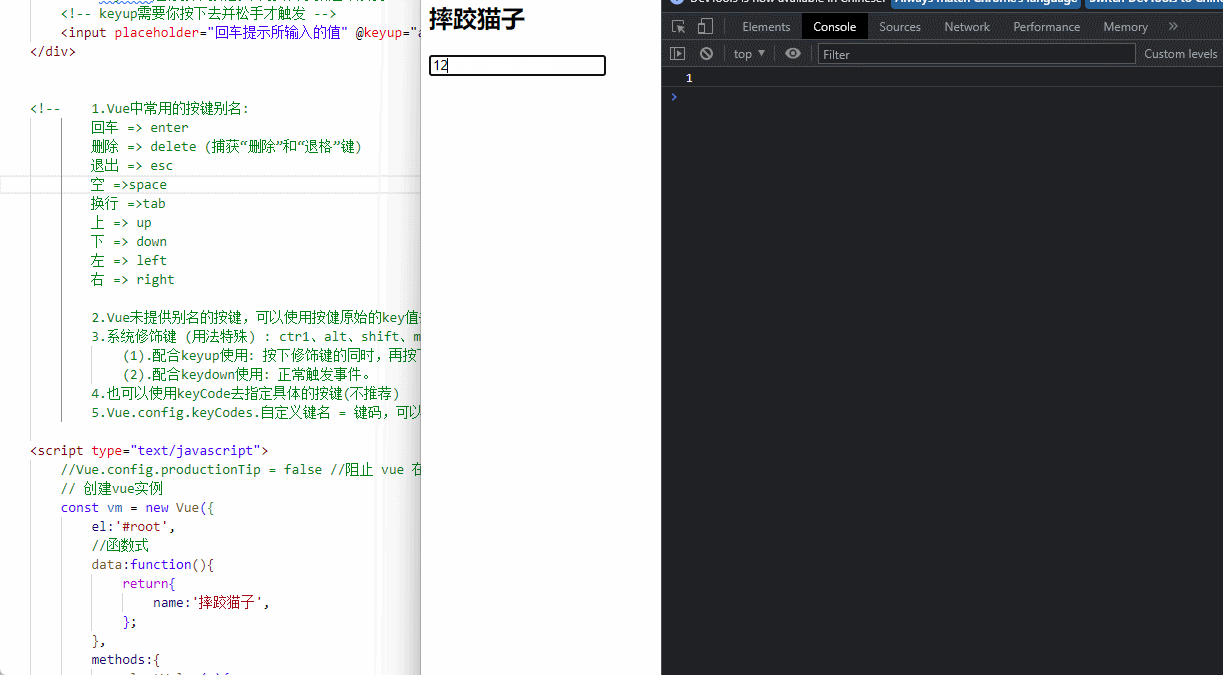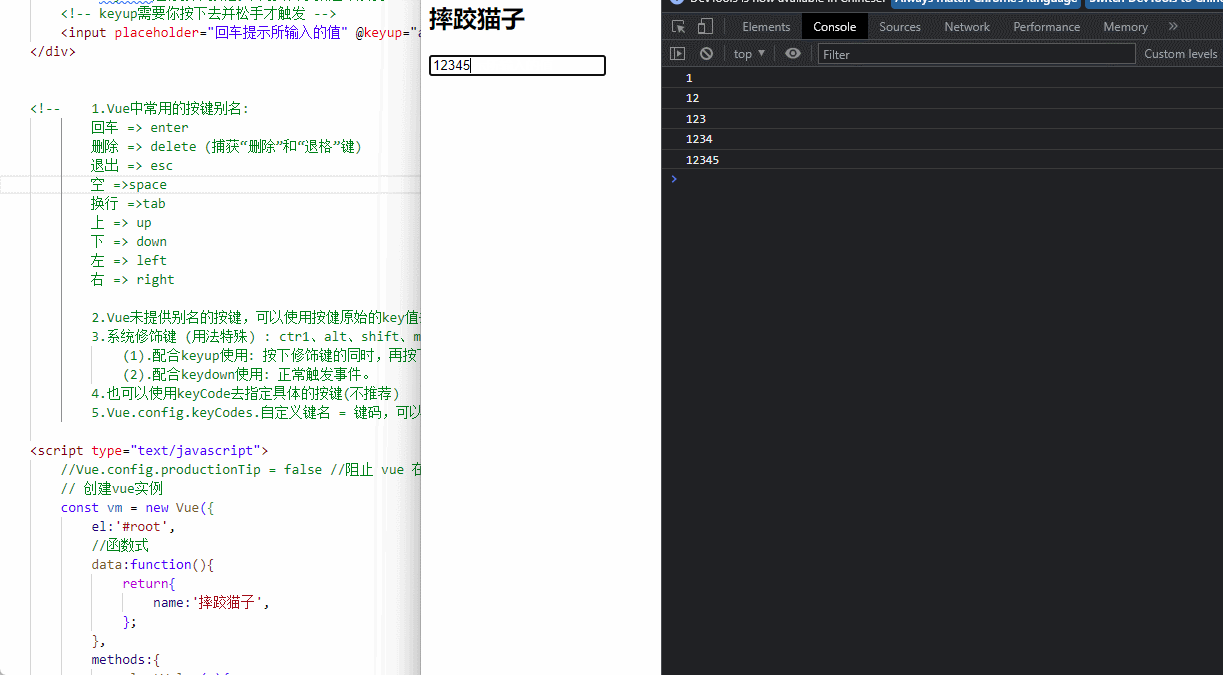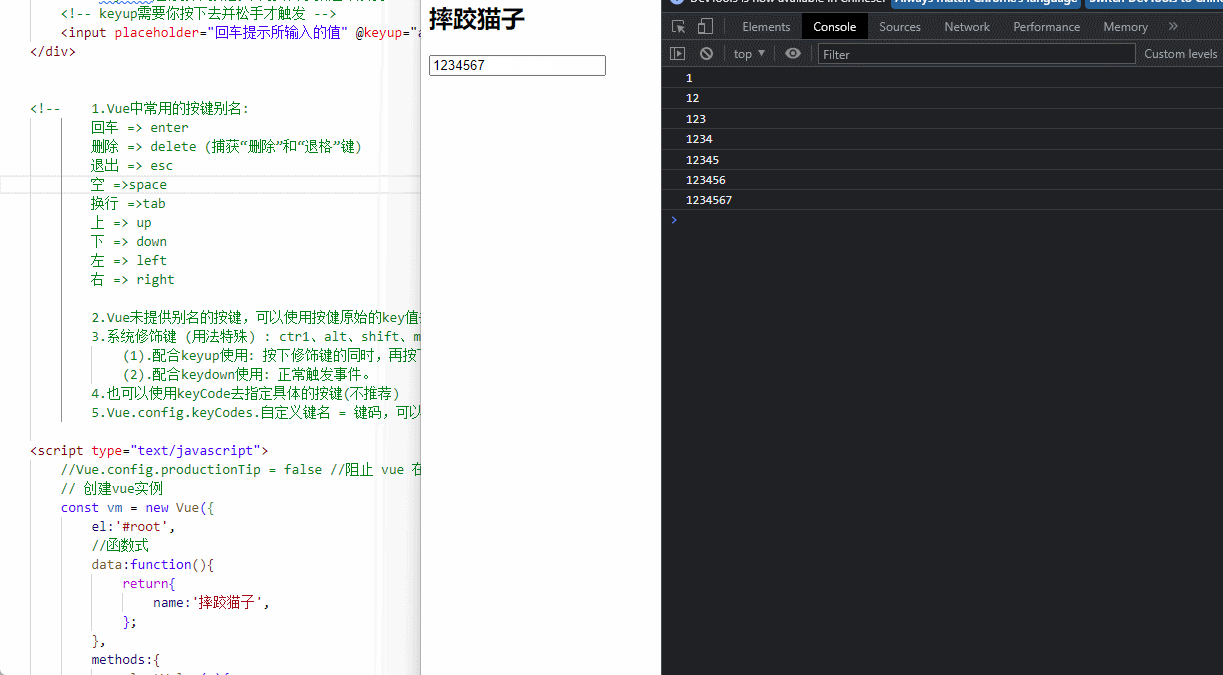
Vue|事件处理
事件处理1. 事件使用1.1 事件绑定1.2 事件参数2. 事件修饰符2.1 阻止默认事件2.2 阻止事件冒泡2.3 事件只允许触发一次2.4 事件捕获2.5 操作当前元素2.6 行为立即执行无需等待回调3. 键盘事件4. 本章小结4.1 事件使用小结4.2 事件修饰符小结4.3 键盘事件小结1. 事件使用 1.1 事…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
