用到的C++的相关知识-----未完待续
文章目录
- 前言
- 一、vector函数的使用
- 1.1 构造向量
- 二、常用函数
- 2.1 矩阵输出函数
- 2.2 向量输出函数
- 2.3 矩阵的使用
- 2.4
- 三、new的用法
- 3.1 内存的四种分区
- 3.2 new的作用
- 3.3
- 3.4
- 四、
- 4.1
- 4.2
- 4.3
- 4.4
- 总结
前言
只是为方便学习,不做其他用途
一、vector函数的使用
有关的文章
- C++ vector的用法(整理)
- C++中vector的用法详解
1.1 构造向量
//vector():创建一个空vectorvector<int> v1 = vector<int>(); //v1 = []//vector(int nSize):创建一个vector,元素个数为nSizevector<int> v2 = vector<int>(3); //v2 = [0, 0, 0]//vector(int nSize,const t& t): 创建一个vector,元素个数为nSize,且值均为tvector<int> v3 = vector<int>(3, 10); //v3 = [10, 10, 10]//vector(const vector&): 复制构造函数vector<int> v4 = vector<int>(v3); //v4 = [10, 10, 10]//vector(begin,end): 复制[begin,end)区间内另一个数组的元素到vector中vector<int> v5 = vector<int>(v4.begin(), v4.end() - 1); //v5 = [10, 10]vector<vector<int>> v6 = vector<vector<int>>(3, vector<int>(3);); //v6 = [[0, 0, 0][0, 0, 0][0, 0, 0]]二、常用函数
2.1 矩阵输出函数
// 输出矩阵的各个值
void Print(MatrixXd K)
{for (int j = 0; j < K.rows(); j++){for (int i = 0; i < K.cols(); i++){cout << K(j, i) << " ";}cout << endl;}
}
2.2 向量输出函数
#include <vector>
// 输出向量的各个值
void Print_Vector(vector<double> U)
{for (int i = 0; i < U.size(); i++){cout << " U_ " << i << " = " << U[i] << endl;}
}
2.3 矩阵的使用
eigen库和matlab中对应命令
// A simple quickref for Eigen. Add anything that's missing.
// Main author: Keir Mierle
#include<iostream>
#include <gismo.h>
#include <Eigen/Dense>
using namespace Eigen;
using namespace gismo;
using namespace std;
#include <vector>int main()
{gsMatrix<double, 3, 3> A; // Fixed rows and cols. Same as Matrix3d.Matrix<double, 3, Dynamic> B; // Fixed rows, dynamic cols.Matrix<double, Dynamic, Dynamic> C; // Full dynamic. Same as MatrixXd.Matrix<double, 3, 3, RowMajor> E; // Row major; default is column-major.Matrix3f P, Q, R; // 3x3 float matrix.Vector3f x, y, z; // 3x1 float matrix.RowVector3f a, b, c; // 1x3 float matrix.VectorXd v; // Dynamic column vector of doublesdouble s;// Basic usage// Eigen // Matlab // commentsx.size() // length(x) // vector sizeC.rows() // size(C,1) // number of rowsC.cols() // size(C,2) // number of columnsx(i) // x(i+1) // Matlab is 1-basedC(i, j) // C(i+1,j+1) //A.resize(4, 4); // Runtime error if assertions are on.B.resize(4, 9); // Runtime error if assertions are on.A.resize(3, 3); // Ok; size didn't change.B.resize(3, 9); // Ok; only dynamic cols changed.A << 1, 2, 3, // Initialize A. The elements can also be4, 5, 6, // matrices, which are stacked along cols7, 8, 9; // and then the rows are stacked.B << A, A, A; // B is three horizontally stacked A's.A.fill(10); // Fill A with all 10's.// Eigen // MatlabMatrixXd::Identity(rows, cols) // eye(rows,cols)C.setIdentity(rows, cols) // C = eye(rows,cols)MatrixXd::Zero(rows, cols) // zeros(rows,cols)C.setZero(rows, cols) // C = ones(rows,cols)MatrixXd::Ones(rows, cols) // ones(rows,cols)C.setOnes(rows, cols) // C = ones(rows,cols)MatrixXd::Random(rows, cols) // rand(rows,cols)*2-1 // MatrixXd::Random returns uniform random numbers in (-1, 1).C.setRandom(rows, cols) // C = rand(rows,cols)*2-1VectorXd::LinSpaced(size, low, high) // linspace(low,high,size)'v.setLinSpaced(size, low, high) // v = linspace(low,high,size)'// Matrix slicing and blocks. All expressions listed here are read/write.// Templated size versions are faster. Note that Matlab is 1-based (a size N// vector is x(1)...x(N)).// Eigen // Matlabx.head(n) // x(1:n)x.head<n>() // x(1:n)x.tail(n) // x(end - n + 1: end)x.tail<n>() // x(end - n + 1: end)x.segment(i, n) // x(i+1 : i+n)x.segment<n>(i) // x(i+1 : i+n)P.block(i, j, rows, cols) // P(i+1 : i+rows, j+1 : j+cols)P.block<rows, cols>(i, j) // P(i+1 : i+rows, j+1 : j+cols)P.row(i) // P(i+1, :)P.col(j) // P(:, j+1)P.leftCols<cols>() // P(:, 1:cols)P.leftCols(cols) // P(:, 1:cols)P.middleCols<cols>(j) // P(:, j+1:j+cols)P.middleCols(j, cols) // P(:, j+1:j+cols)P.rightCols<cols>() // P(:, end-cols+1:end)P.rightCols(cols) // P(:, end-cols+1:end)P.topRows<rows>() // P(1:rows, :)P.topRows(rows) // P(1:rows, :)P.middleRows<rows>(i) // P(i+1:i+rows, :)P.middleRows(i, rows) // P(i+1:i+rows, :)P.bottomRows<rows>() // P(end-rows+1:end, :)P.bottomRows(rows) // P(end-rows+1:end, :)P.topLeftCorner(rows, cols) // P(1:rows, 1:cols)P.topRightCorner(rows, cols) // P(1:rows, end-cols+1:end)P.bottomLeftCorner(rows, cols) // P(end-rows+1:end, 1:cols)P.bottomRightCorner(rows, cols) // P(end-rows+1:end, end-cols+1:end)P.topLeftCorner<rows, cols>() // P(1:rows, 1:cols)P.topRightCorner<rows, cols>() // P(1:rows, end-cols+1:end)P.bottomLeftCorner<rows, cols>() // P(end-rows+1:end, 1:cols)P.bottomRightCorner<rows, cols>() // P(end-rows+1:end, end-cols+1:end)// Of particular note is Eigen's swap function which is highly optimized.// Eigen // MatlabR.row(i) = P.col(j); // R(i, :) = P(:, i)R.col(j1).swap(mat1.col(j2)); // R(:, [j1 j2]) = R(:, [j2, j1])// Views, transpose, etc; all read-write except for .adjoint().// Eigen // MatlabR.adjoint() // R'R.transpose() // R.' or conj(R')R.diagonal() // diag(R)x.asDiagonal() // diag(x)R.transpose().colwise().reverse(); // rot90(R)R.conjugate() // conj(R)// All the same as Matlab, but matlab doesn't have *= style operators.// Matrix-vector. Matrix-matrix. Matrix-scalar.y = M * x; R = P * Q; R = P * s;a = b * M; R = P - Q; R = s * P;a *= M; R = P + Q; R = P / s;R *= Q; R = s * P;R += Q; R *= s;R -= Q; R /= s;// Vectorized operations on each element independently// Eigen // MatlabR = P.cwiseProduct(Q); // R = P .* QR = P.array() * s.array();// R = P .* sR = P.cwiseQuotient(Q); // R = P ./ QR = P.array() / Q.array();// R = P ./ QR = P.array() + s.array();// R = P + sR = P.array() - s.array();// R = P - sR.array() += s; // R = R + sR.array() -= s; // R = R - sR.array() < Q.array(); // R < QR.array() <= Q.array(); // R <= QR.cwiseInverse(); // 1 ./ PR.array().inverse(); // 1 ./ PR.array().sin() // sin(P)R.array().cos() // cos(P)R.array().pow(s) // P .^ sR.array().square() // P .^ 2R.array().cube() // P .^ 3R.cwiseSqrt() // sqrt(P)R.array().sqrt() // sqrt(P)R.array().exp() // exp(P)R.array().log() // log(P)R.cwiseMax(P) // max(R, P)R.array().max(P.array()) // max(R, P)R.cwiseMin(P) // min(R, P)R.array().min(P.array()) // min(R, P)R.cwiseAbs() // abs(P)R.array().abs() // abs(P)R.cwiseAbs2() // abs(P.^2)R.array().abs2() // abs(P.^2)(R.array() < s).select(P, Q); // (R < s ? P : Q)// Reductions.int r, c;// Eigen // MatlabR.minCoeff() // min(R(:))R.maxCoeff() // max(R(:))s = R.minCoeff(&r, &c) // [s, i] = min(R(:)); [r, c] = ind2sub(size(R), i);s = R.maxCoeff(&r, &c) // [s, i] = max(R(:)); [r, c] = ind2sub(size(R), i);R.sum() // sum(R(:))R.colwise().sum() // sum(R)R.rowwise().sum() // sum(R, 2) or sum(R')'R.prod() // prod(R(:))R.colwise().prod() // prod(R)R.rowwise().prod() // prod(R, 2) or prod(R')'R.trace() // trace(R)R.all() // all(R(:))R.colwise().all() // all(R)R.rowwise().all() // all(R, 2)R.any() // any(R(:))R.colwise().any() // any(R)R.rowwise().any() // any(R, 2)// Dot products, norms, etc.// Eigen // Matlabx.norm() // norm(x). Note that norm(R) doesn't work in Eigen.x.squaredNorm() // dot(x, x) Note the equivalence is not true for complexx.dot(y) // dot(x, y)x.cross(y) // cross(x, y) Requires #include <Eigen/Geometry>// Eigen // MatlabA.cast<double>(); // double(A)A.cast<float>(); // single(A)A.cast<int>(); // int32(A)A.real(); // real(A)A.imag(); // imag(A)// if the original type equals destination type, no work is done// Note that for most operations Eigen requires all operands to have the same type:MatrixXf F = MatrixXf::Zero(3, 3);A += F; // illegal in Eigen. In Matlab A = A+F is allowedA += F.cast<double>(); // F converted to double and then added (generally, conversion happens on-the-fly)// Eigen can map existing memory into Eigen matrices.float array[3];Vector3f::Map(array).fill(10); // create a temporary Map over array and sets entries to 10int data[4] = { 1, 2, 3, 4 };Matrix2i mat2x2(data); // copies data into mat2x2Matrix2i::Map(data) = 2 * mat2x2; // overwrite elements of data with 2*mat2x2MatrixXi::Map(data, 2, 2) += mat2x2; // adds mat2x2 to elements of data (alternative syntax if size is not know at compile time)// Solve Ax = b. Result stored in x. Matlab: x = A \ b.x = A.ldlt().solve(b)); // A sym. p.s.d. #include <Eigen/Cholesky>x = A.llt().solve(b)); // A sym. p.d. #include <Eigen/Cholesky>x = A.lu().solve(b)); // Stable and fast. #include <Eigen/LU>x = A.qr().solve(b)); // No pivoting. #include <Eigen/QR>x = A.svd().solve(b)); // Stable, slowest. #include <Eigen/SVD>// .ldlt() -> .matrixL() and .matrixD()// .llt() -> .matrixL()// .lu() -> .matrixL() and .matrixU()// .qr() -> .matrixQ() and .matrixR()// .svd() -> .matrixU(), .singularValues(), and .matrixV()// Eigenvalue problems// Eigen // MatlabA.eigenvalues(); // eig(A);EigenSolver<Matrix3d> eig(A); // [vec val] = eig(A)eig.eigenvalues(); // diag(val)eig.eigenvectors(); // vec// For self-adjoint matrices use SelfAdjointEigenSolver<>
}2.4
:
三、new的用法
参考文章 c++中new的作用、C++如何让函数返回数组
//可以在new后面直接赋值int* p = new int(3);//也可以单独赋值//*p = 3;//如果不想使用指针,可以定义一个变量,在new之前用“*”表示new出来的内容int q = *new int;q = 1;cout << q << endl;
3.1 内存的四种分区
栈区(stack): 编译器自动分配和释放的,主要存储的是函数的参数值,局部变量等值。发生函数调用时就为函数运行时用到的数据分配内存,函数调用结束后就将之前分配的内存全部销毁。所以局部变量、参数只在当前函数中有效,不能传递到函数外部。栈内存的大小和编译器有关,编译器会为栈内存指定一个最大值,在 VC/VS 下,默认是 1M。
堆区(heap): 动态分配。一般由程序员分配和释放(动态内存申请malloc与释放free),需要手动free。否则会一直存在,若程序员不释放,程序结束时可能由操作系统回收。
全局区(静态区)(static): 静态分配。全局变量和静态变量的存储是放在一块的,该区域在程序结束后由操作系统释放。
代码区:: 通常用来存放程序执行代码(包含类成员函数和全局函数及其他函数代码),这部分区域的大小在程序运行前就已经确定,也有可能包含一些只读的常数变量,例如字符串变量。
3.2 new的作用

用法示例:
int *a = new int[5];
class A {...} //声明一个类 A
A *obj = new A(); //使用 new 创建对象
delete []a;
delete obj;
3.3
:
3.4
:
四、
4.1
:
4.2
:
4.3
:
4.4
:
总结
:
| 二维数 |
相关文章:

用到的C++的相关知识-----未完待续
文章目录前言一、vector函数的使用1.1 构造向量二、常用函数2.1 矩阵输出函数2.2 向量输出函数2.3 矩阵的使用2.4三、new的用法3.1 内存的四种分区3.2 new的作用3.33.4四、4.14.24.34.4总结前言 只是为方便学习,不做其他用途 一、vector函数的使用 有关的文章 C v…...

JavaScript刷LeetCode拿offer-贪心算法
前言 学习算法的时候,总会有一些让人生畏的名词,比方动态规划,贪心算法 等,听着就很难;而这一 part 就是为了攻破之前一直没有系统学习的 贪心算法; 有一说一,做了这些贪心题,其实…...

selenium
下载并安装selenium 安装:cmd中执行 pip install -i https://pypi.douban.com/simple selenium执行完成后 pip show selenium 可查看安装是否成功安装浏览器驱动,查看当前浏览器的版本选择合适的驱动并下载 chrome的链接:https://chromedrive…...

SpringMVC的视图
转发视图ThymeleafView若使用的视图技术为Thymeleaf,在SpringMVC的配置文件中配置了Thymeleaf的视图解析器,由此视图解析器解析之后所得到的是ThymeleafView。解析:当控制器方法中所设置的视图名称没有任何前缀时,此时的视图名称会…...
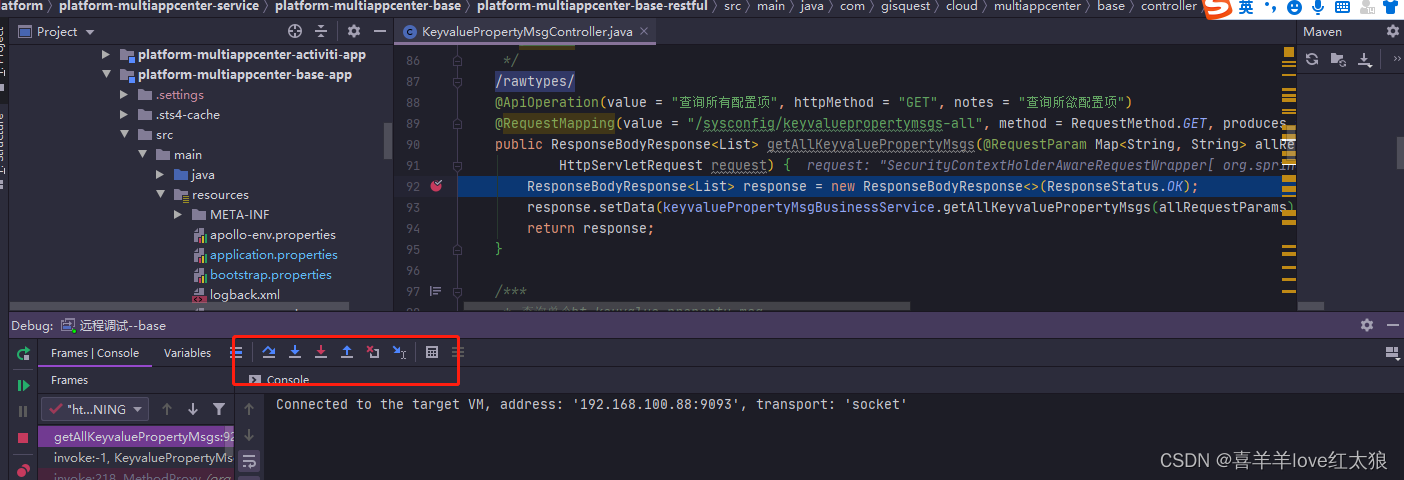
idea使用本地代码远程调试线上运行代码---windows环境
场景: 今天在书上看了一个代码远程调试的方法,自己本地验证了一下感觉十分不错!! windows环境: 启动测试jar包:platform-multiappcenter-base-app-1.0.0-SNAPSHOT.jar 测试工具:postman,idea 应…...
简单记录简单记录
目录1.注册Gmail2.注册ChatGPT3.验证“真人”使用4.开始使用1.注册Gmail 第一步先注册一个谷歌邮箱,你也可以使用微软账号,大部分人选择使用gmail。 申请谷歌邮箱 选择个人用途创建账号即可。 📌温馨提示: 你直接使用guo内的网…...
源码系列 之 ThreadLocal
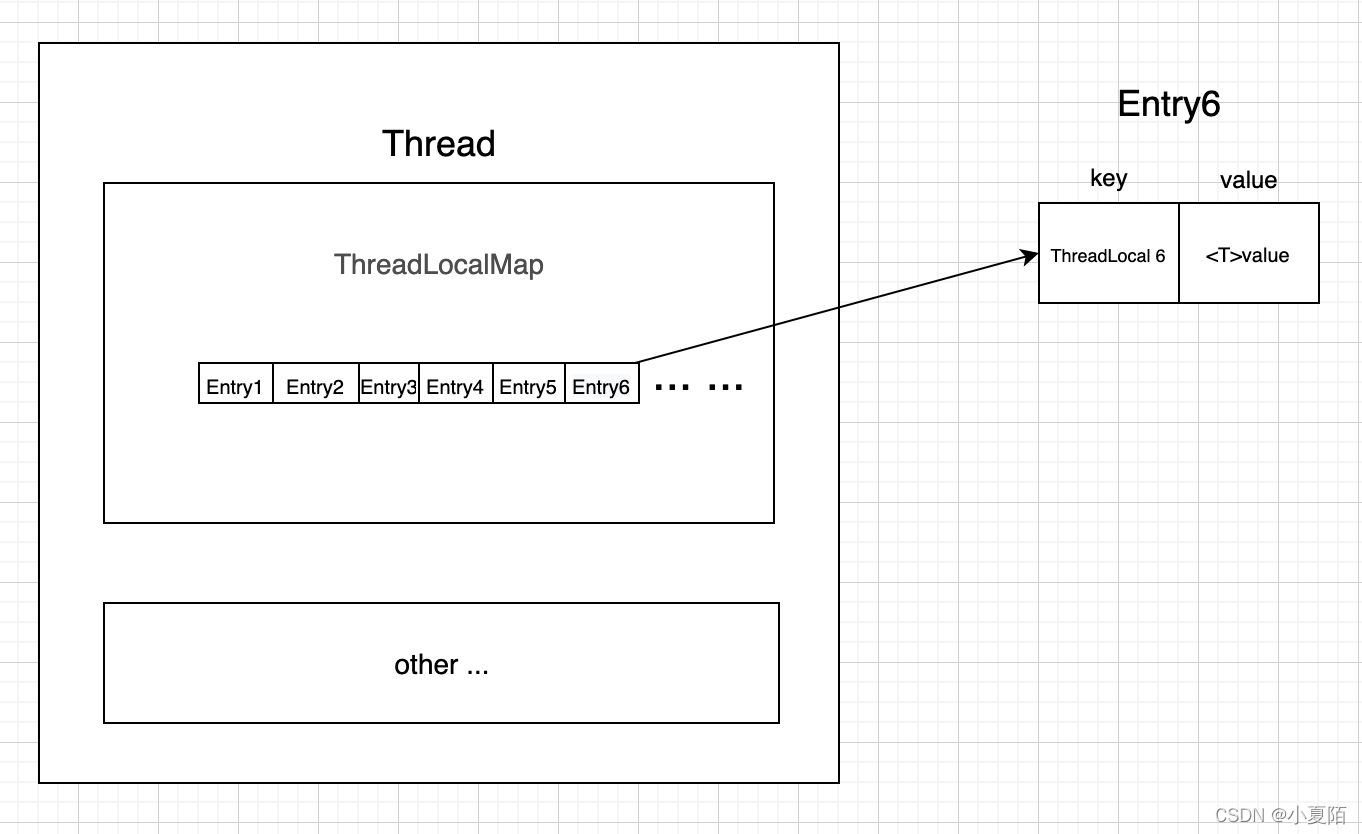
简介 ThreadLocal的作用是做数据隔离,存储的变量只属于当前线程,相当于当前线程的局部变量,多线程环境下,不会被别的线程访问与修改。常用于存储线程私有成员变量、上下文,和用于同一线程,不同层级方法间传…...
——特点及关键字)
C语言入门(1)——特点及关键字
1、C特点及与Java区别 1.1、C特点 面向过程 一般用于嵌入式开发、编写最底层的程序、操作系统 可以直接操作内存 可以封装动态库 不容易跨平台 有指针 可以直接操作串口 线程更加灵活 和硬件打交道速度是最快的 1.2、和Java区别 C是C的增强版,增加了一些新的特性&…...

react中useEffect和useLayoutEffect的区别
布局上 useEffect在浏览器渲染完成后执行useLayoutEffect在DOM更新后执行 特点 useLayoutEffect 总是比 useEffect 先执行;useLayoutEffect与componentDidMount、componentDidUpdate调用时机相同,都是在DOM更新后,页面渲染前调用࿱…...

NoSQL(非关系型数据库)与SQL(关系型数据库)的差别
目录 NoSQL(非关系型数据库)与SQL(关系型数据库)的差别 1.数据结构:结构化与非结构化 2.数据关联:关联性与非关联性 3.查询方式:SQL查询与非SQL查询 4.事务特性:ACID与BASE 分析ACID与BASE的含义: 5.存储方式&am…...

new bing的申请与使用教程
文章目录新必应申请新必应免代使用教程总结新必应申请 下载安装 Edge dev 版本,这个版本可以直接使用 对于没有更新的用户而言,不容易找到入口,所以我们直接使用 集成new bing的dev版本 Edge dev 下载链接:https://www.microso…...

yaml配置文件
最近在写代码,发现随着网络的增加,代码变得越来越冗余,所以就想着写一个网络的配置文件,把网络的配置放到一个文件中,而不再主函数中,这样代码开起来就好看了,调试的时候也方便了。之前写过一篇…...

284. 顶端迭代器
请你在设计一个迭代器,在集成现有迭代器拥有的 hasNext 和 next 操作的基础上,还额外支持 peek 操作。 实现 PeekingIterator 类: PeekingIterator(Iterator nums) 使用指定整数迭代器 nums 初始化迭代器。 int next() 返回数组中的下一个元…...

自学前端最容易犯的10个的错误,入门学前端快来看看
在前端学习过程中,有很多常见的误区,包括过度关注框架和库、缺乏实践、忽视算法和数据结构、忽视浏览器兼容性、缺乏团队合作经验、忽视可访问性、重构次数过多、没有关注性能、缺乏设计知识以及没有持续学习等。要避免这些误区,应该注重基础…...
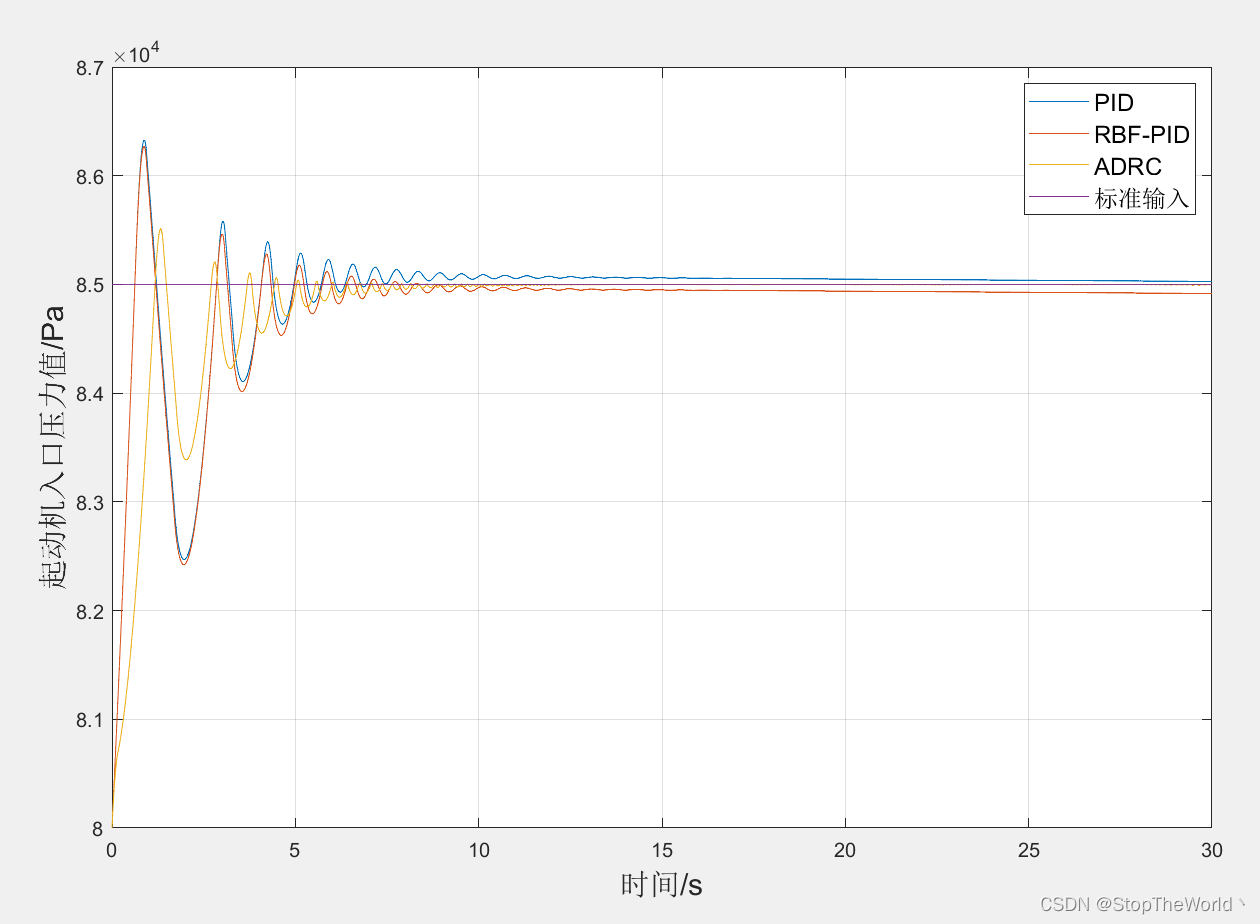
【ADRC控制】使用自抗扰控制器调节起动机入口压力值
以前只知道工业控制中用的是PID控制,然而最近了解到实际生产中还在使用ADRC控制,而且使用效果还优于PID控制,遂找了几篇文献学习学习。 0 引言 自抗扰控制(Active Disturbances Rejection Controller,ADRC)…...
)
剑指 Offer Day2——链表(简单)
目录剑指 Offer 06. 从尾到头打印链表剑指 Offer 24. 反转链表剑指 Offer 35. 复杂链表的复制剑指 Offer 06. 从尾到头打印链表 原题链接:06. 从尾到头打印链表 最容易想到的思路就是先从头到尾打印下来,然后 reverse 一下,但这里我们使用递归…...

Final Cut Pro 10.6.5
软件介绍Final Cut Pro 10.6.5 已通过小编安装运行测试 100%可以使用。Final Cut Pro 10.6.5 破解版启用了全新的矩形图标,与最新的macOS Ventura设计风格统一,支持最新的macOS 13 文图拉系统,支持Apple M1/M2芯片。经过完整而彻底的重新设计…...
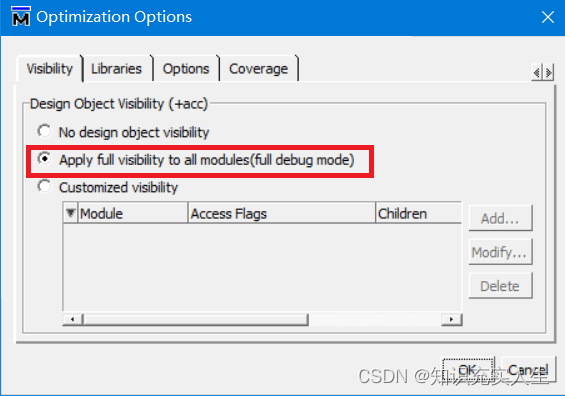
Modelsim仿真操作指导
目录 一、前言 二、仿真分类 三、RTL级仿真 3.1创建库 3.2 仿真配置设置 3.3 运行仿真 四、常见问题 4.1 运行仿真时报错“cant read "Startup(-L)": no such element in array” 4.2 运行仿真时无任何报错,但object窗口为空,可正常运…...

你知道这20个数组方法是怎么实现的吗?
前言你们一定对JavaScript中的数组很熟悉,我们每天都会用到它的各种方法,比如push、pop、forEach、map……等等。但是仅仅使用它就足够了吗?如此出色,您一定不想停在这里。我想和你一起挑战实现20数组方法的功能。1、forEachforEa…...

《系统架构设计》-01-架构和架构师概述
文章目录1. 架构的基本定义1.1 架构组成理论1.1.1 系统元素1)概念2)静态结构和动态结构1.1.2 基本系统属性1.1.3 设计和发展原则1.2 架构的决策理论1.2.1 统一软件过程(Rational Unified Process,统一软件过程)1.2.2 决…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
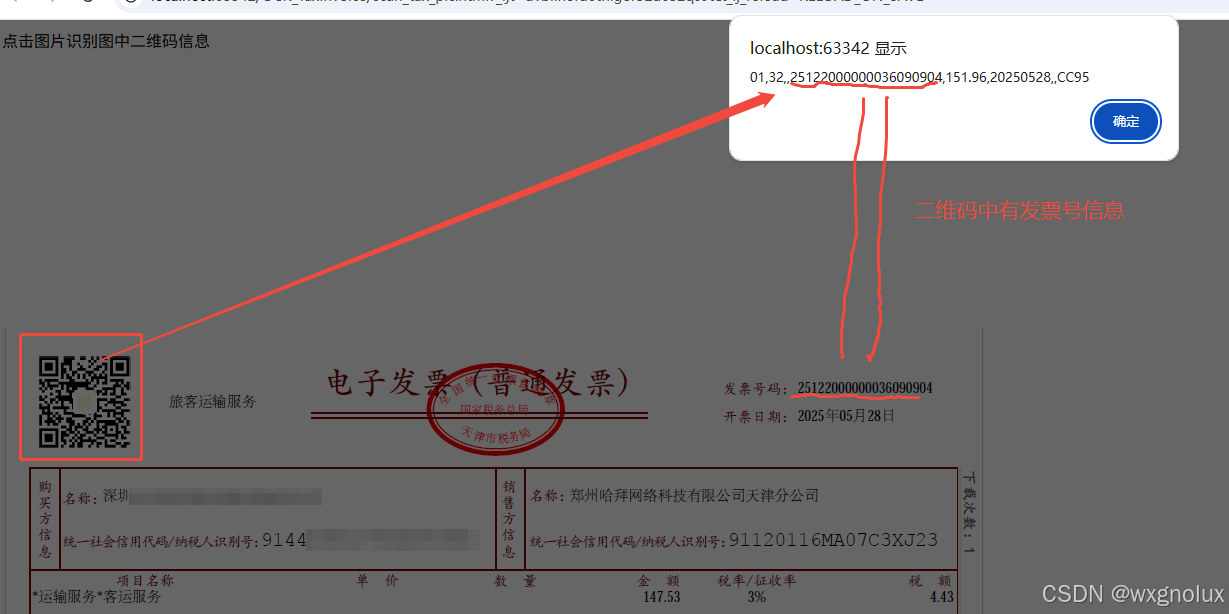
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
