16- 梯度提升分类树GBDT (梯度下降优化) (算法)
-
梯度提升算法
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(subsample=0.8,learning_rate = 0.005)
clf.fit(X_train,y_train)1、交叉熵
1.1、信息熵
- 构建好一颗树,数据变的有顺序了(构建前,一堆数据,杂乱无章;构建一颗,整整齐齐,顺序),用什么度量衡表示,数据是否有顺序:信息熵
- 物理学,热力学第二定律(熵),描述的是封闭系统的混乱程度
- 信息熵,和物理学中熵类似的
1.2、交叉熵
由信息熵可以引出交叉熵!
小明在学校玩王者荣耀被发现了,爸爸被叫去开家长会,心里悲屈的很,就想法子惩罚小明。到家后,爸爸跟小明说:既然你犯错了,就要接受惩罚,但惩罚的程度就看你聪不聪明了。这样吧,我们俩玩猜球游戏,我拿一个球,你猜球的颜色,我可以回答你任何问题,你每猜一次,不管对错,你就一个星期不能玩王者荣耀,当然,猜对,游戏停止,否则继续猜。当然,当答案只剩下两种选择时,此次猜测结束后,无论猜对猜错都能100%确定答案,无需再猜一次,此时游戏停止。
1.2.1、题目一
爸爸拿来一个箱子,跟小明说:里面有橙、紫、蓝及青四种颜色的小球任意个,各颜色小球的占比不清楚,现在我从中拿出一个小球,你猜我手中的小球是什么颜色?
为了使被罚时间最短,小明发挥出最强王者的智商,瞬间就想到了以最小的代价猜出答案,简称策略1,小明的想法是这样的。

1.2.2、题目二
爸爸还是拿来一个箱子,跟小明说:箱子里面有小球任意个,但其中1/2是橙色球,1/4是紫色球,1/8是蓝色球及1/8是青色球。我从中拿出一个球,你猜我手中的球是什么颜色的?
小明毕竟是最强王者,仍然很快得想到了答案,简称策略2,他的答案是这样的。

这就需要引入交叉熵,其用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
1.3、sigmoid
后面算法推导过程中都会使用到上面的基本方程,因此先对以上概念公式,有基本了解!
2、GBDT分类树
2.1、梯度提升分类树概述
GBDT分类树 sigmoid + 决策回归树 一一> 概率问题!
-
损失函数是交叉熵
-
概率计算使用sigmoid
-
使用 mse 作为分裂标准(同梯度提升回归树)
2.2、梯度提升分类树应用
1、加载数据
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.tree import DecisionTreeClassifierX,y = datasets.load_iris(return_X_y = True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 1124)2、普通决策树表现
model = DecisionTreeClassifier()
model.fit(X_train,y_train)
model.score(X_test,y_test) # 输出:0.84210526315789473、梯度提升分类树表现
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(subsample=0.8,learning_rate = 0.005)
clf.fit(X_train,y_train)
clf.score(X_test,y_test) # 输出:0.94736842105263153、GBDT分类树算例演示
3.1、算法公式
-
概率计算(sigmoid函数)
-
函数初始值(这个函数即是sigmoid分母中的F(x),用于计算概率)
逻辑回归中的函数是线性函数,GBDT中的函数不是线性函数,但是作用类似!
-
计算残差公式
-
均方误差(根据均方误差,筛选最佳裂分条件)
-
决策树叶节点预测值(相当于负梯度)
-
梯度提升
-
根据以上公式,即可进行代码演算了~
3.2、算例演示
3.2.1、创建数据
import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn import tree
import graphviz
X = np.arange(1,11).reshape(-1,1)
y = np.array([0,0,0,1,1]*2)
display(X,y)3.2.2、构造GBDT训练预测
# 默认情况下,损失函数就是Log-loss == 交叉熵!
clf = GradientBoostingClassifier(n_estimators=3,learning_rate=0.1,max_depth=1)
clf.fit(X,y)
y_ = clf.predict(X)
print('真实的类别:',y)
print('算法的预测:',y_)
proba_ = clf.predict_proba(X)
print('预测概率是:\n',proba_)3.2.3、GBDT可视化
第一棵树
dot_data = tree.export_graphviz(clf[0,0],filled = True)
graph = graphviz.Source(dot_data)
graph第二棵树
dot_data = tree.export_graphviz(clf[1,0],filled = True)
graph = graphviz.Source(dot_data)
graph第三棵树
dot_data = tree.export_graphviz(clf[2,0],filled = True)
graph = graphviz.Source(dot_data)
graph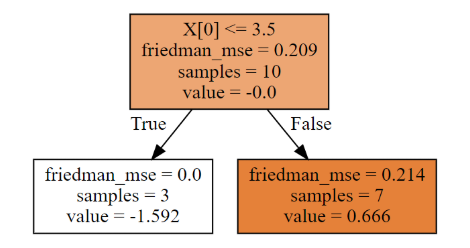
每棵树,根据属性进行了划分,每棵树的叶节点都有预测值,这些具体都是如何计算的呢?且看,下面详细的计算工程~
3.2.4、计算步骤
首先,计算初始值 :
F0 = np.log(y.sum()/(1-y).sum())
F0 # 输出结果:-0.40546510810816444
# 此时未裂分,所有的数据都是F0
F0 = np.array([F0]*10)
# 然后,计算残差
# 残差,F0带入sigmoid计算的即是初始概率
residual0 = y - 1/(1 + np.exp(-F0))
residual0
# 输出:array([-0.4, -0.4, -0.4, 0.6, 0.6, -0.4, -0.4, -0.4, 0.6, 0.6])3.2.5、拟合第一棵树
根据残差的mse,计算最佳分裂条件
lower_mse = ((residual0 - residual0.mean())**2).mean()
best_split = {}
# 分裂标准 mse
for i in range(0,10):if i == 9:mse = ((residual0 - residual0.mean())**2).mean()else:left_mse = ((residual0[:i+1] - residual0[:i+1].mean())**2).mean()right_mse = ((residual0[i+1:] - residual0[i+1:].mean())**2).mean()mse = left_mse*(i+1)/10 + right_mse*(10-i-1)/10if lower_mse > mse:lower_mse = msebest_split.clear()best_split['X[0] <= '] = X[i:i + 2].mean() print('从第%d个进行分裂'%(i + 1),np.round(mse,4))
# 从第八个样本这里进行分类,最优的选择,和算法第一颗画图的结果一致
print('最小的mse是:',lower_mse)
print('最佳裂分条件是:',best_split)
现在我们知道了,分裂条件是:X[0] <= 8.5!然后计算决策树叶节点预测值(相当于负梯度),其中的 就是残差residual0
3.2.6、拟合第二棵树
第一棵树的负梯度(预测值)
# 第一棵预测的结果,负梯度
gamma = np.array([gamma1]*8 + [gamma2]*2)
gamma '''输出:array([-0.625, -0.625, -0.625, -0.625, -0.625, -0.625,-0.625, -0.625, 2.5 , 2.5 ])'''梯度提升
# F(x) 随着梯度提升树,提升,发生变化
learning_rate = 0.1
F1 = F0 + gamma*learning_rate
F1 ''' 输出 array([-0.46796511, -0.46796511, -0.46796511, -0.46796511,
-0.46796511, -0.46796511, -0.46796511, -0.46796511, -0.15546511, -0.15546511])'''根据 F1 计算残差
residual1 = y - 1/(1 + np.exp(-F1))
residual1 '''array([-0.38509799, -0.38509799, -0.38509799, 0.61490201,
0.61490201, -0.38509799, -0.38509799, -0.38509799, 0.53878818, 0.53878818])'''根据新的残差residual1的mse,计算最佳分裂条件
lower_mse = ((residual1 - residual1.mean())**2).mean()
best_split = {}
# 分裂标准 mse
for i in range(0,10):if i == 9:mse = ((residual1 - residual1.mean())**2).mean()else:left_mse = ((residual1[:i+1] - residual1[:i+1].mean())**2).mean()right_mse = ((residual1[i+1:] - residual1[i+1:].mean())**2).mean()mse = left_mse*(i+1)/10 + right_mse*(10-i-1)/10if lower_mse > mse:lower_mse = msebest_split.clear()best_split['X[0] <= '] = X[i:i + 2].mean() print('从第%d个进行分裂'%(i + 1),np.round(mse,4))
# 从第八个样本这里进行分类,最优的选择,和算法第一颗画图的结果一致
print('最小的mse是:',lower_mse)
print('最佳裂分条件是:',best_split)现在我们知道了,第二棵树分裂条件是:X[0] <= 8.5 !然后计算决策树叶节点预测值(相当于负梯度),其中的 就是残差residual1
3.2.7、拟合第三棵树
第二棵树的负梯度
# 第二棵树预测值
gamma = np.array([gamma1]*8 + [gamma2]*2)
gamma梯度提升
# F(x) 随着梯度提升树,提升,发生变化
learning_rate = 0.1
F2 = F1 + gamma*learning_rate
F2根据 F2 计算残差
residual2 = y - 1/(1 + np.exp(-F2))
residual2根据新的残差residual2的 mse,计算最佳分裂条件
lower_mse = ((residual2 - residual2.mean())**2).mean()
best_split = {}
# 分裂标准 mse
for i in range(0,10):if i == 9:mse = ((residual2 - residual2.mean())**2).mean()else:left_mse = ((residual2[:i+1] - residual2[:i+1].mean())**2).mean()right_mse = ((residual2[i+1:] - residual2[i+1:].mean())**2).mean()mse = left_mse*(i+1)/10 + right_mse*(10-i-1)/10if lower_mse > mse:lower_mse = msebest_split.clear()best_split['X[0] <= '] = X[i:i + 2].mean() print('从第%d个进行分裂'%(i + 1),np.round(mse,4))
# 从第八个样本这里进行分类,最优的选择,和算法第一颗画图的结果一致
print('最小的mse是:',lower_mse)
print('最佳裂分条件是:',best_split)现在我们知道了,第三棵树分裂条件是:X[0] <= 3.5!然后计算决策树叶节点预测值(相当于负梯度),其中的 就是残差residual2
# 计算第三颗树的预测值
# 前三个是一类
# 后七个是一类
# 左边分支
gamma1 = residual2[:3].sum()/((y[:3] - residual2[:3])*(1 - y[:3] +
residual2[:3])).sum()
print('第三棵树左边决策树分支,预测值:',gamma1)# 右边分支
gamma2 =residual2[3:].sum()/((y[3:] - residual2[3:])*(1 - y[3:] +
residual2[3:])).sum()
print('第三棵树右边决策树分支,预测值:',gamma2)3.2.8、预测概率计算
计算第三棵树的F3(x)
# 第三棵树预测值
gamma = np.array([gamma1]*3 + [gamma2]*7)
# F(x) 随着梯度提升树,提升,发生变化
learning_rate = 0.1
F3 = F2 + gamma*learning_rate概率公式如下:
proba = 1/(1 + np.exp(-F3))
# 类别:0,1,如果这个概率大于等于0.5类别1,小于0.5类别0
display(proba)
# 进行转换,类别0,1的概率都展示
np.column_stack([1- proba,proba])
# 算法预测概率
clf.predict_proba(X)结论:
-
手动计算的概率和算法预测的概率完全一样!
-
GBDT分类树,计算过程原理如上
4、GBDT分类树原理推导
4.1、损失函数:
-
定义交叉熵为函数
其中 ,即sigmoid函数
表示决策回归树 DecisionTreeRegressor F(x) 表示每一轮决策树的value,即负梯度
4.2、损失函数化简
-
损失函数化简:
-
-
化简过程
4.3、损失函数求导
将F(x)看成整体变量,进行求导
一阶导数:
4.4、初始值  计算
计算
4.4.1、初始值方程构建
之前的GBDT回归树,初始值是多少:平均值
现在的GBDT分类树 ,计算初始值 ,令
5、GBDT二分类步骤总结
Step - 1:
Step - 2:for i in range(M):
a.
b. 根据残差 ,寻找最小 mse 裂分条件
c.
d.
相关文章:
16- 梯度提升分类树GBDT (梯度下降优化) (算法)
梯度提升算法 from sklearn.ensemble import GradientBoostingClassifier clf GradientBoostingClassifier(subsample0.8,learning_rate 0.005) clf.fit(X_train,y_train) 1、交叉熵 1.1、信息熵 构建好一颗树,数据变的有顺序了(构建前,…...
SpringCloud+Nacos+Gateway
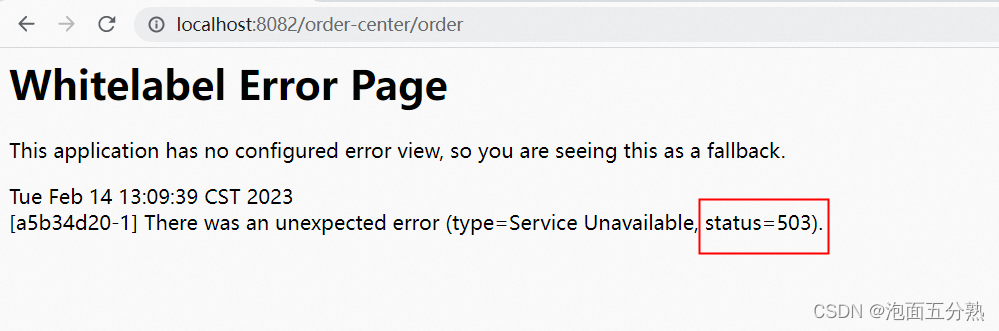
SpringCloudNacosGatewaySpringBoot整合GatewayNacos一. 环境准备1. 版本环境2. 服务环境二. 实战1.创建用户服务2.创建订单服务3.创建网关服务4.测试三. 避坑指南问题1--503问题问题2--网关服务启动报错SpringBoot整合GatewayNacos 本篇文章只演示通过gateway网关服务访问其他…...
高通开发系列 - linux kernel内核升级msm-3.18升至msm-4.9(2)
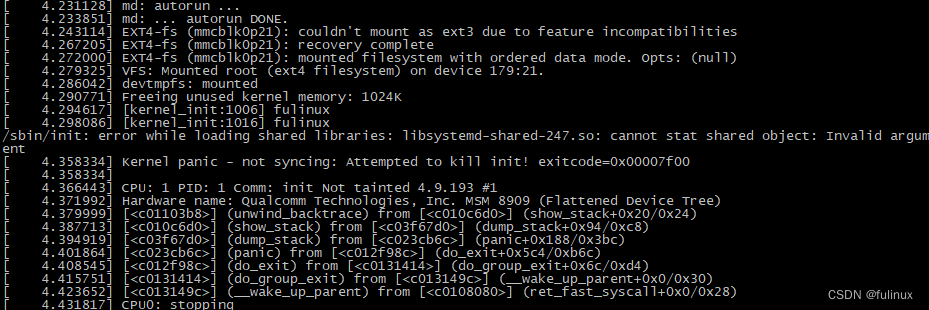
By: fulinux E-mail: fulinux@sina.com Blog: https://blog.csdn.net/fulinus 喜欢的盆友欢迎点赞和订阅! 你的喜欢就是我写作的动力! 目录 返回高通开发系列 - 总目录 前面我们升级了msm-4.9内核系统正常启动了,文件系统也正常工作,但那是使用了老基线的文件系统,其yocto…...

Spring依赖注入与反转控制到底是个啥?
目录 1. 引言 2. 管中窥豹 3.1 Spring 依赖注入 3.2 Bean 的依赖注入方式有两种 4. 总结 1. 引言 此文目的是用通俗易懂的语言讲清楚什么是依赖注入与反转控制,在看了大量的博客文章后归纳总结,便于后续巩固!我相信,大多数…...

Linux Shell脚本讲解
目录 Shell脚本基础 Shell脚本组成 Shell脚本工作方式 编写简单的Shell脚本 Shell脚本参数 Shell脚本接收参数 Shell脚本判断用户参数 文件测试与逻辑测试语句 整数测试比较语句 字符串比较语句 Shell流程控制 if条件判断语句 单分支 双分支 多分支 for循环语句…...
Linux:用户空间非法指针coredump简析
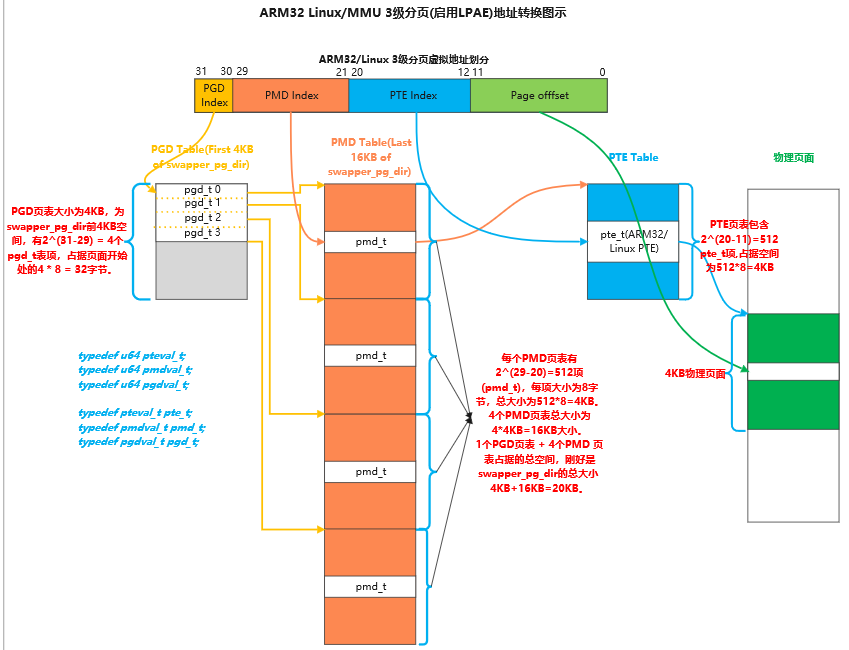
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 背景 本文分析基于 ARM32 架构,Linux-4.14 内核代码。 3. 问题分析 3.1 测试范例 void main(void) {*(int *)0 8; }运行程序会 …...
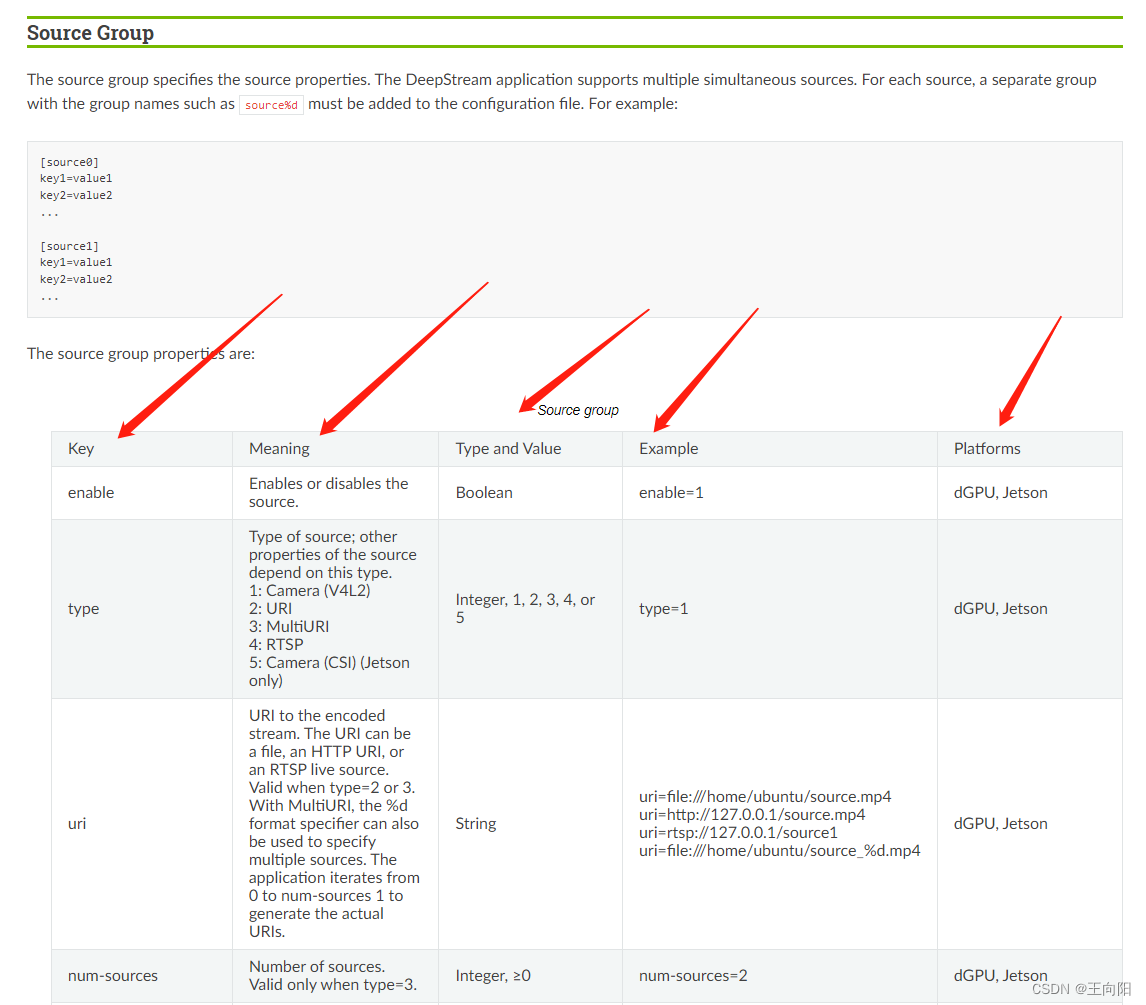
带你玩转Jetson之Deepstream简明教程(四)DeepstreamApp如何使用以及用于工程验证。
1.DeepstreamApp是什么? 如果你安装完毕deepstream整体框架,会在你的系统执行目录内有可执行文件,文件名字是deepstream-app。这是一个可执行脚本文件,通过deepstream框架中的代码在安装的时候编译后install到系统根目录内。 此脚…...
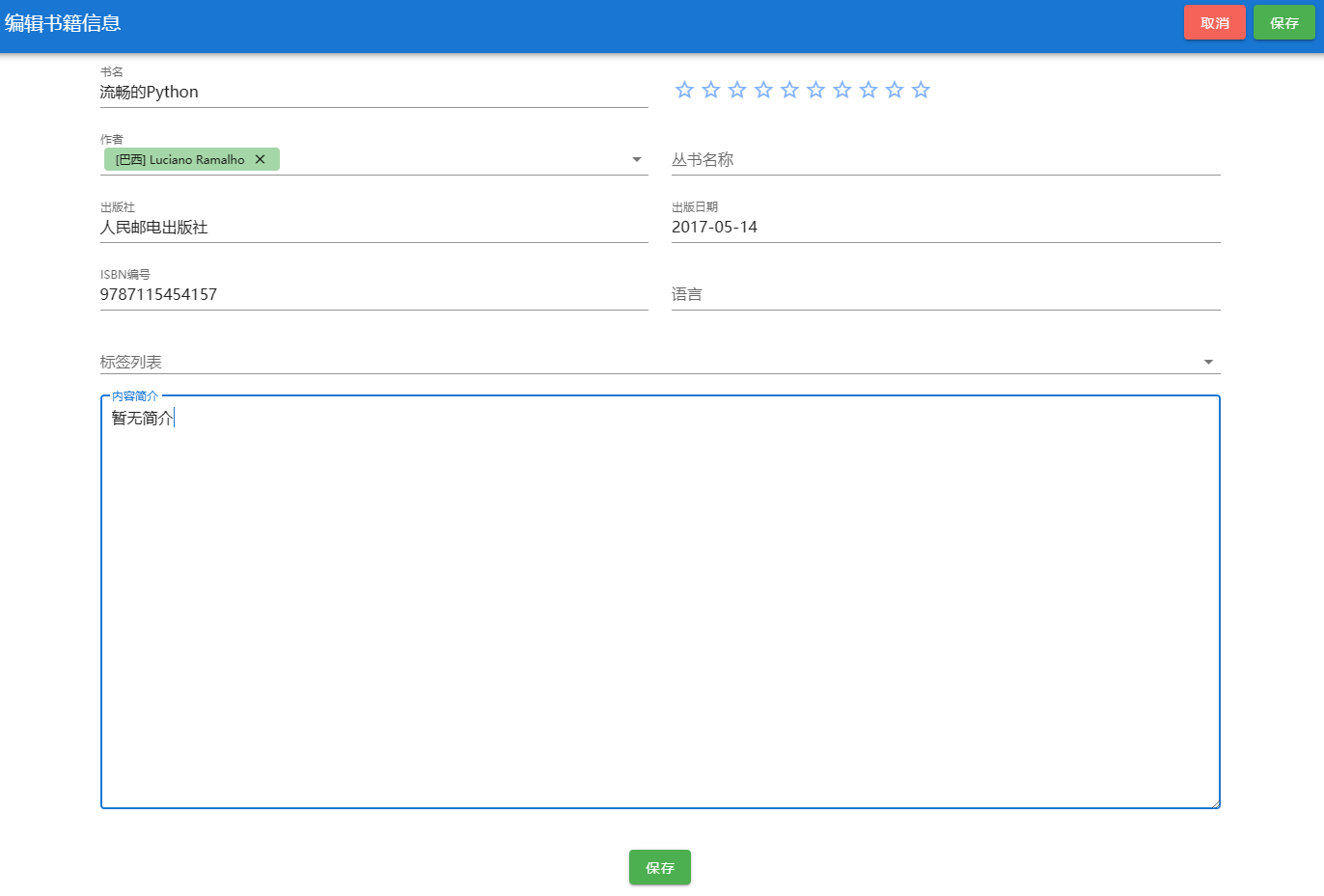
快速搭建个人在线书库,随时随地畅享阅读!
前边我们利用NAS部署了个人的导航页、小说站、云笔记,今天,我们再看看怎么部署一个个人的在线书库。 相信很多朋友都在自己的电脑中收藏了大量的PDF、MOBI等格式的电子书籍,但是一旦换了一台设备,要么是无法翻阅,要么…...

电子纸墨水屏的现实应用场景
电子纸挺好个东西,大家都把注意力集中在商超场景 其实还有更多有趣的场景方案可用,价值也不小,比如: 一、仓库场景 通过亮灯拣选,提高仓库作业效率 二、仓库循环使用标签 做NFC类发卡式应用,替代传统纸…...
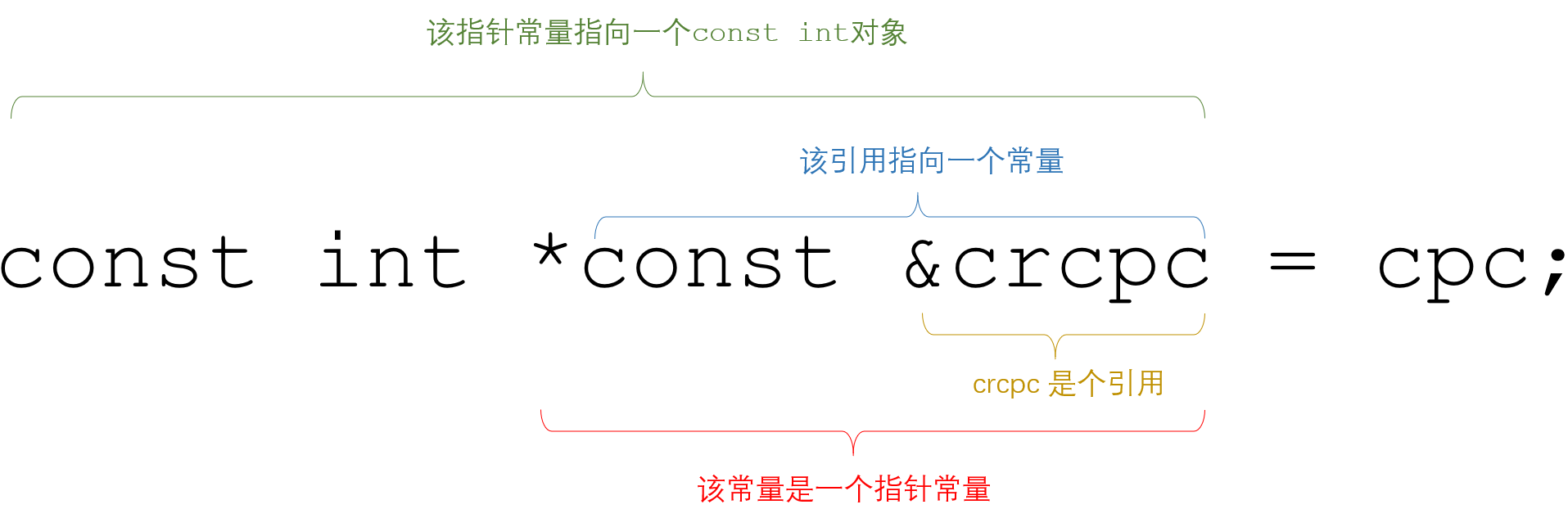
常量const、引用、指针的大杂烩
文章目录1 普通引用1.1 对普通值的普通引用1.2 对常量值的普通引用1.3 对普通指针的普通引用1.4 对常量指针的普通引用1.5 对指针常量的普通引用1.6 对指向常量的指针常量的普通引用2 常量引用2.1 对普通值的常量引用2.2 对常量值的常量引用2.3 对普通指针的常量引用2.4 对常量…...
宝塔搭建实战php开源likeadmin通用管理移动端uniapp源码(四)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享了pc端的部署方式,今天来给大家分享uniapp端在本地搭建,与打包发布到宝塔的方法。感兴趣的朋友可以自行下载学习。 技术架构 vscode node16 vue3 uniapp vite types…...

Hive的分区表与分桶表内部表外部表
文章目录1 Hive分区表1.1 Hive分区表的概念?1.1.1 分区表注意事项1.2 分区表物理存储结构1.3 分区表使用场景1.4 静态分区表是什么?1.4.1 静态分区表案例1.4.2 分区表练习一1.4.3 分区操作1.5 动态分区表是什么?1.5.1 动态态分区表案例&#…...

和数集团打造《神念无界:源起山海》,诠释链游领域创新与责任
首先,根据网上资料显示,一部《传奇》,二十年热血依旧。 《传奇》所缔造的成绩,承载的是多少人的青春回忆,《传奇》无疑已经在游戏史上写下了浓墨重彩的一笔。 相比《传奇》及背后的研发运营公司娱美德名声大噪&#x…...

小白入门模拟IC设计,如何快速学习?
众所周知,模拟电路很难学。以最普遍的晶体管来说,我们分析它的时候必须首先分析直流偏置,其次在分析交流输出电压。可以说,确定工作点就是一项相当麻烦的工作(实际中来说),晶体管的参数多、参数…...
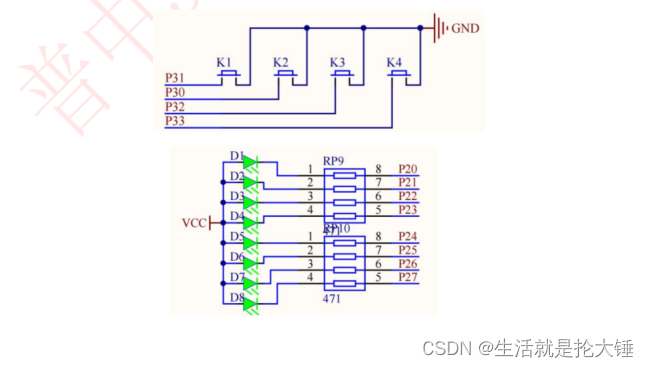
51单片机——中断系统之外部中断实验,小白讲解,相互学习
中断介绍 中断是为使单片机具有对外部或内部随机发生的事件实时处理而设置的,中断功能的存在,很大程度上提高了单片机处理外部或内部事件的能力。它也是单片机最重要的功能之一,是我们学些单片机必须要掌握的。 为了更容易的理解中断概念&…...
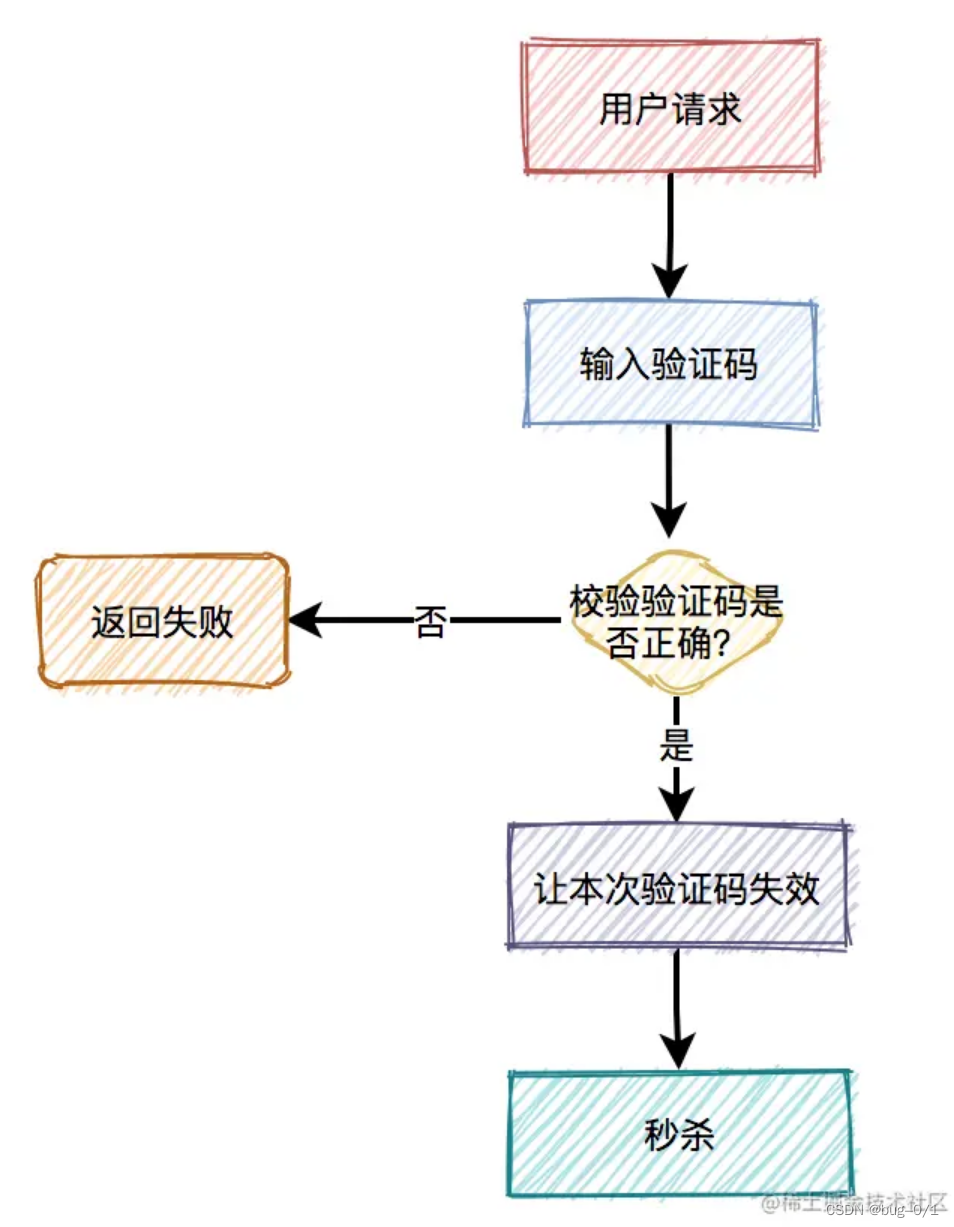
如何设计一个秒杀系统
秒杀系统要如何设计? 前言 高并发下如何设计秒杀系统?这是一个高频面试题。这个问题看似简单,但是里面的水很深,它考查的是高并发场景下,从前端到后端多方面的知识。 秒杀一般出现在商城的促销活动中,指定…...

厄瓜多尔公司注册方案
简介: 经济概况与商机 厄瓜多尔是世界上第74大国家,是南美西部国家,与哥伦比亚,秘鲁和太平洋接壤。厄瓜多尔地处世界中心,地理位置优越,地理位置优越-赤道线零纬度,使其成为通往太平洋的理想枢…...
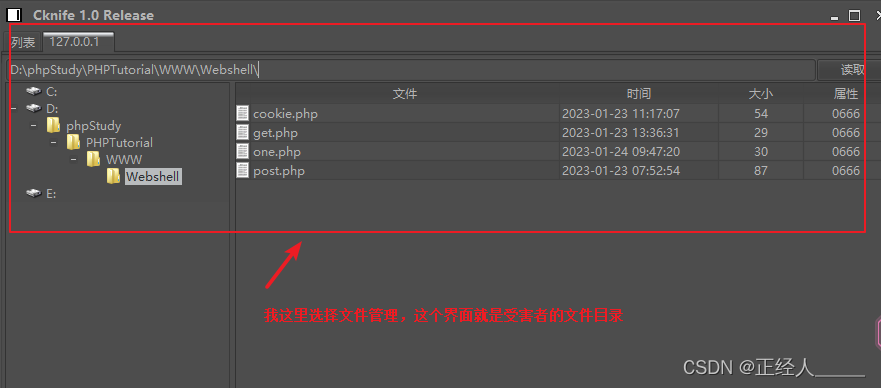
安全渗透环境准备(工具下载)
数据来源 01 一些VM虚拟机的安装 攻击机kali: kali官网 渗透测试工具Kali Linux安装与使用 kali汉化 虚拟机网络建议设置成NAT模式,桥接有时不稳定。 靶机OWASP_Broken_Web_Apps: 迅雷下载 网盘下载 安装教程 开机之后需要登录&am…...

118.(leaflet篇)leaflet空间判断-点与geojson面图层的空间关系(turf实现)
听老人家说:多看美女会长寿 地图之家总目录(订阅之前建议先查看该博客) 文章末尾处提供保证可运行完整代码包,运行如有问题,可“私信”博主。 效果如下所示: 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYPE html> <html>...

目标检测与目标跟踪算法技术汇总
现如今chatgpt的爆火,我也使用了一段时间,问了许多关于人工智能技术的问题,基本是它能够回答了大部分的原理的,至于其人工智能涉及到的算法以及网络,考虑到也没有图,可能在给出这类回答上,是不太…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
