Python优化算法—遗传算法
Python优化算法—遗传算法
- 一、前言
- 二、安装
- 三、遗传算法
- 3.1 自定义函数
- 3.2 遗传算法进行整数规划
- 3.3 遗传算法用于旅行商问题
- 3.4 使用遗传算法进行曲线拟合
一、前言
优化算法,尤其是启发式的仿生智能算法在最近很火,它适用于解决管理学,运筹学,统计学里面的一些优化问题。比如线性规划,整数规划,动态规划,非线性约束规划,甚至是超参数搜索等等方向的问题。
但是一般的优化算法还是matlab里面用的多,Python相关代码较少。
我在参考了一些文章的代码和模块之后,决定学习scikit-opt这个模块。这个优化算法模块对新手很友好,代码简洁,上手简单。而且代码和官方文档是中国人写的,还有很多案例,学起来就没什么压力。
缺点是包装的算法种类目前还不算多,只有七种:(差分进化算法、遗传算法、粒子群算法、模拟退火算法、蚁群算法、鱼群算法、免疫优化算法)
本次带来的是数学建模里面经常使用的遗传算法的使用演示。
二、安装
首先安装模块,在cmd里面或者anaconda prompt里面输入:
pip install scikit-opt
对于当前开发人员版本:
git clone git@github.com:guofei9987/scikit-opt.git
cd scikit-opt
pip install .
三、遗传算法
3.1 自定义函数
UDF(用户定义函数)现已推出!
例如,您刚刚制定了一种新型函数。现在,你的函数是这样的:
f=0.5+sin2(x12+x22)−0.51+0.001(x12+x22)f = 0.5 + \frac{sin^2(x_1^2 + x_2^2) - 0.5}{1 + 0.001 (x_1^2 + x_2^2)} f=0.5+1+0.001(x12+x22)sin2(x12+x22)−0.5
该函数有大量的局部最小值,具有很强的冲击力,在(0,0) 处的全局最小值,值为 0。
import numpy as np
def schaffer(p):x1, x2 = px = np.square(x1) + np.square(x2)return 0.5 + (np.square(np.sin(x)) - 0.5) / np.square(1 + 0.001 * x)
导入和构建 ga :(遗传算法)
from sko.GA import GA
ga = GA(func=schaffer, n_dim = 2, size_pop = 100, max_iter = 800, prob_mut = 0.001, lb = [-1, -1], ub = [1, 1], precision = 1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
运行结果为:

可以看到基本找到了全局最小值和对应的x 。
画出迭代次数的图:
import pandas as pd
import matplotlib.pyplot as plt
Y_history = pd.DataFrame(ga.all_history_Y)
fig, ax = plt.subplots(2, 1)
ax[0].plot(Y_history.index, Y_history.values, '.', color = 'red')
Y_history.min(axis = 1).cummin().plot(kind = 'line')
plt.show()

GA算法的参数详解:
输入参数:
| 输入参数 | 默认值 | 参数的意义 |
|---|---|---|
| func | - | 目标函数 |
| n_dim | - | 目标函数的维度 |
| size_pop | 50 | 种群规模 |
| max_iter | 200 | 最大迭代次数 |
| prob_mut | 0.001 | 变异概率 |
| lb | -1 | 每个自变量的最小值 |
| ub | 1 | 每个自变量的最大值 |
| constraint_eq | 空元组 | 等式约束 |
| constraint_ueq | 空元组 | 不等式约束 |
| precision | 1e-7 | 精确度,int / float或者它们组成的列表 |
输出参数:
GA & GA_TSP
| 输出参数 | 参数的意义 |
|---|---|
| ga.generation_best_X | 每一代的最优函数值对应的输入值 |
| ga.generation_best_Y | 每一代的最优函数值 |
| ga.all_history_FitV | 每一代的每个个体的适应度 |
| ga.all_history_Y | 每一代每个个体的函数值 |
3.2 遗传算法进行整数规划
在多维优化时,想让哪个变量限制为整数,就设定 precision 为 整数 即可。
例如,我想让我的自定义函数的某些变量限制为整数+浮点数(分别是整数,整数,浮点数),那么就设定 precision=[1, 1, 1e-7]
例子如下:
from sko.GA import GA
demo_func = lambda x: (x[0] - 1) ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2
ga = GA(func = demo_func, n_dim = 3, max_iter = 500, lb = [-1, -1, -1], ub = [5, 1, 1], precision = [1,1,1e-7])
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)

可以看到第一个、第二个变量都是整数,第三个就是浮点数了 。
3.3 遗传算法用于旅行商问题
商旅问题(TSP)就是路径规划的问题,比如有很多城市,你都要跑一遍,那么先去哪个城市再去哪个城市可以让你的总路程最小。
实际问题需要一个城市坐标数据,比如你的出发点位置为(0,0),第一个城市离位置为(x1,y1)(x_1,y_1)(x1,y1),第二个为(x2,y2)(x_2,y_2)(x2,y2)…这里没有实际数据,就直接随机生成了。
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
num_points = 50
points_coordinate = np.random.rand(num_points, 2) # generate coordinate of points
points_coordinate

这里定义的是50个城市,每个城市的坐标都在是上图随机生成的矩阵。
然后我们把它变成类似相关系数里面的矩阵:
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
distance_matrix.shape
(50, 50)
这个矩阵就能得出每个城市之间的距离,算上自己和自己的距离(0),总共有2500个数。
定义问题:
def cal_total_distance(routine):num_points, = routine.shapereturn sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
求解问题:
from sko.GA import GA_TSP
ga_tsp = GA_TSP(func = cal_total_distance, n_dim = num_points, size_pop = 50, max_iter = 500, prob_mut = 1)
best_points, best_distance = ga_tsp.run()
我们展示一下结果:
best_distance

画图查看计算出来的路径,还有迭代次数和y的关系:
fig, ax = plt.subplots(1, 2,figsize = (12, 8))
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(ga_tsp.generation_best_Y)
plt.show()

3.4 使用遗传算法进行曲线拟合
构建数据集:
import numpy as np
import matplotlib.pyplot as plt
from sko.GA import GA
x_true = np.linspace(-1.2, 1.2, 30)
y_true = x_true ** 3 - x_true + 0.4 * np.random.rand(30)
plt.plot(x_true, y_true, 'o')
构建的数据是y=x3−x+0.4y=x^3-x+0.4y=x3−x+0.4,然后加上了随机扰动项。如图:

定义需要拟合的函数(三次函数),然后将残差作为目标函数去求解:
def f_fun(x, a, b, c, d):return a * x ** 3 + b * x ** 2 + c * x + d #三次函数def obj_fun(p):a, b, c, d = presiduals = np.square(f_fun(x_true, a, b, c, d) - y_true).sum()return residuals
求解:
ga = GA(func = obj_fun, n_dim = 4, size_pop = 100, max_iter = 500, lb = [-2] * 4, ub = [2] * 4)
best_params, residuals = ga.run()
print('best_x:', best_params, '\n', 'best_y:', residuals)

可以看到拟合出来的方程为y=0.9656x3−0.0065x2−1.0162x+0.2162y=0.9656x^{3}-0.0065x^{2}-1.0162x+0.2162y=0.9656x3−0.0065x2−1.0162x+0.2162
画出拟合线:
y_predict = f_fun(x_true, *best_params)
fig, ax = plt.subplots()
ax.plot(x_true, y_true, 'o')
ax.plot(x_true, y_predict, '-')
plt.show()

相关文章:

Python优化算法—遗传算法
Python优化算法—遗传算法一、前言二、安装三、遗传算法3.1 自定义函数3.2 遗传算法进行整数规划3.3 遗传算法用于旅行商问题3.4 使用遗传算法进行曲线拟合一、前言 优化算法,尤其是启发式的仿生智能算法在最近很火,它适用于解决管理学,运筹…...
的应用价值剖析)
数据埋点(Data buried point)的应用价值剖析
一、什么是数据埋点?数据埋点指在应用中特定的流程中收集一些信息,用来跟踪应用使用的状况,后续用来进一步优化产品或是提供运营的数据支撑。比如访问数(Visits),访客数(Visitor),停…...

一文弄懂硬链接、软链接、复制的区别
复制 命令:cp file1 file2 作用:实现对file1的一个拷贝。 限制:可以跨分区,文件夹有效。 效果:修改file1,对file2无影响;修改file2,对file1无影响。删除file1,对file…...
界面组件Telerik ThemeBuilder R1 2023开创应用主题研发新方式!
Telerik DevCraft包含一个完整的产品栈来构建您下一个Web、移动和桌面应用程序。它使用HTML和每个.NET平台的UI库,加快开发速度。Telerik DevCraft提供最完整的工具箱,用于构建现代和面向未来的业务应用程序,目前提供UI for ASP.NET包含一个完…...

在FederatedScope 如何查看clientserver之间的传递的参数大小(通讯量)? 对源码的探索记录
在FederatedScope 如何查看client/server之间的传递的参数大小(通讯量)? 对源码的探索记录 背景需求 想给自己的论文补一个通讯开销对比实验:需要计算出client和server之间传递的信息(例如,模型权重、embedding)总共…...

2023爱分析 · 数据科学与机器学习平台厂商全景报告 | 爱分析报告
报告编委 黄勇 爱分析合伙人&首席分析师 孟晨静 爱分析分析师 目录 1. 研究范围定义 2. 厂商全景地图 3. 市场分析与厂商评估 4. 入选厂商列表 1. 研究范围定义 研究范围 经济新常态下,如何对海量数据进行分析挖掘以支撑敏捷决策、适应市场的快…...

20230215_数据库过程_高质量发展
高质量发展 —一、运营结果 SQL_STRING:‘delete shzc.np_rec_lnpdb a where exists (select * from tbcs.v_np_rec_lnpdbbcv t where a.telnumt.telnum and a.outcarriert.OUTCARRIER and a.incarriert.INCARRIER and a.owncarriert.OWNCARRIER and a.starttimet.STARTTIME …...

【百度 JavaScript API v3.0】LocalSearch 位置检索、Autocomplete 结果提示
地名检索移动到指定坐标 需求 在输入框中搜索,在下拉列表中浮动,右侧出现高亮的列表集。选中之后移动到指定坐标。 技术点 官网地址: JavaScript API - 快速入门 | 百度地图API SDK 开发文档:百度地图JSAPI 3.0类参考 实现 …...

运用Facebook投放,如何制定有效的竞价策略?
广告投放中,我们经常会遇到一个问题,就是不知道什么样的广告适合自己的业务。其实,最简单的方法就是根据我们业务本身进行定位并进行投放。当你了解了广告主所处行业及目标受众后,接下来会针对目标市场进行搜索和定位(…...

大数据框架之Hadoop:HDFS(五)NameNode和SecondaryNameNode(面试开发重点)
5.1NN和2NN工作机制 5.1.1思考:NameNode中的元数据是存储在哪里的? 首先,我们做个假设,如果存储在NameNode节点的磁盘中,因为经常需要进行随机访问,还有响应客户请求,必然是效率过低。因此&am…...

计算机网络 - 1. 体系结构
目录概念、功能、组成、分类概念功能组成分类分层结构概念总结OSI 七层模型应用层表示层会话层传输层网络层数据链路层物理层TCP/IP 四层模型OSI 与 TCP/IP 相同点OSI 与 TCP/IP 不同点为什么 TCP/IP 去除了表示层和会话层五层参考模型概念、功能、组成、分类 概念 …...

银行业上云进行时,OLAP 云服务如何解决传统数仓之痛?
本文节选自《中国金融科技发展概览:创新与应用前沿》,从某国有大行构建大数据云平台的实践出发,解读了 OLAP 云服务如何助力银行实现技术平台化、组件化和云服务化,降低技术应用门槛,赋能业务创新。此外,本…...

特定领域知识图谱融合方案:文本匹配算法之预训练Simbert、ERNIE-Gram单塔模型等诸多模型【三】
特定领域知识图谱融合方案:文本匹配算法之预训练模型SimBert、ERNIE-Gram 文本匹配任务在自然语言处理中是非常重要的基础任务之一,一般研究两段文本之间的关系。有很多应用场景;如信息检索、问答系统、智能对话、文本鉴别、智能推荐、文本数据去重、文本相似度计算、自然语…...

【2023最新教程】从0到1开发自动化测试框架(0基础也能看懂)
一、序言 随着项目版本的快速迭代、APP测试有以下几个特点: 首先,功能点多且细,测试工作量大,容易遗漏;其次,代码模块常改动,回归测试很频繁,测试重复低效;最后&#x…...

linux备份命令小记 —— 筑梦之路
Linux dump命令用于备份文件系统。 dump为备份工具程序,可将目录或整个文件系统备份至指定的设备,或备份成一个大文件。 dump命令只可以备份ext2/3/4格式的文件系统, centos7默认未安装dump命令,可以使用yum install -y dump安…...
配置环境变量和打包时区分开发、测试、生产环境)
vue项目(vue-cli)配置环境变量和打包时区分开发、测试、生产环境
1.打包时区分不同环境在自定义配置Vue-cli 的过程中,想分别通过.env.development .env.test .env.production 来代表开发、测试、生产环境。NODE_ENVdevelopment NODE_ENVtest NODE_ENVproduction本来想使用上面三种配置来区分三个环境,但是发现使用test…...

Python 命名规范
Python 命名规范 基本规范 类型公有内部备注Packagepackage_namenone全小写下划线式驼峰Modulemodule_name_module_name全小写下划线式驼峰ClassClassName_ClassName首字母大写式驼峰Methodmethod_nameprotected: _method_name private: __method_name全小写下划线式驼峰Exce…...
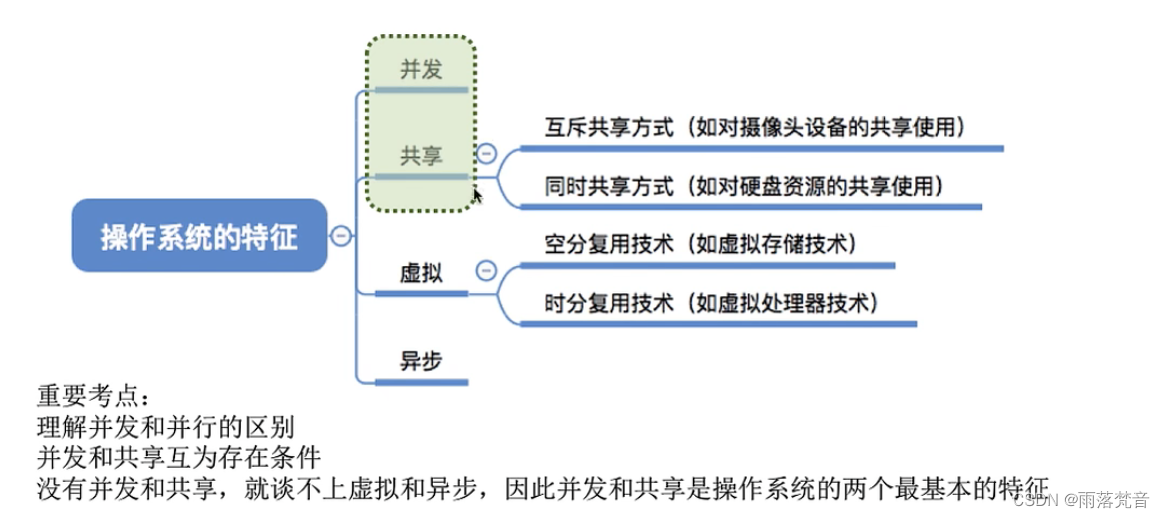
操作系统——2.操作系统的特征
这篇文章,我们来讲一讲操作系统的特征 目录 1.概述 2.并发 2.1并发概念 2.1.1操作系统的并发性 3.共享 3.1共享的概念 3.2共享的方式 4.并发和共享的关系 5.虚拟 5.1虚拟的概念 5.2虚拟小结 6.异步 6.1异步概念 7.小结 1.概述 上一篇文章,我们…...
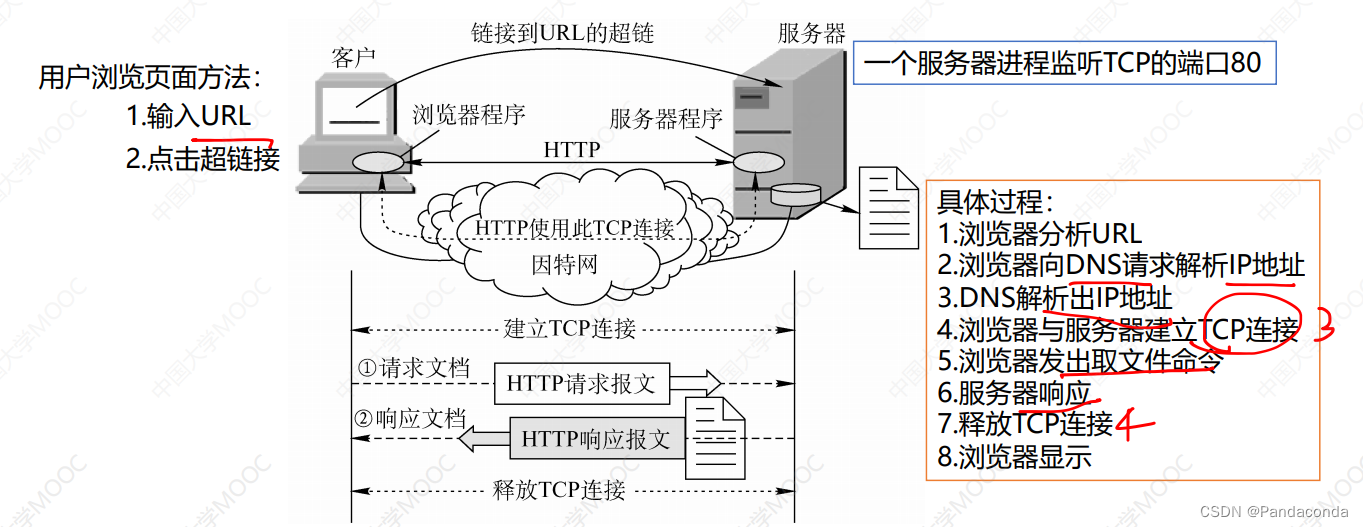
【计算机网络期末复习】第六章 应用层
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📣专栏定位:为想复习学校计算机网络课程的同学提供重点大纲,帮助大家渡过期末考~ 📚专栏地址:https://blog.csdn.net/Newin2020/arti…...

TypeScript基本教程
TS是JS的超集,所以JS基础的类型都包含在内 起步安装 npm install typescript -g运行tsc 文件名 基础类型 Boolean、Number、String、null、undefined 以及 ES6 的 Symbol 和 ES10 的 BigInt。 1 字符串类型 字符串是使用string定义的 let a: string 123 //普…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
