[SCTF2019]babyre 题解
对未来的真正慷慨,是把一切献给现在。
——加缪
目录
1.查壳
2.处理花指令,找到main函数
这一操作过程可以参考下面的视频:
3.静态分析第一部分,psword1
4.静态分析第二部分,psword2
5.静态分析第五部分,psword3
6.根据psword1~3整理出flag
1.查壳
64bit可执行文件
2.处理花指令,找到main函数
操作讲解(讲解后配有这一步骤的视屏)
我们在函数窗口找不到main函数,可能存在一些脏字节之类的东西导致main函数反编译失败
先打开string窗口,跟踪找一下main函数的位置+
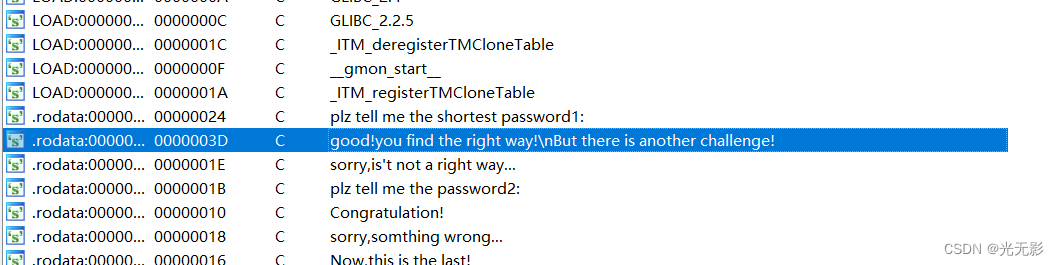
发现一个可疑的字符串
跟进,按下X交叉引用

跟进找到引用这个字符串的函数
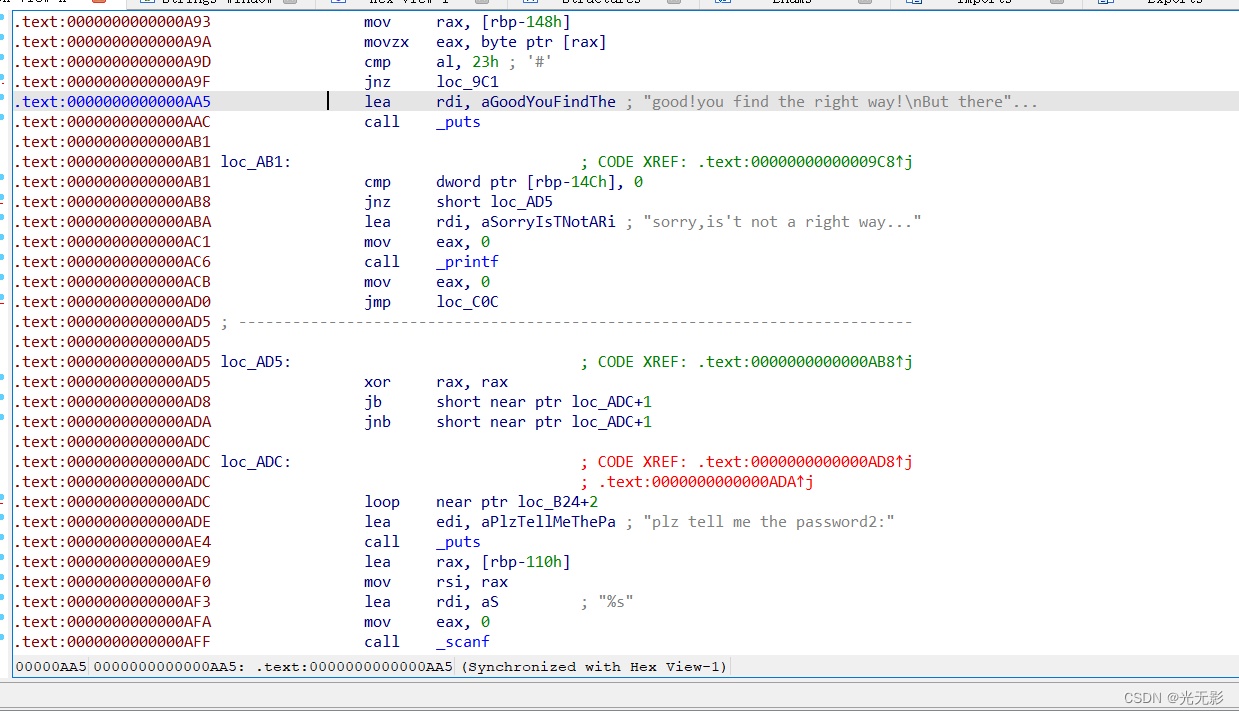 发现代码标红了
发现代码标红了
有一些花指令,nop掉,nop的方法如下:
选中花指令 Edit -> Patch program -> Assemble

花指令的位置:
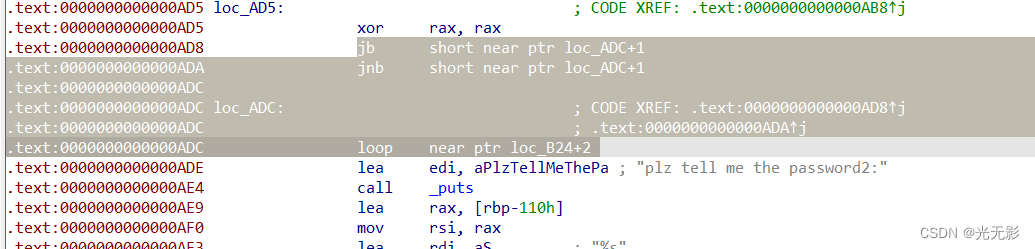
第一处,nop掉

第二处花指令,nop掉

第三处花指令,nop掉

第四处花指令,nop掉
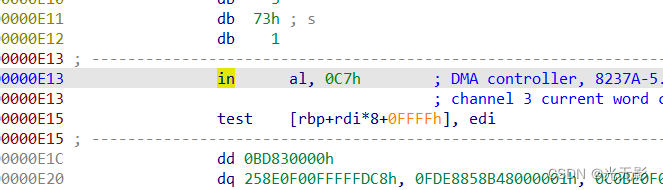
光标点在nop上面,按下如下过程点击

光标移到in处,Edit -> Patch program -> change byte查看字节码,很可能E4是个脏字节,影响了C7(mov)指令的反汇编

我们把E4改为90(90对应的操作码就是nop)
然将这里的数据选中,按下快捷键C重新分析
之后我们选中从push到return的标红的区间按下快捷键P,将其识别为一个函数
注意这一段标红区域有两个retn,有两个函数,要分开来P
这一操作过程可以参考下面的视频:
nop花指令
进过上述操作,我们就得到了main函数和另一个函数
3.静态分析第一部分,psword1
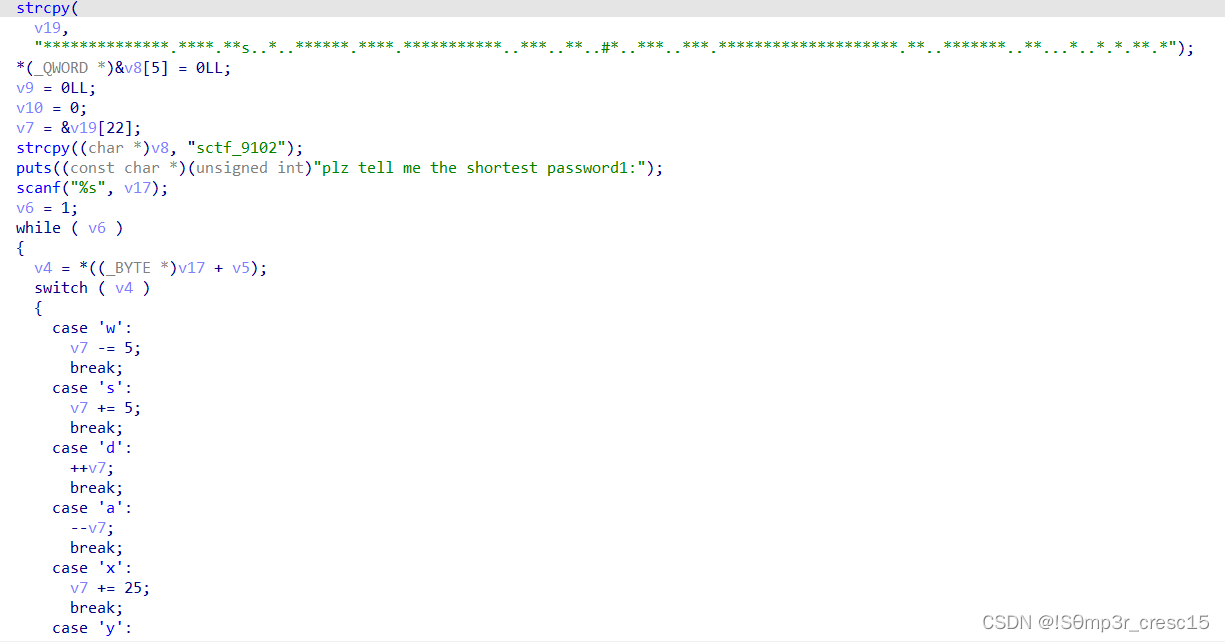
我们看到了一个迷宫图案和移动操作
这又是一个迷宫题
但是有六个移动键,有可能是一个立体迷宫

根据这里的数值判断,这可能是一个5×5×5的迷宫
将字符串排列成迷宫:

走迷宫得到的路径是ddwwxxssxaxwwaasasyywwdd
4.静态分析第二部分,psword2
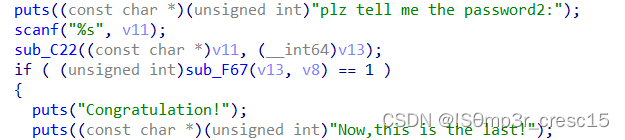
可以看出password2的关键操作函数是sub_C22,且第一个参数就是出入的psword2
跟进查看
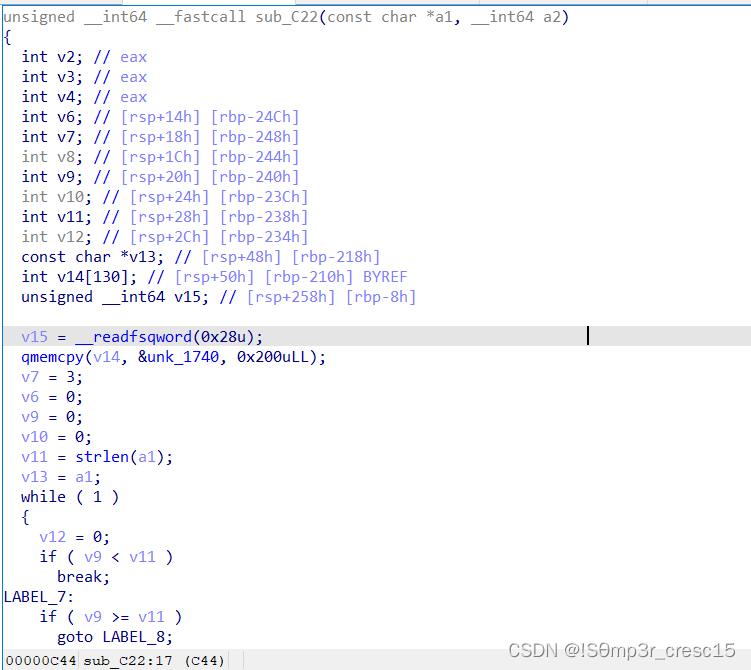
根据这段代码编写wp
#include <stdio.h>
unsigned int data[128] = {0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F,0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F,0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F,0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F,0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F,0x7F, 0x7F, 0x7F, 0x3E, 0x7F, 0x7F, 0x7F, 0x3F,0x34, 0x35, 0x36, 0x37, 0x38, 0x39, 0x3A, 0x3B,0x3C, 0x3D, 0x7F, 0x7F, 0x7F, 0x40, 0x7F, 0x7F,0x7F, 0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06,0x07, 0x08, 0x09, 0x0A, 0x0B, 0x0C, 0x0D, 0x0E,0x0F, 0x10, 0x11, 0x12, 0x13, 0x14, 0x15, 0x16,0x17, 0x18, 0x19, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F,0x7F, 0x1A, 0x1B, 0x1C, 0x1D, 0x1E, 0x1F, 0x20,0x21, 0x22, 0x23, 0x24, 0x25, 0x26, 0x27, 0x28,0x29, 0x2A, 0x2B, 0x2C, 0x2D, 0x2E, 0x2F, 0x30,0x31, 0x32, 0x33, 0x7F, 0x7F, 0x7F, 0x7F, 0x7F
};
int main()
{int ctf[3] = { 0x736374,0x665f39,0x313032 };int i0, i1, i2, i3, i4, i5;for (i0 = 0; i0 < 3; i0++){for(i1=32;i1<128;i1++)for (i2 = 32; i2 < 128; i2++)for (i3 = 32; i3 < 128; i3++)for (i4 = 32; i4 < 128; i4++){i5 = (((((data[i1] << 6) | data[i2]) << 6) | data[i3]) << 6) | data[i4];if (i5 == ctf[i0])printf("%c%c%c%c",i1, i2, i3, i4);}}return 0;
}psword2:c2N0Zl85MS=yMT=yMTAy
5.静态分析第五部分,psword3
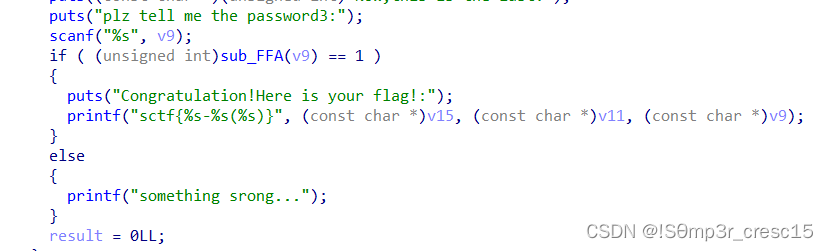
sub_FFA()函数是关键处理函数,跟进

跟进加密函数sub_143B()

继续跟进
编写wp:
#include <stdio.h>
#include "defs.h"
unsigned int ROR4(unsigned int x, int y)
{return (x << (32 - y) | x >> y) & 0xffffffff;
}unsigned int ROL4(unsigned int x, int y)
{return (x >> (32 - y) | x << y) & 0xffffffff;
}__int64 sub_1464(unsigned int a1)
{int v2;unsigned int v3[288] = {0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7,0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05,0x2B, 0x67, 0x9A, 0x76, 0x2A, 0xBE, 0x04, 0xC3,0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99,0x9C, 0x42, 0x50, 0xF4, 0x91, 0xEF, 0x98, 0x7A,0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62,0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08, 0xE8, 0x95,0x80, 0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6,0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA,0x83, 0x59, 0x3C, 0x19, 0xE6, 0x85, 0x4F, 0xA8,0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B,0xF8, 0xEB, 0x0F, 0x4B, 0x70, 0x56, 0x9D, 0x35,0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2,0x25, 0x22, 0x7C, 0x3B, 0x01, 0x21, 0x78, 0x87,0xD4, 0x00, 0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52,0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4, 0xC8, 0x9E,0xEA, 0xBF, 0x8A, 0xD2, 0x40, 0xC7, 0x38, 0xB5,0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1,0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55,0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3,0x1D, 0xF6, 0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60,0xC0, 0x29, 0x23, 0xAB, 0x0D, 0x53, 0x4E, 0x6F,0xD5, 0xDB, 0x37, 0x45, 0xDE, 0xFD, 0x8E, 0x2F,0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C, 0x5B, 0x51,0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD, 0xBC, 0x7F,0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8,0x0A, 0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD,0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0,0x89, 0x69, 0x97, 0x4A, 0x0C, 0x96, 0x77, 0x7E,0x65, 0xB9, 0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84,0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D, 0x20,0x79, 0xEE, 0x5F, 0x3E, 0xD7, 0xCB, 0x39, 0x48,0xC6, 0xBA, 0xB1, 0xA3, 0x50, 0x33, 0xAA, 0x56,0x97, 0x91, 0x7D, 0x67, 0xDC, 0x22, 0x70, 0xB2,0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00,0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00};v2 = (v3[BYTE2(a1)] << 16) | v3[(unsigned __int8)a1] | (v3[BYTE1(a1)] << 8) | (v3[HIBYTE(a1) ] << 24);return ROL4(v2, 12) ^ (unsigned int)(ROL4(v2, 8) ^ ROR4(v2, 2)) ^ ROR4(v2, 6);
}int main()
{ int n = 25;unsigned int v10[30] = { 0 };v10[26] = 0xBE040680;v10[27] = 0xC5AF7647;v10[28] = 0x9FCC401F;v10[29] = 0xD8BF92EF;do{v10[n] =v10[n + 4] ^ sub_1464(v10[n + 1] ^ v10[n + 2] ^ v10[n + 3]);--n;} while (n >= 0);for (int i = 0; i < 4; i++)printf("%c%c%c%c", ((char*)&v10[i])[0], ((char*)&v10[i])[1], ((char*)&v10[i])[2], ((char*)&v10[i])[3]);return 0;
}psword3:fl4g_is_s0_ug1y!
6.根据psword1~3整理出flag
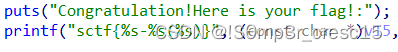
可以知道flag的格式为sctf{%s-%s(%s)}
flag{ddwwxxssxaxwwaasasyywwdd-c2N0Zl85MTAy(fl4g_is_s0_ug1y!)}
相关文章:
[SCTF2019]babyre 题解
对未来的真正慷慨,是把一切献给现在。 ——加缪 目录 1.查壳 2.处理花指令,找到main函数 这一操作过程可以参考下面的视频: 3.静态分析第一部分,psword1 4.静态分析第二部分,psword2 5.静态分析第五部分,psword3 6.根据ps…...

全志H3系统移植 | 移植主线最新uboot 2023.04和kernel 6.1.11到Nanopi NEO开发板
文章目录 环境说明uboot移植kernel移植rootfs移植测试环境说明 OS:Ubuntu 20.04.5 LTSGCC:arm-none-linux-gnueabihf-gcc 10.3.0编译器下载地址:Downloads | GNU-A Downloads – Arm Developer uboot移植 当前最新版本v2023.04-rc2下载地址:https://github.com/u-boot/u-…...

vue项目第四天
使用elementui tabplane组件实现历史访问记录组件的二次封装<el-tabs type"border-card"><el-tab-pane label"用户管理">用户管理</el-tab-pane><el-tab-pane label"配置管理">配置管理</el-tab-pane><el-tab-…...
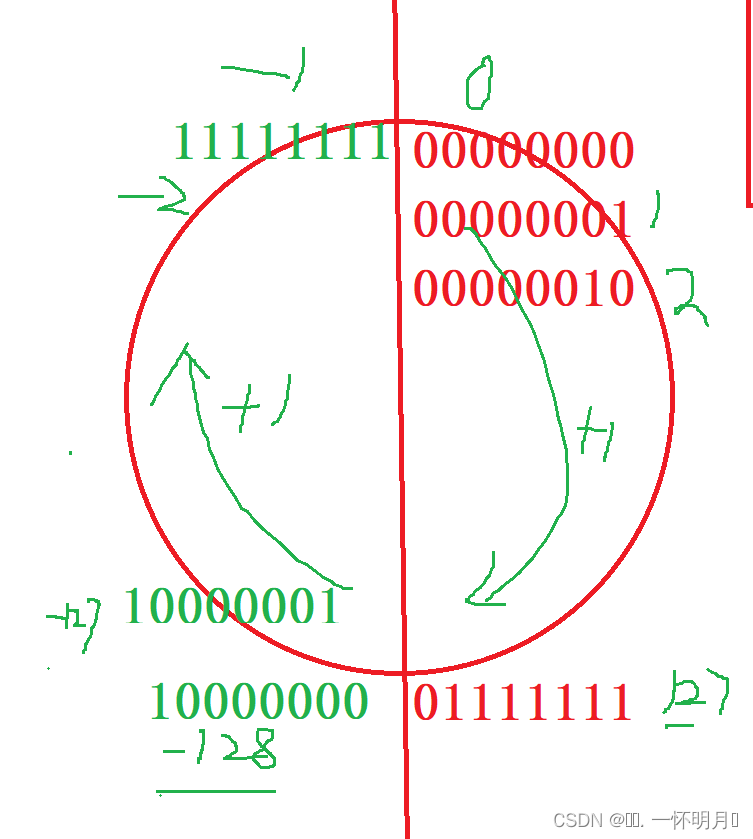
「C语言进阶」数据内存的存储
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰数据类型的介绍 🐰类型的意义 🐰数据类型的基本归类…...

面试必问:进程和线程的区别(从操作系统层次理解)
1.什么是进程?为什么要有进程? 进程有一个相当精简的解释:进程是对操作系统上正在运行程序的一个抽象。 这个概念确实挺抽象,仔细想想却也挺精准。 我们平常使用计算机,都会在同一时间做许多事,比如边看…...

ModuleNotFoundError: No module named ‘apex‘与 error: legacy-install-failure
ModuleNotFoundError: No module named ‘apex’ ModuleNotFoundError: No module named apex 表示 Python 在搜索模块时无法找到名为 apex 的模块。这通常是因为您没有安装 apex 模块或安装不正确。 apex 是一个针对混合精度训练和优化的 PyTorch 扩展库,您可以通过…...
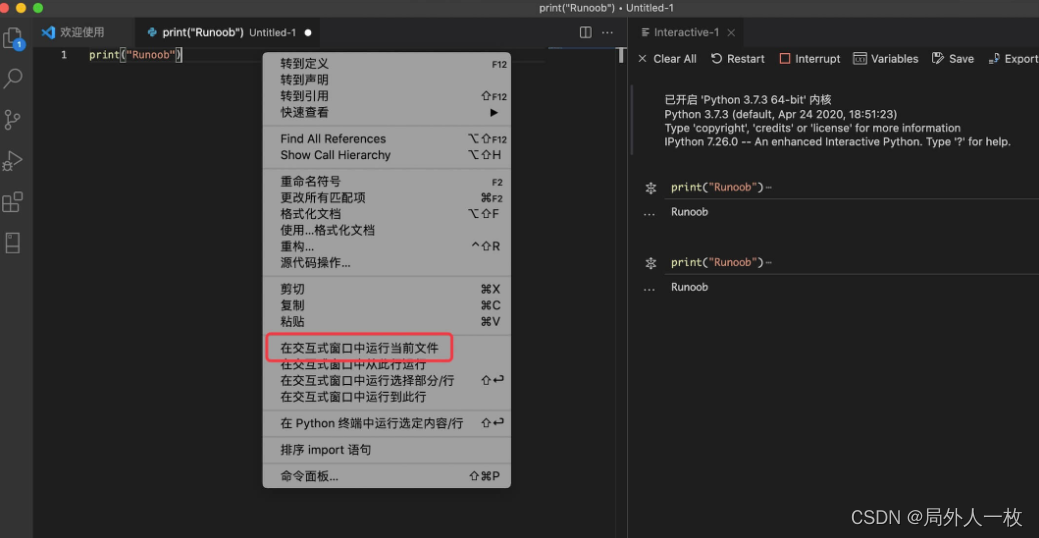
Python3 VScode 配置
Python3 VScode 配置 在上一章节中我们已经安装了 Python 的环境,本章节我们将介绍 Python VScode 的配置。 准备工作: 安装 VS Code 安装 VS Code Python 扩展 安装 Python 3 安装 VS Code VSCode(全称:Visual Studio Code&…...

VMware 修复了三个身份认证绕过漏洞
Bleeping Computer 网站披露,VMware 近期发布了安全更新,以解决 Workspace ONE Assist 解决方案中的三个严重漏洞,分别追踪为 CVE-2022-31685(认证绕过)、CVE-2022-31686 (认证方法失败)和 CVE-…...

实现一个简单的Database10(译文)
GreatSQL社区原创内容未经授权不得随意使用,转载请联系小编并注明来源。GreatSQL是MySQL的国产分支版本,使用上与MySQL一致。作者: 花家舍文章来源:GreatSQL社区原创 前文回顾 实现一个简单的Database系列 译注:csta…...
CTF-取证题目解析-提供环境
一、安装 官网下载:Volatility 2.6 Release 1、将windows下载的volatility上传到 kali/home 文件夹里面 3、将home/kali/vol刚刚上传的 移动到use/sbin目录里面 mv volatility usr/local/sbin/ 切换到里面 cd /usr/local/sbin/volatility 输入配置环境echo $PAT…...

计算机基础 | 网络篇 | TCP/IP 四层模型
前沿:撰写博客的目的是为了再刷时回顾和进一步完善,其次才是以教为学,所以如果有些博客写的较简陋,是为了保持进度不得已而为之,还请大家多多见谅。 一、OSI 七层模型 参考文章:OSI 和 TCP/IP 网络分层模型…...

实时数据仓库
1 为什么选择kafka? ① 实时写入,实时读取 ② 消息队列适合,其他数据库受不了 2 ods层 1)存储原始数据 埋点的行为数据 (topic :ods_base_log) 业务数据 (topic :ods_base_db) 2)业务数据的有序性&#x…...

leetcode 1250. 检查「好数组」
给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。 假如该和结果为 1,那么原数组就是一个「好数组」,则返回 True;否则请返回 False。 示例 1&…...

JDK动态代理和CGLib动态代理的区别
原文网址:JDK动态代理和CGLib动态代理的区别_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Java中JDK动态代理和CGLib动态代理的区别。 区别概述 项 JDK动态代理 CGLIB动态代理 接口是否需实现 只能代理实现了接口的类。 可以代理没有实现接口的类。 原理 继承…...

Leetcode.1250 检查「好数组」
题目链接 Leetcode.1250 检查「好数组」 Rating : 1983 题目描述 给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。 假如该和结果为 1,那么原数组就是一个「…...

WMS系统推荐,如何选到适合企业的仓库管理系统
市场上有很多WMS系统,但是现在很多仓库管理系统都在使用WMS系统。那么在选择WMS系统时应该考虑什么呢?明确业务发展特征,准确表达能力目标许多物流企业在选择物流管理系统时,往往会被物流管理系统的整体系统所迷惑,在功…...
C语言的期末复习
🌈博客主页:卿云阁 💌欢迎关注🎉点赞👍收藏⭐️留言📝 🌟本文由卿云阁原创! 🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢&a…...

强化学习之DQN论文介绍
强化学习之DQN论文介绍DQN摘要介绍问题特点经验回放相关工作实验算法流程结论DQN 摘要 1.基于Q-learning从高维输入学习到控制策略的卷积神经网络。 2.输入是像素,输出是奖励函数。 3.主要训练、学习Atari 2600游戏,在6款游戏中3款超越人类专家。 介绍 …...

使用luaBridge添加自己的C++脚本插件能力
概述 如果我们有一个应用需要频繁的更改业务逻辑,但是基础功能不变,那么我们可以将基础功能作为底层接口,上层的功能按照脚本方式来编写。很多插件都这样的原理,比如我们的浏览器的JS就这样,小程序也是这样的原理,我们使用C++也很容易实现这样的功能。 lua是最小最精致的…...

再拾起博客
一切要从去年12月27日被裁员的那天说起。 那天是星期二,和平常一样,8点20的闹钟响起,但我习惯性的磨蹭到8点40起床,洗漱完成后9点过几分出门,骑车20多分钟几乎是踩点到的公司,正当我坐在工位准备平复心情切…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

