AcWing 840. 模拟散列表
题目描述
餐前小菜:
在讨论本题目之前先看一个简单的问题:给出 NNN 个正整数 (a1,a2,...,an)(a_1,a_2,...,a_n)(a1,a2,...,an),再给出 MMM 个正整数 (x1,x2,...,xm)(x_1,x_2,...,x_m)(x1,x2,...,xm),问这 MMM 个数中的每个数是否在 NNN 个数中出现过,其中 N,M≤105N,M ≤ 10^5N,M≤105,且所有正整数均不超过 10510^5105。比较容易想到的思路是:对每个欲查询的数 xix_ixi,遍历 NNN 看看是否存在。该算法时间复杂度为 O(NM)O(NM)O(NM),是有很多的优化空间的。
经典思想为用空间换时间,设有一个 hashTable[N],其中 hashTable[xix_ixi] == true 表示正整数 xix_ixi 在 NNN 个正整数 (a1,a2,...,an)(a_1,a_2,...,a_n)(a1,a2,...,an) 中找到了与之相等的数,若为 false 表示没有出现过。我们该怎么做呢?初始时 hashTable 全为 false,对读入的 NNN 个数 (a1,a2,...,an)(a_1,a_2,...,a_n)(a1,a2,...,an),进行预处理将 hashTable[aia_iai] 设置为 true,接着对 MMM 个欲查正整数,直接查看 hashTable[xix_ixi] 为 true/false 来判断出现/没出现过。在许多算法里都用到了这样一种方案:把输入的数作为数组下标来进行查询。将查询的时间复杂度降低至 O(1)O(1)O(1)。
分析:
但注意本题中,我们每个数的范围是 [−109,109][-10^9,10^9][−109,109] 这是没有办法作为数组下标进行查询的!因此我们希望能将一些不合适的下标(负数或过大)转换为我们期望的一个范围内。
因此我们引入哈希(散列、hash)的思想,将元素(element, e)通过一个函数转换为整数,使得该整数可以尽量地代表这个元素。该函数称为哈希函数 h()h()h()。即对 eee,求 h(e)h(e)h(e)。
看看这道题 −109≤e≤109-10^9≤e≤10^9−109≤e≤109 为整数,可以使用哪些常用的哈希函数呢?
- 直接定址法(简单,常用于映射要求不高的题目): h(e)=eh(e)=eh(e)=e。餐前小菜中对于需要查找的 xix_ixi,其实就是使用了该方案,有一个隐式的h(xi)=xih(x_i)=x_ih(xi)=xi,将要查询的数作为数组下标。
- 平方取中法(基本不使用该方法,可忽略):将 eee 的平方的中间若干位作为 hash 值。
- 除留余数法(重要,常用):h(e)=eh(e)=eh(e)=e modmodmod kkk。通过该哈希函数,可以把很大的数转换为一个不超过 kkk 的数,这样就可以作为可行的数组下标。这里 TableSize(即可 hash 映射的总长度必须大于等于 kkk,不然会产生越界),当 kkk 是一个素数时,h(e)h(e)h(e) 能尽可能覆盖 [0,k)[0,k)[0,k) 范围内的每一个数。这里将 TableSize与 kkk 都设置为相同的素数。但本题远没有这么简单,有两点需要注意:
① e 的取值可能为负,在人类世界里负数的模有各种各样的计算方法,但总归会得到一个在现有规则下“正确的”一个非负数解,同理根据高级程序语言的不同计算的方式也不同,但结果却不尽相同,在C/C++中,若对负数求模运算,会得到一个负的解,这显然是与模运算的定义所违背的,因此需要对运算结果进行加工:ans = (e % TableSize + TableSize) % TableSize,这样不论是正数还是负数都能得到正确的解,具体的细节不多做解释,可以将它看作是与加减乘除相类似的算法。
② TableSize 该如何选取呢?这是很重要的一点,同时也决定了哈希函数(与 k 有关)的设计。按照上文分析, TableSize 又应该大于等于输入总数 NNN 的质数且根据上文需要大于等于 kkk,而 k 应为一个质数,我们得到一下关系:TableSize=k≥NTableSize=k≥NTableSize=k≥N,而 NNN 不是质数,因此不使用它,我们可以使用比 NNN 大的第一个质数。// 求比 N 大的第一个质数 N = 100000 for (int i = N; ; i ++) {bool flag = false;for (int j = 2; j * j <= i; j ++){if (i % j == 0){flag = true;break;}}if (flag){cout << i << endl;break;} }>_: 100003
以我们对求余运算的了解,对于两不同的数 e1,e2e_1,e_2e1,e2,他们的 hash值可能是相同的,当 e1e_1e1 将表中下标为 h(e1)h(e_1)h(e1) 的单元占据时,e2e_2e2 便不能再使用这个位置了,此时发生了冲突。
为解决冲突,将介绍一下三种方法,其中第一、二种都计算了新的 hash 值,又称为开放寻址法:
- 线性探测法(Linear Probing):当得到 eee 的 hash值h(e)hash值 h(e)hash值h(e) 后,观察到 hashTable 中下标为 h(e)h(e)h(e) 的位置已经被其他元素占用,那么就检查下个位置 h(e)+1h(e)+1h(e)+1 是否被占用,如果没有,就使用这个位置;如果还是被占用就继续向后检查,当检查长度超出 TableSize 时,就回到表头继续向后查找,知道找到能使用的位置或表中所有位置均被使用过为止。这种做法容易扎堆。同时,由于线性探测法有向后检查的特征,因此 hashTable 的设置至少要为 N 的 2 倍,又根据我们在除留余数法中的分析,TableSize 为 200003。而具体实现中,用一个极大值(0x3f3f3f3f)(0x3f3f3f3f)(0x3f3f3f3f)来标识一个位置是否被占用,如被占用,则 hashTable[h(e)]=ehashTable[h(e)] =ehashTable[h(e)]=e,否则 hashTable[h(e)]=0x3f3f3f3fhashTable[h(e)]=0x3f3f3f3fhashTable[h(e)]=0x3f3f3f3f。
- 平方探测法(Quadratic probing):在平方探测法中,为了尽可能避免扎堆现象,当表中 h(e)h(e)h(e) 的位置被占用时,将按下面的顺序检查表中的位置:h(e)+12、h(e)−12、h(e)+22、h(e)−22、h(e)+32...h(e)+1^2、h(e)-1^2、h(e)+2^2、h(e)-2^2、h(e)+3^2...h(e)+12、h(e)−12、h(e)+22、h(e)−22、h(e)+32...。①如果检查过程中 h(e)+i2>TableSizeh(e)+i^2>TableSizeh(e)+i2>TableSize 时(下个位置超出表尾),就把 h(e)+i2h(e)+i^2h(e)+i2 对 TableSize 取模;②如果检查过程中 h(e)−i2<0h(e)-i^2<0h(e)−i2<0时(下个位置超出表头),就将((h(e)−i2)modTableSize+TableSize)modTableSize((h(e)-i^2)modTableSize+TableSize)modTableSize((h(e)−i2)modTableSize+TableSize)modTableSize 作为结果,如果为避免出现负数的麻烦可以只进行正方向的平方探测。有结论证明,如果 eee 在 [0,TableSize][0,TableSize][0,TableSize] 范围内都无法找到位置,当 i≥TableSizei≥TableSizei≥TableSize 时,也一定无法找到位置。
- 链地址法(拉链法):拉链法不计算新的 hash值,而是把所有 h(e)h(e)h(e) 相同的 eee 连接成一条单链表。,若 e1,e2e_1,e_2e1,e2 有相同 hash值,则可以形成这样一个单链表:

可以看到,线性探测法比较直观而拉链法操作比较多,因此对其进行模拟一下,请结合代码理解!

代码(C++)
线性探测法
#include <iostream>using namespace std;// TS: TableSize
const int TS = 200003, null = 0x3f3f3f3f;
int hashtable[TS];// 哈希函数,输入元素返回哈希值用于初步定位 hashtable
// h(e) 返回的是未经线性探测的位置
int h(int e)
{return (e % TS + TS) % TS;
}// find(e) 返回经过线性探测的位置
int find(int e)
{int he = h(e);while (hashtable[he] != null && hashtable[he] != e){he ++;if (he == TS) he = 0;}return he;
}int main()
{int n;cin >> n;// 初始化时,每一位都没有被占用,即没有出现过for (int i = 0; i < TS; i ++) hashtable[i] = null;while (n --){char op;int e;cin >> op >> e;// 找到最终位置后进行插入if (op == 'I') hashtable[find(e)] = e;else{// 通过经过线性探测的位置来判断 e 的性质//而不能通过计算一次哈希函数就去hashtable看if (hashtable[find(e)] == null) cout << "No" << endl;else cout << "Yes" << endl;}}
}
拉链法
#include <iostream>using namespace std;const int TS = 100003;
// TS: TableSize, no: node, ne: next
int hashtable[TS], no[TS], ne[TS], idx;int h(int e)
{// 哈希函数,输入元素返回哈希值用于初步定位 hashtablereturn (e % TS + TS) % TS;
}void insert(int e)
{int he = h(e);no[idx] = e;ne[idx] = hashtable[he];hashtable[he] = idx ++;
}int find(int e)
{int he = h(e);// 通过 hashtable[he] 可以查询到最后一个被连接到 h(e) 位置的元素// 再顺着该元素往前查看,看 e 是否在此链中出现过for (int i = hashtable[he]; i != -1; i = ne[i]){// i 实际上为 idxif (no[i] == e) return true;}return false;
}int main()
{int n;cin >> n;// 每个位置的链没有连接元素for (int i = 0; i < TS; i ++) hashtable[i] = -1;while (n --){char op;int e;cin >> op >> e;if (op == 'I') insert(e);else{if (find(e)) cout << "Yes" << endl;else cout << "No" << endl;}}
}
相关文章:

AcWing 840. 模拟散列表
题目描述 餐前小菜: 在讨论本题目之前先看一个简单的问题:给出 NNN 个正整数 (a1,a2,...,an)(a_1,a_2,...,a_n)(a1,a2,...,an),再给出 MMM 个正整数 (x1,x2,...,xm)(x_1,x_2,...,x_m)(x1,x2,...,xm),问这 MMM 个数中…...

【网络工程】常见HTTP响应状态码
前言 什么是HTTP响应状态码? HTTP状态码(HTTP Status Code)是表示网页服务器超文本传输协议响应状态的3位数字代码 HTTP响应码被分为五大类 信息响应(100~199)成功响应(200~299)重定向响应&am…...
)
Python之ruamel.yaml模块详解(二)
Python之ruamel.yaml模块详解(二)4 将YAML解析为Python对象并修改5 使用旧API将YAML解析为Python对象并修改6 使用[]和.get()访问合并的键:7 使用insert()方法插入内容8 使用yaml.indent()更改默认缩进9 使用yaml.compact()隔行显示10 同一数…...

若依框架 --- 偶发的el-select无法选择的问题
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...

【Linux】tmpfile 使用介绍
tmpfile 使用介绍 1 介绍 很多情况下,需要系统自动识别/tmp、/var/tmp下的临时目录,并将其自动清理其中的过期文件。这个工具就是systemd-tmpfiles。 网上很多博客使用tmpwatchcron的方法来管理临时文件和临时存放文件的目录,在后期的版本…...

实现光线追踪重投影的方法
光线追踪重投影方法 重投影这项技术一般用于时间性帧复用技术上,例如TAA(Temporal Anti-Aliasing)反走样或者抗锯齿技术。读这篇文章最好先对TAA这类技术的算法流程有了解。 1.TAA抗锯齿技术简介 先简单介绍下TAA抗锯齿的原理,在游戏中,当前…...

Hyperbolic Representation Learning for CV
Contents Hyperbolic geometry[CVPR 2020] Hyperbolic visual embedding learning for zero-shot recognitionIntroductionApproachHyperbolic Label Embedding LearningHyperbolic Image Embedding LearningExperiment[CVPR 2020] Hyperbolic Image EmbeddingsIntroduction...
In Context Learning 相关分享
个人知乎详见 https://zhuanlan.zhihu.com/p/603650082/edit 1. 前言 随着大模型(GPT3,Instruction GPT,ChatGPT)的横空出世,如何更高效地提示大模型也成了学术界与工业界的关注,因此In-context learning…...
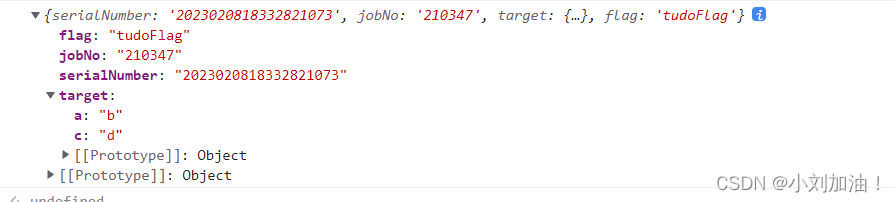
【前端笔试题一】:解析url路径中的query参数
前言 本文记录下在笔试过程中的前端笔试编程题目,会持续更新 1. 题目: 解析 url 路径中的 query 参数,比如:‘http://building/#/skeleton?serialNumber2023020818332821073&jobNo210347&target%7B%22a%22%3A%22b%22%2C…...
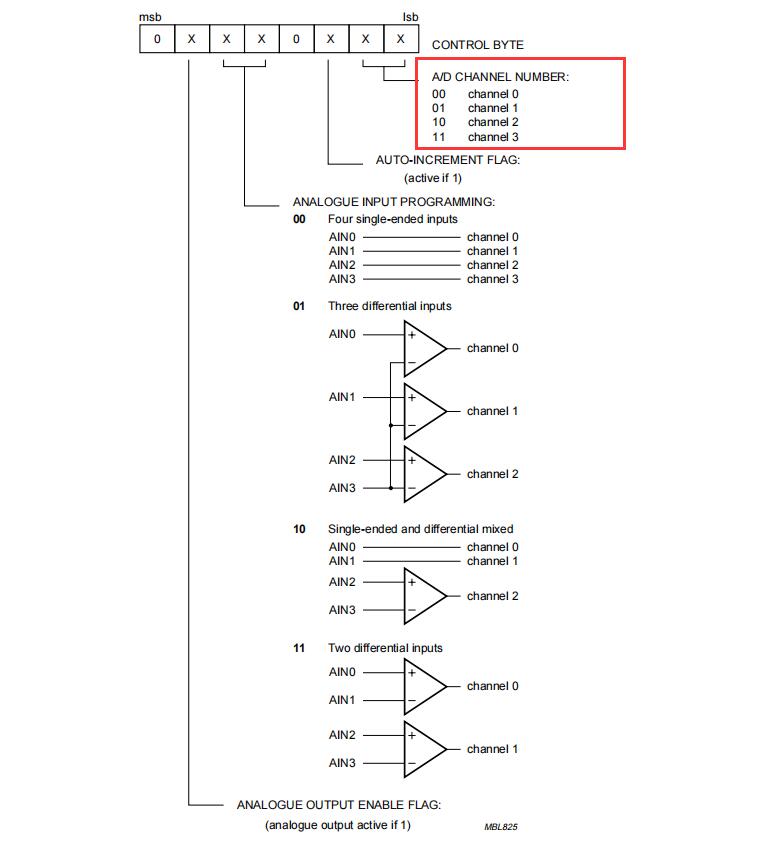
K_A12_001 基于STM32等单片机采集火光火焰传感参数串口与OLED0.96双显示
K_A12_001 基于STM32等单片机采集火光火焰传感参数串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:四、部分代码说明1、接线引脚定义1.1、STC89C52RC火光火焰模块1.2、STM32F103C8T6火光火焰模块五、基础知识学习与相…...
Java基础42 枚举与注解
枚举与注解一、枚举(enumeration)1.1 自定义类实现枚举1.2 enum关键字实现枚举1.2.1 enum的注意事项1.2.2 enum的使用练习1.2.3 enum的常用方法1.2.4 enum的使用细节及注意事项1.2.5 enum练习二、注解(Annotation)2.1 Override&am…...

shell的变量和引用
文章目录二、变量和引用2.1 什么是变量2.2变量的命名2.3 变量的类型2.3.1 根据数据类型分类2.3.2 根据作用域分类2.4 变量的定义2.5 shell中的引用2.6 变量的运算练习:二、变量和引用 在程序设计语言中,变量是一个非常重要的概念。也是初学者在进行Shel…...

基于PHP的招聘网站
摘要在Internet高速发展的今天,我们生活的各个领域都涉及到计算机的应用,其中包括在线招聘的网络应用,在外国在线招聘已经是很普遍的方式,不过国内的在线招聘可能还处于起步阶段。招聘网站具有招聘信息功能的双向选择,…...
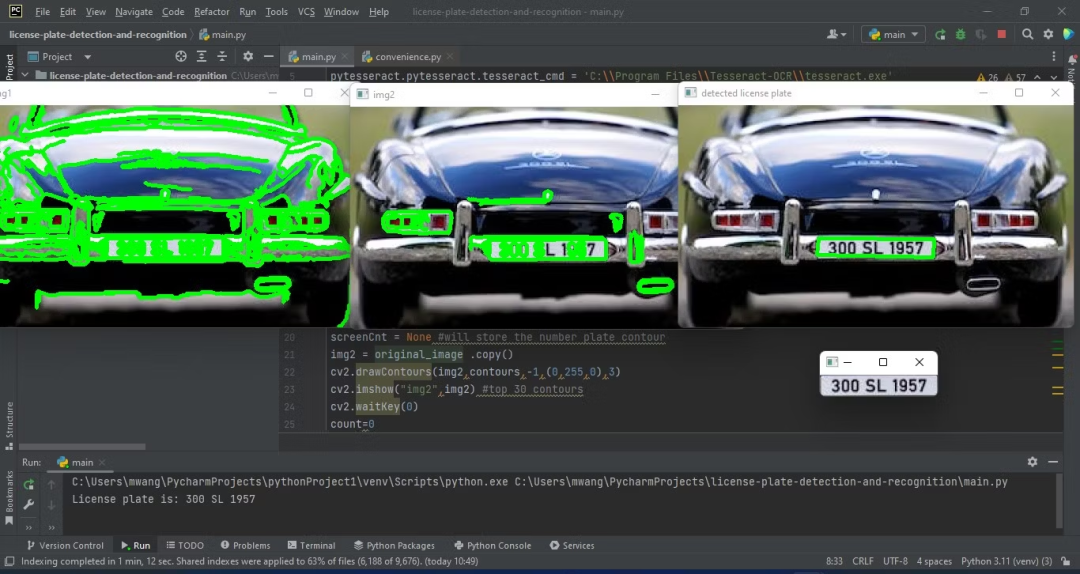
轻松使用 Python 检测和识别车牌(附代码)
车牌检测与识别技术用途广泛,可以用于道路系统、无票停车场、车辆门禁等。这项技术结合了计算机视觉和人工智能。 本文将使用Python创建一个车牌检测和识别程序。该程序对输入图像进行处理,检测和识别车牌,最后显示车牌字符,作为…...
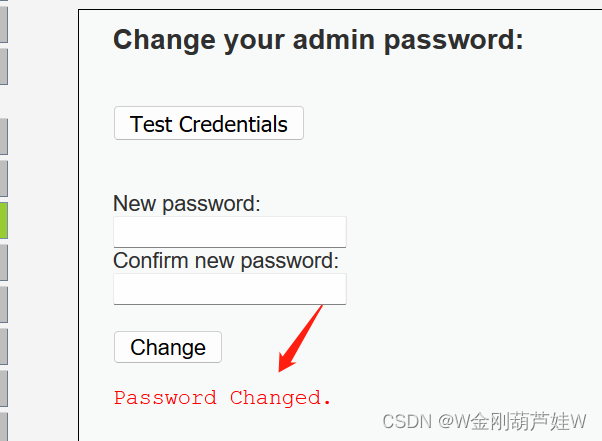
DVWA—CSRF-Medium跨站请求伪造中级
注意: 1、这里对XSS(Stored)关卡不熟悉的可以从这里去看http://t.csdn.cn/ggQDK 2、把难度设置成 Medium 一、这一关同样我们需要埋下伏笔,诱使用户点击来提交,首先从XSS(Stored)入手。 注意:在前面介绍…...
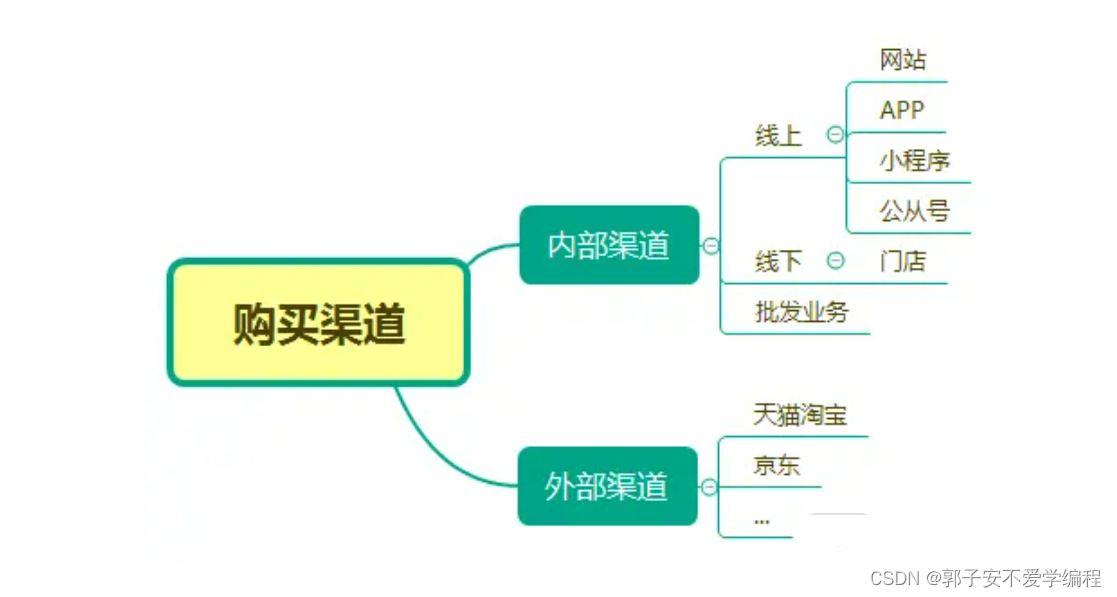
【电商】后台订单生成
结合商品流转的电商系列介绍了一些了,商品已经采购入库、价格税率设置好了、活动及相关模板也已经准备完毕,下面就应该上架销售了,现在接着聊下订单的生成。 订单从产生到最终的关闭需要经历很多的环节,订单也是电商系统的核心数据…...

作为公司,这个5款在线软件工具赶紧安利起来!
2023年了 ,您的企业还没使用在线软件工具吗?自从用了在线工具之后,感觉打开了新办公世界的大门,效率蹭蹭蹭地往上涨啊。对于喜欢追求效率和便捷的我来说,在线实在是太棒了!今天安利几个非常不错的在线软件工…...

面试(七)为什么一般希望将析构函数定义为虚函数
class B { public:~B() // 基类析构函数不为虚函数{cout << "B::~B()" << endl;} };class D : public B { public:~D(){cout << "D::~D()" << endl;} };void Test(B* t) {delete t;t nullptr; }int main() {B *pb new B;Test…...

MySQL必会四大函数-时间函数
一、时间日期获取函数 获取当前日期(date)函数:curdate() mysql> select curdate(); 2023-02-09 获取当前时间(time)函数:curtime() select curtime(); 08:49:27 获取当前时间戳(date &…...
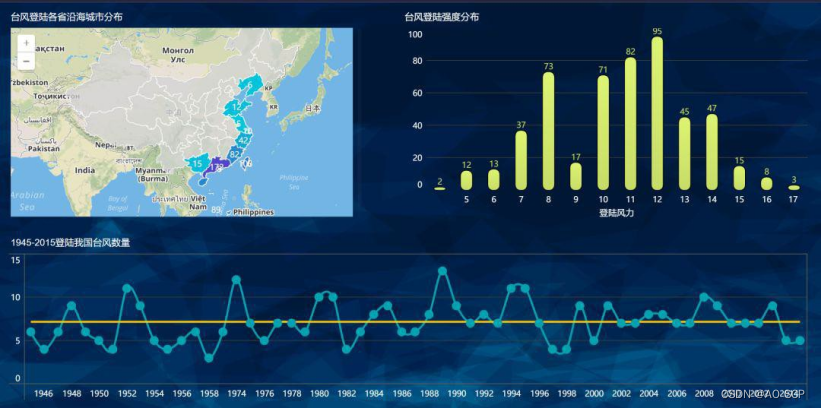
震惊!邻桌的程序猿做可视化报告竟然比我还快,带着好奇心我打开了他的电脑,发现惊天秘密,原因竟是...
其实,本文就是想分享一个做可视化的捷径! 制作可视化的方式有千千万。 Excel 控若能轻车熟路驾驭 VBA,能玩出各种花来,再不济借助图表插件外援也能秒杀一众小白选 手。 会编程的,Echarts 几十行代码,分分…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
