转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录
- 1. 转换矩阵、平移矩阵、旋转矩阵之间的关系
- 2. 缩放变换、平移变换和旋转变换
- 2. python实现旋转矩阵、四元数、欧拉角互相转化
由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄明白之后干脆写一篇文章,给人方便同时于己方便,后续如有扩充或变动也方便添加。
1. 转换矩阵、平移矩阵、旋转矩阵之间的关系
假设有两个向量a1=(x1,y1,z1)a_1 = (x_1, y_1, z_1)a1=(x1,y1,z1)和a2=(x2,y2,z2)a_2 = (x_2, y_2, z_2)a2=(x2,y2,z2),它们的转换关系为:
a1=R∗a2+Ta_1 = R * a_2 + T a1=R∗a2+T
这里RRR就是它的旋转矩阵,TTT就是它的平移矩阵。使用齐次方式表示如下:
(a11)=(RT01)∗(a21)\begin{pmatrix} a_1\\ 1 \end{pmatrix}= \begin{pmatrix} R&T\\ 0&1 \end{pmatrix}* \begin{pmatrix} a_2\\1 \end{pmatrix} (a11)=(R0T1)∗(a21)
使用元素值替换后,表示如下:
(x1y1z11)=(r11r12r13t1r21r22r23t2r31r32r33t30001)∗(x2y3z21)\begin{pmatrix} x_1\\y_1\\z_1\\1 \end{pmatrix}= \begin{pmatrix} r_{11}&r_{12}&r_{13}&t_{1}\\ r_{21}&r_{22}&r_{23}&t_{2}\\ r_{31}&r_{32}&r_{33}&t_{3}\\ 0&0&0&1 \end{pmatrix}* \begin{pmatrix} x_2\\y_3\\z_2\\1 \end{pmatrix} x1y1z11=r11r21r310r12r22r320r13r23r330t1t2t31∗x2y3z21
在仿射变换中的转换矩阵表示先线性变换再平移。在这里转换矩阵表示如下:
转换矩阵=(r11r12r13t1r21r22r23t2r31r32r33t30001)转换矩阵= \begin{pmatrix} r_{11}&r_{12}&r_{13}&t_{1}\\ r_{21}&r_{22}&r_{23}&t_{2}\\ r_{31}&r_{32}&r_{33}&t_{3}\\ 0&0&0&1 \end{pmatrix} 转换矩阵=r11r21r310r12r22r320r13r23r330t1t2t31
平移矩阵表示如下:
平移矩阵T=(t1t2t3)平移矩阵T=\begin{pmatrix} t_{1}\\ t_{2}\\ t_{3}\\ \end{pmatrix} 平移矩阵T=t1t2t3
旋转矩阵表示如下:
旋转矩阵R=(r11r12r13r21r22r23r31r32r33)旋转矩阵R=\begin{pmatrix} r_{11}&r_{12}&r_{13}\\ r_{21}&r_{22}&r_{23}\\ r_{31}&r_{32}&r_{33} \end{pmatrix} 旋转矩阵R=r11r21r31r12r22r32r13r23r33
2. 缩放变换、平移变换和旋转变换
如果理解以上知识点之后,缩放变换、平移变换和旋转变换的特殊情况也迎刃而解。
- 缩放变换
缩放变换只是在尺度上进行改变,所以它的变换形式如下:
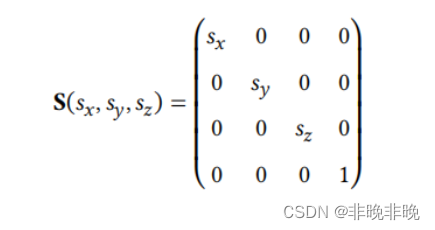
- 平移变换
平移变换的时候,角度不发生改变,也就是旋转矩阵R为单位矩阵,所以它的变换形式如下:
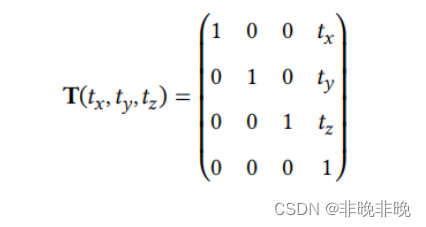
- 旋转变换
当空间内的物体绕着 x 轴,y 轴或者 z 轴旋转的时候,变换矩阵为:

对于一般性的旋转问题,可以用简单的旋转描述复杂的旋转。用 x 轴,y 轴和 z 轴上的旋转来定义旋转:
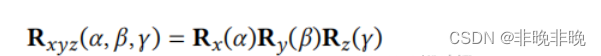
这三个角就被称作欧拉角(Euler angles)。
- 一目了然
- 这个也不错
2. python实现旋转矩阵、四元数、欧拉角互相转化
在应用中,我们往往会遇到旋转矩阵、四元数和欧拉角之间的互相转换,在这里,我们只使用python代码来实现它们之间互相转换。
from scipy.spatial.transform import Rotation as Rdef quaternion2euler(quaternion):r = R.from_quat(quaternion)euler = r.as_euler('xyz', degrees=True)return eulerdef euler2quaternion(euler):r = R.from_euler('xyz', euler, degrees=True)quaternion = r.as_quat()return quaterniondef euler2rotation(euler):r = R.from_euler('xyz', euler, degrees=True)rotation_matrix = r.as_matrix()return rotation_matrixdef quaternion2rotation_matrix(quaternion):r = R.from_quat(quaternion)rotation_matrix = r.as_matrix()return rotation_matrixdef rotation_matrix2euler(rotation_matrix):r = R.from_matrix(rotation_matrix)euler = r.as_euler('xyz', degrees=True)return eulerdef rotation_matrix2quaternion(rotation_matrix):r = R.from_matrix(rotation_matrix)quaternion = r.as_quat()return quaternionif __name__ == '__main__':# 四元数=>欧拉角quaternion = [0.71934025092983234, -1.876085535681999e-06, -3.274841213980097e-08, -0.69465790385533299]euler = quaternion2euler(quaternion) # [-9.20000743e+01 1.52039496e-04 -1.52039496e-04]print(f'euler: {euler}')# 四元数=>旋转矩阵rotation_matrix = quaternion2rotation_matrix(quaternion)print(f'rotation_matrix: {rotation_matrix}')# 欧拉角=>四元数quaternion = euler2quaternion(euler)print(f'quaternion: {quaternion}') # [-7.19340251e-01 1.87608554e-06 3.27484122e-08 6.94657904e-01]# 欧拉角=>旋转矩阵rotation_matrix = euler2rotation(euler)print(f'rotation_matrix: {rotation_matrix}')# 旋转矩阵=>欧拉角euler = rotation_matrix2euler(rotation_matrix)print(f'euler: {euler}')# 旋转矩阵=>四元数quaternion = rotation_matrix2quaternion(rotation_matrix)print(f'quaternion: {quaternion}')
相关文章:
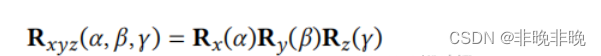
转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录1. 转换矩阵、平移矩阵、旋转矩阵之间的关系2. 缩放变换、平移变换和旋转变换2. python实现旋转矩阵、四元数、欧拉角互相转化由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄…...
中国地图航线图(echarjs)
1、以上为效果图 需要jq、echarjs、china.json三个文件支持。以上 2、具体代码 DOM部分 <!-- 服务范围 GO--> <div class"m-maps"><div id"main" style"width:1400px;height: 800px; margin: 0 auto;"> </div> <!-…...
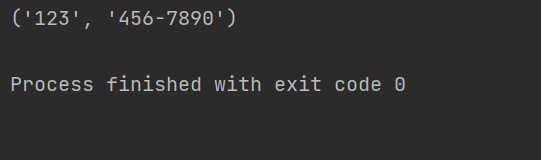
Python正则表达式中group与groups的用法详解
本文主要介绍了Python正则表达式中group与groups的用法详解,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧目录在Python中,正则表达式的group和groups方…...

c++练习题7
1.下列运算符中优先级最高的是 A)> B) C) && D)! 2.以下关于运算符优先级的描述中,正确的是 。 A)!(逻辑非&#x…...

MySQL学习
目录1、数据库定义基本语句(1)数据库操作(2)数据表操作2.数据库操作SQL语句(1)插入数据(2)更新语句(3)删除数据3.数据库查询语句(1)基…...

C语言(强制类型转换)
一.类型转换原则 1.升级:当类型转换出现在表达式时,无论时unsigned还是signed的char和short都会被自动转换成int,如有必要会被转换成unsigned int(如果short与int的大小相同,unsigned short就比int大。这种情况下,uns…...

搭建hadoop高可用集群(二)
搭建hadoop高可用集群(一)配置hadoophadoop-env.shworkerscore-site.xmlhdfs-site.xmlmapred-site.xmlyarn-site.xml/etc/profile拷贝集群首次启动1、先启动zk集群(自动化脚本)2、在hadoop151,hadoop152,hadoop153启动JournalNode…...

CentOS升级内核-- CentOS9 Stream/CentOS8 Stream/CentOS7
官方文档在此 升级原因 当我们安装一些软件(对,我说的就是Kubernetes),可能需要新内核的支持,而CentOS又比较保守,不太升级,所以需要我们手工升级. # 看下目前是什么版本内核 uname -a# 安装公钥 rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.org# 添加仓库,如果…...
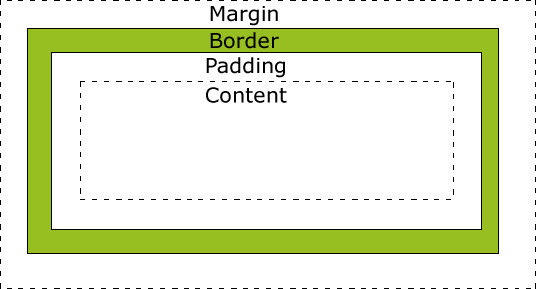
【基础篇】一文掌握css的盒子模型(margin、padding)
1、CSS 盒子模型(Box Model) 所有HTML元素可以看作盒子,在CSS中,"box model"这一术语是用来设计和布局时使用。CSS盒模型本质上是一个盒子,封装周围的HTML元素,它包括:边距,边框,填充,和实际内容。盒模型允许我们在其它元素和周围元素边框之间的空间放置元素…...
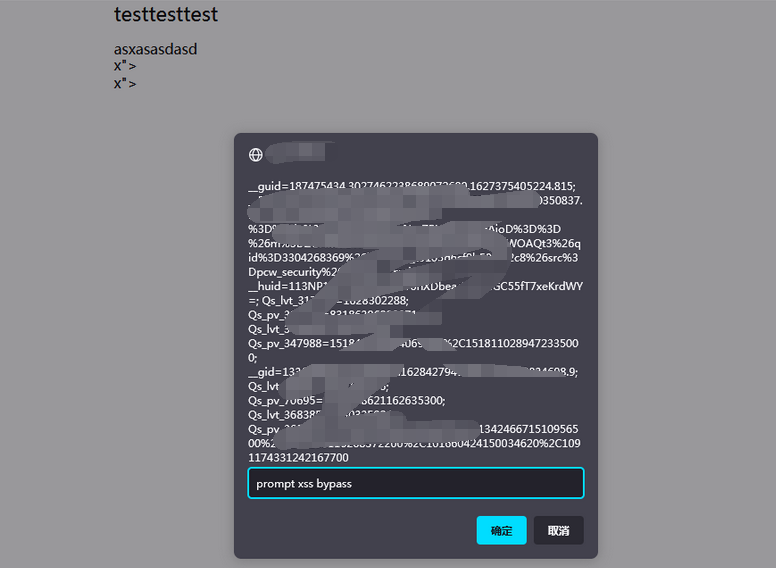
重生之我是赏金猎人-漏洞挖掘(十一)-某SRC储存XSS多次BypassWAF挖掘
0x01:利用编辑器的超链接组件导致存储XSS 鄙人太菜了,没啥高质量的洞呀,随便水一篇文章吧。 在月黑风高的夜晚,某骇客喊我起床挖洞,偷瞄了一下发现平台正好出活动了,想着小牛试刀吧 首先信息收集了一下&a…...

Wails简介
https://wails.io/zh-Hans/docs/introduction 简介 Wails 是一个可让您使用 Go 和 Web 技术编写桌面应用的项目。 将它看作为 Go 的快并且轻量的 Electron 替代品。 您可以使用 Go 的灵活性和强大功能,结合丰富的现代前端,轻松的构建应用程序。 功能…...
)
滑动窗口 AcWing (JAVA)
给定一个大小为 n≤10^6 的数组。 有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。 你只能在窗口中看到 k 个数字。 每次滑动窗口向右移动一个位置。 以下是一个例子: 该数组为 [1 3 -1 -3 5 3 6 7],k 为 33。 窗口位置最小值最大…...
vue小案例
vue小案例 组件化编码流程 1.拆分静态组件,按功能点拆分 2.实现动态组件 3.实现交互 文章目录vue小案例组件化编码流程1.父组件给子组件传值2.通过APP组件给子组件传值。3.案例实现4.项目小细节1.父组件给子组件传值 父组件给子组件传值 1.在父组件中写好要传的值&a…...

阅读笔记3——空洞卷积
空洞卷积 1. 背景 空洞卷积(Dilated Convolution)最初是为解决图像分割的问题而提出的。常见的图像分割算法通常使用池化层来增大感受野,同时也缩小了特征图尺寸,然后再利用上采样还原图像尺寸。特征图先缩小再放大的过程造成了精…...
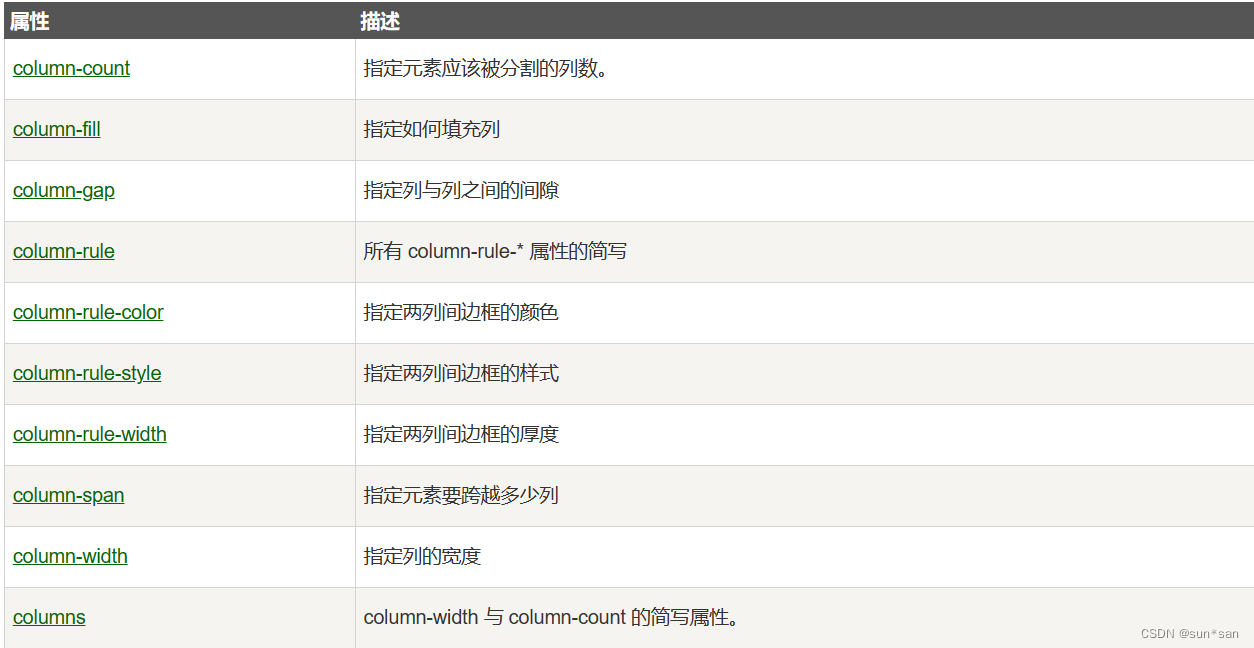
CSS系统学习总结
目录 CSS边框 CSS背景 CSS3渐变 线性渐变(Linear Gradients)- 向下/向上/向左/向右/对角方向 语法 线性渐变(从上到下) 线性渐变(从左到右) 线性渐变(对角) 使用角度 使用多…...

阿里一面:你做过哪些代码优化?来一个人人可以用的极品案例
前言 在尼恩读者50交流群中,尼恩经常指导小伙伴改简历。 改简历所涉及的一个要点是: 在 XXX 项目中,完成了 XXX 模块的代码优化 另外,在面试的过程中,面试官也常常喜欢针对提问,来考察候选人对代码质量的追…...
Android NFC 标签读写Demo与历史漏洞概述
文章目录前言NFC基础1.1 RFID区别1.2 工作模式1.3 日常应用NFC标签2.1 标签应用2.2 应用实践2.3 标签预览2.4 前台调度NFC开发3.1 NDEF数据3.2 标签的调度3.3 读写Demo3.4 Demo演示历史漏洞4.1 中继攻击4.2 预览伪造4.3 篡改卡片4.4 其它漏洞总结前言 NFC 作为 Android 手机一…...

亿级高并发电商项目-- 实战篇 --万达商城项目 六(编写角色管理、用户权限(Spring Security认证授权)、管理员管理等模块)
专栏:高并发---前后端分布式 👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信…...

博视像元获近5000万元融资,主攻半导体前道及锂电高端部件供应
这两年各大车企与电池厂商都在快速新建产能,尤其上游原材料成本大增,反映到产业链上巨头都在寻求增效,高端制造技术投入也大幅增长。比如这家,高端工业相机提供商「博视像元」近期宣布完成近5000万的天使加轮融资,投资…...

SpringCloud-断路器Hystrix
一、降级使用1、添加依赖<!--hystrix--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-hystrix</artifactId></dependency>2、启动类添加注解EnableCircuitBreakerSpringBoot…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
