GAMES101-计算机图形学入门 LEC4: TRANSFORMATION-3D
本节课程视频地址:https://www.bilibili.com/video/BV1X7411F744/?p=4
补充上一节课的一个内容,旋转矩阵的逆矩阵是它的转置,也就是说有R−θ=Rθ−1=RθTR_{-\theta} = R_\theta^{-1}=R_\theta^TR−θ=Rθ−1=RθT
上节课讲了,二维变换中的绕原点的旋转、缩放、切变,以及齐次坐标,还有通过简单变换组合成复杂变换。
这节课先讲三维变换,然后讲困难且重要的观测变换(Viewing Transformation)
文章目录
- 三维变换(3D Transformation)
- 缩放
- 平移
- 旋转
- Rodrigues 旋转公式
- 观测变换 (Viewing transformation)
- 视图变换 (View transformation)
- 投影变换(Perspective Projection)
- 正交投影
- 透视投影
三维变换(3D Transformation)
三维的齐次坐标:
- 点:(x,y,z,1)T(x,y,z,1)^T(x,y,z,1)T
- 向量:(x,y,z,0)T(x,y,z,0)^T(x,y,z,0)T
注:(x,y,z,w)其中w!=0 表示的是点(x/w,y/w,z/w)
齐次坐标使用4维矩阵来表示仿射变换:
[x′y′z′1]=[abctxdeftyghitz0001]⋅[xyz1]\begin{bmatrix} x'\\ y' \\ z' \\ 1 \end{bmatrix}= \begin{bmatrix} a&b&c&t_x\\ d&e&f&t_y\\ g&h&i&t_z \\ 0&0&0&1 \end{bmatrix} \cdot \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} x′y′z′1=adg0beh0cfi0txtytz1⋅xyz1
注:仿射变换中是先线性变换(也就是绕原点所作的变换)再平移变换。
缩放
[x′y′z′1]=[sx0000sy0000sz00001]⋅[xyz1]\begin{bmatrix} x'\\ y' \\ z' \\ 1 \end{bmatrix}= \begin{bmatrix} s_x&0&0&0\\ 0&s_y&0&0\\ 0&0&s_z&0\\ 0&0&0&1 \end{bmatrix} \cdot \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} x′y′z′1=sx0000sy0000sz00001⋅xyz1
平移
[x′y′z′1]=[100tx010ty001tz0001]⋅[xyz1]\begin{bmatrix} x'\\ y' \\ z' \\ 1 \end{bmatrix}= \begin{bmatrix} 1&0&0&t_x\\ 0&1&0&t_y\\ 0&0&1&t_z\\ 0&0&0&1 \end{bmatrix} \cdot \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} x′y′z′1=100001000010txtytz1⋅xyz1
旋转
三维的旋转分为绕x轴旋转、绕y轴旋转和绕z轴旋转。
Rx(α)=[10000cosα−sinα00sinαcosα00001]R_x(\alpha) = \begin{bmatrix} 1&0&0&0\\ 0&cos\alpha&-sin\alpha&0\\ 0&sin\alpha&cos\alpha&0\\ 0&0&0&1 \end{bmatrix}\\ Rx(α)=10000cosαsinα00−sinαcosα00001
Ry(α)=[cosα0sinα00100−sinα0cosα00001]R_y(\alpha) = \begin{bmatrix} cos\alpha&0&sin\alpha&0\\ 0&1&0&0\\ -sin\alpha&0&cos\alpha&0\\ 0&0&0&1 \end{bmatrix} Ry(α)=cosα0−sinα00100sinα0cosα00001
Rz(α)=[cosα−sinα00−sinαcosα0000100001]R_z(\alpha) = \begin{bmatrix} cos\alpha&-sin\alpha&0&0\\ -sin\alpha&cos\alpha&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix} Rz(α)=cosα−sinα00−sinαcosα0000100001
注意旋转矩阵Ry(α)R_y(\alpha)Ry(α)的sinαsin\alphasinα的正负号是和另外两个相反的。其实没有反,因为这是一个右手系的坐标轴,绕x轴逆时针旋转的方向是在y0z平面中y轴旋转到z轴的方向,绕z轴旋转的方向是在x0y平面中x轴旋转到y轴的方向,而绕y轴旋转的方向在z0x平面中是从z轴旋转到x轴的方向。以x0y平面的旋转为例:x′=xcosα−ysinαx' = xcos\alpha - ysin\alphax′=xcosα−ysinα,即要得到x′x'x′需要乘上y轴原始坐标的−sinα-sin\alpha−sinα。所以在z0x平面内,要得到z轴所在坐标:z′=zcosα−xsinαz' = zcos\alpha - xsin\alphaz′=zcosα−xsinα。清晰的记忆方法,以绕x轴旋转为例,绕x轴旋转在y0z平面内是从y轴到z轴的方向,y′=ycosα−zsinαy' = y\cos\alpha - z\sin\alphay′=ycosα−zsinα即转离y轴的方向就减,$z’ = z\cos\alpha + y\sin\alpha $ 即朝z轴转的方向就加。
Rodrigues 旋转公式
绕旋转轴 n⃗\vec{n}n 旋转角度 α\alphaα:
形式一:
R(n⃗,α)=cos(α)I+(1−cos(α))n⃗⋅n⃗T+sinα⋅[0−nznynz0−nx−nynx0]R(\vec{n},\alpha)=cos(\alpha) I + (1-cos(\alpha)) \vec{n}\cdot \vec{n}^T + \sin\alpha\cdot \begin{bmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \\ \end{bmatrix} R(n,α)=cos(α)I+(1−cos(α))n⋅nT+sinα⋅0nz−ny−nz0nxny−nx0
形式二:
R(n⃗,α)=I+sinα⋅[0−nznynz0−nx−nynx0]+(1−cos(α))⋅[0−nznynz0−nx−nynx0]2R(\vec{n},\alpha)= I + \sin\alpha\cdot \begin{bmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \\ \end{bmatrix} + (1-cos(\alpha))\cdot{\begin{bmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \\ \end{bmatrix}}^2 R(n,α)=I+sinα⋅0nz−ny−nz0nxny−nx0+(1−cos(α))⋅0nz−ny−nz0nxny−nx02
证明:
https://www.cnblogs.com/wtyuan/p/12324495.html
观测变换 (Viewing transformation)
视图变换 (View transformation)
什么是视图变换
想象一下拍照:
- 首先要找一个好的背景,把人的位置和人与背景的相对位置安排好(模型变换);
- 然后要找一个好的角度(视图变换);
- 最后按快门(投影变换)。
定义相机:
- 位置向量 Postion: e⃗\vec{e}e
- 朝向 Look-at direction: g⃗\vec{g}g
- 相机向上的方向 Up direction (垂直于朝向) : t⃗\vec{t}t
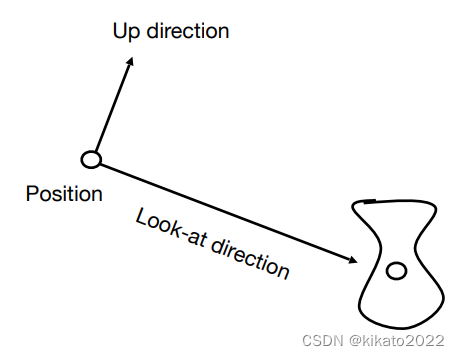
约定:相机永远放在原点,相机永远以+y为向上方向,相机永远朝-z方向看。 也就是进行视图变换时要将所有对象和相机一起做变换,直到相机在原点,朝向-z,以+y为正方向。
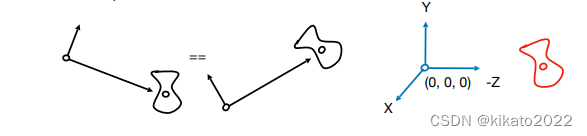
如何将相机从它原来的位置移到约定位置
- 平移 e⃗\vec{e}e到原点;
- 旋转 g⃗\vec{g}g 到 -z 方向;
- 旋转 t⃗\vec{t}t 到 +y 方向
- 旋转 g⃗×t⃗\vec{g} \times \vec{t}g×t 到 +x 方向
如何求出将相机旋转到约定位置的旋转矩阵?
先平移到原点:
Tview=[100−xe010−ye001−ze0001]T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} Tview=100001000010−xe−ye−ze1
再考虑它的逆旋转,找到三个特殊向量的旋转,即 x^\hat{x}x^ 到 g^×t^\hat{g} \times \hat{t}g^×t^, y^\hat{y}y^ 到 t^\hat {t}t^,z^\hat{z}z^ 到 −g^-\hat{g}−g^,就能找到这个逆旋转的旋转矩阵:
Rreview−1=[xg^×t^xt^x−g^0yg^×t^yt^y−g^0zg^×t^zt^z−g^00001]R_{review}^{-1} = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_{\hat{t}} & x_{-\hat{g}} & 0\\ y_{\hat{g}\times\hat{t}} & y_{\hat{t}} & y_{-\hat{g}} & 0\\ z_{\hat{g}\times\hat{t}} & z_{\hat{t}} & z_{-\hat{g}} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} Rreview−1=xg^×t^yg^×t^zg^×t^0xt^yt^zt^0x−g^y−g^z−g^00001
旋转矩阵是正交矩阵,上面这个矩阵显然符合,旋转矩阵的逆矩阵就是它的转置:
Rreview=[xg^×t^yg^×t^zg^×t^0xt^yt^zt^0x−g^y−g^z−g^00001]R_{review} = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rreview=xg^×t^xt^x−g^0yg^×t^yt^y−g^0zg^×t^zt^z−g^00001
总结:将所有对象和相机一起做变换,直到相机在原点,朝向-z,以+y为正方向。
这就是视图变换。
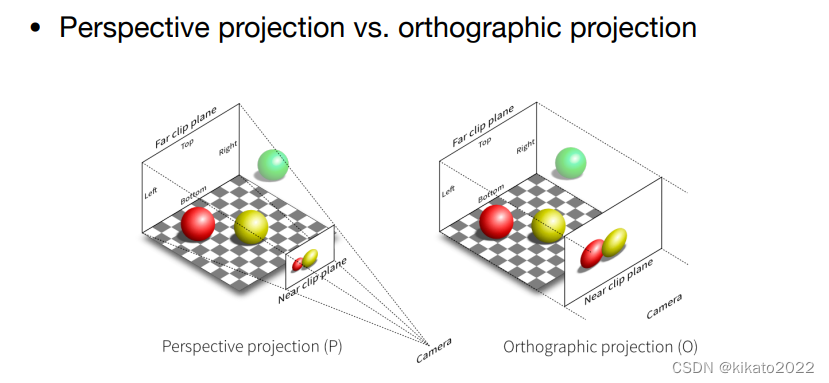
投影变换(Perspective Projection)
正交投影(Orthographic projection)
透视投影(Perspective projection)
区别:正交投影没有近大远小而透视投影有。
正交投影
做法一:
假设已经进行了视图变换(即相机在原点,朝向-z,以+y为向上方向)
第一步,把所有点的z坐标变为0;
第二步,将得到的二维平面坐标做平移和缩放,让它们装在[−1,−1]2[-1,-1]^2[−1,−1]2 这个正方形里。(至于为什么要进行这一步操作,这是一个约定俗成的办法,可以方便之后的操作)
做法二:(正规做法)
实际的计算机图形学操作中,还有一个比简单地把z扔掉更方便的做法:
同样,假设已经进行了视图变换(即相机在原点,朝向-z,以+y为向上方向)
假设此时所有物体装在一个 [l,r]×[b,t]×[f,n][l, r]\times[b,t] \times [f, n][l,r]×[b,t]×[f,n] 的长方体内,将这个长方体映射到 [−1,1]3[-1, 1]^3[−1,1]3 的正方体:
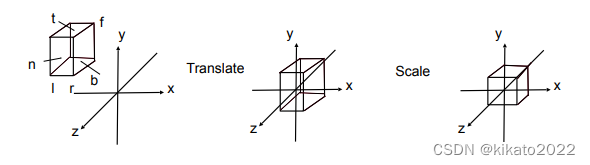
先平移,再缩放:
Mortho=[2r−l00002t−b00002n−f00001][100−r+l2010−t+b2001−n+f20001]M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0& 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix} Mortho=r−l20000t−b20000n−f200001100001000010−2r+l−2t+b−2n+f1
透视投影
回顾齐次坐标的一个重要性质:
(x,y,z,1)(x,y,z,1)(x,y,z,1)表示一个点,
(kx,ky,kz,k!=0)(kx,ky,kz,k!=0)(kx,ky,kz,k!=0)也表示该点,
(xz,yz,z2,z!=0)(xz,yz,z^2,z!=0)(xz,yz,z2,z!=0)也表示该点。
做法:
将一个截头锥体,“挤压”到一个长方体:
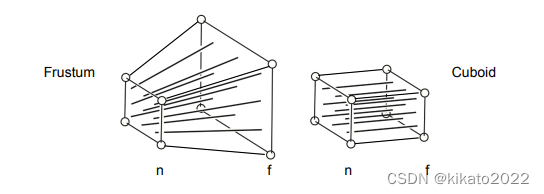
如何“挤压”呢?
提前告诉你,这个“挤压”可以用一个矩阵表示,一般叫投影变换矩阵,那么这个矩阵怎么求呢?
观察,该“挤压”的特点:
x坐标和 y坐标很明显有相似关系
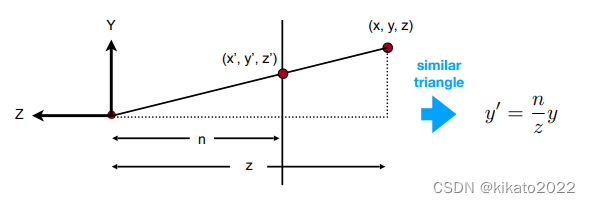
y′=nzy,x′=nzxy' = \frac{n}{z}y,\ \ \ x' = \frac{n}{z}xy′=zny, x′=znx
z坐标怎么变目前还不知道,用齐次坐标表示:
[xyz1]→[nx/zny/zunknown1]==[nxnyunknownz]\begin{bmatrix} x\\y\\z\\1 \end{bmatrix}\rightarrow \begin{bmatrix} nx/z\\ny/z\\unknown\\1 \end{bmatrix} == \begin{bmatrix} nx\\ny\\unknown\\z \end{bmatrix} xyz1→nx/zny/zunknown1==nxnyunknownz
这样已经可以得到这个变换矩阵的一大部分了:
Mpersp→ortho=[n0000n00????00n0]M_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & n & 0 \end{bmatrix} Mpersp→ortho=n0?00n?000?n00?0
那么该矩阵的第三行怎么求?
利用两点:
-
近平面上的点不会发生改变
[xyn1]→[xyn1]==[nxnyn2n]\begin{bmatrix} x\\y\\n\\1 \end{bmatrix} \rightarrow \begin{bmatrix} x\\y\\n\\1 \end{bmatrix} == \begin{bmatrix} nx\\ ny\\ n^2\\ n \end{bmatrix} xyn1→xyn1==nxnyn2n
因为n2n^2n2与xxx无关,所以第三行的第一个和第二个元素是0,也就是说对于透视投影矩阵的第三行有:
[00AB][xyn1]=n2\begin{bmatrix} 0&0&A&B \end{bmatrix} \begin{bmatrix} x\\y\\n\\1 \end{bmatrix}=n^2 [00AB]xyn1=n2 -
远平面上与z轴相交的点不会改变
[00f1]→[00f1]==[00f2f]\begin{bmatrix} 0\\0\\f\\1 \end{bmatrix}\rightarrow \begin{bmatrix} 0\\0\\f\\1 \end{bmatrix}== \begin{bmatrix} 0\\0\\f^2\\f \end{bmatrix} 00f1→00f1==00f2f
也就是:
[00AB][00f2f]=f2\begin{bmatrix} 0 & 0 & A & B \end{bmatrix} \begin{bmatrix} 0\\0\\f^2\\f \end{bmatrix} = f^2 [00AB]00f2f=f2
可以建立方程组求解A和B了:
An+B=n2Af+B=f2An+B=n^2\\ Af+B=f^2 An+B=n2Af+B=f2
解得
A=n+f,B=−nfA = n+f,\ \ \ B= -nf A=n+f, B=−nf
得到该矩阵为:
Mpersp→ortho=[n0000n0000n+f−nf00n0]M_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & n & 0 \end{bmatrix} Mpersp→ortho=n0000n0000n+fn00−nf0
最后
Mpersp=MorthoMpersp→orthoM_{persp} = M_{ortho}M_{persp\rightarrow ortho} Mpersp=MorthoMpersp→ortho
问题:对于截头锥体中间的点,它的z坐标怎么变?
[n0000n0000n+f−nf00n0][xyz1]=[nxnynz+fz−nfz]\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & n & 0 \end{bmatrix} \begin{bmatrix} x\\y\\z\\1 \end{bmatrix}= \begin{bmatrix} nx\\ny\\nz+fz-nf\\z \end{bmatrix} n0000n0000n+fn00−nf0xyz1=nxnynz+fz−nfz
记
f(z)=nz+fz−nfz−z=1z[−z2+(n+f)z−nf]f(z) = \frac{nz+fz-nf}{z}-z = \frac{1}{z}[-z^2+(n+f)z -nf] f(z)=znz+fz−nf−z=z1[−z2+(n+f)z−nf]
对于中括号中的二次函数,开口向下,且两个零点为z=f和z=n,所以中括号中的二次函数在f<n<z这个区间里大于0,又z<0,所以f(z)小于0,即z的坐标会变小(朝远平面方向变)。
相关文章:

GAMES101-计算机图形学入门 LEC4: TRANSFORMATION-3D
本节课程视频地址:https://www.bilibili.com/video/BV1X7411F744/?p4 补充上一节课的一个内容,旋转矩阵的逆矩阵是它的转置,也就是说有R−θRθ−1RθTR_{-\theta} R_\theta^{-1}R_\theta^TR−θRθ−1RθT 上节课讲了,…...

robot实战:截取字符串
一:变量标识符号(1) Scalar型变量: "$"作为标识符号,例如:${var}, 这个打印log时只能用logset赋值:a: ${var} Set Variable abcb:${var2} Set Variable If ${Var}abc efgh ace 如果var的值和abc相等…...

【面经】滴滴测开一面
滴滴测开一面 面试官自我介绍面试者自我介绍大概实习多久?你在在校经历比较丰富,说一下打ACM那些比赛中的一些经验,找一些具体的项目说一下在打ACM中团队里几个人? 你负责什么?在上段实习的过程中都做了哪些事情&…...

数据治理-主数据
二、某企业集团旗下有房地产、供应链、物流、酒店等多个业务子公司,为了统一管理,集团推进数字化转型,建立了统一的数据仓库,各子公司将数据集成到集团信息部负责管理的 数据平台。集团在实施数据治理过程中,发现各业务…...

软考-中级-软件设计师-成绩
低分飘过,备考经验主要就是刷题。...

学习笔记<二> MySQL学习(3):分库、分表
文章目录为什么分库分表一、垂直分片、水平分片二、常用的数据分片策略三、垂直分表、垂直分库、水平分库、水平分表四、垂直切分、水平切分优缺点五、数据分片规则六、分库分表带来的问题本文参考博主「小Y是我的」的文章,原文链接:https://blog.csdn.n…...
重生之我是赏金猎人-SRC漏洞挖掘(八)-记一次移花接木的GetShell
0x00:前言 https://github.com/J0o1ey/BountyHunterInChina 欢迎亲们点个star 作者:RGM78sec 某天测厂商业务时,发现其中有一个提供音乐播放业务的资产,正好里面有我想听的歌,于是就有了这篇文章 0x01:…...
:数仓搭建)
离线数仓(五):数仓搭建
文章目录一、创建数据库二、ODS 层(原始数据层)三、DWD 层(明细数据层)3.1 get_json_object 函数使用3.2 启动日志表 DWD层创建四、DWS 层(服务数据层)五、DWT 层(数据主题层)六、AD…...
安装SQL Server2017 过程中报KB29119355失败的解决方案
SQLServer 2017脱机版下载地址:http://download.microsoft.com/download/6/4/A/64A05A0F-AB28-4583-BD7F-139D0495E473/SQLServer2017-x64-CHS-Dev.isoMicrosoft SQL Server Management Studio 18管理工具下载https://learn.microsoft.com/zh-cn/sql/ssms/download-…...
2023年浙江建筑特种工(施工升降机)真题题库及答案
百分百题库提供特种工(施工升降机)考试试题、特种工(施工升降机)考试预测题、特种工(施工升降机)考试真题、特种工(施工升降机)证考试题库等,提供在线做题刷题,在线模拟考…...

2023年进入互联网行业好找工作吗?
俗话说:选择大于努力。年后求职小高峰,大家在找工作的时候选择肯定也多了。说真,不是人人都有铁饭,普通家庭的孩子想要在2023年进入互联网行业去找工作可能吗?01有一点大家要清楚,2022年是进入过一个寒冬的…...

基于策略模式企业实战中策略命中设计
背景 在公司实际项目项目开发中,有一个策略命中的开发需求。根据用户请求参数的不同来动态返回不同的业务数据。比如说有城市、客户年龄、请求时间3个策略维度,不同的城市返回不同的地区的地标,根据时间地标的背景色要发生变化等等的需求。当…...

pod生命周期,pod控制器service
一:pod-demo.yml apiVersion: v1 # <string> kind: Pod # <string> metadata: # <Object>对象:键值对的集合,又称为映射(mapping)/ 哈希(hashes) / 字…...

SAP FICO 深入讲解会计凭证
SAP系统在数据处理,无论是业务处理,还是财务处理都会产生大量的凭证,无论是什么凭证,最终的反映形式就是 会计凭证。 1.凭证原则Code 每笔记账都一直以凭证形式存储,每一凭证都作为前后一致的单位保留在系统中…...

LeetCode 2341. 数组能形成多少数对
【LetMeFly】2341.数组能形成多少数对 力扣题目链接:https://leetcode.cn/problems/maximum-number-of-pairs-in-array/ 给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤: 从 nums 选出 两个 相等的 整数从 nums…...

PHPStorm常用快捷键
alt 1 左侧项目结构树隐藏或者显示,这两个组合键的使用可以切换“项目结构树”和当前打开文件之间的焦点。 alt 2 隐藏或者显示 Favorites Ctrl Shift F12 切换到最大编辑器窗口,隐藏其他所有的工具窗口。例如项目结构树、Favorites、Terminal等。…...
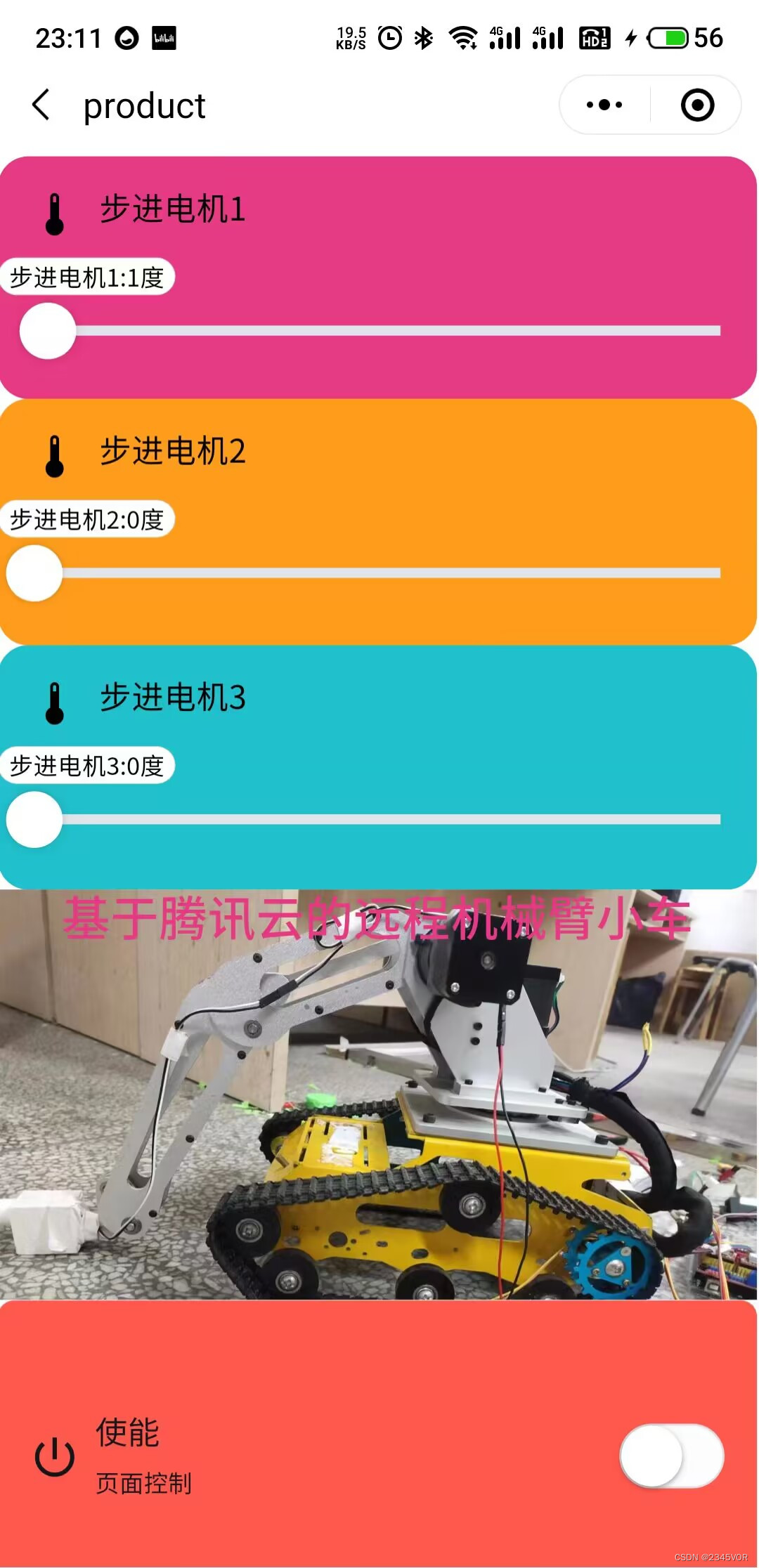
【基于腾讯云的远程机械臂小车】
【基于腾讯云的远程机械臂小车】1. 项目来源1.1 项目概述1.2 系统结构1.3 设计原理2. 硬件搭建2.1 CH32V307开发板2.2 Arduino mega25602.3 富斯I6遥控器2.4 机械臂小车2.5 ESP8266 MCU2.5.1 ESP8266 MCU介绍2.5.2 腾讯云固件烧录3. 软件设计3.1 两种控制方式3.1.1 富斯I6遥控机…...

兼职任务平台收集(一)分享给有需要的朋友们
互联网时代,给人们带来了很大的便利。信息交流、生活缴费、足不出户购物、便捷出行、线上医疗、线上教育等等很多。可以说,网络的时代会一直存在着。很多人也在互联网上赚到了第一桶金,这跟他们的努力和付出是息息相关的。所谓一份耕耘&#…...

MarkDown中公式的编辑
MarkDown中公式的编辑生成目录积分插入编号常见希腊字母大小写分式括号求和积分连乘根式三角函数运算符集合运算箭头逻辑运算符约等于向量绝对值申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计1077字&…...
解决jupyter以及windows系统中pycharm编译器画图的中文乱码问题大全
一、jupyter环境下中文乱码问题解决 我们在jupyter的notebook中使用matplotlib画图的时候,经常性的会遇见一些中文乱码显示□的情况,如下所示: 在此,网上给出的方法大多是以下的解决方法: import matplotlib.pyplot as pltplt.rcParams[fo…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
