2023年进入互联网行业好找工作吗?
俗话说:选择大于努力。年后求职小高峰,大家在找工作的时候选择肯定也多了。
说真,不是人人都有铁饭,普通家庭的孩子想要在2023年进入互联网行业去找工作可能吗?

01
有一点大家要清楚,2022年是进入过一个寒冬的一个情况,但是2023年的话寒冬到了一定极致,那肯定又是一个新的彩虹就会出来。
伴随数字化社会的发展,人才缺口也在拉大,IT互联网企业对人才的需求,每年以约20%的速度在增长,据国内权威统计,我国信息化人才总需求量高达1500万至2000万人。
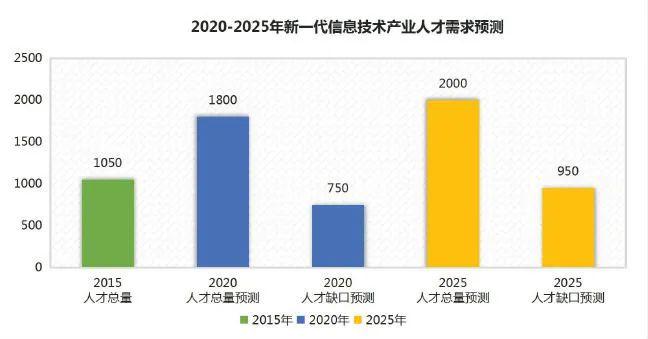
在就业环境相对严峻,而IT技术进步发展又势不可挡的双重因素下,掌握一门能在行业中发展的技能,用过硬的技术跟行业对话,是职业人立足职场的必要装备。
其次,对于普普通通的你我,不拼爹、不攀关系、想通过读书靠双手拼一个出人头地的普通人来说,程序员依然可以作为首要选择。
一份可以让自己快速积累财富,在大城市扎根,成家立业,毕业就能月薪上万的工作,想想也只能是程序员相关岗位了。
02
不过比起互联网高速发展的那几年,现在进入IT圈的新人,的确要学更多的知识,背更多的八股文,掌握更多的技术。
因为“卷”嘛~但现实问题避无可避,哪里都卷。
当你专注学习时候,会感觉自己的每一个细胞都在进化,而正是这样的力量,会让你的职业生涯越走越宽广。

IT互联网高速飞奔的时代,技术实时更新,新来旧走,就连曾一度为霸者的FLASH技术,如今早已被遗弃淘汰。
在移动互联网爆发的时代,多少传统公司还未来得及转型就被拍死,就足以可预见,学习力对互联网对技术人的重要性。
在互联网大环境如此动荡的当下,学习力也是职场人对抗不确定性的重要法宝。
不论哪家公司都期望吸纳能都不断学习进步的员工,现在不少公司一边裁员一边招人,也是在吸收别家释放出的“养料”。

如果你觉得自己对编程还挺稀罕,有那么一些吃苦耐劳的本事,想为自己谋一个前程,做程序员真的不错。
IT行业的入门门槛其实是非常低的,不像是其他行业,不仅需要个人的专业水平到位,还需要各种关系,如果没有相关的人力关系,想要在这个行业得到成长,比较难。而相较于IT行业就不一样了,只要你的技术能力达标,任何事情都可以迎刃而解。
选择培训,是通往IT行业,实现高薪最快的一条路。
相关文章:

2023年进入互联网行业好找工作吗?
俗话说:选择大于努力。年后求职小高峰,大家在找工作的时候选择肯定也多了。说真,不是人人都有铁饭,普通家庭的孩子想要在2023年进入互联网行业去找工作可能吗?01有一点大家要清楚,2022年是进入过一个寒冬的…...

基于策略模式企业实战中策略命中设计
背景 在公司实际项目项目开发中,有一个策略命中的开发需求。根据用户请求参数的不同来动态返回不同的业务数据。比如说有城市、客户年龄、请求时间3个策略维度,不同的城市返回不同的地区的地标,根据时间地标的背景色要发生变化等等的需求。当…...

pod生命周期,pod控制器service
一:pod-demo.yml apiVersion: v1 # <string> kind: Pod # <string> metadata: # <Object>对象:键值对的集合,又称为映射(mapping)/ 哈希(hashes) / 字…...

SAP FICO 深入讲解会计凭证
SAP系统在数据处理,无论是业务处理,还是财务处理都会产生大量的凭证,无论是什么凭证,最终的反映形式就是 会计凭证。 1.凭证原则Code 每笔记账都一直以凭证形式存储,每一凭证都作为前后一致的单位保留在系统中…...

LeetCode 2341. 数组能形成多少数对
【LetMeFly】2341.数组能形成多少数对 力扣题目链接:https://leetcode.cn/problems/maximum-number-of-pairs-in-array/ 给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤: 从 nums 选出 两个 相等的 整数从 nums…...

PHPStorm常用快捷键
alt 1 左侧项目结构树隐藏或者显示,这两个组合键的使用可以切换“项目结构树”和当前打开文件之间的焦点。 alt 2 隐藏或者显示 Favorites Ctrl Shift F12 切换到最大编辑器窗口,隐藏其他所有的工具窗口。例如项目结构树、Favorites、Terminal等。…...
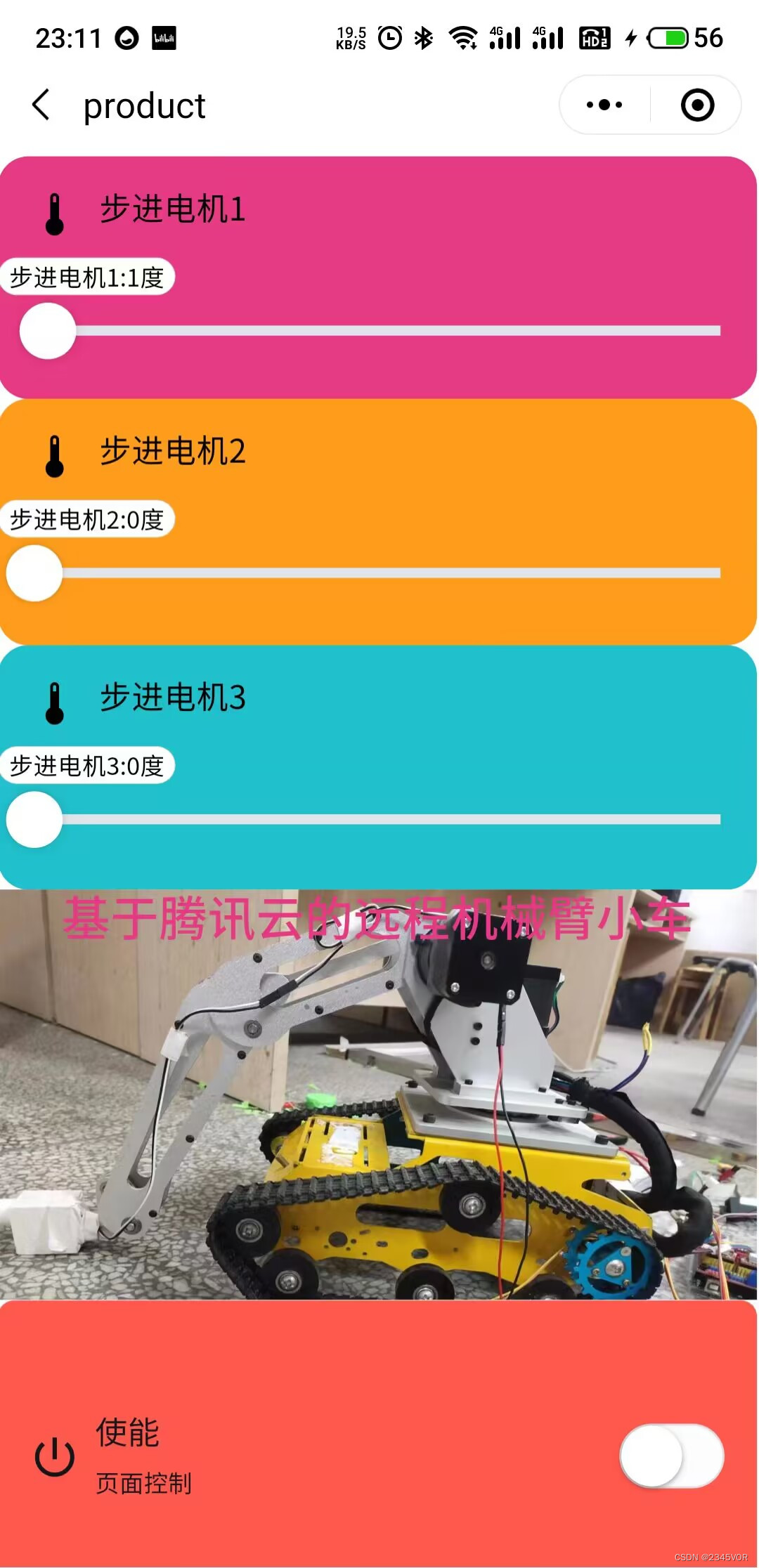
【基于腾讯云的远程机械臂小车】
【基于腾讯云的远程机械臂小车】1. 项目来源1.1 项目概述1.2 系统结构1.3 设计原理2. 硬件搭建2.1 CH32V307开发板2.2 Arduino mega25602.3 富斯I6遥控器2.4 机械臂小车2.5 ESP8266 MCU2.5.1 ESP8266 MCU介绍2.5.2 腾讯云固件烧录3. 软件设计3.1 两种控制方式3.1.1 富斯I6遥控机…...

兼职任务平台收集(一)分享给有需要的朋友们
互联网时代,给人们带来了很大的便利。信息交流、生活缴费、足不出户购物、便捷出行、线上医疗、线上教育等等很多。可以说,网络的时代会一直存在着。很多人也在互联网上赚到了第一桶金,这跟他们的努力和付出是息息相关的。所谓一份耕耘&#…...

MarkDown中公式的编辑
MarkDown中公式的编辑生成目录积分插入编号常见希腊字母大小写分式括号求和积分连乘根式三角函数运算符集合运算箭头逻辑运算符约等于向量绝对值申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计1077字&…...
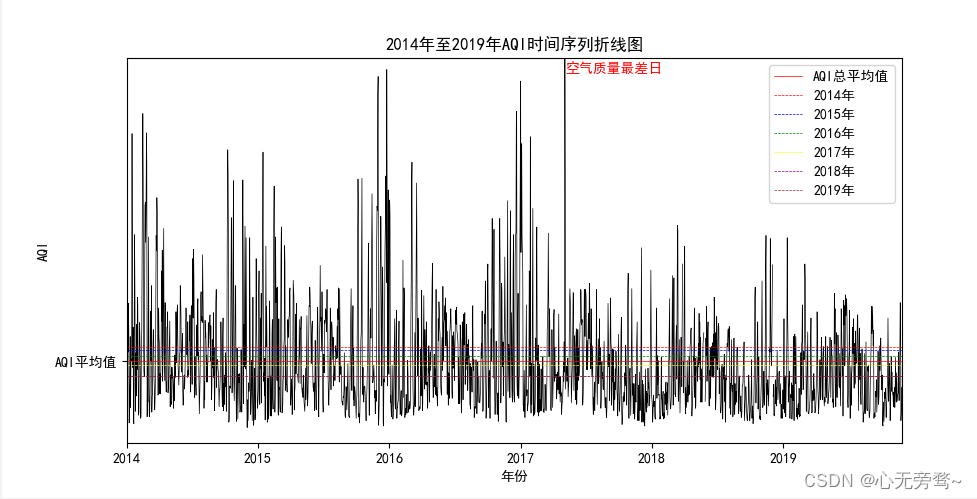
解决jupyter以及windows系统中pycharm编译器画图的中文乱码问题大全
一、jupyter环境下中文乱码问题解决 我们在jupyter的notebook中使用matplotlib画图的时候,经常性的会遇见一些中文乱码显示□的情况,如下所示: 在此,网上给出的方法大多是以下的解决方法: import matplotlib.pyplot as pltplt.rcParams[fo…...
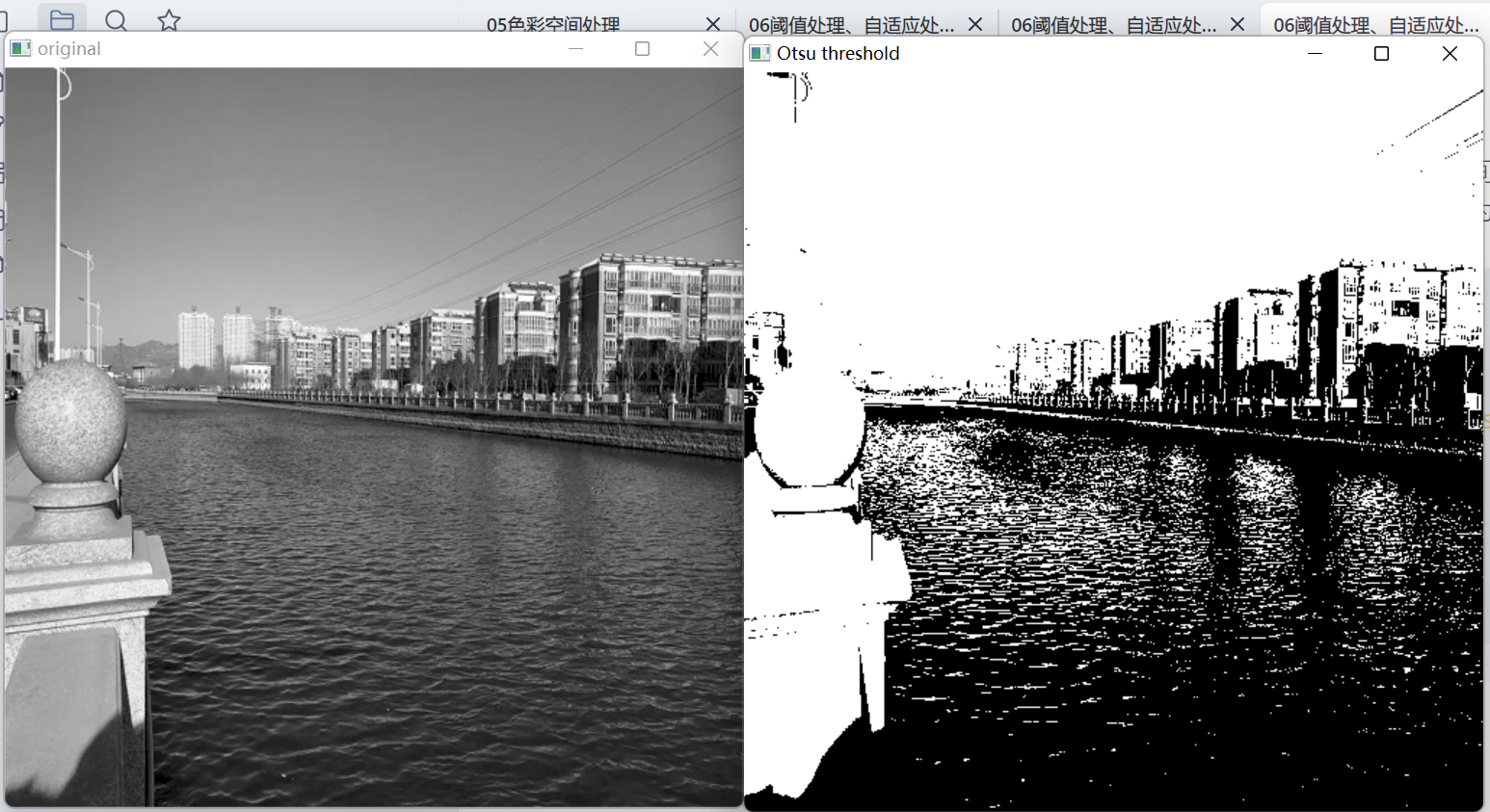
06 OpenCV 阈值处理、自适应处理与ostu方法
1 基本概念 CV2中使用阈值的作用是将灰度图像二值化,即将灰度图像的像素值根据一个设定的阈值分成黑白两部分。阈值处理可以用于图像分割、去除噪声、增强图像对比度等多个领域。例如,在物体检测和跟踪中,可以通过对图像进行阈值处理来提取目…...

RFC7519规范-JWT - json web token
简介 什么是JWT(JSON Web Token) 在介绍JWT之前,我们先来回顾一下利用token进行用户身份验证的流程: 客户端使用用户名和密码请求登录服务端收到请求,验证用户名和密码验证成功后,服务端会签发一个token,再把这个to…...

移动机器人设计与实践课程大纲
MiR移动机器人参考资料:图一 西北工业大学-课程平台图二 清华大学出版社-移动机器人目前,基本都是双一流大学开设此类课程,并且都是至少3-4学分,16学时/学分,48-64学时。(⊙﹏⊙),难办了。咱这只有…...
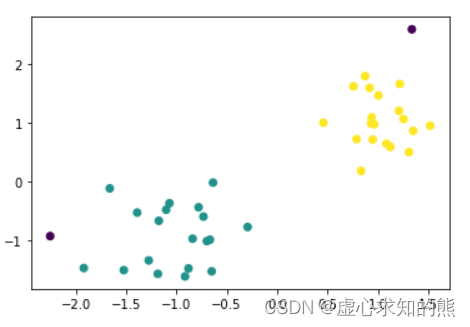
Lesson 7.2 Mini Batch K-Means与DBSCAN密度聚类
文章目录一、Mini Batch K-Means 算法原理与实现二、DBSCAN 密度聚类基本原理与实践1. K-Means 聚类算法的算法特性2. DBSCAN 密度聚类基本原理3. DBSCAN 密度聚类的 sklearn 实现除了 K-Means 快速聚类意外,还有两种常用的聚类算法。(1) 是能…...

11.Dockerfile最佳实践
Dockerfile 最佳实践 Docker官方关于Dockerfile最佳实践原文链接地址:https://docs.docker.com/develop/develop-images/dockerfile_best-practices/ Docker 可以通过从 Dockerfile 包含所有命令的文本文件中读取指令自动构建镜像,以便构建给定镜像。 …...
【企业云端全栈开发实践-1】项目介绍及环境准备、Spring Boot快速上手
本节目录一、 项目内容介绍二、Maven介绍2.1 Maven作用2.2 Maven依赖2.3 本地仓库配置三、Spring Boot快速上手3.1 Spring Boot特点3.2 遇到的Bug:spring-boot-maven-plugin3.3 遇到的Bug2:找不到Getmapping四、开发环境热部署一、 项目内容介绍 本课程…...
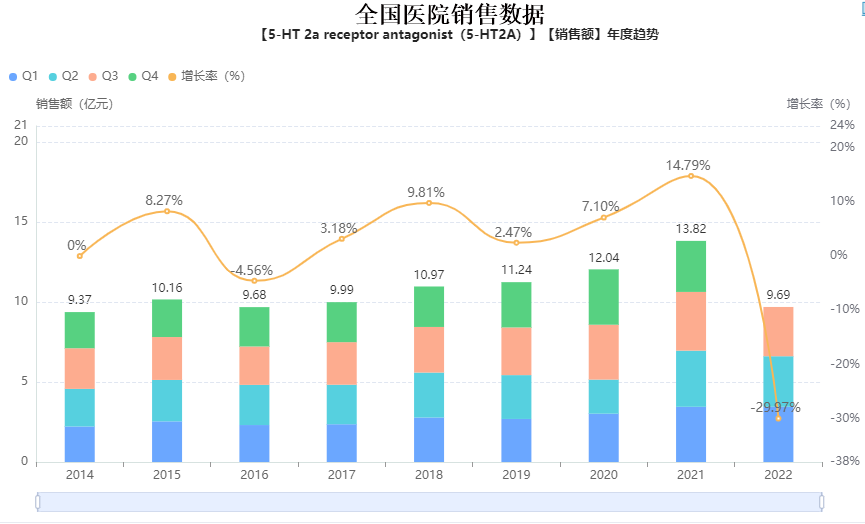
5-HT2A靶向药物|适应症|市场销售-上市药品前景分析
据世界卫生组织称,抑郁症是一种多因素疾病,影响全球约3.5 亿人。中枢神经系统最广泛的单胺 - 血清素 (5-HT) 被认为在这种情况的病理机制中起着至关重要的作用,并且神经递质的重要性被“血清素假说”提升,将抑郁症的存在联系起来 …...

HTTPS协议原理---详解
目录 一、HTTPS 1.加密与解密 2.我们为什么要加密? 3.常见加密方式 ①对称加密 ②非对称加密 4.数据摘要 5.数字签名 二、HTTPS的加密方案 1.只是用对称加密 2.只使用非对称加密 3.双方都使用非对称加密 4.非对称加密+对称加密 中间人攻…...
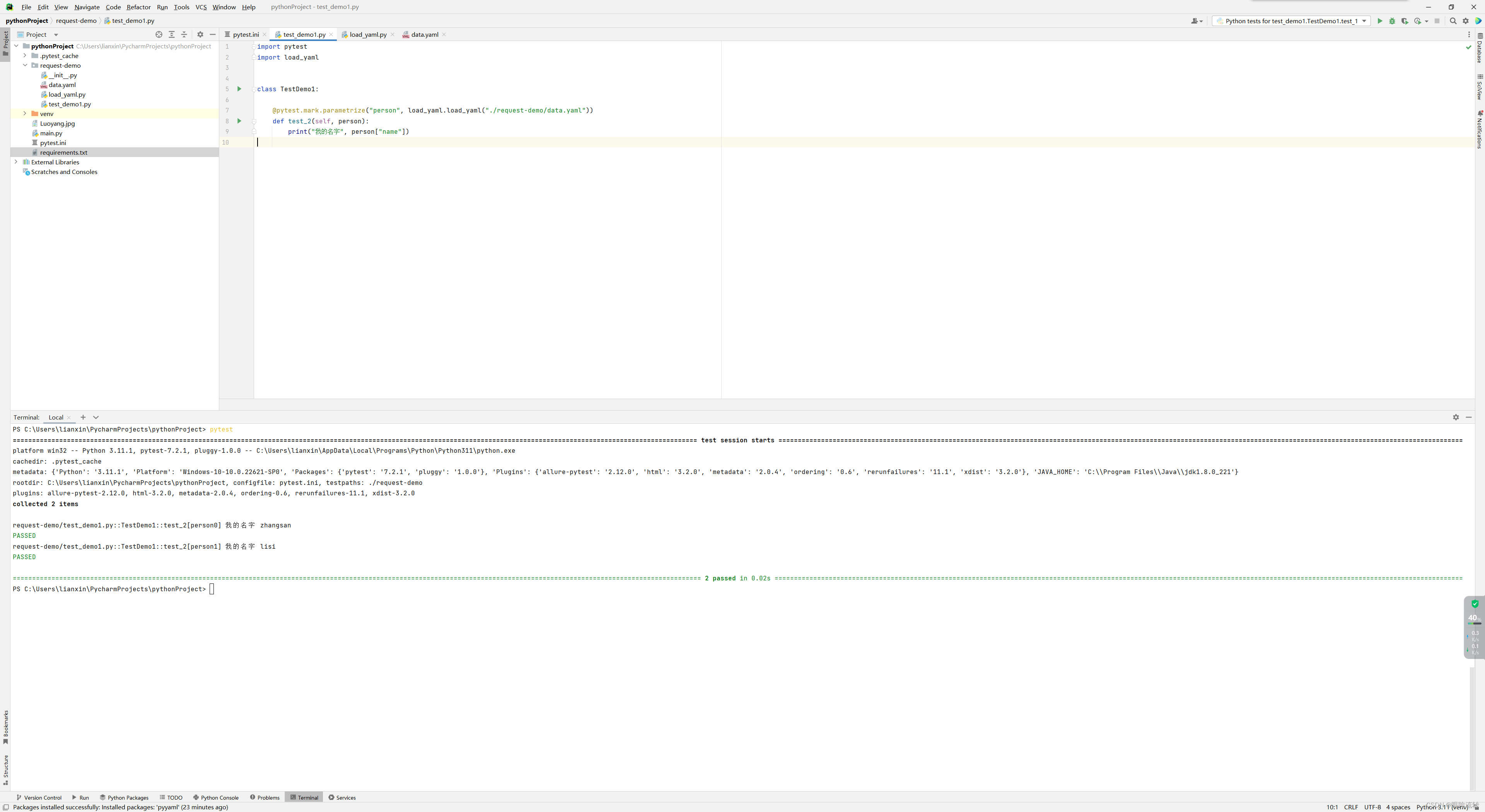
Pytest学习笔记
Pytest学习笔记 1、介绍 1.1、单元测试 单元测试是指在软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试 1.2、单元测试框架 测试发现:从多个py文件里面去找到我们测试用例测试执行:按…...
Fuzz概述
文章目录AFL一些概念插桩与覆盖率边和块覆盖率afl自实现劫持汇编器clang内置覆盖率反馈与引导变异遗传算法fork server机制AFL调试准备AFL一些概念 插桩与覆盖率 边和块 首先,要明白边和块的定义 正方形的就是块,箭头表示边,边表示程序执行…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
