MarkDown中公式的编辑
MarkDown中公式的编辑
- 生成目录
- 积分
- 插入编号
- 常见希腊字母大小写
- 分式
- 括号
- 求和
- 积分
- 连乘
- 根式
- 三角函数
- 运算符
- 集合运算
- 箭头
- 逻辑运算符
- 约等于
- 向量
- 绝对值
申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计1077字,阅读大概需要1分钟
更多学习内容, 欢迎关注我的个人公众号:不懂开发的程序猿
生成目录
在文档开头第一行单独输入 [TOC]
积分
\Gamma(z)=\int_0\infty t^{z-1}e^{-t}dt\,
Γ(z)=∫0∞tz−1e−tdt.\Gamma(z)=\int_0\infty t^{z-1}e^{-t}dt\,. Γ(z)=∫0∞tz−1e−tdt.
插入编号
y=x^2\tag{1}
y=x2(1)y=x^2\tag{1} y=x2(1)
常见希腊字母大小写
\Alpha \alpha \beta \Beta \Gamma \gamma \Delta \delta \Eta \eta \Theta \theta \Lambda \lambda \Pi \pi \Sigma \sigma \Omega \omega \Psi \psi \Phi \phi
AαβBΓγΔδHηΘθΛλΠπΣσΩωΨψΦϕ\Alpha \alpha \beta \Beta \Gamma \gamma \Delta \delta \Eta \eta \Theta \theta \Lambda \lambda \Pi \pi \Sigma \sigma \Omega \omega \Psi \psi \Phi \phi AαβBΓγΔδHηΘθΛλΠπΣσΩωΨψΦϕ
分式
\frac{a+b+c}{d+e+f}
a+b+cd+e+f\frac{a+b+c}{d+e+f} d+e+fa+b+c
括号
\{x\} \langle x \rangle \lceil x \rceil \lfloor x \rfloor
{x}⟨x⟩⌈x⌉⌊x⌋\{x\} \langle x \rangle \lceil x \rceil \lfloor x \rfloor {x}⟨x⟩⌈x⌉⌊x⌋
求和
\sum^{x=n}_{x=1}
∑x=1x=n\sum^{x=n}_{x=1} x=1∑x=n
积分
\int_{x=1}^{x=5}
\iint_{x=1}^{x=2}
\iiint_{x=1}^{x=3}
∫x=1x=5∬x=1x=2∭x=1x=3\int_{x=1}^{x=5} \iint_{x=1}^{x=2} \iiint_{x=1}^{x=3} ∫x=1x=5∬x=1x=2∭x=1x=3
连乘
\prod_{i=1}^{i=n}
∏i=1i=n\prod_{i=1}^{i=n} i=1∏i=n
根式
\sqrt{a+b}
\sqrt[3] {\frac xy}
a+bxy3\sqrt{a+b} \sqrt[3] {\frac xy} a+b3yx
三角函数
\arctan x \sin x
arctanxsinx\arctan x \sin x arctanxsinx
运算符
\lt \gt \le \ge \ne
<>≤≥≠\lt \gt \le \ge \ne <>≤≥=
集合运算
\cup \cap \subset \subseteq \subsetneq \supset \in \emptyset \varnothing
∪∩⊂⊆⊊⊃∈∅∅\cup \cap \subset \subseteq \subsetneq \supset \in \emptyset \varnothing ∪∩⊂⊆⊊⊃∈∅∅
\to \rightarrow \leftarrow \Rightarrow \Leftarrow
箭头
→→←⇒⇐\to \rightarrow \leftarrow \Rightarrow \Leftarrow →→←⇒⇐
逻辑运算符
\land \forall \exist \top \bot \vdash \vDash
∧∀∃⊤⊥⊢⊨\land \forall \exist \top \bot \vdash \vDash ∧∀∃⊤⊥⊢⊨
约等于
\approx
≈\approx ≈
向量
\hat \theta \overline x \vec x \overrightarrow {xyz} \dot x
θ^x‾x⃗xyz→x˙\hat \theta \overline x \vec x \overrightarrow {xyz} \dot x θ^xxxyzx˙
绝对值
\vert x \vert
∣x∣\vert x \vert ∣x∣
–end–
相关文章:

MarkDown中公式的编辑
MarkDown中公式的编辑生成目录积分插入编号常见希腊字母大小写分式括号求和积分连乘根式三角函数运算符集合运算箭头逻辑运算符约等于向量绝对值申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计1077字&…...
解决jupyter以及windows系统中pycharm编译器画图的中文乱码问题大全
一、jupyter环境下中文乱码问题解决 我们在jupyter的notebook中使用matplotlib画图的时候,经常性的会遇见一些中文乱码显示□的情况,如下所示: 在此,网上给出的方法大多是以下的解决方法: import matplotlib.pyplot as pltplt.rcParams[fo…...
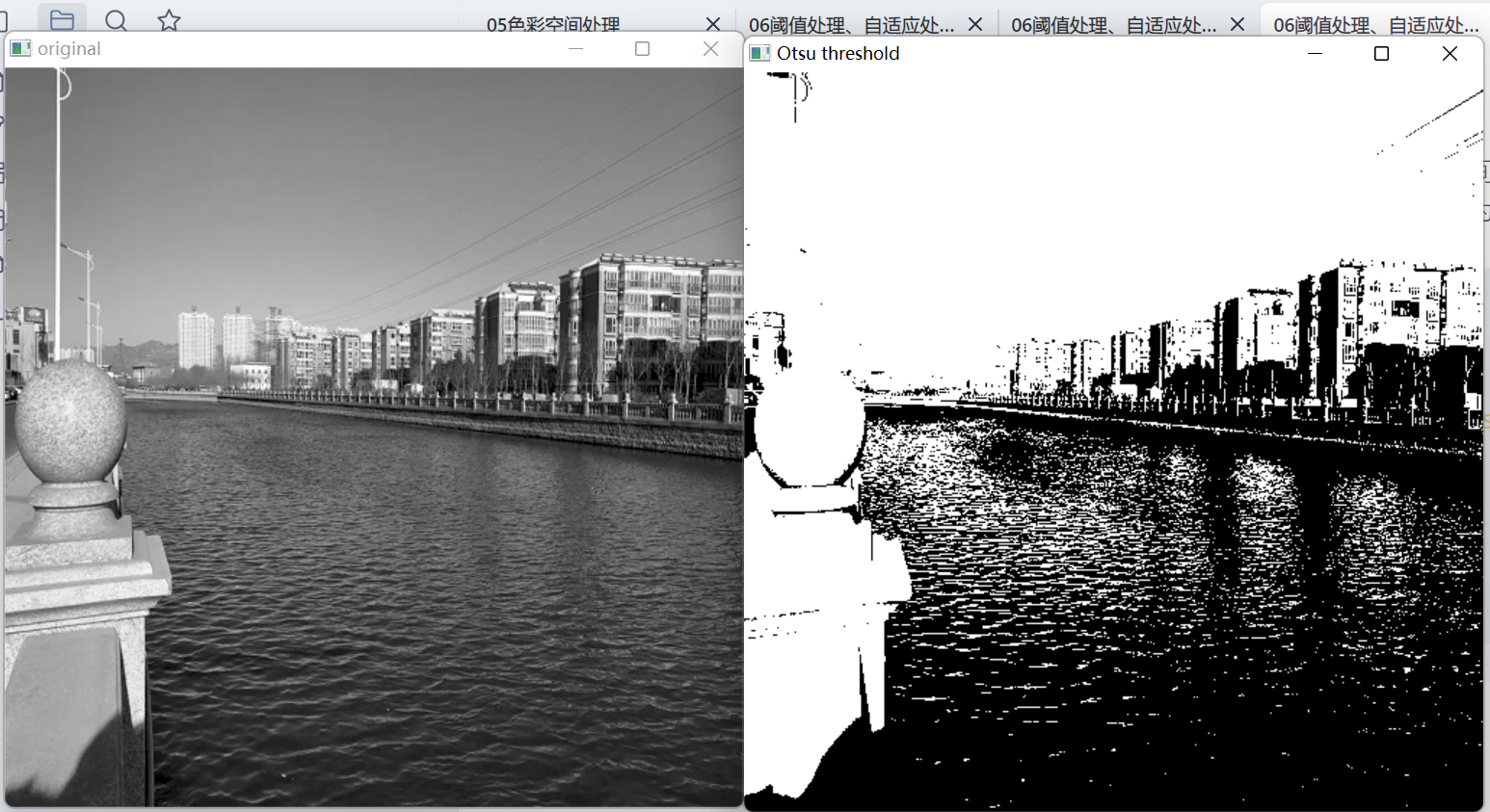
06 OpenCV 阈值处理、自适应处理与ostu方法
1 基本概念 CV2中使用阈值的作用是将灰度图像二值化,即将灰度图像的像素值根据一个设定的阈值分成黑白两部分。阈值处理可以用于图像分割、去除噪声、增强图像对比度等多个领域。例如,在物体检测和跟踪中,可以通过对图像进行阈值处理来提取目…...

RFC7519规范-JWT - json web token
简介 什么是JWT(JSON Web Token) 在介绍JWT之前,我们先来回顾一下利用token进行用户身份验证的流程: 客户端使用用户名和密码请求登录服务端收到请求,验证用户名和密码验证成功后,服务端会签发一个token,再把这个to…...

移动机器人设计与实践课程大纲
MiR移动机器人参考资料:图一 西北工业大学-课程平台图二 清华大学出版社-移动机器人目前,基本都是双一流大学开设此类课程,并且都是至少3-4学分,16学时/学分,48-64学时。(⊙﹏⊙),难办了。咱这只有…...
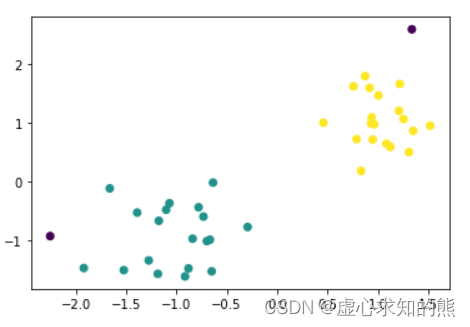
Lesson 7.2 Mini Batch K-Means与DBSCAN密度聚类
文章目录一、Mini Batch K-Means 算法原理与实现二、DBSCAN 密度聚类基本原理与实践1. K-Means 聚类算法的算法特性2. DBSCAN 密度聚类基本原理3. DBSCAN 密度聚类的 sklearn 实现除了 K-Means 快速聚类意外,还有两种常用的聚类算法。(1) 是能…...

11.Dockerfile最佳实践
Dockerfile 最佳实践 Docker官方关于Dockerfile最佳实践原文链接地址:https://docs.docker.com/develop/develop-images/dockerfile_best-practices/ Docker 可以通过从 Dockerfile 包含所有命令的文本文件中读取指令自动构建镜像,以便构建给定镜像。 …...
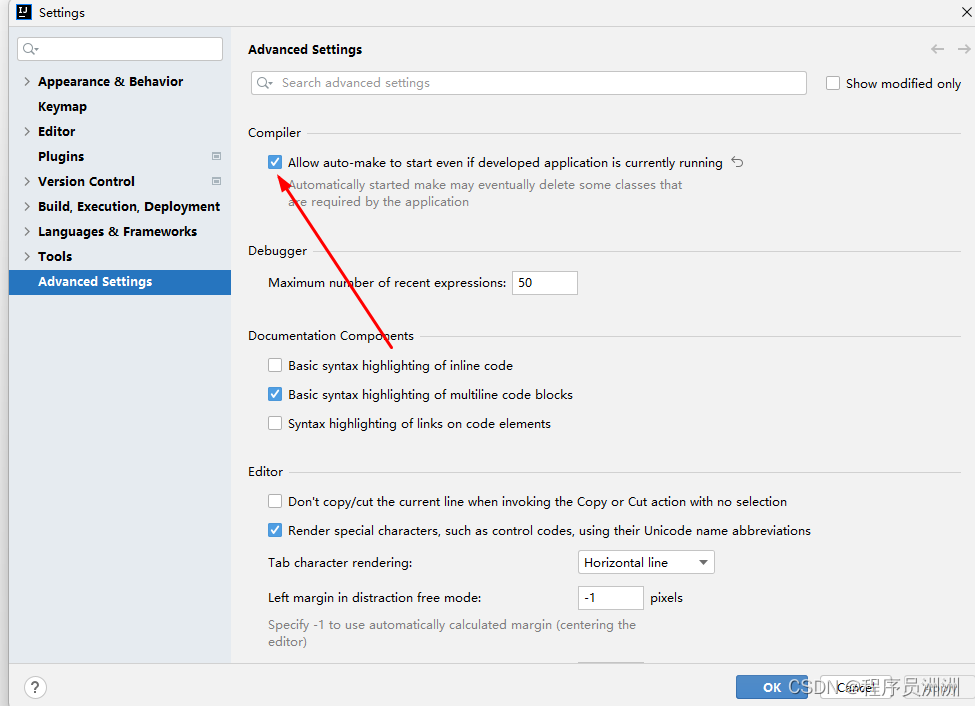
【企业云端全栈开发实践-1】项目介绍及环境准备、Spring Boot快速上手
本节目录一、 项目内容介绍二、Maven介绍2.1 Maven作用2.2 Maven依赖2.3 本地仓库配置三、Spring Boot快速上手3.1 Spring Boot特点3.2 遇到的Bug:spring-boot-maven-plugin3.3 遇到的Bug2:找不到Getmapping四、开发环境热部署一、 项目内容介绍 本课程…...
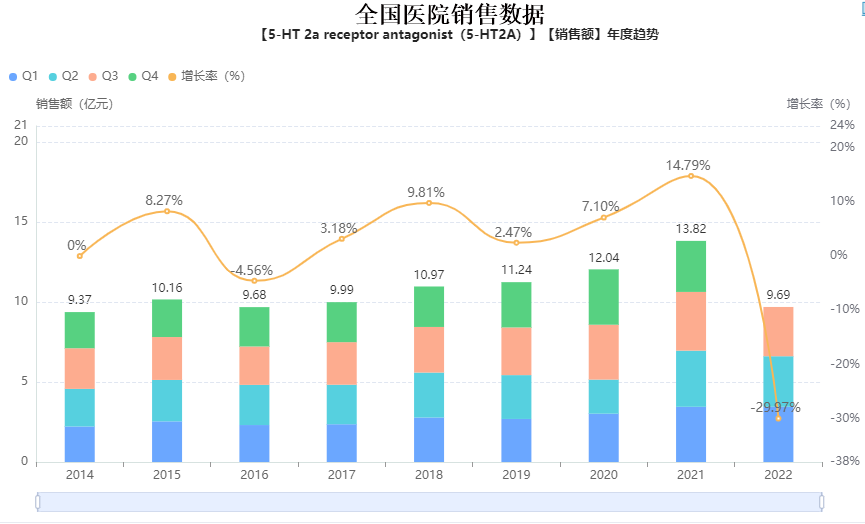
5-HT2A靶向药物|适应症|市场销售-上市药品前景分析
据世界卫生组织称,抑郁症是一种多因素疾病,影响全球约3.5 亿人。中枢神经系统最广泛的单胺 - 血清素 (5-HT) 被认为在这种情况的病理机制中起着至关重要的作用,并且神经递质的重要性被“血清素假说”提升,将抑郁症的存在联系起来 …...

HTTPS协议原理---详解
目录 一、HTTPS 1.加密与解密 2.我们为什么要加密? 3.常见加密方式 ①对称加密 ②非对称加密 4.数据摘要 5.数字签名 二、HTTPS的加密方案 1.只是用对称加密 2.只使用非对称加密 3.双方都使用非对称加密 4.非对称加密+对称加密 中间人攻…...
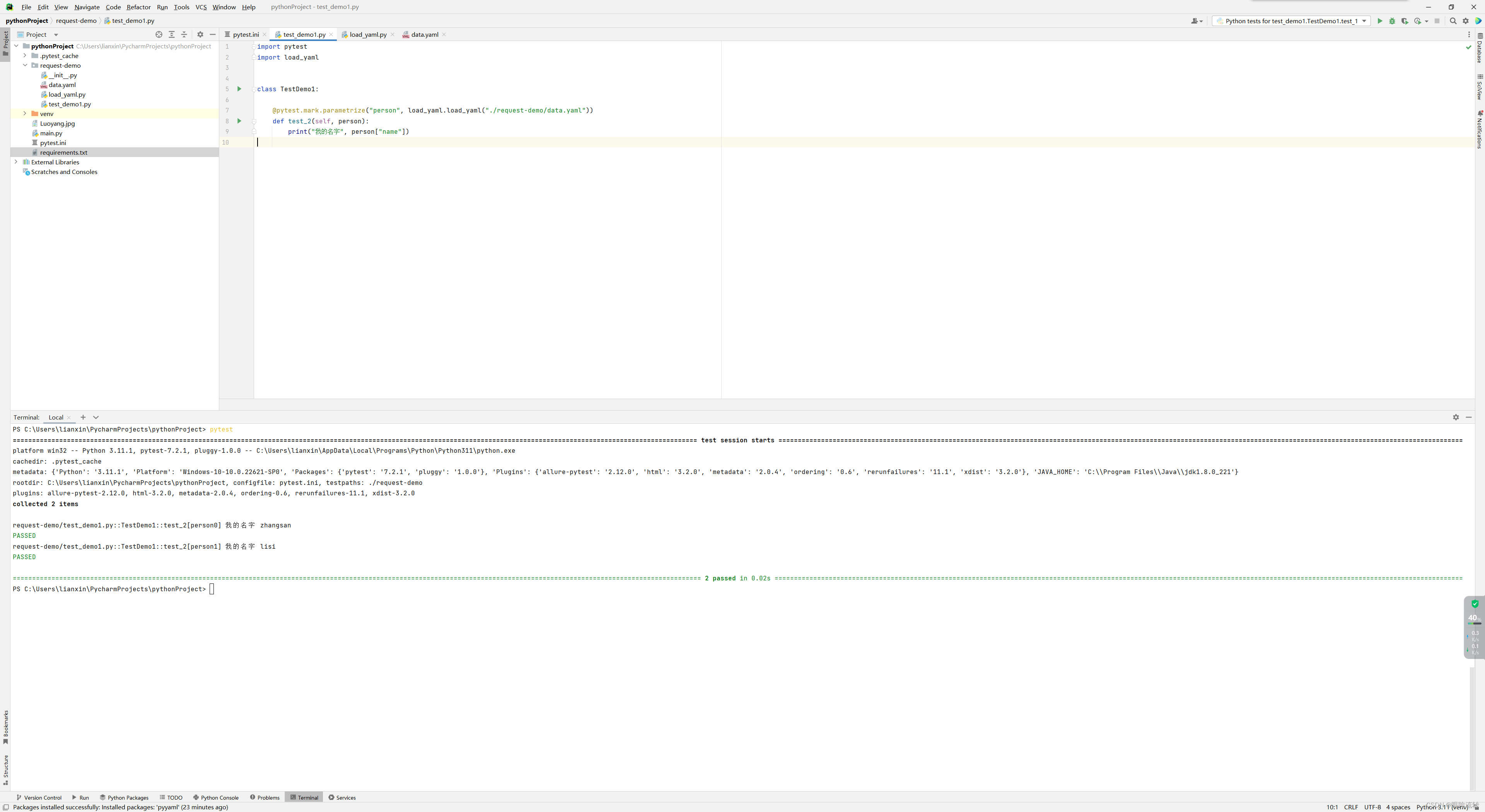
Pytest学习笔记
Pytest学习笔记 1、介绍 1.1、单元测试 单元测试是指在软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试 1.2、单元测试框架 测试发现:从多个py文件里面去找到我们测试用例测试执行:按…...
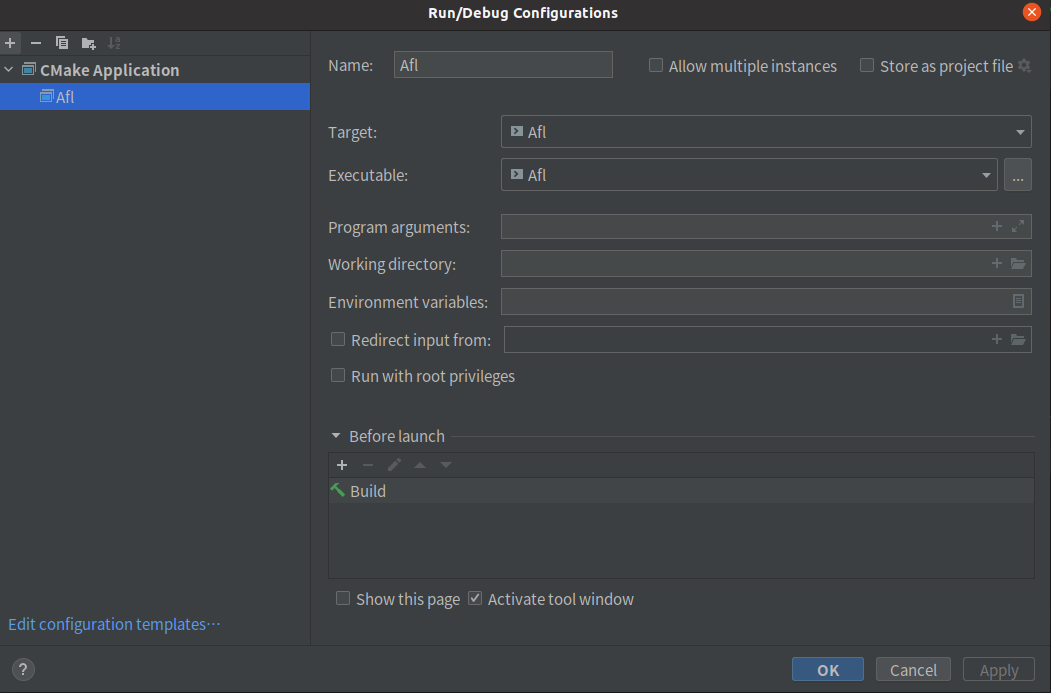
Fuzz概述
文章目录AFL一些概念插桩与覆盖率边和块覆盖率afl自实现劫持汇编器clang内置覆盖率反馈与引导变异遗传算法fork server机制AFL调试准备AFL一些概念 插桩与覆盖率 边和块 首先,要明白边和块的定义 正方形的就是块,箭头表示边,边表示程序执行…...
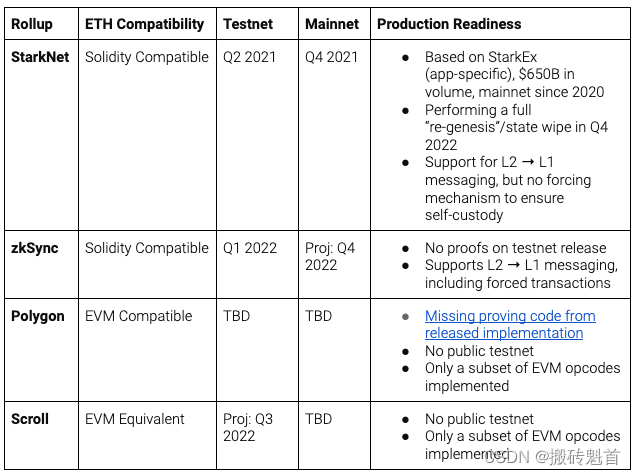
区块链知识系列 - 系统学习EVM(四)-zkEVM
区块链知识系列 - 系统学习EVM(一) 区块链知识系列 - 系统学习EVM(二) 区块链知识系列 - 系统学习EVM(三) 今天我们来聊聊 zkEVM、EVM 兼容性 和 Rollup 是什么? 1. 什么是 Rollup rollup顾名思义,就是把一堆交易卷(rollup)起来…...

Leetcode.2341 数组能形成多少数对
题目链接 Leetcode.2341 数组能形成多少数对 Rating : 1185 题目描述 给你一个下标从 0 开始的整数数组 nums。在一步操作中,你可以执行以下步骤: 从 nums选出 两个 相等的 整数从 nums中移除这两个整数,形成一个 数对 请你在 nums上多次执…...

C++复习笔记10
1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向其前一个元素和后一个元素。 3. list与for…...
leaflet 纯CSS的marker标记,不用图片来表示(072)
第072个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用纯CSS来打造marker的标记。这里用到的是L.divIcon来引用CSS来构造新icon,然后在marker的属性中引用。 这里必须要注意的是css需要是全局性质的,不能被scoped转义为其他随机的css。 直接复制下面的 v…...
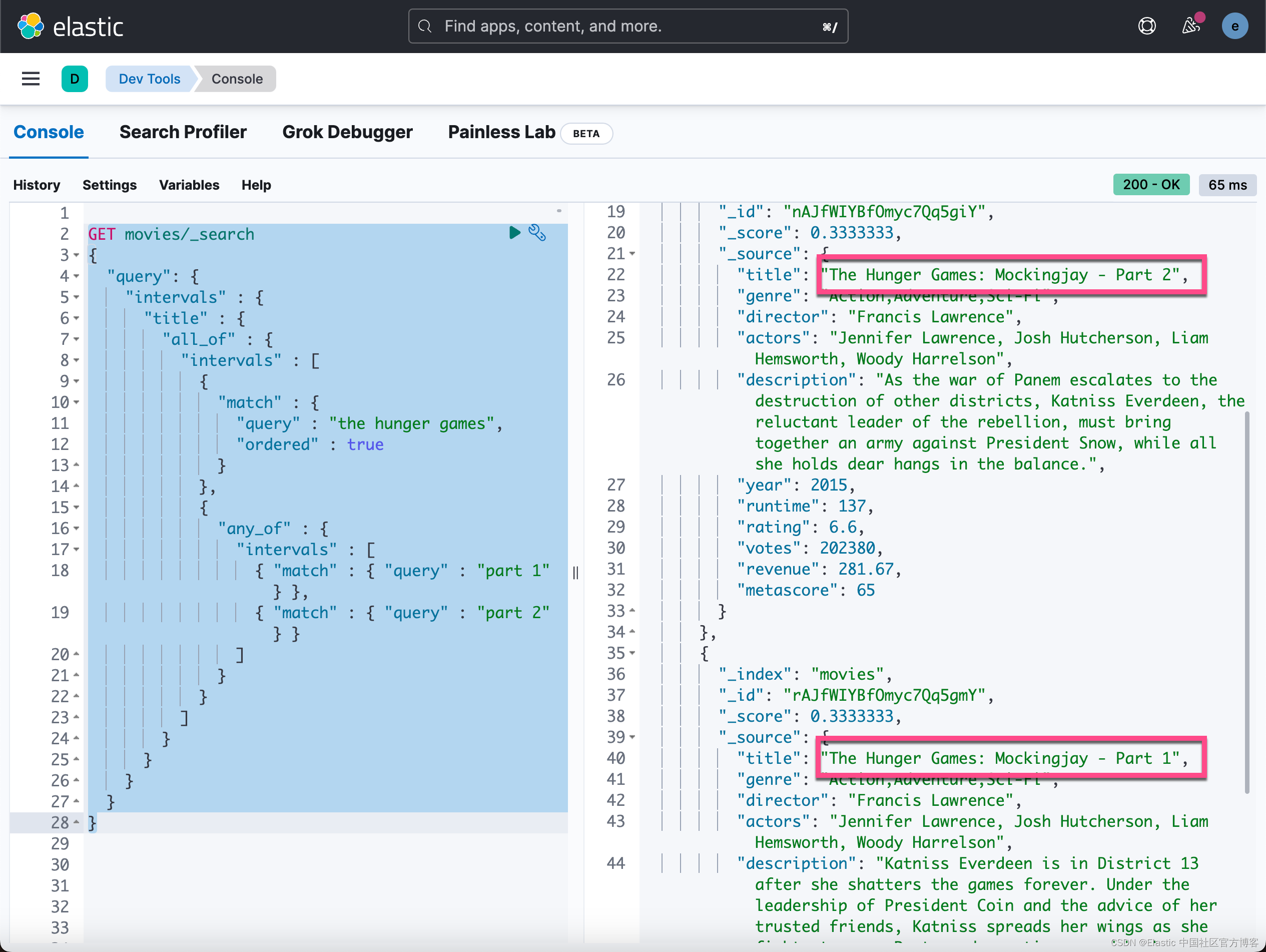
Elasticsearch:使用 intervals query - 根据匹配项的顺序和接近度返回文档
Intervals query 根据匹配项的顺序和接近度返回文档。Intervals 查询使用匹配规则,由一小组定义构成。 然后将这些规则应用于指定字段中的术语。 这些定义产生跨越文本正文中的术语的最小间隔序列。 这些间隔可以通过父源进一步组合和过滤。 上述描述有点费解。我…...
无法决定博客主题的人必看!如何选择类型和推荐的 5 种选择
是否有人不能迈出第一步,因为博客的类型还没有决定?有些人在出发时应该行动,而不是思考,但让我们冷静下来,仔细想想。博客的难度因流派而异,这在很大程度上决定了随后的发展。因此,在选择博客流…...
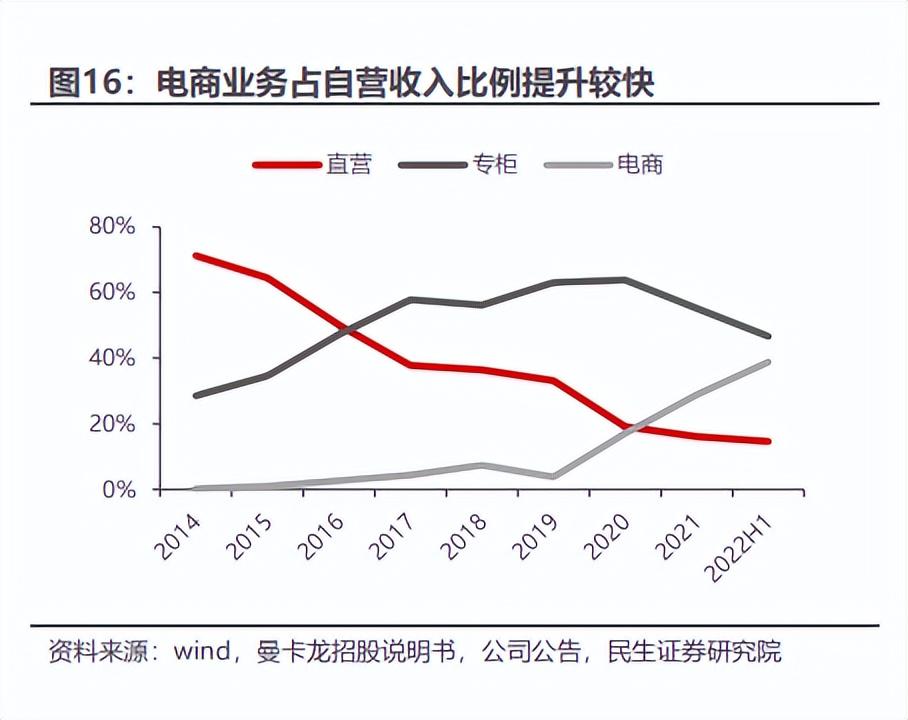
数字化转型的成功模版,珠宝龙头曼卡龙做对了什么?
2月11日,曼卡龙(300945.SZ)发布2022年业绩快报,报告期内,公司实现营业收入16.11亿元,同比增长28.63%。来源:曼卡龙2022年度业绩快报曼卡龙能在2022年实现营收增长尤为不易。2022年受疫情影响&am…...
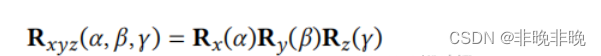
转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录1. 转换矩阵、平移矩阵、旋转矩阵之间的关系2. 缩放变换、平移变换和旋转变换2. python实现旋转矩阵、四元数、欧拉角互相转化由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...

LTR-381RGB-01RGB+环境光检测应用场景及客户类型主要有哪些?
RGB环境光检测 功能,在应用场景及客户类型: 1. 可应用的儿童玩具类型 (1) 智能互动玩具 功能:通过检测环境光或物体颜色触发互动(如颜色识别积木、光感音乐盒)。 客户参考: LEGO(乐高&#x…...
