[足式机器人]Part3机构运动微分几何学分析与综合Ch01-4 平面运动微分几何学——【读书笔记】
本文仅供学习使用
本文参考:
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任
Ch01-4 平面运动微分几何学
- 1.2.3-2 点轨迹的Euler-Savary公式
- 1.2.4 高阶曲率理论
1.2.3-2 点轨迹的Euler-Savary公式
例1-7: 平面曲柄摇杆机构的 Euler-Savary公式。
在例1-5中给出了平面曲柄摇杆机构动瞬心线πm{{\pi }_{m}}πm与定瞬心线πf{{\pi }_{f}}πf,动瞬心线πm{{\pi }_{m}}πm上的Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}可由式(1.47)得到∶
{R⃗m=1ka−θ˙(−sinθi⃗m+cosθj⃗m)E⃗1m=−[θ˙(ka−θ˙)cosθ+θ¨sinθ]i⃗m+[−θ˙(ka−θ˙)sinθ+θ¨cosθ]j⃗m[θ˙2(ka−θ˙)2+θ¨2]12E⃗2m=[θ˙(ka−θ˙)sinθ−θ¨cosθ]i⃗m−[θ˙(ka−θ˙)cosθ+θ¨sinθ]j⃗m[θ˙2(ka−θ˙)2+θ¨2]12\left\{ \begin{matrix} {{{\vec{R}}}_{m}}=\frac{1}{{{k}_{a}}-\dot{\theta }}(-\sin \theta {{{\vec{i}}}_{m}}+\cos \theta {{{\vec{j}}}_{m}}) \\ {{{\vec{E}}}_{1m}}=\frac{-[\dot{\theta }({{k}_{a}}-\dot{\theta })\cos \theta +\ddot{\theta }\sin \theta ]{{{\vec{i}}}_{m}}+[-\dot{\theta }({{k}_{a}}-\dot{\theta })\sin \theta +\ddot{\theta }\cos \theta ]{{{\vec{j}}}_{m}}}{{{[{{{\dot{\theta }}}^{2}}{{({{k}_{a}}-\dot{\theta })}^{2}}+{{{\ddot{\theta }}}^{2}}]}^{\frac{1}{2}}}} \\ {{{\vec{E}}}_{2m}}=\frac{[\dot{\theta }({{k}_{a}}-\dot{\theta })\sin \theta -\ddot{\theta }\cos \theta ]{{{\vec{i}}}_{m}}-[\dot{\theta }({{k}_{a}}-\dot{\theta })\cos \theta +\ddot{\theta }\sin \theta ]{{{\vec{j}}}_{m}}}{{{[{{{\dot{\theta }}}^{2}}{{({{k}_{a}}-\dot{\theta })}^{2}}+{{{\ddot{\theta }}}^{2}}]}^{\frac{1}{2}}}} \\ \end{matrix} \right.⎩⎨⎧Rm=ka−θ˙1(−sinθim+cosθjm)E1m=[θ˙2(ka−θ˙)2+θ¨2]21−[θ˙(ka−θ˙)cosθ+θ¨sinθ]im+[−θ˙(ka−θ˙)sinθ+θ¨cosθ]jmE2m=[θ˙2(ka−θ˙)2+θ¨2]21[θ˙(ka−θ˙)sinθ−θ¨cosθ]im−[θ˙(ka−θ˙)cosθ+θ¨sinθ]jm
对于由r+Dsinα=0r+D\sin \alpha =0r+Dsinα=0确定的连杆平面上的拐点圆,可以通过上式将其转换到连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中描述为∶
(xm−a)2+(ym−b)2=D24{{({{x}_{m}}-a)}^{2}}+{{({{y}_{m}}-b)}^{2}}=\frac{{{D}^{2}}}{4}(xm−a)2+(ym−b)2=4D2
其中拐点圆圆心坐标(a,b)(a,b)(a,b)为∶
{a=−θ¨cosθ+(2ka−θ˙)(ka−θ˙)sinθ2(ka−θ˙)3b=θ¨sinθ+(2ka−θ˙)(ka−θ˙)cosθ2(ka−θ˙)3\left\{ \begin{matrix} a=-\frac{\ddot{\theta }\cos \theta +(2{{k}_{a}}-\dot{\theta })({{k}_{a}}-\dot{\theta })\sin \theta }{2{{({{k}_{a}}-\dot{\theta })}^{3}}} \\ b=\frac{\ddot{\theta }\sin \theta +(2{{k}_{a}}-\dot{\theta })({{k}_{a}}-\dot{\theta })\cos \theta }{2{{({{k}_{a}}-\dot{\theta })}^{3}}} \\ \end{matrix} \right.⎩⎨⎧a=−2(ka−θ˙)3θ¨cosθ+(2ka−θ˙)(ka−θ˙)sinθb=2(ka−θ˙)3θ¨sinθ+(2ka−θ˙)(ka−θ˙)cosθ
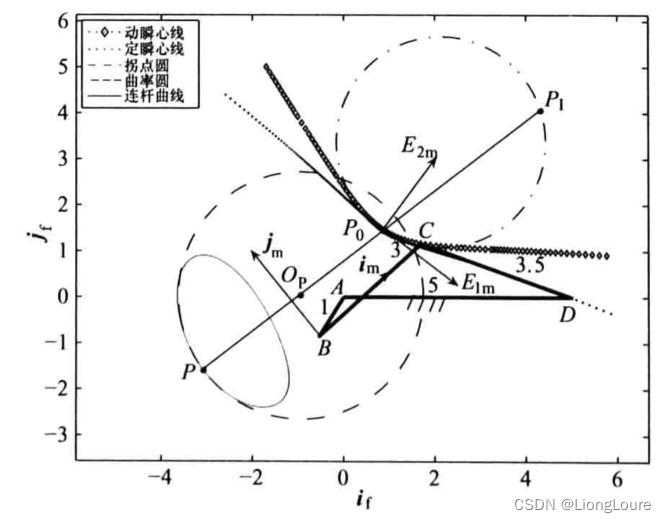
当该曲柄摇杆机构的输入角φ=238∘\varphi =238{}^\circφ=238∘时,瞬心点P0{{P}_{0}}P0在连杆坐标系中的极坐标为rP0=2.6995,θP0=15.9604∘{{r}_{{{P}_{0}}}}=\text{2}\text{.6995},{{\theta }_{{{P}_{0}}}}=\text{15}\text{.9604}{}^\circrP0=2.6995,θP0=15.9604∘,定瞬心线πf{{\pi }_{f}}πf与动瞬心线πm{{\pi }_{m}}πm的曲率分别为kf=0.3712,km=0.5892{{k}_{f}}=\text{0}\text{.3712,}{{k}_{m}}=\text{0}\text{.5892}kf=0.3712,km=0.5892,从而诱导曲率k*=kf−km=−0.2180k\text{*=}{{k}_{f}}-{{k}_{m}}=-\text{0}\text{.2180}k*=kf−km=−0.2180。代人式(1.74b),得到此时的Euler-Savary公式为∶
ρΓ(r−sinα0.2180)=r2{{\rho }_{\Gamma }}\text{(}r-\frac{\sin \alpha }{\text{0}\text{.2180}}\text{)=}{{r}^{\text{2}}}ρΓ(r−0.2180sinα)=r2
此时连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中的拐点圆方程为∶
(xm−4.8075)2+(ym−1.3502)2=5.2627{{({{x}_{m}}-4.8075)}^{2}}+{{({{y}_{m}}-1.3502)}^{2}}=5.2627(xm−4.8075)2+(ym−1.3502)2=5.2627
连杆上的一点PPP在Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中的极坐标为(5,250∘)(5,250{}^\circ )(5,250∘),其在连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中的直角坐标为(−2.3882,1.1463)(-2.3882,1.1463)(−2.3882,1.1463),则可由Euler-Savary公式得到其轨迹曲线ΓP{{\Gamma }_{P}}ΓP,在该瞬时的曲率半径ρΓ=2.6849{{\rho }_{\Gamma }}=2.6849ρΓ=2.6849,从而可知曲率中心OP{{O}_{P}}OP在Frenet标架{R⃗f;E⃗1f,E⃗2f}\{{{{\vec{R}}}_{f}};{{{\vec{E}}}_{1f}},{{{\vec{E}}}_{2f}}\}{Rf;E1f,E2f}中的极坐标(rOP=2.3151,αOP=250∘{{r}_{{{O}_{P}}}}=\text{2}\text{.3151},{{\alpha }_{{{O}_{P}}}}=\text{250}{}^\circrOP=2.3151,αOP=250∘),或者在固定坐标系{A;i⃗f,j⃗f}\{A;{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}{A;if,jf}中的直角坐标为(−0.9384,0.0349)(-0.9384,0.0349)(−0.9384,0.0349)。此时,拐点PI{{P}_{I}}PI在Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中的极坐标为(4.3114,70∘)(4.3114,70{}^\circ )(4.3114,70∘),在连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中的直角坐标为(6.8928,0.3940)(6.8928,0.3940)(6.8928,0.3940)。将所有特征点的坐标均转换到固定坐标系中描述,结果如下图所示。
例1-8: 平面曲柄滑块机构的Euler-Savary公式。
在例1-6中给出了平面曲柄滑块机构动瞬心线πm{{\pi }_{m}}πm与定瞬心线πf{{\pi }_{f}}πf,动瞬心线πm{{\pi }_{m}}πm上的Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}可同样采用式(E1-7.1)得到。利用式(E1-7.2)和式(E1-7.3)可以得到连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中拐点圆的方程。
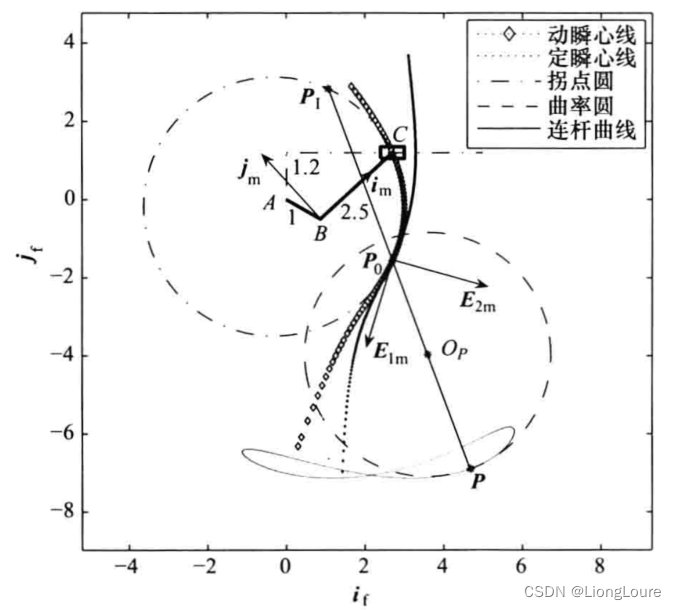
当曲柄滑块机构的输入角为φ=−30∘\varphi =-30{}^\circφ=−30∘时,瞬心点P0{{P}_{0}}P0在连杆坐标系中的极坐标为rP0=2.1166,θP0=−72.8463∘{{r}_{{{P}_{0}}}}=2.1166,{{\theta }_{{{P}_{0}}}}=-72.8463{}^\circrP0=2.1166,θP0=−72.8463∘,定瞬心线πf{{\pi }_{f}}πf与动瞬心线πm{{\pi }_{m}}πm的曲率分别为kf=−0.1076,km=−0.2585{{k}_{f}}=-0.1076,{{k}_{m}}=-0.2585kf=−0.1076,km=−0.2585,从而诱导曲率k*=kf−km=0.1509k\text{*=}{{k}_{f}}-{{k}_{m}}=0.1509k*=kf−km=0.1509。代入式(1.74b),得到此时的Euler-Savary公式∶
ρΓ(r+sinα0.1509)=r2{{\rho }_{\Gamma }}\text{(}r+\frac{\sin \alpha }{\text{0}\text{.1509}}\text{)=}{{r}^{\text{2}}}ρΓ(r+0.1509sinα)=r2
此时连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中的拐点圆方程为∶
(xm+0.6465)2+(ym−1.0372)2=10.9760{{({{x}_{m}}+0.6465)}^{2}}+{{({{y}_{m}}-1.0372)}^{2}}=10.9760(xm+0.6465)2+(ym−1.0372)2=10.9760
连杆上的一点PPP在Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中的极坐标为(5.7,45∘)(5.7,45{}^\circ )(5.7,45∘),其在连杆坐标系 {B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中的直角坐标为(−1.5518,−7.2907)(-1.5518,-7.2907)(−1.5518,−7.2907),则可由Euler-Savary公式得到PPP点轨迹曲线ΓP{{\Gamma }_{P}}ΓP在该瞬时对应点处的曲率半径ρΓ=3.1285{{\rho }_{\Gamma }}=3.1285ρΓ=3.1285,从而可知曲率中心OP{{O}_{P}}OP在Frenet标架{R⃗f;E⃗1f,E⃗2f}\{{{{\vec{R}}}_{f}};{{{\vec{E}}}_{1f}},{{{\vec{E}}}_{2f}}\}{Rf;E1f,E2f}中的极坐标为(rOP=2.5715,αOP=45∘{{r}_{{{O}_{P}}}}=2.5715,{{\alpha }_{{{O}_{P}}}}=\text{45}{}^\circrOP=2.5715,αOP=45∘),以及在固定坐标系{A;i⃗f,j⃗f}\{A;{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}{A;if,jf}中的直角坐标为(3.5954,−3.9686)(3.5954,-3.9686)(3.5954,−3.9686)。此时,拐点PI{{P}_{I}}PI在Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中的极坐标为(4.6853,225∘)(4.6853,225{}^\circ )(4.6853,225∘),在连杆坐标系{B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{B;im,jm}中的直角坐标为(2.4131,2.3080)(2.4131,2.3080)(2.4131,2.3080)。将所有特征点的坐标均转换到固定坐标系中描述,结果如下图所示。
1.2.4 高阶曲率理论
平面曲线在一点的曲率只能反映该曲线在该点邻近三个无限接近位置处的几何性质。因而,为获得曲线在该点更大邻域内的几何性质,需要对曲率的高阶导数进行研究。例如,当连杆点的轨迹在某点曲率的一阶导数为特定的值(如零),表明轨迹曲线具有特定的几何意义,在机构学上研究这些点的位置,对机构的分析和综合具有重要的指导意义。
将kΓ=r+sinα/k∗r2{{k}_{\Gamma }}=\frac{r+\sin \alpha /k*}{{{r}^{2}}}kΓ=r2r+sinα/k∗对弧长参数σ\sigmaσ分别进行一次求导以及二次求导可得到∶
dkΓdσ=1H(1Msinα+1Ncosα−1r)\frac{d{{k}_{\Gamma }}}{d\sigma }=\frac{1}{H}(\frac{1}{M\sin \alpha }+\frac{1}{N\cos \alpha }-\frac{1}{r})dσdkΓ=H1(Msinα1+Ncosα1−r1)
d2kΓdσ2=(T−1HdHdσ)dk∗dσ−Hcosα(dk∗dσ)2+1HRQ\frac{{{d}^{2}}{{k}_{\Gamma }}}{d{{\sigma }^{2}}}=(T-\frac{1}{H}\frac{dH}{d\sigma })\frac{dk*}{d\sigma }-H\cos \alpha {{(\frac{dk*}{d\sigma })}^{2}}+\frac{1}{H}RQdσ2d2kΓ=(T−H1dσdH)dσdk∗−Hcosα(dσdk∗)2+H1RQ
式中:
{1H=−3sinαcosαr2k∗,1M=km−k∗3,1N=13k∗dk∗dσ,T=3Mcotα+1N(2−tan2α)R=1N2cosαsin2α,Q=tan4α+c1tan3α+c2tan2α+c3tanα+c4c1=−kmN+NM,c2=−(1+dNdσ),c3=NM2(dMdσN+3M),c3=(Mkm−2)N2M2\left\{ \begin{matrix} \frac{1}{H}=-\frac{3\sin \alpha \cos \alpha }{{{r}^{2}}k*},\frac{1}{M}=\frac{{{k}_{m}}-k*}{3},\frac{1}{N}=\frac{1}{3k*}\frac{dk*}{d\sigma },T=\frac{3}{M}\cot \alpha +\frac{1}{N}(2-{{\tan }^{2}}\alpha ) \\ R=\frac{1}{{{N}^{2}}}\frac{\cos \alpha }{{{\sin }^{2}}\alpha },Q={{\tan }^{4}}\alpha +{{c}_{1}}{{\tan }^{3}}\alpha +{{c}_{2}}{{\tan }^{2}}\alpha +{{c}_{3}}\tan \alpha +{{c}_{4}} \\ {{c}_{1}}=-{{k}_{m}}N+\frac{N}{M},{{c}_{2}}=-(1+\frac{dN}{d\sigma }),{{c}_{3}}=\frac{N}{{{M}^{2}}}(\frac{dM}{d\sigma }N+3M),{{c}_{3}}=\frac{(M{{k}_{m}}-2){{N}^{2}}}{{{M}^{2}}} \\ \end{matrix} \right.⎩⎨⎧H1=−r2k∗3sinαcosα,M1=3km−k∗,N1=3k∗1dσdk∗,T=M3cotα+N1(2−tan2α)R=N21sin2αcosα,Q=tan4α+c1tan3α+c2tan2α+c3tanα+c4c1=−kmN+MN,c2=−(1+dσdN),c3=M2N(dσdMN+3M),c3=M2(Mkm−2)N2
详细推导:
已知:drdσ=−cosα,dαdσ=−km+sinαr,kΓ=1r+sinαr2k∗\frac{dr}{d\sigma }=-\cos \alpha ,\frac{d\alpha }{d\sigma }=-{{k}_{m}}+\frac{\sin \alpha }{r},{{k}_{\Gamma }}=\frac{1}{r}+\frac{\sin \alpha }{{{r}^{2}}k*}dσdr=−cosα,dσdα=−km+rsinα,kΓ=r1+r2k∗sinα
{dkΓdσ=cosαr2+cosαdαdσr2k∗−sinα(2rdrdσk∗+r2dk∗dσ)r4k∗2=cosαr2+cosα(−km+sinαr)rk∗−sinα(−2cosαk∗+rdk∗dσ)r3k∗2=cosαr2+−rk∗kmcosα+sinαcosαk∗+2sinαcosαk∗−rsinαdk∗dσ)r3k∗2=rk∗2cosα−rk∗kmcosα+3sinαcosαk∗−rsinαdk∗dσ)r3k∗2=−3sinαcosαr2k∗(rk∗km3sinα−rk∗23sinα−k∗+rdk∗dσ3cosαrk∗)=1H(1Msinα+1Ncosα−1r)\left\{ \begin{matrix} \frac{d{{k}_{\Gamma }}}{d\sigma }=\frac{\cos \alpha }{{{r}^{2}}}+\frac{\cos \alpha \frac{d\alpha }{d\sigma }{{r}^{2}}k*-\sin \alpha (2r\frac{dr}{d\sigma }k*+{{r}^{2}}\frac{dk*}{d\sigma })}{{{r}^{4}}k{{*}^{2}}} \\ =\frac{\cos \alpha }{{{r}^{2}}}+\frac{\cos \alpha (-{{k}_{m}}+\frac{\sin \alpha }{r})rk*-\sin \alpha (-2\cos \alpha k*+r\frac{dk*}{d\sigma })}{{{r}^{3}}k{{*}^{2}}} \\ =\frac{\cos \alpha }{{{r}^{2}}}+\frac{-rk*{{k}_{m}}\cos \alpha +\sin \alpha \cos \alpha k*+2\sin \alpha \cos \alpha k*-r\sin \alpha \frac{dk*}{d\sigma })}{{{r}^{3}}k{{*}^{2}}} \\ \begin{matrix} =\frac{rk{{*}^{2}}\cos \alpha -rk*{{k}_{m}}\cos \alpha +3\sin \alpha \cos \alpha k*-r\sin \alpha \frac{dk*}{d\sigma })}{{{r}^{3}}k{{*}^{2}}} \\ =-\frac{3\sin \alpha \cos \alpha }{{{r}^{2}}k*}(\frac{\frac{rk*{{k}_{m}}}{3\sin \alpha }-\frac{rk{{*}^{2}}}{3\sin \alpha }-k*+\frac{r\frac{dk*}{d\sigma }}{3\cos \alpha }}{rk*}) \\ =\frac{1}{H}(\frac{1}{M\sin \alpha }+\frac{1}{N\cos \alpha }-\frac{1}{r}) \\ \end{matrix} \\ \end{matrix} \right.⎩⎨⎧dσdkΓ=r2cosα+r4k∗2cosαdσdαr2k∗−sinα(2rdσdrk∗+r2dσdk∗)=r2cosα+r3k∗2cosα(−km+rsinα)rk∗−sinα(−2cosαk∗+rdσdk∗)=r2cosα+r3k∗2−rk∗kmcosα+sinαcosαk∗+2sinαcosαk∗−rsinαdσdk∗)=r3k∗2rk∗2cosα−rk∗kmcosα+3sinαcosαk∗−rsinαdσdk∗)=−r2k∗3sinαcosα(rk∗3sinαrk∗km−3sinαrk∗2−k∗+3cosαrdσdk∗)=H1(Msinα1+Ncosα1−r1)
-
(1)曲率驻点 当运动刚体Σ*\Sigma \text{*}Σ*上点PPP轨迹曲线ΓP{{\Gamma }_{\text{P}}}ΓP的曲率kΓ{{k}_{\Gamma }}kΓ对弧长参数σ\sigmaσ的一阶导数为零时,表示该点轨迹此时曲率变化率为零,称其为
曲率驻点。令式(1.76)为零,可化简得∶
1r=1Msinα+1Nsinα\frac{1}{r}=\frac{1}{M\sin \alpha }+\frac{1}{N\sin \alpha }r1=Msinα1+Nsinα1
上式在瞬心线的Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中描述,可通过Frenet标架到运动坐标系{O⃗m;i⃗m,j⃗m}\{{{{\vec{O}}}_{m}};{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{Om;im,jm}的坐标变换将其转换到运动坐标系中描述,可得到关于点坐标(xPm,yPm)({{x}_{Pm}},{{y}_{Pm}})(xPm,yPm)的三次代数方程。将满足该方程的曲线称为刚体平面上的曲率驻点曲线,刚体上满足曲率驻点条件的点都分布在这条曲线上。曲率驻点无限接近四个位置均在一圆上,或者说其轨迹曲线在该点处与圆三阶接触。随着刚体的运动(对所有时刻σ\sigmaσ)刚体平面上的曲率驻点曲线形成曲线族。 -
(2)Ball点 当运动刚体Σ*\Sigma \text{*}Σ*上点的轨迹曲线的曲率kΓ{{k}_{\Gamma }}kΓ及其一阶导数dkΓ/dσd{{k}_{\Gamma }}/d\sigmadkΓ/dσ同时为零,即
式(1.75)与式(1.79)联立,得到该点在Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中极坐标(r,α)(r,\alpha )(r,α)满足的方程为∶
{tanα=k∗(km+2k∗)dk∗/dσr=−sinαk∗\left\{ \begin{matrix} \tan \alpha =\frac{k*({{k}_{m}}+2k*)}{dk*/d\sigma } \\ r=-\frac{\sin \alpha }{k*} \\ \end{matrix} \right.{tanα=dk∗/dσk∗(km+2k∗)r=−k∗sinα
该点为拐点圆与曲率驻点曲线的交点,称为Ball点。由1.1.2节可知,平面运动刚体上Ball 点的轨迹曲线在该点的四个无限接近位置共一直线,或与直线三阶接触。 -
(3)Burmester点 当运动刚体Σ*\Sigma \text{*}Σ*上点的轨迹曲线的曲率一阶导数dkΓ/dσd{{k}_{\Gamma }}/d\sigmadkΓ/dσ、二阶导数d2kΓ/dσ2{{d}^{2}}{{k}_{\Gamma }}/d{{\sigma }^{2}}d2kΓ/dσ2同时为零,则由
式(1.76)和式(1.77)得到该点在Frenet标架{R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}{Rm;E1m,E2m}中极坐标(r,α)(r,\alpha )(r,α)满足的方程为∶
{1r=1Msinα+1Nsinαtan4α+c1tan3α+c2tan2α+c3tanα+c4=0\left\{ \begin{matrix} \frac{1}{r}=\frac{1}{M\sin \alpha }+\frac{1}{N\sin \alpha } \\ {{\tan }^{4}}\alpha +{{c}_{1}}{{\tan }^{3}}\alpha +{{c}_{2}}{{\tan }^{2}}\alpha +{{c}_{3}}\tan \alpha +{{c}_{4}}=0 \\ \end{matrix} \right.{r1=Msinα1+Nsinα1tan4α+c1tan3α+c2tan2α+c3tanα+c4=0
式(1.81)中的第二式为tanα\tan \alphatanα 的四次方程,最多有四个实数解。将满足该方程式的刚体平面上的点称为Burmester 点,其在固定坐标系中的轨迹曲线在该点处的曲率同时满足dkΓ/dσ=0d{{k}_{\Gamma }}/d\sigma=0dkΓ/dσ=0和d2kΓ/dσ2=0{{d}^{2}}{{k}_{\Gamma }}/d{{\sigma }^{2}}=0d2kΓ/dσ2=0。这表明轨迹曲线在该点的无限接近五位置均在一圆上,或者说轨迹曲线在该点与圆四阶接触。
Burmester点的推导单独令写文章进行推导,(待补充)
- (4)Ball点曲线及其奇点 由
式(1.80)可以得到每一瞬时(瞬心线弧长σ\sigmaσ处)运动刚体Σ*\Sigma \text{*}Σ*上的一个Ball点,当刚体经过平面运动后,运动刚体上在不同瞬时的 Ball 点集合就组成了运动刚体上的Ball点曲线,Ball点在Frenet标架中的坐标(r,α)(r,\alpha )(r,α)或者运动坐标系中的坐标(xPm,yPm({{x}_{Pm}},{{y}_{Pm}}(xPm,yPm]则为瞬心线弧长参数σ的函数,并满足式(1.80)。
对于刚体平面上运动坐标系{O⃗m;i⃗m,j⃗m}\{{{{\vec{O}}}_{m}};{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}{Om;im,jm} 中的一点P(xPm,yPm)P({{x}_{Pm}},{{y}_{Pm}})P(xPm,yPm),其轨迹曲线的曲率如式(1.74c)所描述∶
kΓ=F(xPm,yPm,s)G(xPm,yPm,s){{k}_{\Gamma }}=\frac{F({{x}_{Pm}},{{y}_{Pm}},s)}{G({{x}_{Pm}},{{y}_{Pm}},s)}kΓ=G(xPm,yPm,s)F(xPm,yPm,s)
式中,sss为原曲线ΓOm{{\Gamma }_{Om}}ΓOm的弧长,FFF和GGG为刚体上点坐标(xPm,yPm)({{x}_{Pm}},{{y}_{Pm}})(xPm,yPm)以及弧长sss的函数,如式(1.74c)所示。
将上式对弧长参数sss求导,并且令dkΓds=0\frac{d{{k}_{\Gamma }}}{ds}=0dsdkΓ=0,可得到:
dkΓds=1G(dFdsG−dGdsF)=0\frac{d{{k}_{\Gamma }}}{ds}=\frac{1}{G}(\frac{dF}{ds}G-\frac{dG}{ds}F)=0dsdkΓ=G1(dsdFG−dsdGF)=0
由上式同样可以得到如式(1.79)关于刚体上点坐标的三次代数方程。令式(1.82)为零,并结合上式可得到Ball点满足的条件式∶
F(xPm,yPm,s)=0,∂F∂s=0F({{x}_{Pm}},{{y}_{Pm}},s)=0,\frac{\partial F}{\partial s}=0F(xPm,yPm,s)=0,∂s∂F=0
对于原曲线ΓOm{{\Gamma }_{Om}}ΓOm弧长参数sss的一段区间,上式的前一式描述了刚体平面上的一组拐点圆,而后一式则为将拐点圆位置对弧长参数sss求导,由于FFF为(xPm,yPm)({{x}_{Pm}},{{y}_{Pm}})(xPm,yPm)和sss的函数,因而上式描述了该组拐点圆的包络线。
将式(1.74c)中FFF的表达式代入式(1.84),可得到两组解,其中一组为:
{xm=u1(1)cosθ−u2(1)sinθym=u1(1)sinθ+u2(1)cosθ\left\{ \begin{matrix} {{x}_{m}}={{u}_{1}}^{(1)}\cos \theta -{{u}_{2}}^{(1)}\sin \theta \\ {{y}_{m}}={{u}_{1}}^{(1)}\sin \theta +{{u}_{2}}^{(1)}\cos \theta \\ \end{matrix} \right.{xm=u1(1)cosθ−u2(1)sinθym=u1(1)sinθ+u2(1)cosθ
其中:u1(1)=0;u2(1)=1kOm−θ˙{{u}_{1}}^{(1)}=0;{{u}_{2}}^{(1)}=\frac{1}{{{k}_{Om}}-\dot{\theta }}u1(1)=0;u2(1)=kOm−θ˙1
另一组解为:
{xm=u1(2)cosθ−u2(2)sinθym=u1(2)sinθ+u2(2)cosθ\left\{ \begin{matrix} {{x}_{m}}={{u}_{1}}^{(2)}\cos \theta -{{u}_{2}}^{(2)}\sin \theta \\ {{y}_{m}}={{u}_{1}}^{(2)}\sin \theta +{{u}_{2}}^{(2)}\cos \theta \\ \end{matrix} \right.{xm=u1(2)cosθ−u2(2)sinθym=u1(2)sinθ+u2(2)cosθ
其中:
{u1(2)=Cθ˙(kOm−θ˙)−C2(k˙Om−θ¨)(1+C2)(kOm−θ˙)3u2(2)=1kOm−θ˙+Cθ˙(kOm−θ˙)+C2(k˙Om−θ¨)(1+C2)(kOm−θ˙)3C=θ˙(kOm−θ˙)2(k˙Om−θ¨)+θ˙2(kOm−θ˙)3(2kOm−θ˙)+(kOm−θ˙)2(k˙Om−θ¨)(2k˙Om−3θ¨)θ˙θ¨(kOm−θ˙)3+(kOm−θ˙)(k˙Om−θ¨)(k¨Om−dθ¨/ds)−2θ˙2(k˙Om−θ¨)(kOm−θ˙)2−3(k˙Om−θ¨)3\left\{ \begin{matrix} {{u}_{1}}^{(2)}=\frac{C\dot{\theta }({{k}_{Om}}-\dot{\theta })-{{C}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })}{(1+{{C}^{2}}){{({{k}_{Om}}-\dot{\theta })}^{3}}} \\ {{u}_{2}}^{(2)}=\frac{1}{{{k}_{Om}}-\dot{\theta }}+\frac{C\dot{\theta }({{k}_{Om}}-\dot{\theta })+{{C}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })}{(1+{{C}^{2}}){{({{k}_{Om}}-\dot{\theta })}^{3}}} \\ C=\frac{\dot{\theta }{{({{k}_{Om}}-\dot{\theta })}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })+{{{\dot{\theta }}}^{2}}{{({{k}_{Om}}-\dot{\theta })}^{3}}(2{{k}_{Om}}-\dot{\theta })+{{({{k}_{Om}}-\dot{\theta })}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })(2{{{\dot{k}}}_{Om}}-3\ddot{\theta })}{\dot{\theta }\ddot{\theta }{{({{k}_{Om}}-\dot{\theta })}^{3}}+({{k}_{Om}}-\dot{\theta })({{{\dot{k}}}_{Om}}-\ddot{\theta })({{{\ddot{k}}}_{Om}}-d\ddot{\theta }/ds)-2{{{\dot{\theta }}}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta }){{({{k}_{Om}}-\dot{\theta })}^{2}}-3{{({{{\dot{k}}}_{Om}}-\ddot{\theta })}^{3}}} \\ \end{matrix} \right.⎩⎨⎧u1(2)=(1+C2)(kOm−θ˙)3Cθ˙(kOm−θ˙)−C2(k˙Om−θ¨)u2(2)=kOm−θ˙1+(1+C2)(kOm−θ˙)3Cθ˙(kOm−θ˙)+C2(k˙Om−θ¨)C=θ˙θ¨(kOm−θ˙)3+(kOm−θ˙)(k˙Om−θ¨)(k¨Om−dθ¨/ds)−2θ˙2(k˙Om−θ¨)(kOm−θ˙)2−3(k˙Om−θ¨)3θ˙(kOm−θ˙)2(k˙Om−θ¨)+θ˙2(kOm−θ˙)3(2kOm−θ˙)+(kOm−θ˙)2(k˙Om−θ¨)(2k˙Om−3θ¨)
式(1.85)和式(1.86)描述了拐点圆族的两条包络线。式(1.85)同1.2.1节中的式(1.42),描述了刚体平面上的动瞬心线;式(1.86)则为Ball点曲线的另一种表达形式。注意这两条包络线并不是等距线,因为拐点圆的半径随拐点圆位置不同而变化。
对于刚体平面上Ball点曲线的几何性质进行讨论,式(1.84)给出了Ball点满足的条件,而式(1.86a)则给出了Ball点的具体位置方程,可以将其写为∶
xbm=xbm(s),ybm=ybm(s){{x}_{bm}}={{x}_{bm}}(s),{{y}_{bm}}={{y}_{bm}}(s)xbm=xbm(s),ybm=ybm(s)
如果某一瞬时Ball点曲线上出现奇点,则:
x˙bm=dxbmds=0,y˙bm=dybmds=0{{{\dot{x}}}_{bm}}=\frac{d{{x}_{bm}}}{ds}=0,{{{\dot{y}}}_{bm}}=\frac{d{{y}_{bm}}}{ds}=0x˙bm=dsdxbm=0,y˙bm=dsdybm=0
将式(1.84)的的隐函数对弧长参数sss求偏导,可得∶
{Fxbmx˙bm+Fybmy˙bm+Fs=0Fxxbmx˙bm+Fxybmy˙bm+Fss=0\left\{ \begin{matrix} {{F}_{{{x}_{bm}}}}{{{\dot{x}}}_{bm}}+{{F}_{{{y}_{bm}}}}{{{\dot{y}}}_{bm}}+{{F}_{s}}=0 \\ {{F}_{x{{x}_{bm}}}}{{{\dot{x}}}_{bm}}+{{F}_{x{{y}_{bm}}}}{{{\dot{y}}}_{bm}}+{{F}_{ss}}=0 \\ \end{matrix} \right.{Fxbmx˙bm+Fybmy˙bm+Fs=0Fxxbmx˙bm+Fxybmy˙bm+Fss=0
相关文章:
[足式机器人]Part3机构运动微分几何学分析与综合Ch01-4 平面运动微分几何学——【读书笔记】
本文仅供学习使用 本文参考: 《机构运动微分几何学分析与综合》-王德伦、汪伟 《微分几何》吴大任 Ch01-4 平面运动微分几何学1.2.3-2 点轨迹的Euler-Savary公式1.2.4 高阶曲率理论1.2.3-2 点轨迹的Euler-Savary公式 例1-7: 平面曲柄摇杆机构的 Euler-Sa…...

【每日一题Day120】LC2341数组能形成多少数对 | 哈希表 排序
数组能形成多少数对【LC2341】 给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤: 从 nums 选出 两个 相等的 整数从 nums 中 移除这两个整数,形成一个 数对 请你在 nums 上多次执行此操作直到无法继续执行。 返回一…...
win11/10+opencv3.x/4.x配置 VS2019方法(简单使用,亲测)
首先下载 opencv,去官网下载百度》输入opencv,点击opencv|home,进入官网。点击 “Library”---->Release点击 对应版本下的 window版本,点击 --安装--extract---》设置路径。这个就是把库文件扩展到指定的路径下,扩…...

HTTP协议---详细讲解
目录 一、HTTP协议 1.http 2.url url的组成: url的保留字符: 3.http协议格式编辑 ①http request ②http response 4.对request做出响应 5.GET与POST方法 ①GET ②POST 7.HTTP常见Header ①Content-Type:: 数据类型(text/html等)在上文…...

Syntax-Aware Aspect-Level Sentiment Classification with PWCN 论文阅读笔记
一、作者 Chen Zhang, Qiuchi Li, and Dawei Song. 2019. Syntax-Aware Aspect-Level Sentiment Classification with Proximity-Weighted Convolution Network. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information …...
hadoop考试应急
概述 四大特点:大量化、快速化、多元化、价值化 关键技术:采集、存储管理、处理分析、隐私和安全 计算模式:批处理、流、图、查询分析计算 Hadoop处理架构 了解就好 2007年,雅虎在Sunnyvale总部建立了M45——一个包含了4000…...

【React】Hooks
🚩🚩🚩 💎个人主页: 阿选不出来 💨💨💨 💎个人简介: 一名大二在校生,学习方向前端,不定时更新自己学习道路上的一些笔记. 💨💨💨 💎目…...

升级Room引发的惨案!!
kotlin升级 在升级kotlin的时候,直接升级到大版本的kotlin(比如1.7以上),直接报错,只是报错不知道原因。 koltin Release details 后来把koltin版本改成1.6.0,报如下的错,我们才知道gradle是需…...

RPC框架:一文带你搞懂RPC
RPC是什么(GPT答) ChatGPT回答: RPC(Remote Procedure Call)是一种分布式应用程序的编程模型,允许程序在不同的计算机上运行。它以一种透明的方式,将一个程序的函数调用定向到远程系统上的另一个程序,而使…...
电子招标采购系统源码—企业战略布局下的采购寻源
智慧寻源 多策略、多场景寻源,多种看板让寻源过程全程可监控,根据不同采购场景,采取不同寻源策略, 实现采购寻源线上化管控;同时支持公域和私域寻源。 询价比价 全程线上询比价,信息公开透明࿰…...
P16 激活函数与Loss 的梯度
参考:https://www.ngui.cc/el/507608.html?actiononClick这里面简单回顾一下PyTorch 里面的两个常用的梯度自动计算的APIautoGrad 和 Backward, 最后结合 softmax 简单介绍一下一下应用场景。目录:1 autoGrad2 Backward3 softmax一 autoGrad输入 x输出损…...
ThinkPHP5美食商城系统
有需要请私信或看评论链接哦 可远程调试 ThinkPHP5美食商城系统一 介绍 此美食商城系统基于ThinkPHP5框架开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。用户注册登录后可购买美食,个人中心,评论和反馈等ÿ…...
 / <script setup>))
Vue3 - $refs 使用教程,父组件调用获取子组件数据和方法(setup() / <script setup>)
前言 在 Vue2 中父组件使用 $refs 调用子组件数据和方法非常简单,但在 Vue3 中这种方法行不通了。 本文实现了 Vue3 中父组件使用 $refs 获取调用子组件数据和方法教程, 并且提供了 setup() 与 <script setup> 两种 “开发模式” 的示例代码,请根据需要进行选择。 网…...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 众数和中位数(Python)| 真题+思路+考点+代码+岗位
众数和中位数 题目 众数是指一组数据中出现次数多的数 众数可以是多个中位数是指把一组数据从小到大排列,最中间的那个数, 如果这组数据的个数是奇数,那最中间那个就是中位数 如果这组数据的个数为偶数,那就把中间的两个数之和除以 2 就是中位数查找整型数组中元素的众数并…...

一眼万年的 Keychron 无线机械键盘
一眼万年的 Keychron 无线机械键盘 一款好的键盘对于程序员或者喜欢码字的人来说是非常重要的,而最近博主入手了自己的第一款机械键盘——Keychron 无线机械键盘。 机械键盘特点 有独立轴体,通过两个簧接触,来触发信号,价格相对贵…...

自动化测试高频面试题(含答案)
Hello,你们的好朋友来了!今天猜猜我给大家带来点啥干货呢?最近很多小伙伴出去面试的时候经常会被问到跟自动化测试相关的面试题。所以,今天特意给大家整理了一些经常被公司问到的自动化测试相关的面试题。停,咱先收藏起…...

3、按键扫描检测处理
说明:本文处理按键的短按、长按检测执行,非矩阵按键 硬件可以类似如下连接即可,无需放置上下拉电阻; 按键动作分长按、短按(弹起时执行)两种 按下不放执行长按,但松开按键时不予执行短按函数 多个按键可以同时操作 按…...
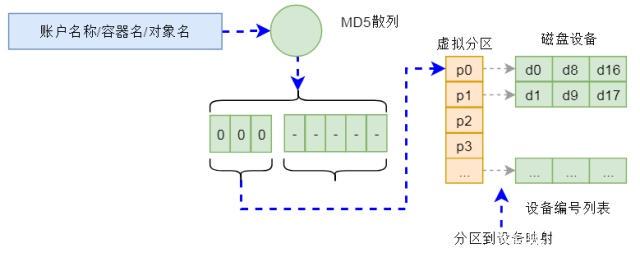
集中式存储和分布式存储
分布式存储是相对于集中式存储来说的,在介绍分布式存储之前,我们先看看什么是集中式存储。不久之前,企业级的存储设备都是集中式存储。所谓集中式存储,从概念上可以看出来是具有集中性的,也就是整个存储是集中在一个系…...
【机器学习数据集】如何获得机器学习的练习数据?
一、scikit-learn自带数据集Scikit-learn内置了很多可以用于机器学习的数据,可以用两行代码就可以使用这些数据。自带的小的数据集为:sklearn.datasets.load_<name>load_bostonBoston房屋价格回归506*13fetch_california_housing加州住房回归20640…...

【编程实践】使用 Kotlin HTTP 框架 Fuel 实现 GET,POST 接口 kittinunf.fuel【极简教程】
目录 Fuel 简介 实现代码 GET网络请求用法(有三种写法...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...