树与二叉树 总复习
一、树的定义
树是一个有n个(n>=0)结点的有限集合。
如果n=0,称为空树;
如果n>0,称为非空树,有且仅有一个特定的称为根Root的结点(无直接前驱)
如果n>1,除了根节点外,其他结点划分为m个互不相交的有限集合(记为T1、T2...TM),每个集合本身又是一棵树,称为根的子树(Sub-tree)。
每个结点肯定有唯一的前驱(除根节点外),但是可能有多个后继。
二、树的术语
结点:包含一个数据元素及若干指向其子树的分支
结点的度:结点拥有的子树个数,也即结点包含的分支个数
叶子结点(终端结点)
度为0的结点 {K,L,F,G,M,I,J}
分支结点()非终端结点
度不为0的结点 {A,B,C,D,E,H}
包含根结点
内部结点:除根之外的分支结点 {B,C,D,E,H}
孩子:结点的子树的根
双亲:孩子的直接前驱
兄弟:同一个双亲的其他孩子
子孙:以某结点为根的树中所有的结点
祖先:从该结点到根结点,经过所有分支结点
树的层次
根结点为第一层,根的孩子为第二层,依次类推。
深度:树中最大的层次
森林:互不相交的树的集合。对于树中每个结点而已,其子树的集合就是森林
二叉树 Binary Tree
每个结点最多只有两棵子树 最多两个孩子
二叉树的子树可以分成左右两个部分 称为左子树和右子树

二叉树的性质1
在二叉树的第i层上至多有2i-1个结点
深度为k的二叉树至多有2^k-1个结点
如果二叉树终端结点数为n0,度为2的结点数为n2,则no=n2+1
证明思路:总结点数n=no+n1+n2
考察分支数B:除了根之外,所有的结点都有且只有一个分支指向它不同度的结点产生不同个数的分支 n=B+1
不同度的结点产生不同个数的分支B=n1+2n2
no=n2+1
五、满二叉树
一个深度为k且有2^^k-1个结点的二叉树
每层上的结点数都是最大数 可以自上而下、自左至右连续编号
完全二叉树 当且仅当每一个结点都与深度相同的满二叉树中编号从1到n的结点一一一对应的二叉树
叶子结点只在最大两层上出现
以任何一个结点为根结点,其左子树深度与右子树深度相等或大于1
具有n个结点的完全二叉树 其深度为log2n取整+1
七、二叉树的存储结构:顺序存储
用一组连续的存储单元依次自上而下,自左至右存储结点
对于一般二叉树,空结点的位置也要按照完全二叉树编号
八、二叉树的链式存储结构
1、二叉链表
采用数据域加上左右孩子的指针
2、二叉链表的定义
二叉链表的一个结点的可以用一个结构体表示,里面包含的成员有一个数据域,两个指针域
struct BiNode binode: 双节点 node:节点
{
char data;
BiNode *Ichild,*rchild;
}
3、二叉树的链式存储结构
只能双亲找孩子,孩子难以找到双亲
4、二叉树的链式存储结构
三叉链表

遍历二茶树
根据访问根结点的次序
DLR
LDR
LRD
先序:
boid PreOrderTraverse(BinTree T)
{
if(T)
{
cout<<T->data;
PreOrderTraverse(T->IChild);
PreOrderTraverse()T->rChild):
先序中序、中序后序
都可以求出二叉树
而先序和后序不可以
因为不具备确定左右子树的能力。
树的存储结构
双亲表示法 找双亲容易找孩子难

孩子表示法:最大的缺点就是空指针链域太多 有些结点有很多孩子 有些结点的孩子很少:结构不均衡
n结点的树 度为d 多链表表示法中 空指针必有[(d-1)n+1]



树的路径:
路径:从树的一个结点到另一个结点之间的分支构成了两个结点之间的路径
路径长度:路径上的分支的数目
树的路径长度:从根结点到每个结点之间路径长度的和
如果结点权重不一样,我们可以计算带权路径长度
从结点到根结点之间的路径长度乘以该结点的权重
树的带权路径长度WPL Weighted path length
树中所有叶子结点的带权路径长度之和()度为0
相同的叶子结点数,叶子结点也具有相同的权重,但是不同的二叉树会产生不同的WOL
引出概念
树的带权路径长度WPL最小的二叉树被称为最优二叉树
Huffman 哈夫曼树
有什么special的place
权值最大的结点离根最近
权值最小的结点离根最远


有了编码
怎么解码
要能唯一解码对编码有什么要求
要求前缀编码
即任何一个字符编码都不是其他字符的前缀
Huffman是一种前缀编码
相关文章:

树与二叉树 总复习
一、树的定义 树是一个有n个(n>0)结点的有限集合。 如果n0,称为空树; 如果n>0,称为非空树,有且仅有一个特定的称为根Root的结点(无直接前驱) 如果n>1,除了根节点外&…...
window10安装MySQL数据库
准备好软件MySql的下载参考:(1137条消息) mysql下载与安装过程_weixin_40396510的博客-CSDN博客_mysql数据库下载安装(1137条消息) 安装MySQL的常见问题_二木成林的博客-CSDN博客_sc不是内部或外部命令,也不是可运行的程序解压要C盘(自定义,本…...
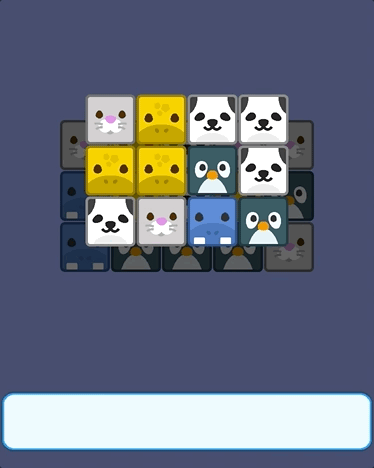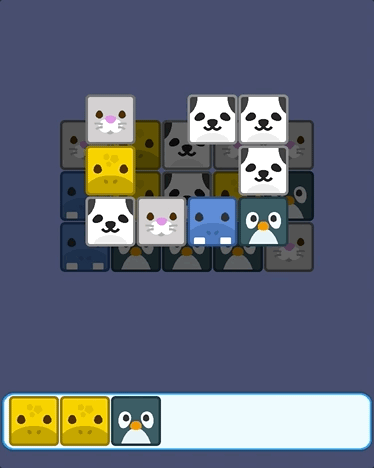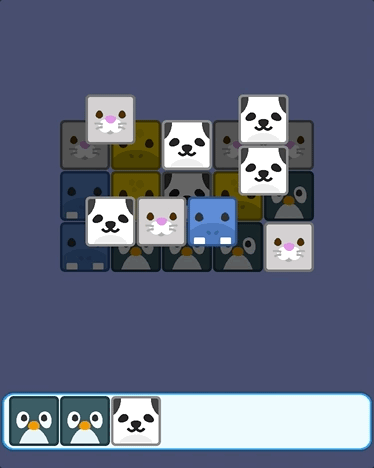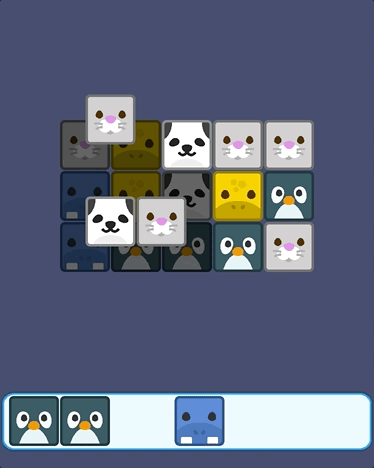
羊了个羊游戏开发教程3:卡牌拾取和消除
本文首发于微信公众号: 小蚂蚁教你做游戏。欢迎关注领取更多学习做游戏的原创教程资料,每天学点儿游戏开发知识。嗨!大家好,我是小蚂蚁。终于要写第三篇教程了,中间拖的时间有点儿长,以至于我的好几位学员等…...

SHA1详解
目录 一、介绍 二、与MD5的区别 1、对强行攻击的安全性 2、对密码分析的安全性 3、速度 三、应用 1、文件指纹 2、Git中标识对象 四、算法原理 1、填充消息 2、消息处理 3、数据运算 (1)链接变量 (2)步函数 一、介绍…...

Go并发介绍及其使用
1. goroutine Go语言通过go关键字来启动一个goroutine。注意:go关键字后面必须跟一个函数,不能是语句或者其他东西,函数的返回值被忽略。 goroutine有如下特性: go的执行是非阻塞的,不会等待。go后面的函数的返回值…...
小米手机屏幕解锁技巧精选
手机锁是一种保护存储的用户数据和信息的方法。存储在锁定手机中的所有信息比任何人都可以访问的手机安全得多。但有时,如果用户忘记了这些屏幕锁定,可能会造成麻烦。在此博客中,我们将帮助用户了解如何解锁小米手机。 什么时候需要解锁小米手…...

「SDOI2009」HH去散步
HH去散步 题目限制 内存限制:125.00MB时间限制:1.00s标准输入标准输出 题目知识点 动态规划 dpdpdp矩阵 矩阵乘法矩阵加速矩阵快速幂 思维 构造 题目来源 「SDOI2009」HH去散步 题目 题目背景 HH 有个一成不变的习惯,喜欢在饭后散步…...

用上Visual Studio后,我的世界游戏的构建时间减少了一半
今天我们讲述一个使用 Visual Studio 提升工作效率的案例。 我的世界(Minecraft) 游戏开发商 Mojang Studios 近日联系了 Visual Studio C 团队,因为他们需要将 C 开发扩展到新平台(Linux),同时还希望保留他们现有的技术基础&…...
34、基于51单片机锂电池电压电流容量检测仪表LCD液晶显示 原理图PCB程序设计
方案选择 单片机的选择 方案一:AT89C52是美国ATMEL公司生产的低电压,高性能CMOS型8位单片机,器件采用ATMEL公司的高密度、非易失性存储技术生产,兼容标准MCS-51指令系统,片内置通用8位中央处理器(CPU)和Flash存储单元…...
-基础使用)
【Java基础】泛型(一)-基础使用
本文以Java的官方文档为参考,辅以代码示例,尽可能详尽的叙述泛型的每一个特性 什么是泛型 泛型(Generics)也称为参数化类型(parameterized types),也就是将类型本身作为接口、类、方法中的参数…...

学Python不会不知道NumPy计算包吧,带你五分钟看懂NumPy计算包
从今天我们就开始进入 Python 数据分析工具的教程。 前段时间数据分析和Python都讲了一点点,但是Python的数据库,讲的少了点,所以接下来就讲讲这些重要的常用数据库吧!!! Python 数据分析绝对绕不过的四个…...
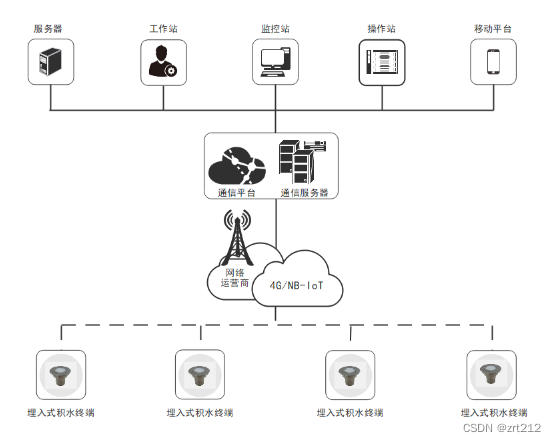
积水内涝监测——埋入式积水终端设备介绍
一、设备概述 埋入式积水终端是针对城市内涝推出的积水信息监测采集设备,采用超声波传感技术,对积水的深度进行精确的测量。产品能够在低温、腐蚀环境下可靠运行本产品特别适用于智慧城市中,对城市道路、社区低洼处的积水进行实时监测上报到…...
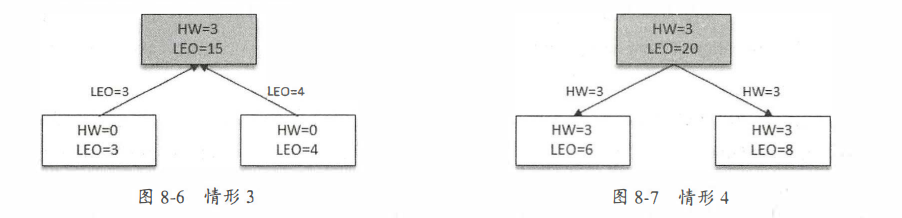
Kafka的日志同步
首先介绍下LEO和HW LEO: 即LogEndOffset,表示该副本下次日志记录的偏移量HW:即HighWatermark,高水位线,是所有ISR副本集合中的LEO最小值上图中,如果此时三个副本都在ISR集合中,那么此时他们的LE…...
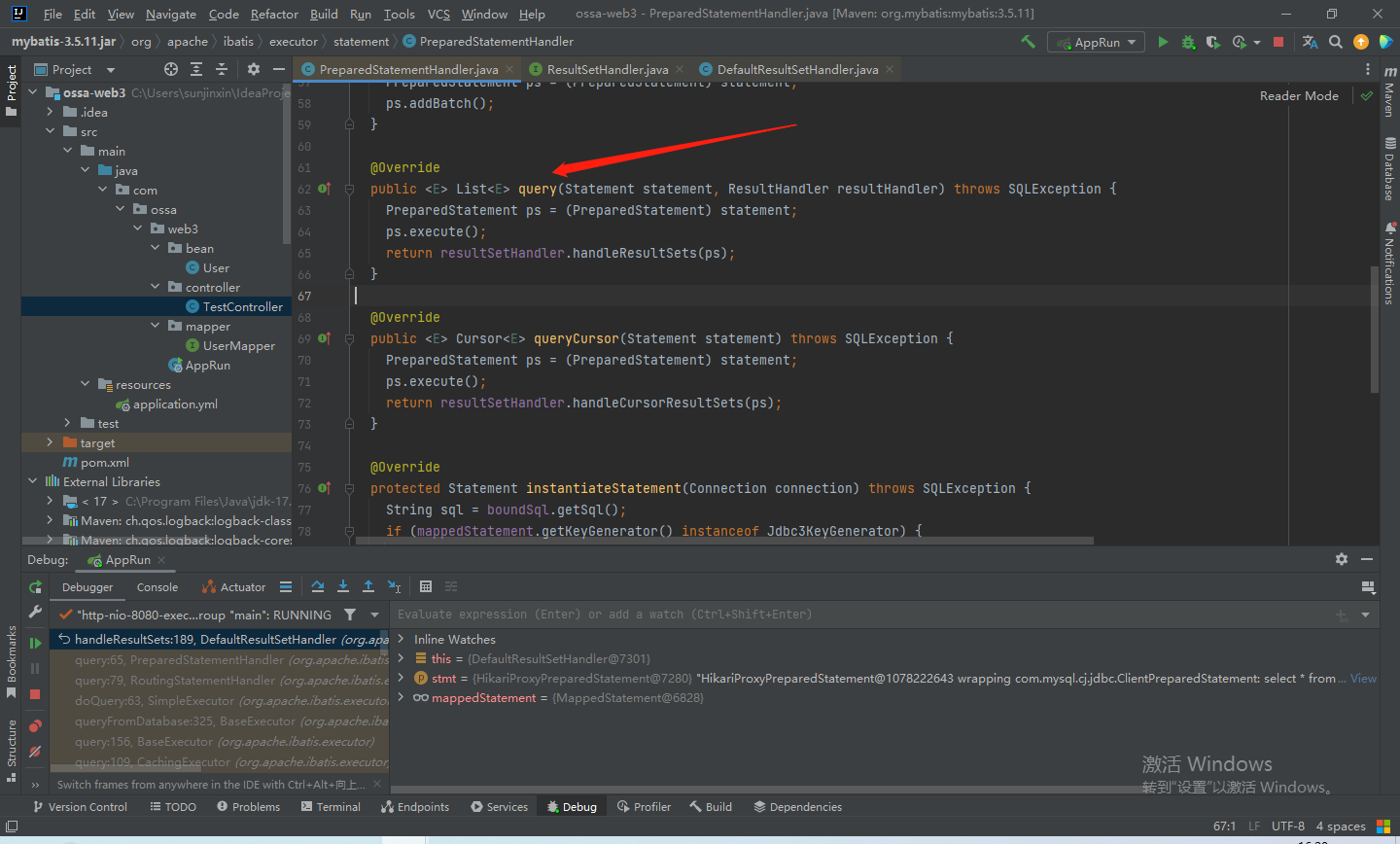
【Mybatis源码解析】mapper实例化及执行流程源码分析
文章目录简介环境搭建源码解析基础环境:JDK17、SpringBoot3.0、mysql5.7 储备知识:《【Spring6源码・AOP】AOP源码解析》、《JDBC详细全解》 简介 基于SpringBoot的Mybatis源码解析: 1.如何对mapper实例化bean 在加载BeanDefinition时&a…...
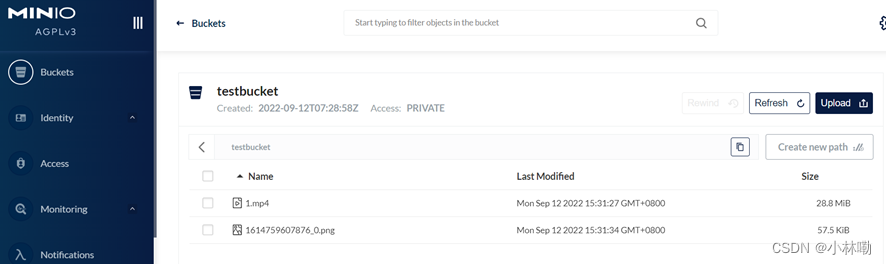
分布式文件管理系统(MinIO)
1.去中心化,每个点是对等的关系,通过Ngix对负载做均衡工作。 好处: 能够避免单点故障,将多块硬盘组成一个对象存储服务。 2. 使用纠删编码技术来保护数据,是一种回复丢失和损坏的数据的数学算法,他将数据分…...

Springcloud-配置中心config
一、添加依赖<dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-config-server</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId&…...

[项目篇] 音乐播放器开发报告
文章目录1. 项目描述:2. 项目上线展现:3. 项目具体实现:1. 登录2. 注册3.退出系统4.添加音乐4.1前后端交互约定4.2上传文件业务逻辑:4.3创建model包中的music类4.4在MusicMapper接口中,声明insertMusic抽象方法4.5在mybatis包中添…...
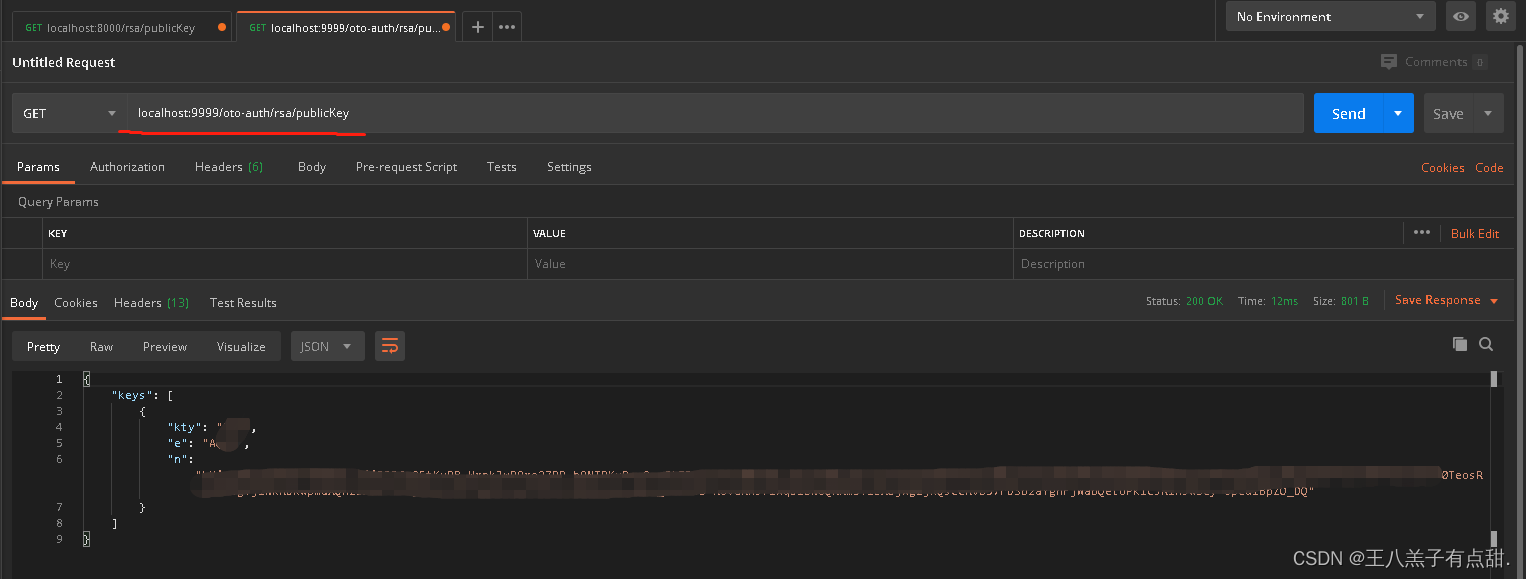
Spring Cloud Alibaba--gateway微服务详解之网关(二)
1、网关介绍 上篇对微服务中的nacos注册中心进行集成讲解。nacos主要作用是管理多服务之间复杂关系的组件。微服务是非常庞大且问题突出的架构,HTTP协议具有跨源资源共享 (CORS) Cross- Origin Resource Sharing机制,而处于安全考虑往往前端架构都会对跨…...
Zynq非VDMA方案实现视频3帧缓存输出,无需SDK配置,提供工程源码和技术支持
目录1、前言2、VDMA的不便之处3、FDMA取代VDMA实现视频缓存输出4、Vivado工程详解5、上板调试验证并演示6、福利:工程代码的获取1、前言 对于Zynq和Microblaze的用户而言,要想实现图像缓存输出,多半要使用Xilinx推荐的VDMA方案,该…...

血液透析过滤芯气密性检测装置中的高精度多段压力控制解决方案
摘要:针对目前血液过滤芯气密性检测过程中存在的自动化水平较低、多个检测压力之间需人工切换和压力控制精度较差的问题,为满足客户对高精度和自动化气密性检测的要求,本文提出了相应的解决方案。解决方案的主要特点是全过程的可编程压力控制…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
