KNN&K-means从入门到实战
作者:王同学 来源:投稿
编辑:学姐
1. 基本概念
1.1 KNN
k近邻法(k-nearest neighbor,k-NN)是一种基本分类与回归方法。
k近邻法的输入为实例的特征向量对应于特征空间的点;输出为实例的类别,可以取多类。
k近邻法假设给定一个训练数据集,其中的实例类别已定。分类时,对新的实例,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预测。因此,k近邻法不具有显式的学习过程。
k 近邻法1968年由Cover和Hart提出。
1.2 K-means
K-means是一种聚类方法,聚类是针对给定的样本,依据它们特征的相似度或距离,将其归并到若干个“类”或“簇”的数据分析问题。
聚类的目的是通过得到的类或簇来发现数据的特点或对数据进行处理。
聚类属于无监督学习,因为只是根据样本的相似度或距离将其进行归类,而类或簇事先并不知道。
1.3 KNN 和 K-means对比
KNN
-
分类算法
-
监督学习
-
数据集是带Label的数据
-
没有明显的训练过程,基于Memory-based learning
-
K值含义 - 对于一个样本X,要给它分类,首先从数据集中,在X附近找离它最近的K个数据点,将它划分为归属于类别最多的一类
K-means
-
聚类算法
-
非监督学习
-
数据集是无Label,杂乱无章的数据
-
有明显的训练过程
-
K值含义- K是事先设定的数字,将数据集分为K个簇,需要依靠人的先验知识
2. KNN原理、实现过程
2.1 KKN原理:
KNN算法最简单粗暴的就是将预测点与所有点距离进行计算,然后保存并排序,选出前面K个值看看哪些类别比较多,则预测的点属于哪类。
2 KNN过程:
对未知类别属性的数据集中的每个点依次执行以下操作:
(1) 计算已知类别数据集中的点与当前点之间的距离;
(2) 按照距离递增次序排序;
(3) 选取与当前点距离最小的k个点;
(4) 确定前k个点所在类别的出现频率;
(5) 返回前k个点出现频率最高的类别作为当前点的预测分类
2.2.1 距离度量(1)


2.2.2 K值选择(3)
2.2.2.1 K值选择过小:
-
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差(approximation error)会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。
-
但缺点是“学习”的估计误差(estimation error)会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。
-
换句话说,k 值的减小就意味着整体模型变得复杂,容易发生过拟合。
2.2.2.2 K值选择过大:
-
如果选择较大的k值,就相当于用较大邻域中的训练实例进行预测。
-
优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误。
-
换句话说,k值的增大就意味着整体的模型变得简单。
如果k=N,那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的。
2.2.2.3 那么该如何确定K取多少值好呢?
答案是通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
2.2.3 确定前k个点所在类别的出现频率(4)
eg.当K取4时候,包含3个红点和1个蓝点
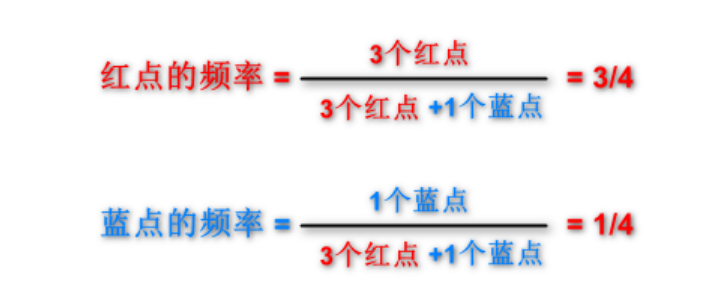
2.2.4 返回前k个点出现频率最高的类别作为当前点的预测分类(5)
因为3/4>1/4,所以预测的点的类别属于红色,KNN完成。
3.K-means原理、实现过程
3.1 K-means原理:
K-Means算法的特点是类别的个数是人为给定的,如果让机器自己去找类别的个数,通过一次次重复这样的选择质心计算距离后分类-再次选择新质心的流程,直到我们分组之后所有的数据都不会再变化了,也就得到了最终的聚合结果。
3.2K-means过程:
(1)随机选取k个质心(k值取决于你想聚成几类)
(2)计算样本到质心的距离,距离质心距离近的归为一类,分为k类
(3)求出分类后的每类的新质心
(4)再次计算计算样本到新质心的距离,距离质心距离近的归为一类
(5)判断新旧聚类是否相同,如果相同就代表已经聚类成功,如果没有就循环2-4步骤直到相同
3.2.1 随机选取k个质心(k值取决于你想聚成几类)
假设我想聚4类,那我们随机选取四个五角星作为质心(大哥)
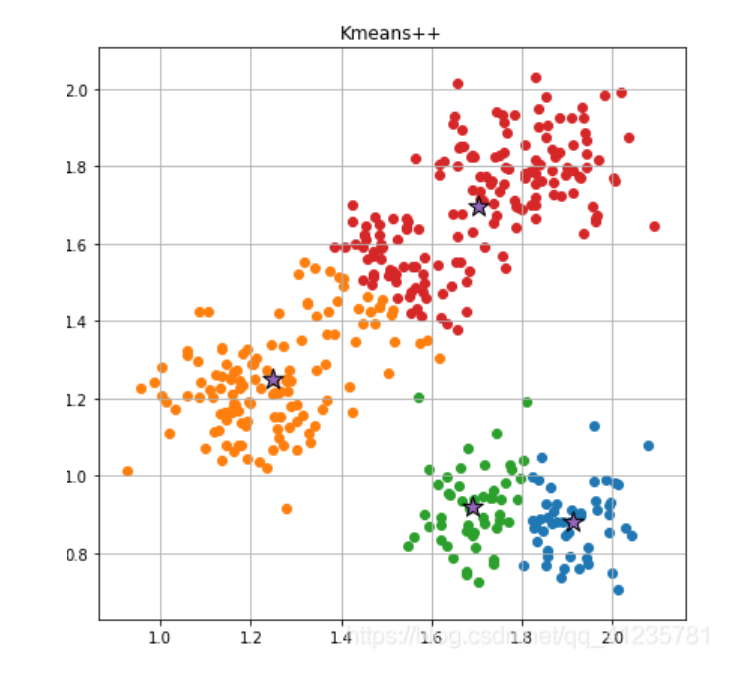
3.2.2 计算样本到质心的距离,距离质心距离近的归为一类,分为k类
计算除质心外的样本的欧式距离,样本离哪个质心近,该样本就跟哪个质心
换句话说就是,小圆点是小弟,五角星是大哥,小弟离哪个大哥近,那么这个小弟就跟哪个大哥混。
3.2.3 求出分类后的每类的新质心
上面我们已经分为4类了,这一步我们需要从4类中重新选出新的质心(新的大哥)。
3.2.4 再次计算计算样本到新质心的距离,距离质心距离近的归为一类
同样用上面方法计算样本到质心(新产生的大哥)的欧式距离,框起来的就是新大哥。
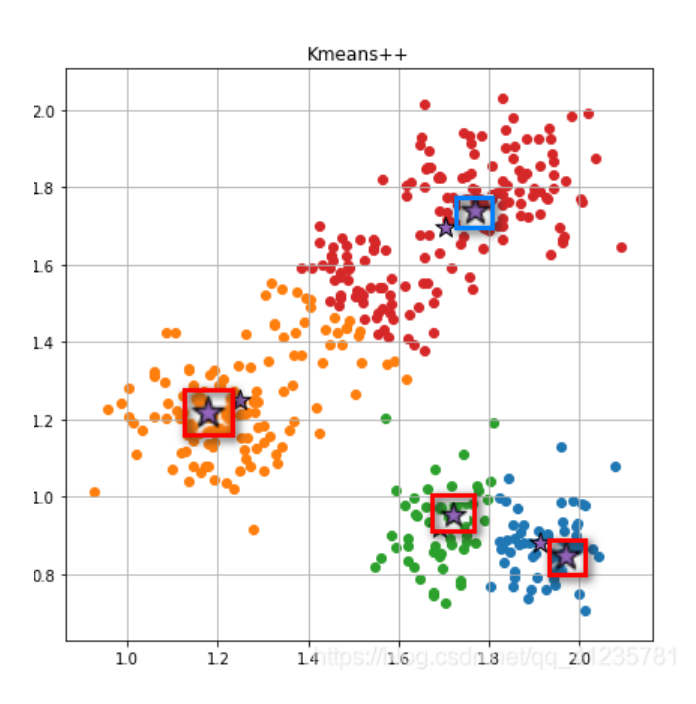
3.2.5 判断新旧聚类是否相同
当发现聚类情况并没有变化,这就说明我们的计算收敛已经结束了,不需要继续进行分组了,最终数据成功按照相似性分成了4组。即红、橙、绿、蓝,完成聚类。
4.总结:
4.1KNN
-
k 近邻法是基本且简单的分类与回归方法。k 近邻法的基本做法是∶ 对给定的训练实例点和输入实例点,首先确定输入实例点的k个最近邻训练实例点,然后利用这k个训练实例点的类的多数来预测输入实例点的类。
-
k 近邻模型对应于基于训练数据集对特征空间的一个划分。k 近邻法中,当训练集、距离度量、k值及分类决策规则确定后,其结果唯一确定。
-
k 近邻法三要素∶距离度量、k 值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的L。距离。k值小时,k 近邻模型更复杂;k值大时,k 近邻模型更简单。 k 值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的k。常用的分类决策规则是多数表决, 对应于经验风险最小化。
-
k 近邻法的实现需要考虑如何快速搜索k个最近邻点。kd树是一种便于对k 维空间中的数据进行快速检索的数据结构。kd树是二叉树,表示对k维空间的一个划分,其每个结点对应于k维空间划分中的一个超矩形区域。利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
4.2K-means
-
聚类是针对给定的样本,依据它们属性的相似度或距离,将其归并到若干个“类”或“簇”的数据分析问题。一个类是样本的一个子集。直观上,相似的样本聚集在同类,不相似的样本分散在不同类。
-
距离或相似度度量在聚类中起着重要作用。 常用的距离度量有闵可夫斯基距离,包括欧氏距离、曼哈顿距离、切比雪夫距离以及马哈拉诺比斯距离。常用的相似度度量有相关系数、夹角余弦。 用距离度量相似度时,距离越小表示样本越相似;用相关系数时,相关系数越大表示样本越相似。
-
k 均值聚类是常用的聚类算法,有以下特点。基于划分的聚类方法;类别数k 事先指定;以欧氏距离平方表示样本之间的距离或相似度,以中心或样本的均值表示类别;以样本和其所属类的中心之间的距离的总和为优化的目标函数;得到的类别是平坦的、非层次化的;算法是迭代算法,不能保证得到全局最优。
-
k均值聚类算法,首先选择k个类的中心,将样本分到与中心最近的类中,得到一个聚类结果;然后计算每个类的样本的均值,作为类的新的中心;重复以上步骤,直到收敛为止。
5.代码实战:
5.1 KNN实战:
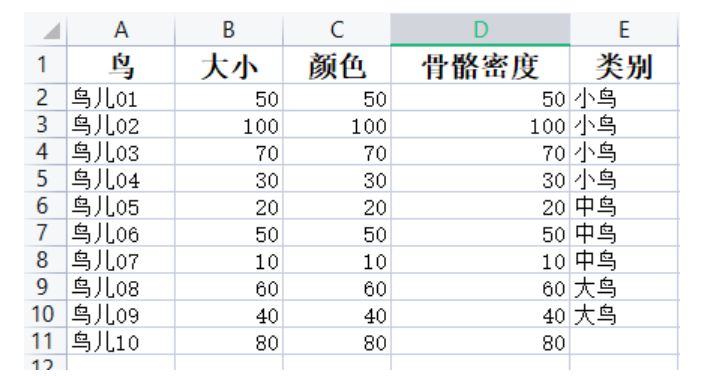
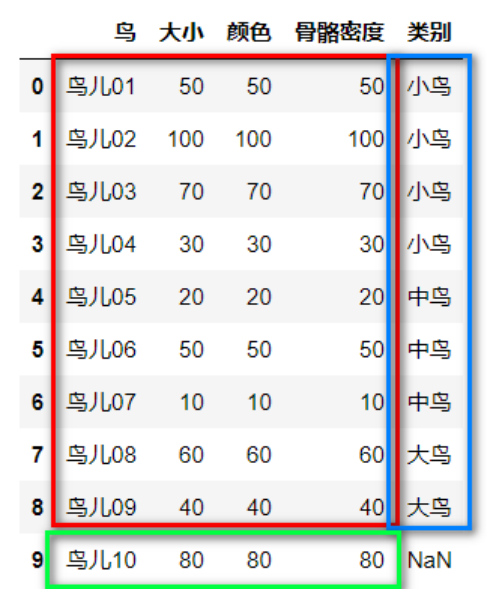
(1)首先自制一个数据集:
(2)导入工具包
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
(3)读取数据
data=pd.read_excel("knndata.xlsx")
data #打印出来看一下

(4)划分数据集
train_feature=data.iloc[0:9,1:4]#红色部分
train_label=data.iloc[0:9,4:5]#蓝色部分
test_feature=data.iloc[9:10,1:4]#绿色部分
(5)建模预测
knn=KNeighborsClassifier(n_neighbors=4)#n_neighbors=4即指定K值为4
knn.fit(train_feature,train_label)#模型训练
knn.predict(test_feature)#模型预测
输出:

5.2 K-means代码实战:
(1)自制个数据集
(2)导入工具包
import pandas as pd
from sklearn.cluster import KMeans
(3)读取数据
data=pd.read_excel("kmeans.xlsx")
data#打印看一下
(4)划分数据集
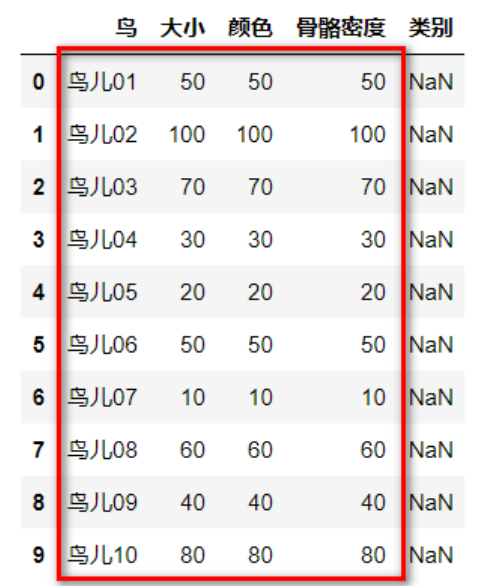
train_feature=data.iloc[0:10,1:4]#红色部分
(5)建模预测
kmeans = KMeans(n_clusters=3)#n_clusters=3即指定划分为3个类型
kmeans.fit(train_feature)#模型训练
label_kmeans = kmeans.predict(train_feature)#模型预测
label_kmeans
输出:
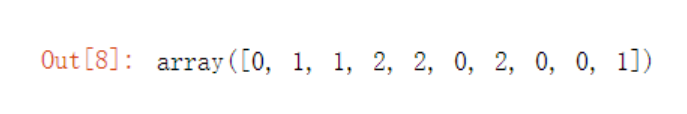
关注下方卡片《学姐带你玩AI》🚀🚀🚀
ACL&CVPR1000+篇论文等你来拿
回复“ACL”或“CVPR”免费领
码字不易,欢迎大家点赞评论收藏!
相关文章:
KNN&K-means从入门到实战
作者:王同学 来源:投稿 编辑:学姐 1. 基本概念 1.1 KNN k近邻法(k-nearest neighbor,k-NN)是一种基本分类与回归方法。 k近邻法的输入为实例的特征向量对应于特征空间的点;输出为实例的类别&…...
SpringBoot整合RabbitMQ
SpringBoot整合RabbitMQ,生产者 (1)创建maven项目 (2)引入依赖 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><versi…...
Hive---安装教程
Hive安装教程 Hive属于Hadoop生态圈,所以Hive必须运行在Hadoop上 文章目录Hive安装教程上传安装包解压并且更名修改 /etc/profile创建hive-site.xml将mysql的jar包放入Hive库中开启刷新配置文件hadoop开启mysql初始化启动hive上传安装包 将安装包上传到/opt/insta…...
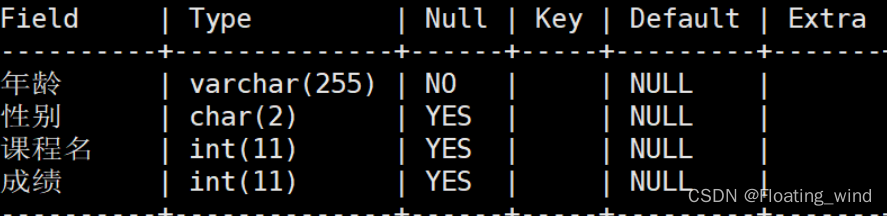
MySQL作业四
学生表:Student (Sno, Sname, Ssex , Sage, Sdept) 学号,姓名,性别,年龄,所在系 Sno为主键 课程表:Course (Cno, Cname,) 课程号,课程名 Cno为主键 学生选课表:SC (Sno, Cno, Score)…...
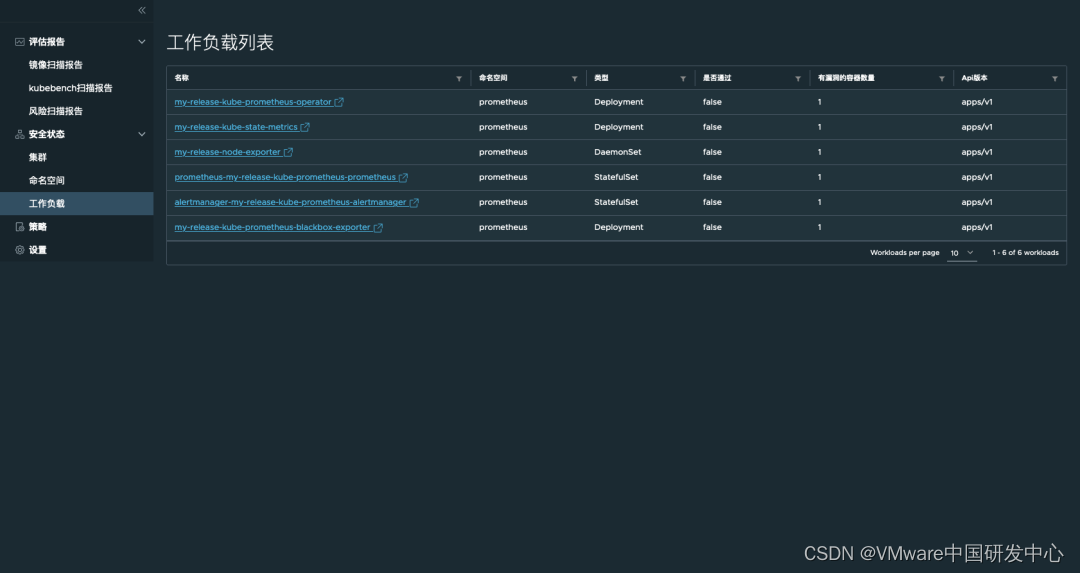
云原生安全检测器 Narrows(CNSI)的部署和使用
近日, 云原生安全检测器 Narrows(Cloud Native Security Inspector,简称CNSI)发布了0.2.0版本。 (https://github.com/vmware-tanzu/cloud-native-security-inspector) 此项目旨在对K8s集群中的工作负载进…...
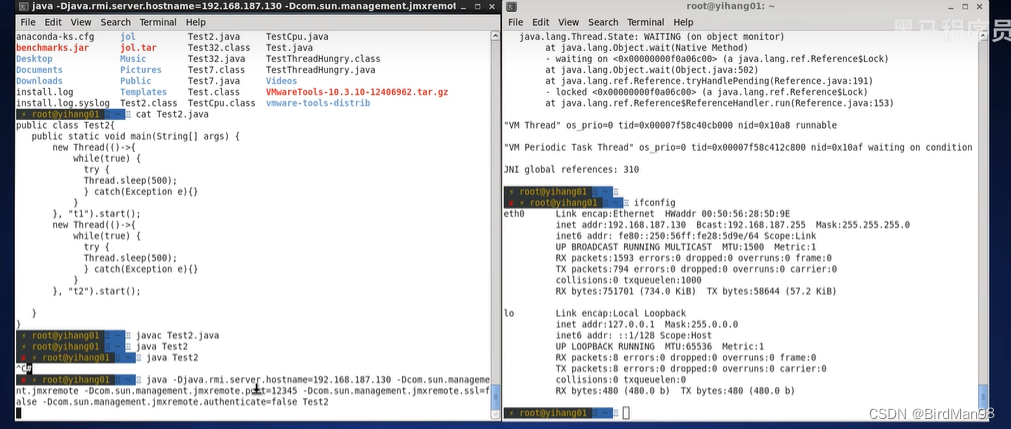
【并发编程】【3】Java线程 创建线程与线程运行
并发编程 3.Java线程 本章内容 创建和运行线程 查看线程 线程 API 线程状态 3.1 创建和运行线程 方法一,直接使用 Thread // 创建线程对象 Thread t new Thread() {public void run() {// 要执行的任务} }; // 启动线程 t.start();例如: // 构…...

Ambire 最新消息——2023 年 1 月
大家好,这里是我们在过去几周所做的一切的快速回顾。 发展 整个钱包的交易模拟和余额预测 我们推出了一项真正改变加密钱包 UX 游戏规则的功能:Ambire 现在向用户显示他们的钱包余额将如何更新,甚至在签署交易之前。 这项新功能可以分解为 Am…...

【kubeflow | 镜像源的解决方法——脚本】
20230214 方式一:获取所有镜像列表,自行外网拉取下载 获取KF所需镜像列表脚本 Offical docs for getting all kubeflow images curl https://gist.githubusercontent.com/Jason-CKY/7d7056ce261c6d606585f05218230037/raw/5c27297efdf6424cd9679b9f7…...
)
function calling convention(函数调用约定)
函数调用约定 函数调用约定,是指当一个函数被调用时,函数的参数会被传递给被调用的函数和返回值会被返回给调用函数。函数的调用约定就是描述参数是怎么传递和由谁平衡...

errgroup 原理简析
golang.org/x/sync/errgroup errgroup提供了一组并行任务中错误采集的方案。 先看注释 Package errgroup provides synchronization, error propagation, and Context cancelation for groups of goroutines working on subtasks of a common task. Group 结构体 // A Gro…...

Centos7.6 下 Docker 安装
Docker的自动化安装 官方的一键安装方式: curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun 国内 daocloud一键安装命令: curl -sSL https://get.daocloud.io/docker | sh Docker手动安装 手动安装Docker分三步:卸…...
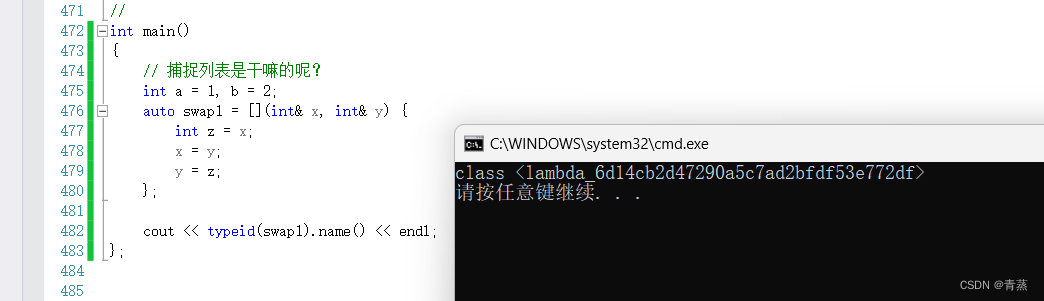
C++11--lambda表达式
目录 lambda表达式的概念 lambda表达式语法 lambda表达式的书写格式 捕捉列表 参数列表 mutable 返回值类型 函数体 lambda表达式交换两个数 函数对象与lambda表达式 lambda表达式的概念 lambda表达式是一个匿名函数 它能让代码更加地简洁 提高了代码可读性 首先定义…...
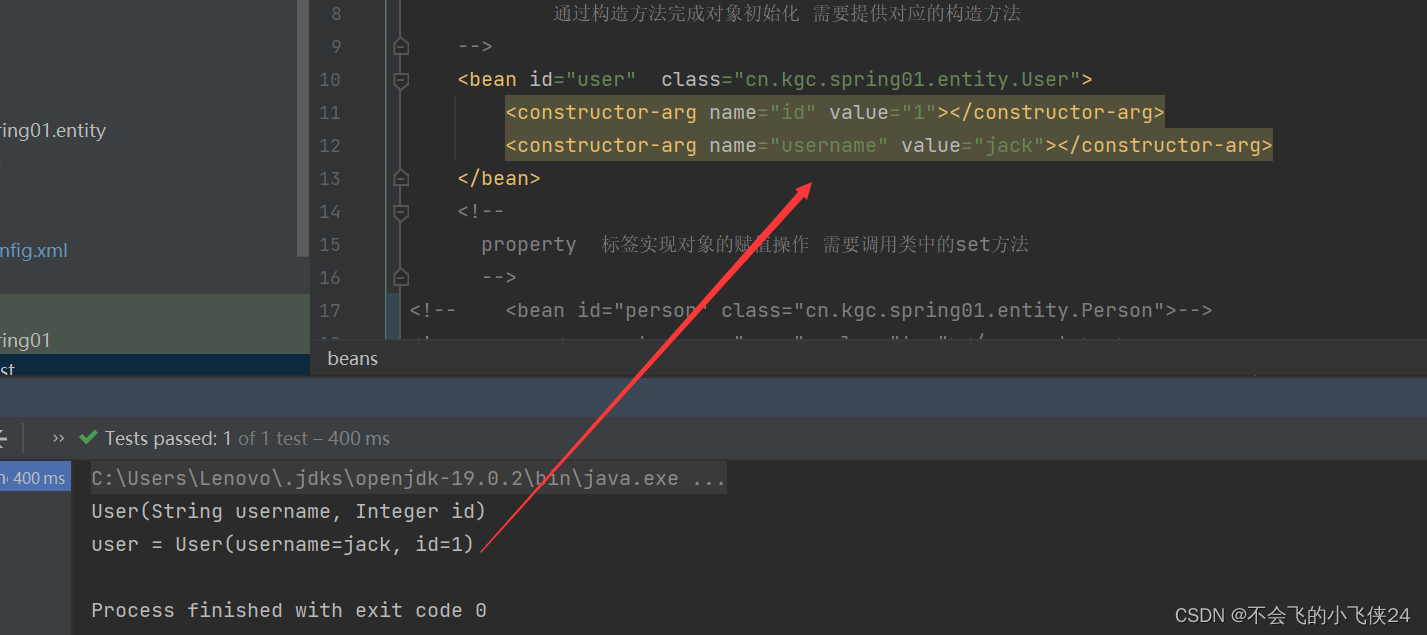
四【Spring框架】
目录一 Spring概述二 .Spring 的体系结构三 Spring的开发环境3.1 配置pom.xml文件四 项目案例:4.1 创建实体类4.2 在pom.xml中引入依赖4.3 配置Spring-config.xml文件4.4 Test✅作者简介:Java-小白后端开发者 🥭公认外号:球场上的…...

树与二叉树 总复习
一、树的定义 树是一个有n个(n>0)结点的有限集合。 如果n0,称为空树; 如果n>0,称为非空树,有且仅有一个特定的称为根Root的结点(无直接前驱) 如果n>1,除了根节点外&…...
window10安装MySQL数据库
准备好软件MySql的下载参考:(1137条消息) mysql下载与安装过程_weixin_40396510的博客-CSDN博客_mysql数据库下载安装(1137条消息) 安装MySQL的常见问题_二木成林的博客-CSDN博客_sc不是内部或外部命令,也不是可运行的程序解压要C盘(自定义,本…...
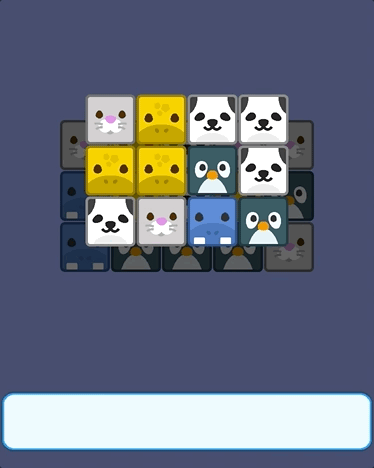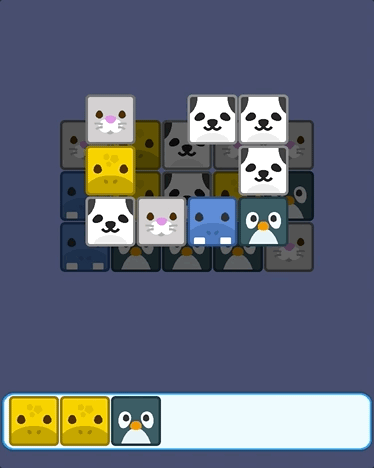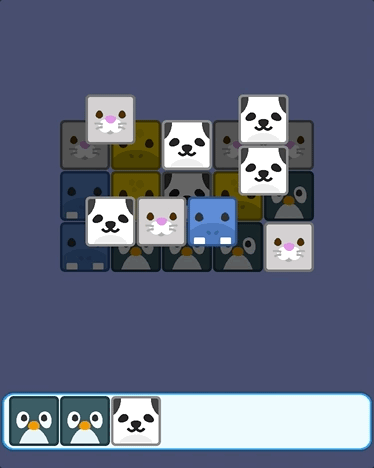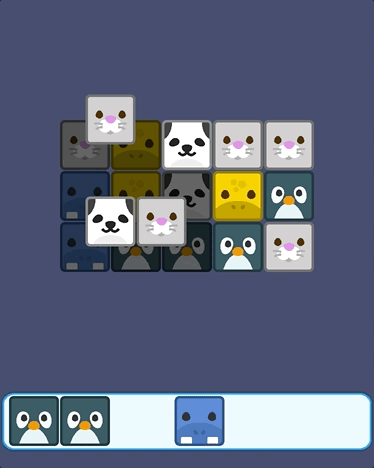
羊了个羊游戏开发教程3:卡牌拾取和消除
本文首发于微信公众号: 小蚂蚁教你做游戏。欢迎关注领取更多学习做游戏的原创教程资料,每天学点儿游戏开发知识。嗨!大家好,我是小蚂蚁。终于要写第三篇教程了,中间拖的时间有点儿长,以至于我的好几位学员等…...

SHA1详解
目录 一、介绍 二、与MD5的区别 1、对强行攻击的安全性 2、对密码分析的安全性 3、速度 三、应用 1、文件指纹 2、Git中标识对象 四、算法原理 1、填充消息 2、消息处理 3、数据运算 (1)链接变量 (2)步函数 一、介绍…...

Go并发介绍及其使用
1. goroutine Go语言通过go关键字来启动一个goroutine。注意:go关键字后面必须跟一个函数,不能是语句或者其他东西,函数的返回值被忽略。 goroutine有如下特性: go的执行是非阻塞的,不会等待。go后面的函数的返回值…...
小米手机屏幕解锁技巧精选
手机锁是一种保护存储的用户数据和信息的方法。存储在锁定手机中的所有信息比任何人都可以访问的手机安全得多。但有时,如果用户忘记了这些屏幕锁定,可能会造成麻烦。在此博客中,我们将帮助用户了解如何解锁小米手机。 什么时候需要解锁小米手…...

「SDOI2009」HH去散步
HH去散步 题目限制 内存限制:125.00MB时间限制:1.00s标准输入标准输出 题目知识点 动态规划 dpdpdp矩阵 矩阵乘法矩阵加速矩阵快速幂 思维 构造 题目来源 「SDOI2009」HH去散步 题目 题目背景 HH 有个一成不变的习惯,喜欢在饭后散步…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
