超螺旋滑模控制(STA)
超螺旋滑模控制(Super Twisting Algorithm, STA)
超螺旋滑模控制又称超扭滑模控制,可以说是二阶系统中最好用的滑模控制方法。
系统模型
对于二阶系统可以建立具有标准柯西形式的微分方程组
{x˙1=x2x˙2=f+g⋅u\begin{cases} \dot x_1 = x_2 \\ \dot x_2 = f + g \cdot u \end{cases} {x˙1=x2x˙2=f+g⋅u
与传统滑模相比,超螺旋滑模,使用积分来获取实际控制量,不含高频切换量,所以系统中没有抖振。
令滑模面为s,只要满足以下的方程,即为稳定
{s˙=−λ∣s∣12⋅sign(s)+νν˙=−α⋅sign(s)\begin{cases} \dot s = -\lambda |s| ^ {\frac {1} {2}} \cdot sign(s) + \nu \\ \dot \nu = - \alpha \cdot sign(s) \\ \end{cases} {s˙=−λ∣s∣21⋅sign(s)+νν˙=−α⋅sign(s)
控制器设计
设状态 x1x_1x1 的期望值为 xdx_dxd ,则跟踪误差为
{e1=x1−xde2=e˙1=x˙1−x˙d=x2−x˙d\begin{cases} e_1 = x_1 - x_d \\ e_2 = \dot e_1 = \dot x_1 - \dot x_d = x_2 - \dot x_d \end{cases} {e1=x1−xde2=e˙1=x˙1−x˙d=x2−x˙d
设计滑模面为
s=ce1+e2s = ce_1 + e_2 s=ce1+e2
则滑模面的导数为
s˙=ce˙1+e˙2=ce˙2+f+g⋅u−x¨d=−λ∣s∣12⋅sign(s)+ν=−λ∣s∣12⋅sign(s)−α⋅sign(s)\begin{align} \dot s & = c \dot e_1 + \dot e_2 \nonumber \\ & = c \dot e_2 + f + g \cdot u - \ddot x_d \nonumber\\ & = -\lambda |s| ^ {\frac {1} {2}} \cdot sign(s) + \nu \nonumber\\ & = -\lambda |s| ^ {\frac {1} {2}} \cdot sign(s) - \alpha \cdot sign(s) \nonumber\\ \end{align} s˙=ce˙1+e˙2=ce˙2+f+g⋅u−x¨d=−λ∣s∣21⋅sign(s)+ν=−λ∣s∣21⋅sign(s)−α⋅sign(s)
可以得到控制量
u=g−1(−f+x¨d−c1e2−λ∣s∣12sign(s)−α⋅sign(s))u = g ^ {-1} (-f + \ddot x_d - c_1e_2 - \lambda |s| ^ {\frac {1} {2}}sign(s) - \alpha \cdot sign(s)) u=g−1(−f+x¨d−c1e2−λ∣s∣21sign(s)−α⋅sign(s))
参数设定为
λ˙=ω1γ12α=λε+12(β+4ε2)\begin{align} \dot \lambda &= \omega _ 1 \sqrt{\frac {\gamma_1} {2}} \nonumber\\ \alpha &= \lambda \varepsilon + \frac{1}{2}(\beta+4\varepsilon ^ {2}) \nonumber \end{align} λ˙α=ω12γ1=λε+21(β+4ε2)
式中,α,β,ε,ω1,γ1\alpha , \beta , \varepsilon , \omega_1 , \gamma_1α,β,ε,ω1,γ1 均大于0。
稳定性证明
可以看出,控制量中含有的不再是滑模面,而是多项式 ∣s∣12|s| ^ {\frac {1} {2}}∣s∣21 。除此之外,在 s˙\dot ss˙ 中还出现了另一个参数 ν\nuν ,不妨把这两者定义为新的状态变量,在此基础上设成李雅普诺夫函数。
{z1=∣s∣12z2=ν⇒{z˙1=12∣s∣−12s˙=12∣s∣−12(−λ∣s∣12⋅sign(s)−α⋅sign(s))z˙2=ν˙=−α⋅sign(s)\begin{cases} z_1 = |s| ^ {\frac {1} {2}} \nonumber\\ z_2 = \nu \\ \end{cases} \Rightarrow \begin{cases} \dot z_1 = {\frac {1} {2}} |s| ^ {-\frac {1} {2}} \dot s = {\frac {1} {2}} |s| ^ {-\frac {1} {2}}(-\lambda |s| ^ {\frac {1} {2}} \cdot sign(s) - \alpha \cdot sign(s)) \\ \dot z_2 = \dot \nu = -\alpha \cdot sign(s) \\ \end{cases} {z1=∣s∣21z2=ν⇒{z˙1=21∣s∣−21s˙=21∣s∣−21(−λ∣s∣21⋅sign(s)−α⋅sign(s))z˙2=ν˙=−α⋅sign(s)
将第一项带入第二项
{z˙1=12∣z1∣(−λz1+z2)z˙2=ν˙=−α⋅sign(s)=−α⋅sign(s)∣s∣12∣s∣−12=−αz1∣z1∣⇒{z˙1=12∣z1∣(−λz1+z2)z˙2=−αz1∣z1∣\begin{align} &\begin{cases} \dot z_1 = \frac {1} {2|z_1|}(-\lambda z_1 + z_2) \\ \dot z_2 = \dot \nu = -\alpha \cdot sign(s) = -\alpha \cdot sign(s) |s| ^ {\frac {1}{2}} |s| ^ {-\frac {1}{2}} = -\alpha {\frac {z_1}{|z_1|}} \nonumber \end{cases} \\ \nonumber & \Rightarrow \\ \nonumber &\begin{cases} \dot z_1 = \frac {1} {2|z_1|}(-\lambda z_1 + z_2) \\ \dot z_2 = -\alpha {\frac {z_1}{|z_1|}} \\ \end{cases} \\ \end{align} \nonumber {z˙1=2∣z1∣1(−λz1+z2)z˙2=ν˙=−α⋅sign(s)=−α⋅sign(s)∣s∣21∣s∣−21=−α∣z1∣z1⇒{z˙1=2∣z1∣1(−λz1+z2)z˙2=−α∣z1∣z1
设置新的状态变量为
Z=[z1z2]Z = \begin{bmatrix} z_1 \\ z_2 \\ \end{bmatrix} Z=[z1z2]
设置李雅普诺夫函数为
V0=ZTPZ=(β+4ε2)z12+z22−4εz1z2V_0 = Z^TPZ = (\beta+4\varepsilon^2)z_1^2 + z_2^2 - 4\varepsilon z_1 z_2 V0=ZTPZ=(β+4ε2)z12+z22−4εz1z2
其中PPP 为
P=[β+4ε2−2ε−2ε1]P=\begin{bmatrix} \beta+4\varepsilon^2 & -2\varepsilon \\ -2\varepsilon & 1 \\ \end{bmatrix} P=[β+4ε2−2ε−2ε1]
李雅普诺夫函数的导数
对李雅普诺夫函数进行求导
V˙0=2(β+4ε2)z1z˙1+2z2z˙2−4εz˙1z2−4εz1z˙2=2(β+4ε2)z1(12∣z1∣(−λz1+z2))+2z2(−αz1∣z1∣)−4ε(12∣z1∣(−λz1+z2))z2−4εz1(−λz1+z2)=−1∣z1∣ZTQZ\begin{align} \dot V_0 &= 2(\beta+4\varepsilon^2)z_1 \dot z_1 + 2z_2 \dot z_2 - 4\varepsilon \dot z_1 z_2 - 4\varepsilon z_1 \dot z_2 \nonumber\\ &= 2(\beta+4\varepsilon^2)z_1 (\frac {1} {2|z_1|}(-\lambda z_1 + z_2)) + 2z_2(-\alpha {\frac {z_1}{|z_1|}}) - 4\varepsilon (\frac {1} {2|z_1|}(-\lambda z_1 + z_2)) z_2 - 4\varepsilon z_1 (-\lambda z_1 + z_2) \nonumber\\ &= - \frac {1} {|z_1|} Z^T Q Z \nonumber \end{align} V˙0=2(β+4ε2)z1z˙1+2z2z˙2−4εz˙1z2−4εz1z˙2=2(β+4ε2)z1(2∣z1∣1(−λz1+z2))+2z2(−α∣z1∣z1)−4ε(2∣z1∣1(−λz1+z2))z2−4εz1(−λz1+z2)=−∣z1∣1ZTQZ
其中 QQQ 为
Q=[−4αε+λ(β+4ε2)−12(β+4ε2)+α−λε−12(β+4ε2)+α−λε2ε]=[ABCD]Q = \begin{bmatrix} -4\alpha \varepsilon + \lambda(\beta+4 \varepsilon^2) & -\frac{1}{2}(\beta+4\varepsilon^2) + \alpha-\lambda \varepsilon \\ -\frac{1}{2} (\beta+4\varepsilon^2) + \alpha-\lambda \varepsilon & 2\varepsilon \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} Q=[−4αε+λ(β+4ε2)−21(β+4ε2)+α−λε−21(β+4ε2)+α−λε2ε]=[ACBD]
这样我们得到李雅普诺夫函数
V˙0=−1∣z1∣ZTQZ\dot V_0 = - \frac {1} {|z_1|} Z^T Q Z V˙0=−∣z1∣1ZTQZ
求 QQQ 的特征根
∣pI−Q∣=∣p−ABCp−D∣=p2−(A+D)p+AD−BC=0|pI -Q| = \begin{vmatrix} p-A & B \\ C & p - D \end{vmatrix} = p^2-(A+D)p + AD - BC = 0 ∣pI−Q∣=p−ACBp−D=p2−(A+D)p+AD−BC=0
解方程组解得特征根为
{pmax(Q)=A+D+(A−D)2+4BC2pmin(Q)=A+D−(A−D)2+4BC2\begin{cases} p_{max}(Q) = \frac {A+D + \sqrt{(A-D)^2+4BC}} {2}\\ p_{min}(Q) = \frac {A+D - \sqrt{(A-D)^2+4BC}} {2} \end{cases} ⎩⎨⎧pmax(Q)=2A+D+(A−D)2+4BCpmin(Q)=2A+D−(A−D)2+4BC
所以
pmin(Q)ZTZ=A+D+(A−D)2+4BC2(z12+z22)p_{min}(Q) Z^T Z = \frac {A+D + \sqrt{(A-D)^2+4BC}} {2} (z_1^2 + z_2^2) pmin(Q)ZTZ=2A+D+(A−D)2+4BC(z12+z22)
ZTQZ=Az12+(B+C)Z1Z2+Dz22Z^TQZ = A z_1^2 + (B+C)Z_1Z_2 + Dz_2^2 ZTQZ=Az12+(B+C)Z1Z2+Dz22
比较 $p_{min}(Q) Z^T Z 与与与Z^TQZ$的大小,为了简便运算,将根号项用 RRR 表示
Dval=2(ZTQZ−pmin(Q)ZTZ)=(A−D+R)z12+(D−A+R)z22+2(B+C)z1z2=(A−D+R)[z12+(D−A+R)(A−D+R)z22+2(B+C)(A−D+R)z1z2]=(A−D+R)[z12+(D−A+R)(D+R−A)(A−D+R)(D+R−A)z22+2(B+C)(R+D−A)(A−D+R)(R+D−A)z1z2]=(A−D+R)[z12+(D+R−A)24BCz22+2(B+C)(R+D−A)4BCz1z2]=(A−D+R)[z12+(D+R−A)24BCz22+(D+R−A)24BCz1z2(D+R−A)24BCz1z2+2(B+C)(R+D−A)4BCz1z2]=(A−D+R)[(z1+D+R−A2BCz2)2+(2B+2C−4BC)(R+D−A)4BCz1z2]\begin{align} D_{val} &=2(Z^TQZ - p_{min}(Q) Z^T Z ) \nonumber\\ &= (A-D+R)z_1^2+(D-A+R)z_2^2+2(B+C)z_1z_2 \nonumber\\ &= (A-D+R)\left[z_1^2 + \frac{(D-A+R)}{(A-D+R)}z_2^2 + \frac{2(B+C)}{(A-D+R)}z_1z_2\right] \nonumber\\ &= (A-D+R)\left[z_1^2 + \frac{(D-A+R)(D+R-A)}{(A-D+R)(D+R-A)}z_2^2 + \frac{2(B+C)(R+D-A)}{(A-D+R)(R+D-A)}z_1z_2\right] \nonumber \\ &= (A-D+R)\left[z_1^2 + \frac{(D+R-A)^2}{4BC}z_2^2 + \frac{2(B+C)(R+D-A)}{4BC}z_1z_2\right] \nonumber\\ &= (A-D+R)\left[z_1^2 + \frac{(D+R-A)^2}{4BC}z_2^2 + \sqrt{\frac{(D+R-A)^2}{4BC}}z_1z_2 \sqrt{\frac{(D+R-A)^2}{4BC}}z_1z_2 + \frac{2(B+C)(R+D-A)}{4BC}z_1z_2\right] \nonumber\\ &= (A-D+R)\left[(z_1 + \frac{D+R-A}{2 \sqrt{BC}}z_2)^2 + \frac{(2B+2C-4\sqrt{BC})(R+D-A)}{4BC}z_1z_2\right] \nonumber\\ \end{align} Dval=2(ZTQZ−pmin(Q)ZTZ)=(A−D+R)z12+(D−A+R)z22+2(B+C)z1z2=(A−D+R)[z12+(A−D+R)(D−A+R)z22+(A−D+R)2(B+C)z1z2]=(A−D+R)[z12+(A−D+R)(D+R−A)(D−A+R)(D+R−A)z22+(A−D+R)(R+D−A)2(B+C)(R+D−A)z1z2]=(A−D+R)[z12+4BC(D+R−A)2z22+4BC2(B+C)(R+D−A)z1z2]=(A−D+R)[z12+4BC(D+R−A)2z22+4BC(D+R−A)2z1z24BC(D+R−A)2z1z2+4BC2(B+C)(R+D−A)z1z2]=(A−D+R)[(z1+2BCD+R−Az2)2+4BC(2B+2C−4BC)(R+D−A)z1z2]
上式中
R+A−D=(A−D)2+4BC+(A−D)≥0R + A - D = \sqrt{(A-D)^2+4BC} + (A - D) \ge 0 R+A−D=(A−D)2+4BC+(A−D)≥0
(z1+D+R−A2BCz2)2≥0(z_1 + \frac{D+R-A}{2 \sqrt{BC}}z_2)^2 \ge 0 (z1+2BCD+R−Az2)2≥0
{2B+2C−4BC≥0R+D−A=(A−D)2+4BC+(D−A)≥0⇒(2B+2C−4BC)(R+D−A)4BC≥0\begin{cases} 2B+2C-4\sqrt{BC} \ge 0 \\ R+D-A = \sqrt{(A-D)^2+4BC} + (D - A) \ge 0 \\ \end{cases} \Rightarrow \frac{(2B+2C-4\sqrt{BC})(R+D-A)}{4BC} \ge 0 {2B+2C−4BC≥0R+D−A=(A−D)2+4BC+(D−A)≥0⇒4BC(2B+2C−4BC)(R+D−A)≥0
所以我们得到
ZTQZ≥pmin(Q)ZTZZ^TQZ \ge p_{min}(Q) Z^T Z ZTQZ≥pmin(Q)ZTZ
同理可证
ZTQZ≤pmax(Q)ZTZZ^TQZ \le p_{max}(Q) Z^T Z ZTQZ≤pmax(Q)ZTZ
李雅普诺夫函数导数的变换
上式是根据 V˙0=−1∣z1∣ZTQZ\dot V_0 = -\frac {1} {|z_1|} Z^TQZV˙0=−∣z1∣1ZTQZ 做出的,对于 V0=ZTPZV_0 = Z ^ T P ZV0=ZTPZ 同样根据上式可得
向量的0范数,向量中非零元素的个数
向量的1范数,向量中各元素绝对值的模
向量的2范数,通常意义上的模值,欧几里得范数
向量的无穷范数,向量的最大值矩阵的1范数,列和范数,所有矩阵列向量绝对值之和的最大值
矩阵的2范数,谱范数,即 ATAA^TAATA矩阵的最大特征值的开平方
矩阵的无穷范数,行和范数,所有矩阵行向量绝对值之和的最大值
矩阵的F范数,Forbenius范数,所有矩阵元素绝对值的平方和再开放
ZTPZ≥pmin(P)ZTZ⇒(ZTPZ)1/2≥pmin1/2(P)(ZTZ)1/2=pmin1/2(P)∥Z∥⇒∥Z∥≤(ZTPZ)1/2pmin1/2(P)=V01/2pmin1/2(P)\begin{gather} Z^TPZ \ge p_{min}(P)Z^TZ \nonumber\\ \Rightarrow (Z^TPZ)^{1/2} \ge p_{min}^{1/2}(P)(Z^TZ)^{1/2} = p_{min}^{1/2}(P) \Vert Z \Vert \nonumber\\ \Rightarrow \Vert Z\Vert \le \frac{(Z^TPZ)^{1/2}}{p_{min}^{1/2}(P)} = \frac {V_0^{1/2}} {p_{min}^{1/2}(P)} \nonumber \end{gather} ZTPZ≥pmin(P)ZTZ⇒(ZTPZ)1/2≥pmin1/2(P)(ZTZ)1/2=pmin1/2(P)∥Z∥⇒∥Z∥≤pmin1/2(P)(ZTPZ)1/2=pmin1/2(P)V01/2
ZZZ的欧几里得范数为
∥Z∥=z12+z22=(∣s∣12sign(s))2+ν2=∣s∣+ν≥∣s∣=∣z1∣\Vert Z \Vert = \sqrt {z_1^2 + z_2^2} = \sqrt{(|s| ^ {\frac {1} {2}}sign(s) )^2 + \nu ^ 2} = \sqrt{|s| + \nu} \ge \sqrt{|s|} = |z_1| ∥Z∥=z12+z22=(∣s∣21sign(s))2+ν2=∣s∣+ν≥∣s∣=∣z1∣
所以
−1∣z1∣≤−1∥Z∥-\frac {1}{\vert z_1 \vert} \le -\frac {1}{\Vert Z \Vert} −∣z1∣1≤−∥Z∥1
我们再次回到 V˙0\dot V_0V˙0
V˙0=−1∣z1∣ZTQZ≤−1∣z1∣pmin(Q)ZTZ=−1∣z1∣pmin(Q)∥Z∥2≤−1∥Z∥pmin(Q)∥Z∥2=−pmin(Q)∥Z∥≤−pmin(Q)V012pmin12(P)=−rV012\begin{align} \dot V_0 &= - \frac{1} {|z_1|} Z^TQZ \le - \frac{1} {|z_1|} p_{min}(Q)Z^TZ \nonumber \\ &= - \frac{1} {|z_1|} p_{min}(Q) \Vert Z \Vert ^ 2 \le -\frac {1}{\Vert Z \Vert} p_{min}(Q) \Vert Z \Vert ^ 2 \nonumber\\ &= -p_{min}(Q) \Vert Z \Vert \le -p_{min}(Q) \frac {V_0^{\frac{1}{2}}} {p_{min}^{\frac{1}{2}}(P)} \nonumber\\ &= -r V_0^{\frac{1}{2}} \nonumber \end{align} V˙0=−∣z1∣1ZTQZ≤−∣z1∣1pmin(Q)ZTZ=−∣z1∣1pmin(Q)∥Z∥2≤−∥Z∥1pmin(Q)∥Z∥2=−pmin(Q)∥Z∥≤−pmin(Q)pmin21(P)V021=−rV021
其中
r=pmin(Q)pmin1/2(P)r = \frac {p_{min}(Q)} {p_{min}^{1/2}(P)} r=pmin1/2(P)pmin(Q)
若系统满足 V˙≤−rV12\dot V \le -rV^{\frac {1} {2}}V˙≤−rV21 其中r>0r>0r>0 ,则系统可以在有限时间内稳定
矩阵Q正定性的保证
上面的证明保证了系统具有李雅普诺夫稳定性,但是只有在r>0r > 0r>0的情况下才能保证系统稳定,此时需要 pmin(Q){p_{min}(Q)}pmin(Q)
与 pmin1/2(P){p_{min}^{1/2}(P)}pmin1/2(P) 保持同号,由于矩阵PPP为正定矩阵,所以pmin1/2(P){p_{min}^{1/2}(P)}pmin1/2(P)必大于0,那么需要保证pmin(Q){p_{min}(Q)}pmin(Q)也大于0。
正定矩阵的特征值都是正数
Q=[−4αε+λ(β+4ε2)−12(β+4ε2)+α−λε−12(β+4ε2)+α−λε2ε]Q = \begin{bmatrix} -4\alpha \varepsilon + \lambda(\beta+4 \varepsilon^2) & -\frac{1}{2}(\beta+4\varepsilon^2) + \alpha-\lambda \varepsilon \\ -\frac{1}{2} (\beta+4\varepsilon^2) + \alpha-\lambda \varepsilon & 2\varepsilon \end{bmatrix} Q=[−4αε+λ(β+4ε2)−21(β+4ε2)+α−λε−21(β+4ε2)+α−λε2ε]
不妨直接取
α=λε+12(β+4ε2)\alpha = \lambda \varepsilon + \frac{1}{2}(\beta+4\varepsilon^2) α=λε+21(β+4ε2)
这样的话可以简化一下
Q=[(λ−2ε)(β+4ε2)−4λε2002ε]Q = \begin{bmatrix} (\lambda-2\varepsilon)(\beta+4 \varepsilon^2)-4\lambda \varepsilon^2 & 0\\ 0 & 2\varepsilon \end{bmatrix} Q=[(λ−2ε)(β+4ε2)−4λε2002ε]
所以 QQQ 的特征根为
{p1=(λ−2ε)(β+4ε2)−4λε2p2=2ε\begin{cases} p_1 = (\lambda-2\varepsilon)(\beta+4 \varepsilon^2)-4\lambda \varepsilon^2 \\ p_2 = 2\varepsilon \end{cases} {p1=(λ−2ε)(β+4ε2)−4λε2p2=2ε
由于 ε>0\varepsilon > 0ε>0 所以 p2>0p_2 > 0p2>0非常显然,现在只需要保证 p1>0p_1>0p1>0,则可以有
λ>2ε(β+4ε2)β\lambda > \frac{2\varepsilon(\beta+4\varepsilon^2)} {\beta} λ>β2ε(β+4ε2)
重写李雅普诺夫函数
上一节中给出了保证 QQQ 正定性的条件,但是 α\alphaα 和 λ\lambdaλ 这两个参数值是人为给出的,因此需要把这两个参数加入到李雅普诺夫函数中来
V=V0+12γ1(λ−λ∗)2+12γ2(α−α∗)2V = V_0 + \frac {1} {2\gamma_1} (\lambda-\lambda^{*})^2 + \frac{1}{2\gamma_2} (\alpha-\alpha^{*})^2 V=V0+2γ11(λ−λ∗)2+2γ21(α−α∗)2
其中 λ∗α∗\lambda^{*} \ \alpha^{*}λ∗ α∗ 为未知常数,对其求导
V˙=V˙0+1γ1(λ−λ∗)λ˙+1γ2(α−α∗)α˙≤−rV012+1γ1(λ−λ∗)λ˙+1γ2(α−α∗)α˙=−rV012+1γ1(λ−λ∗)λ˙+1γ2(α−α∗)α˙−ω12γ1∣λ−λ∗∣+ω12γ1∣λ−λ∗∣−ω22γ2∣α−α∗∣+ω22γ2∣α−α∗∣\begin{align} \dot V &= \dot V_0 + \frac {1} {\gamma_1} (\lambda-\lambda^{*})\dot \lambda + \frac{1}{\gamma_2} (\alpha-\alpha^{*})\dot \alpha \le -r V_0^{\frac{1}{2}} + \frac {1} {\gamma_1} (\lambda-\lambda^{*})\dot \lambda + \frac{1}{\gamma_2} (\alpha-\alpha^{*})\dot \alpha \nonumber\\ &= -r V_0^{\frac{1}{2}} + \frac {1} {\gamma_1} (\lambda-\lambda^{*})\dot \lambda + \frac{1}{\gamma_2} (\alpha-\alpha^{*})\dot \alpha -\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}|+\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}| -\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}|+\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}| \nonumber \end{align} V˙=V˙0+γ11(λ−λ∗)λ˙+γ21(α−α∗)α˙≤−rV021+γ11(λ−λ∗)λ˙+γ21(α−α∗)α˙=−rV021+γ11(λ−λ∗)λ˙+γ21(α−α∗)α˙−2γ1ω1∣λ−λ∗∣+2γ1ω1∣λ−λ∗∣−2γ2ω2∣α−α∗∣+2γ2ω2∣α−α∗∣
根据 (x2+y2+z2)≤∣x∣+∣y∣+∣z∣(x^2 + y^2 + z^2) \le |x| + |y| + |z|(x2+y2+z2)≤∣x∣+∣y∣+∣z∣ 有
−rV012−ω12γ1∣λ−λ∗∣−ω22γ2∣α−α∗∣≤−[r2V012+ω122γ1∣λ−λ∗∣2+ω222γ2∣α−α∗∣2]12-r V_0^{\frac{1}{2}} - \frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}|-\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}| \le - \left[r^2V_0^{\frac{1}{2}}+ \frac {\omega_1^2} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}|^2 + \frac {\omega_2^2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}|^2\right]^{\frac{1}{2}} −rV021−2γ1ω1∣λ−λ∗∣−2γ2ω2∣α−α∗∣≤−[r2V021+2γ1ω12∣λ−λ∗∣2+2γ2ω22∣α−α∗∣2]21
设 r,ω1,ω2r,\omega_1,\omega_2r,ω1,ω2 中最小的数为 nnn,则上式为
[r2V012+ω122γ1∣λ−λ∗∣2+ω222γ2∣α−α∗∣2]12≤−n[V012+12γ1∣λ−λ∗∣2+12γ2∣α−α∗∣2]=−nV12\left[r^2V_0^{\frac{1}{2}}+ \frac {\omega_1^2} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}|^2 + \frac {\omega_2^2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}|^2\right]^{\frac{1}{2}} \le-n \left[V_0^{\frac{1}{2}}+ \frac {1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}|^2 + \frac {1} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}|^2 \right] = -nV^{\frac{1}{2}} [r2V021+2γ1ω12∣λ−λ∗∣2+2γ2ω22∣α−α∗∣2]21≤−n[V021+2γ11∣λ−λ∗∣2+2γ21∣α−α∗∣2]=−nV21
带入 V˙\dot VV˙ 有
V˙≤−rV012+1γ1(λ−λ∗)λ˙+1γ2(α−α∗)α˙−ω12γ1∣λ−λ∗∣+ω12γ1∣λ−λ∗∣−ω22γ2∣α−α∗∣+ω22γ2∣α−α∗∣≤−nV12+1γ1(λ−λ∗)λ˙+1γ2(α−α∗)α˙+ω12γ1∣λ−λ∗∣+ω22γ2∣α−α∗∣\begin {align} \dot V &\le -r V_0^{\frac{1}{2}} + \frac {1} {\gamma_1} (\lambda-\lambda^{*})\dot \lambda + \frac{1}{\gamma_2} (\alpha-\alpha^{*})\dot \alpha -\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}|+\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}| -\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}|+\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}| \nonumber\\ &\le -nV^{\frac{1}{2}} + \frac {1} {\gamma_1} (\lambda-\lambda^{*})\dot \lambda + \frac{1}{\gamma_2} (\alpha-\alpha^{*})\dot \alpha +\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}| +\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}| \nonumber \end {align} V˙≤−rV021+γ11(λ−λ∗)λ˙+γ21(α−α∗)α˙−2γ1ω1∣λ−λ∗∣+2γ1ω1∣λ−λ∗∣−2γ2ω2∣α−α∗∣+2γ2ω2∣α−α∗∣≤−nV21+γ11(λ−λ∗)λ˙+γ21(α−α∗)α˙+2γ1ω1∣λ−λ∗∣+2γ2ω2∣α−α∗∣
由于 λ∗α∗\lambda^{*} \ \alpha^{*}λ∗ α∗ 为未知常数,那我们假设 λ∗>λ,α∗>α\lambda^{*}>\lambda , \alpha^{*} > \alphaλ∗>λ,α∗>α ,总能找到两个常数满足这两个条件
V˙≤−nV12+1γ1(λ−λ∗)λ˙+1γ2(α−α∗)α˙+ω12γ1∣λ−λ∗∣+ω22γ2∣α−α∗∣=−nV12−1γ1∣λ−λ∗∣λ˙−1γ2∣α−α∗∣α˙+ω12γ1∣λ−λ∗∣+ω22γ2∣α−α∗∣=−nV12+∣λ−λ∗∣(ω12γ1−λ˙γ1)+∣α−α∗∣(ω22γ2−λ˙γ2)\begin{align} \dot V &\le -nV^{\frac{1}{2}} + \frac {1} {\gamma_1} (\lambda-\lambda^{*})\dot \lambda + \frac{1}{\gamma_2} (\alpha-\alpha^{*})\dot \alpha +\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}| +\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}| \nonumber\\ &= -nV^{\frac{1}{2}} - \frac {1} {\gamma_1} |\lambda-\lambda^{*}|\dot \lambda - \frac{1}{\gamma_2} |\alpha-\alpha^{*}|\dot \alpha +\frac {\omega_1} {\sqrt{2 \gamma_1}} |\lambda - \lambda^{*}| +\frac {\omega_2} {\sqrt{2 \gamma_2}} |\alpha - \alpha^{*}| \nonumber\\ &= -nV^{\frac{1}{2}} + |\lambda-\lambda^{*}|(\frac {\omega_1} {\sqrt{2 \gamma_1}} - \frac{\dot \lambda} {\gamma_1}) + |\alpha-\alpha^{*}|(\frac {\omega_2} {\sqrt{2 \gamma_2}} - \frac{\dot \lambda} {\gamma_2}) \nonumber \end{align} V˙≤−nV21+γ11(λ−λ∗)λ˙+γ21(α−α∗)α˙+2γ1ω1∣λ−λ∗∣+2γ2ω2∣α−α∗∣=−nV21−γ11∣λ−λ∗∣λ˙−γ21∣α−α∗∣α˙+2γ1ω1∣λ−λ∗∣+2γ2ω2∣α−α∗∣=−nV21+∣λ−λ∗∣(2γ1ω1−γ1λ˙)+∣α−α∗∣(2γ2ω2−γ2λ˙)
此时若令
λ˙=ω1γ12\dot \lambda = \omega_1 \sqrt{\frac{\gamma_1}{2}} λ˙=ω12γ1
则
V˙≤−nV12+∣λ−λ∗∣(ω22γ2−α˙γ2)=−nV12+η\dot V \le -nV^{\frac{1}{2}} + |\lambda-\lambda^{*}|(\frac {\omega_2} {\sqrt{2 \gamma_2}} - \frac{\dot \alpha} {\gamma_2}) = -nV^{\frac{1}{2}} + \eta V˙≤−nV21+∣λ−λ∗∣(2γ2ω2−γ2α˙)=−nV21+η
其中
η=∣λ−λ∗∣(ω22γ2−α˙γ2)\eta = |\lambda-\lambda^{*}|(\frac {\omega_2} {\sqrt{2 \gamma_2}} - \frac{\dot \alpha} {\gamma_2}) η=∣λ−λ∗∣(2γ2ω2−γ2α˙)
所以此系统具有李雅普诺夫稳定性,尽管有 η\etaη 存在,系统仍然可以在一定程度上保持稳定,原因在于我们证明了 V˙≤−nV12≤0\dot V \le -nV^{\frac{1}{2}} \le 0V˙≤−nV21≤0 而不是传统的 V˙≤0\dot V \le 0V˙≤0
相关文章:
)
超螺旋滑模控制(STA)
超螺旋滑模控制(Super Twisting Algorithm, STA) 超螺旋滑模控制又称超扭滑模控制,可以说是二阶系统中最好用的滑模控制方法。 系统模型 对于二阶系统可以建立具有标准柯西形式的微分方程组 {x˙1x2x˙2fg⋅u\begin{cases} \dot x_1 x_2 \\ \dot x_2 f g \cdo…...

NX二次开发编译时dll自动数字签名及拷贝
前言 在UG5.0开始,所有基于UG二次开发的DLL都要“签名”后才能被客户端上正版的NX调用。 一、基于C# 开发签名 1、添加资源文件 (1)项目类库上右键–>属性–>资源–>添加资源右边小三角–>添加现有文件–>切换到UG安装目录下…...

教你如何搭建人事OA-薪资管理系统,demo可分享
1、简介1.1、案例简介本文将介绍,如何搭建人事OA-薪资管理。1.2、应用场景根据设置薪资基础及考勤和绩效的数据计算得到各个员工工资详情。2、设置方法2.1、表单搭建1)新建表单【工资表】,字段设置如下;名称类型名称类型人员资料分…...
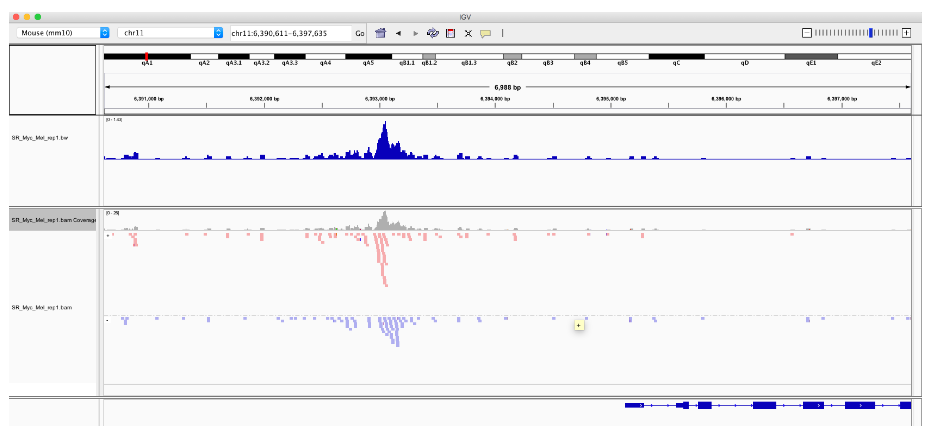
ChIP-seq 分析:Mapped 数据可视化(4)
1. Mapped reads 现在我们有了 BAM 文件的索引,我们可以使用 idxstatsBam() 函数检索和绘制映射读取的数量。 mappedReads <- idxstatsBam("SR_Myc_Mel_rep1.bam")TotalMapped <- sum(mappedReads[, "mapped"])ggplot(mappedReads, aes(x…...
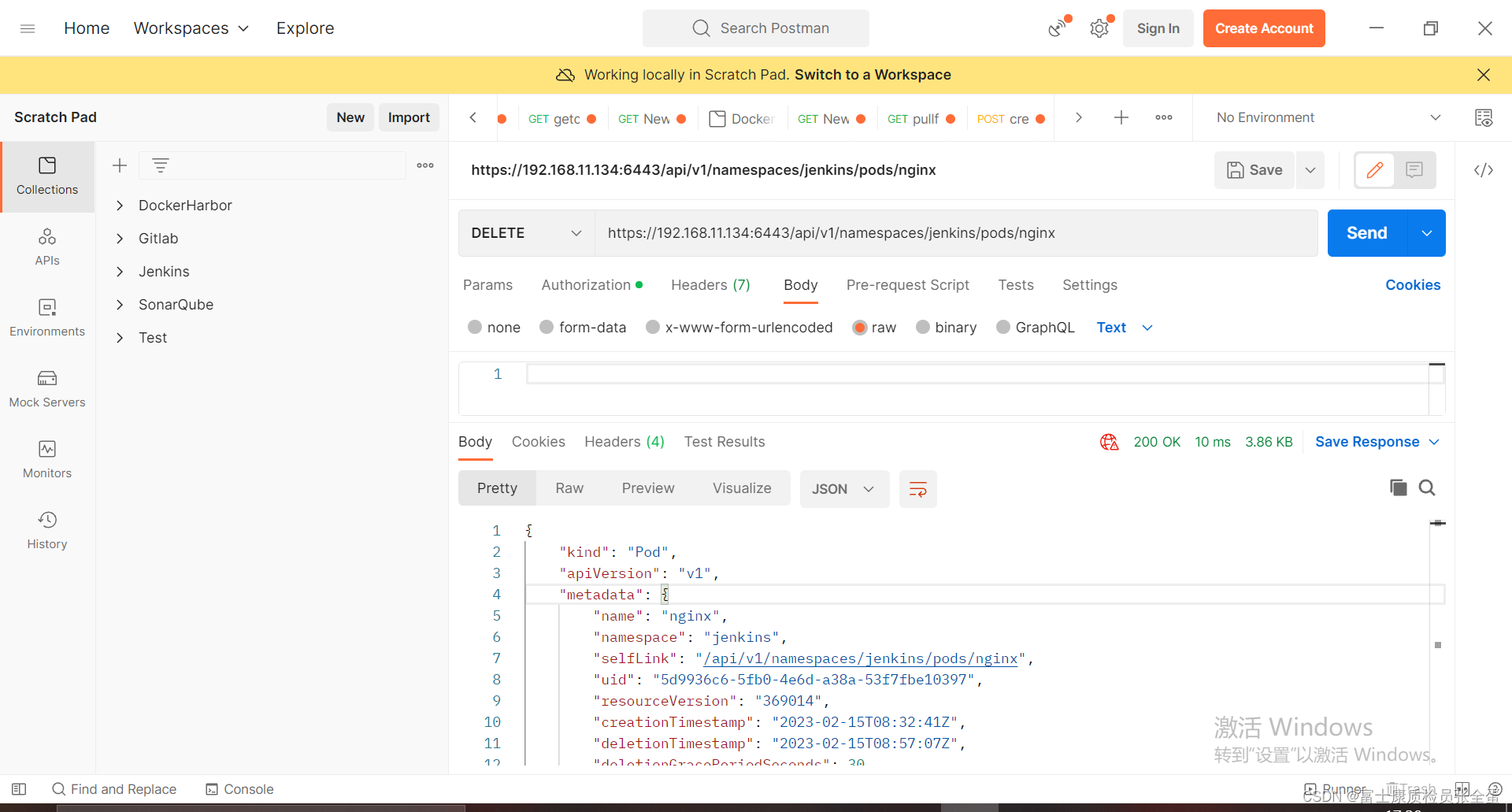
Jenkins 基于Kubernetes 弹性构建池
流程:创建Jenkins Agent;获取Jenkins Agent的参数;渲染yaml模板;调用K8s API在固定的NS中创建一个Pod;运行Jenkins pipeline到agent;创建Agentimport hudson.model.Node.Mode import hudson.slaves.* impor…...

经典算法题---链表奇偶重排(好题)双指针系列
我听别人说这世界上有一种鸟是没有脚的,它只能够一直的飞呀飞呀,飞累了就在风里面睡觉,这种鸟一辈子只能下地一次,那一次就是它死亡的时候。——《阿甘正传》这一文章讲解链表的奇偶排序问题,这是一道不难但是挺好的链…...

数据仓库实战
目录1、最佳实战1.1 表的分类1.2 ETL策略1.3 任务调度2、项目实战2.1 项目概述2.2 数据描述2.3 架构设计2.4 环境搭建2.5 项目开发1、最佳实战 1.1 表的分类 维度建模中表的类型:事实表和维度表 事实表又可以分为:事务事实表、周期快照事实表、累积快照…...

GPT系列:GPT, GPT-2, GPT-3精简总结 (模型结构+训练范式+实验)
😄 花一个小时快速跟着 人生导师-李沐 过了一遍GPT, GPT-2, GPT-3。下面精简地总结了GPT系列的模型结构训练范式实验。 文章目录1、GPT1.1、模型结构:1.2、范式:预训练 finetune1.3、实验部分:2、GPT-22.1、模型结构2.2、范式:预…...

ASE12N65SE-ASEMI高压MOS管ASE12N65SE
编辑-Z ASE12N65SE在ITO-220AB封装里的静态漏极源导通电阻(RDS(ON))为0.68Ω,是一款N沟道高压MOS管。ASE12N65SE的最大脉冲正向电流ISM为48A,零栅极电压漏极电流(IDSS)为10uA,其工作时耐温度范围为-55~150摄氏度。ASE…...
)
centos8防火墙命令配置(开放端口)
查看防火墙状态:(root用户)firewall-cmd –state启动防火墙:(root用户)systemctl start firewalld.service查看防火墙开放端口:(root用户) firewall-cmd --list-ports …...

Instagram营销教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Instagram营销初学者教程 - 从简单和简单的步骤学习Instagram营销从基本到高级概念,包括概述,业务战略,安装和注册,发布和参与,活动审查,微调内容,营销工具和应用程序,集成…...

HTTP Code含义
HTTP Code描述详细100继续100(继续)状态代码表示一个已收到请求,尚未被拒绝服务器。服务器打算在请求已完全收到并已采取行动。当请求包含 Expect 标头字段时100-continue expectation,100响应表示服务器希望接收请求有效负载主体…...
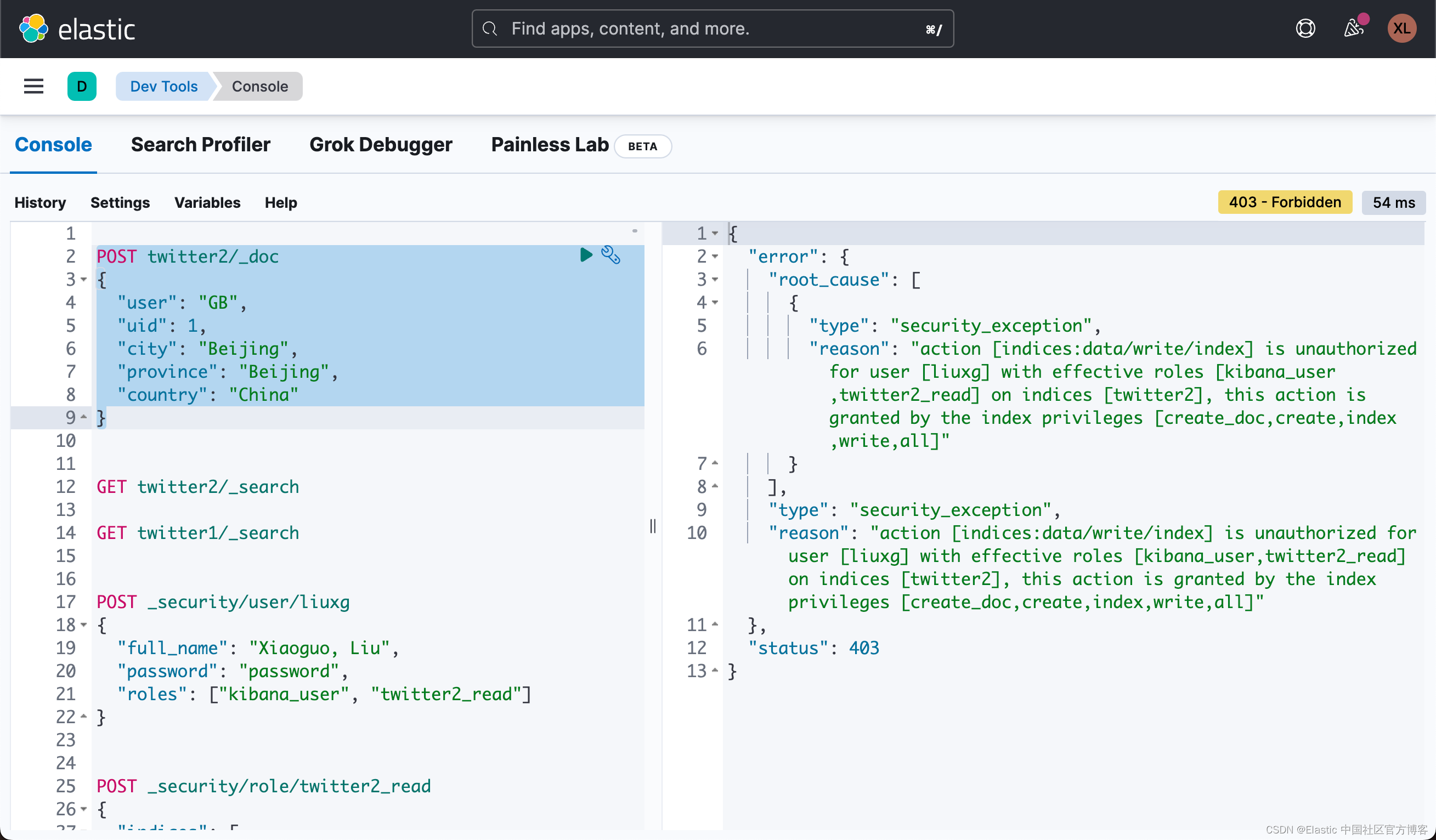
Elasticsearch:Security API 介绍
在我之前的文章 “Elasticsearch:运用 API 创建 roles 及 users” ,我展示了如何使用 Security API 来创建用户及角色来控制访问 Elasticsearch 中的索引。在今天的文章中,我将展示一个使用 Security API 来创建一个用户及角色来访问一个索引…...
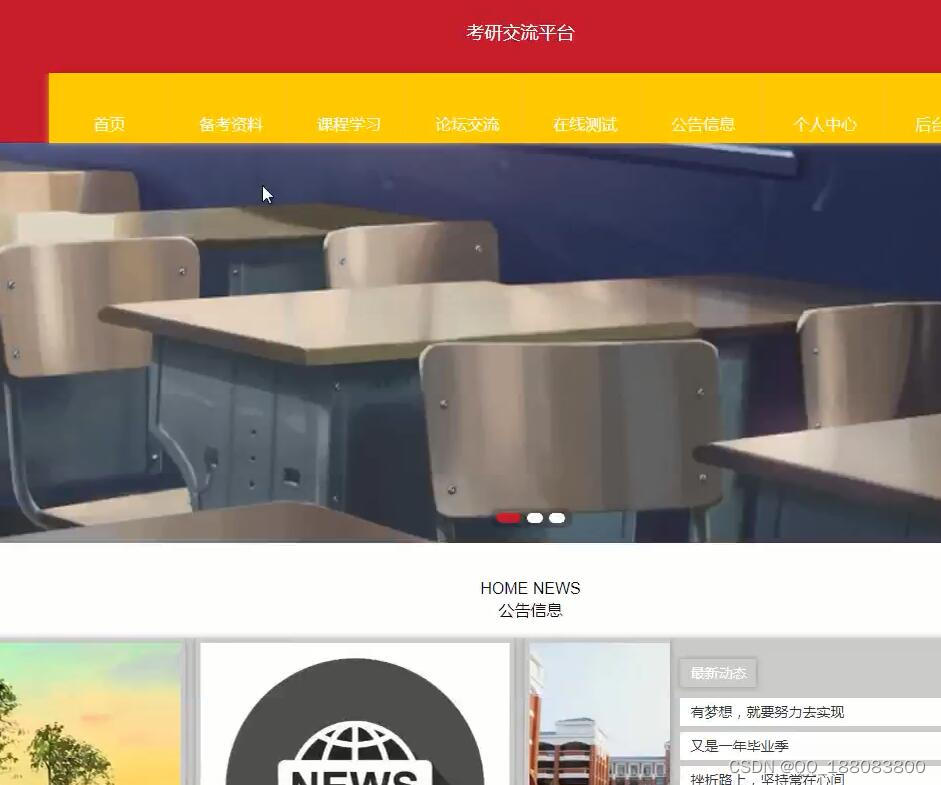
springmvc考研交流平台 java ssm mysql
随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,考研交流平台当然也不能排除在外,从备考资料、课程学习的统计和分析,在过程中会产生大量的、各种各样的…...

2.15 vue3 day01 setup ref setup的参数 prop slot插槽 自定义事件通信
二、常用 Composition API 官方文档: 组合式 API 常见问答 | Vue.js 1.拉开序幕的setup 理解:Vue3.0中一个新的配置项,值为一个函数。 setup是所有Composition API(组合API)“ 表演的舞台 ”。 组件中所用到的:数据…...

CentOs7更新Yum源
1.安装wget yum install -y wget 2.备份配置文件 mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.bak 3.下载国内yum源文件(centOs7,比如阿里) wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.al…...
【C/C++】VS2019下C++生成DLL并且成功调用(金针菇般细)
目录 一,生成动态链接库 二,使用动态链接库 一,生成动态链接库 1.打开VS2019,创建新项目,选择 动态链接库(DLL) 模板后进行下一步 2.输入项目名称,其它默认就行(可自行选择),点击创建 3 工程…...

如何重新安装安卓手机系统
下载并安装您设备的驱动程序和ADB工具。如果您已经拥有了它们,请跳过此步骤。没有就百度下载。 打开终端或命令提示符,并将其设置为包含ADB二进制文件的目录。 启动设备并将其连接到计算机上。 在终端或命令提示符中运行以下命令以确认设备是否连接成…...
ArcGIS API for JavaScript 4.15系列(7)——Dojo中的Ajax请求操作
1、前言 作为重要的前后端交互技术,Ajax被广泛应用于Web项目中。无论是jQuery时代的$.ajax还是Vue时代下的axios,它们都对Ajax做了良好的封装处理。而Dojo也不例外,开发者使用dojo/request模块可以轻松实现Ajax相关操作,下面开始…...
智慧校园电子班牌系统
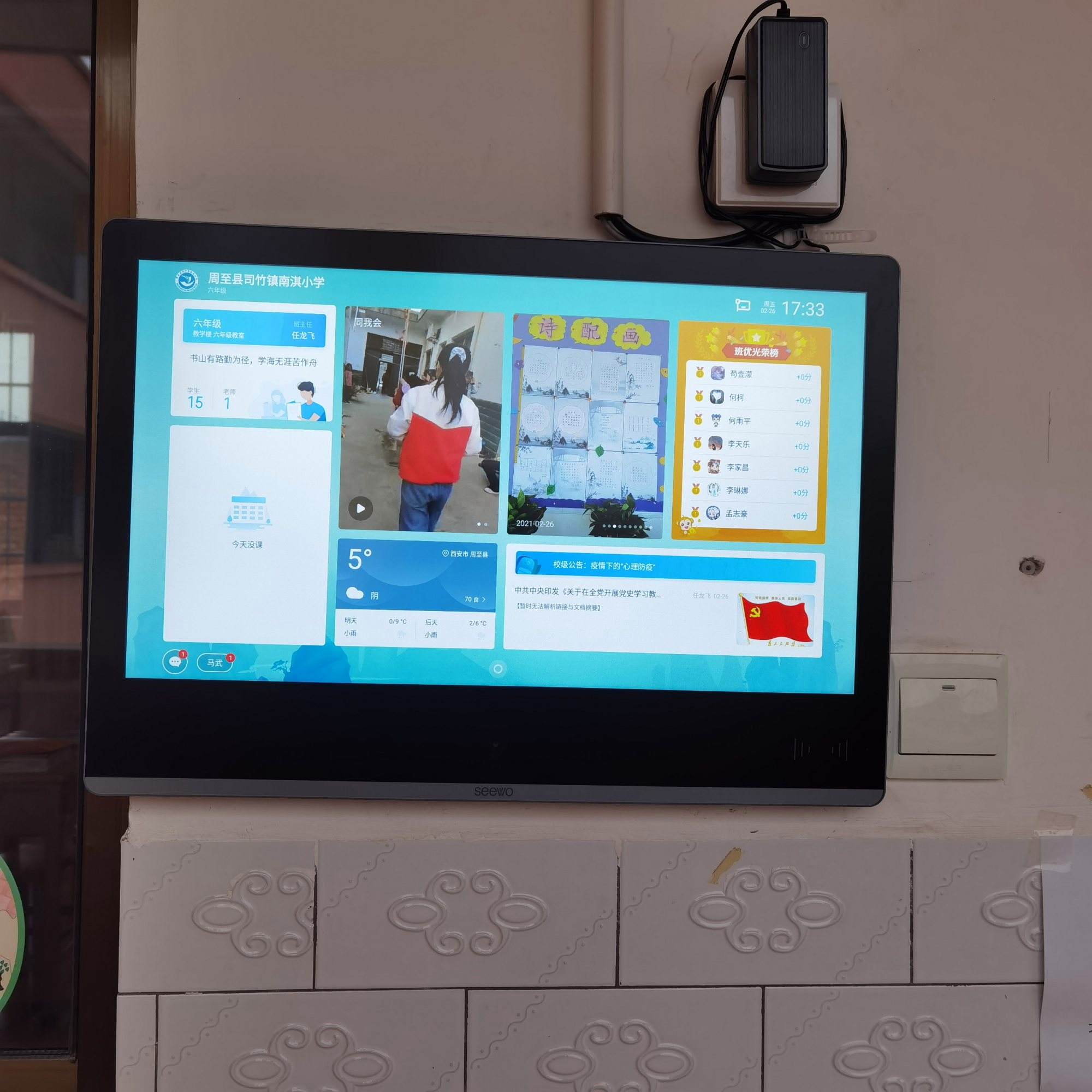
智慧电子班牌区别于传统电子班牌,智慧校园电子班牌系统更加注重老师和学生的沟通交流和及时数据交互。学校为每个教室配置一台智能电子班牌,一般安装于教室门口,用来实时显示学校通知、班级通知,可设置集中分布式管理,…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
