C#,码海拾贝(28)——求解“对称正定方程组”的“平方根法”之C#源代码
using System;
namespace Zhou.CSharp.Algorithm
{
/// <summary>
/// 求解线性方程组的类 LEquations
/// 原作 周长发
/// 改编 深度混淆
/// </summary>
public static partial class LEquations
{
/// <summary>
/// 求解对称正定方程组的平方根法
/// </summary>
/// <param name="mtxLECoef">指定的系数矩阵</param>
/// <param name="mtxLEConst">指定的常数矩阵</param>
/// <param name="mtxResult">Matrix引用对象,返回方程组解矩阵</param>
/// <return>bool 型,方程组求解是否成功</return>
public static bool GetRootsetCholesky(Matrix mtxLECoef, Matrix mtxLEConst, Matrix mtxResult)
{
int i, j, k, u, v;
// 方程组属性,将常数矩阵赋给解矩阵
Matrix mtxCoef = new Matrix(mtxLECoef);
mtxResult.SetValue(mtxLEConst);
int n = mtxCoef.GetNumColumns();
int m = mtxResult.GetNumColumns();
double[] pDataCoef = mtxCoef.GetData();
double[] pDataConst = mtxResult.GetData();
// 非对称正定系数矩阵,不能用本方法求解
if (pDataCoef[0] <= 0.0)
{
return false;
}
pDataCoef[0] = Math.Sqrt(pDataCoef[0]);
for (j = 1; j <= n - 1; j++)
{
pDataCoef[j] = pDataCoef[j] / pDataCoef[0];
}
for (i = 1; i <= n - 1; i++)
{
u = i * n + i;
for (j = 1; j <= i; j++)
{
v = (j - 1) * n + i;
pDataCoef[u] = pDataCoef[u] - pDataCoef[v] * pDataCoef[v];
}
if (pDataCoef[u] <= 0.0)
{
return false;
}
pDataCoef[u] = Math.Sqrt(pDataCoef[u]);
if (i != (n - 1))
{
for (j = i + 1; j <= n - 1; j++)
{
v = i * n + j;
for (k = 1; k <= i; k++)
{
pDataCoef[v] = pDataCoef[v] - pDataCoef[(k - 1) * n + i] * pDataCoef[(k - 1) * n + j];
}
pDataCoef[v] = pDataCoef[v] / pDataCoef[u];
}
}
}
for (j = 0; j <= m - 1; j++)
{
pDataConst[j] = pDataConst[j] / pDataCoef[0];
for (i = 1; i <= n - 1; i++)
{
u = i * n + i;
v = i * m + j;
for (k = 1; k <= i; k++)
{
pDataConst[v] = pDataConst[v] - pDataCoef[(k - 1) * n + i] * pDataConst[(k - 1) * m + j];
}
pDataConst[v] = pDataConst[v] / pDataCoef[u];
}
}
for (j = 0; j <= m - 1; j++)
{
u = (n - 1) * m + j;
pDataConst[u] = pDataConst[u] / pDataCoef[n * n - 1];
for (k = n - 1; k >= 1; k--)
{
u = (k - 1) * m + j;
for (i = k; i <= n - 1; i++)
{
v = (k - 1) * n + i;
pDataConst[u] = pDataConst[u] - pDataCoef[v] * pDataConst[i * m + j];
}
v = (k - 1) * n + k - 1;
pDataConst[u] = pDataConst[u] / pDataCoef[v];
}
}
return true;
}
}
}
相关文章:
C#,码海拾贝(28)——求解“对称正定方程组”的“平方根法”之C#源代码
using System; namespace Zhou.CSharp.Algorithm { /// <summary> /// 求解线性方程组的类 LEquations /// 原作 周长发 /// 改编 深度混淆 /// </summary> public static partial class LEquations { /// <summary> /…...

碳纤维单丝外径测试中的纳米分辨率激光衍射法解决方案
摘要:碳纤维单丝热膨胀系数是碳纤维复合材料设计、生产与可靠性和寿命评估的重要参数,本文针对单丝径向高温热膨胀系数测试这一难题提出了相应的解决方案。解决方案的核心内容是基于激光衍射法和高温辐射加热,并采用衍射轮廓拟合技术以及相应…...

服务(第三十二篇)nginx做缓存服务器
nginx作为缓存服务配置语法 1、proxy_cache_path 配置语法(即缓存路径配置语法) Syntax:proxy_cache_path path [levelslevels] [use_temp_pathon|off] keys_zonename:size [inactivetime] [max_sizesize] [manager_filesnumber] [manager_s…...
Java 集合、数组、字符串的相互转换(关于list.toArray(new String[0])的源码分析)
在 Java 中,可以通过以下方式实现集合、数组和字符串之间的相互转换。 一、集合和数组的相互转化 ①、将集合转为数组:(toArray 方法) List<String> list new ArrayList<>(); list.add("apple"); lis…...
Redis的全局命令及相关误区
Redis中所说的数据结构是针对key-value中的value而言的。主要的结构包括String、哈希表、列表、集合等等在redis中存在16个库,涉及到后期的集群搭建只能使用0号库最为方便 查看所有键(支持通配符) keys * keys S*返回当前数据库中的键总数 …...

C++核心编程—类和对象,类的三大特性——封装、继承、多态
纵有疾风起,人生不言弃。本文篇幅较长,如有错误请不吝赐教,感谢支持。 💬文章目录 一.类和对象的概念①什么是对象?②抽象和类1.类的基本概念2.类的声明与定义:3.对象的创建与使用 二.类的封装①为什么有封…...

keep-alive 是 Vue 内置的一个组件,被用来缓存组件实例。
文章目录 简介注意点使用 keep-alive 有以下优缺点优点缺点 简介 keep-alive 是 Vue 内置的一个组件,被用来缓存组件实例。 使用 keep-alive 包裹动态组件时,被包裹的组件实例将会被缓存起来,而不会被销毁,直到 keep-alive 组件…...

(八)Spring之IOC控制反转、DI依赖注入介绍和使用(详解)
文章目录 前言SpringSpring IOC 简介BeanIOC 概述IOC 本质理解 Spring IOC 应用IOC xml装配IOC 依赖注入IOC Bean的作用域 IoC 自动装配Bean 的自动装配注解实现自动装配 IoC 使用注解开发模拟实现Spring IoC 前言 “Spring”在不同的上下文中表示不同的事物。它可以用来引用 …...
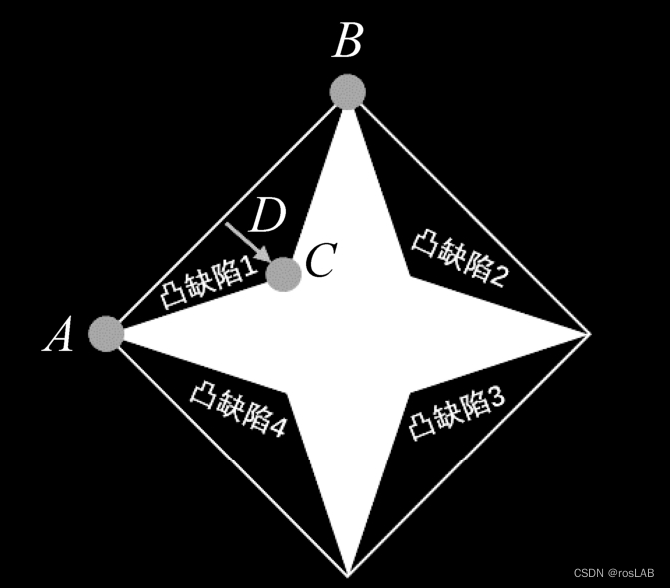
凸缺陷 convexityDefects
获取凸包,可以参考我的这篇文章: 凸包(Convex Hull)代码实现案例 获取了凸包之后,可以干什么呢? 凸缺陷凸包与轮廓之间的部分称为凸缺陷。凸缺陷可用来处理手势识别等问题。 通常情况下,使用如…...

c语言编程练习题:7-43 Shuffling Machine
Shuffling is a procedure used to randomize a deck of playing cards. Because standard shuffling techniques are seen as weak, and in order to avoid “inside jobs” where employees collaborate with gamblers by performing inadequate shuffles, many casinos empl…...

ffmpeg enum AVChannel枚举解析
AVChannel枚举是在2022-12-20的提交中添加的,对应的版本号是5.1. 这个提交的描述是"avutil/channel_layout: add AVChannel enum and related functions"。 原型 typedef struct AVChannelCustom {enum AVChannel id;char name[16];void *opaque; } AVCh…...

invest模型教程
详情点击链接:invest模型教程——建议收藏 1.生态系统服务 2.InVEST模型 3.InVEST所需数据(分辨率、格式、投影系统等)、获取及标准化预处理 4.InVEST运行 5.ArcGIS工具支撑InVEST模型 5.1ArcGIS数据形式与数据格式、数据格式之间的相互转换…...
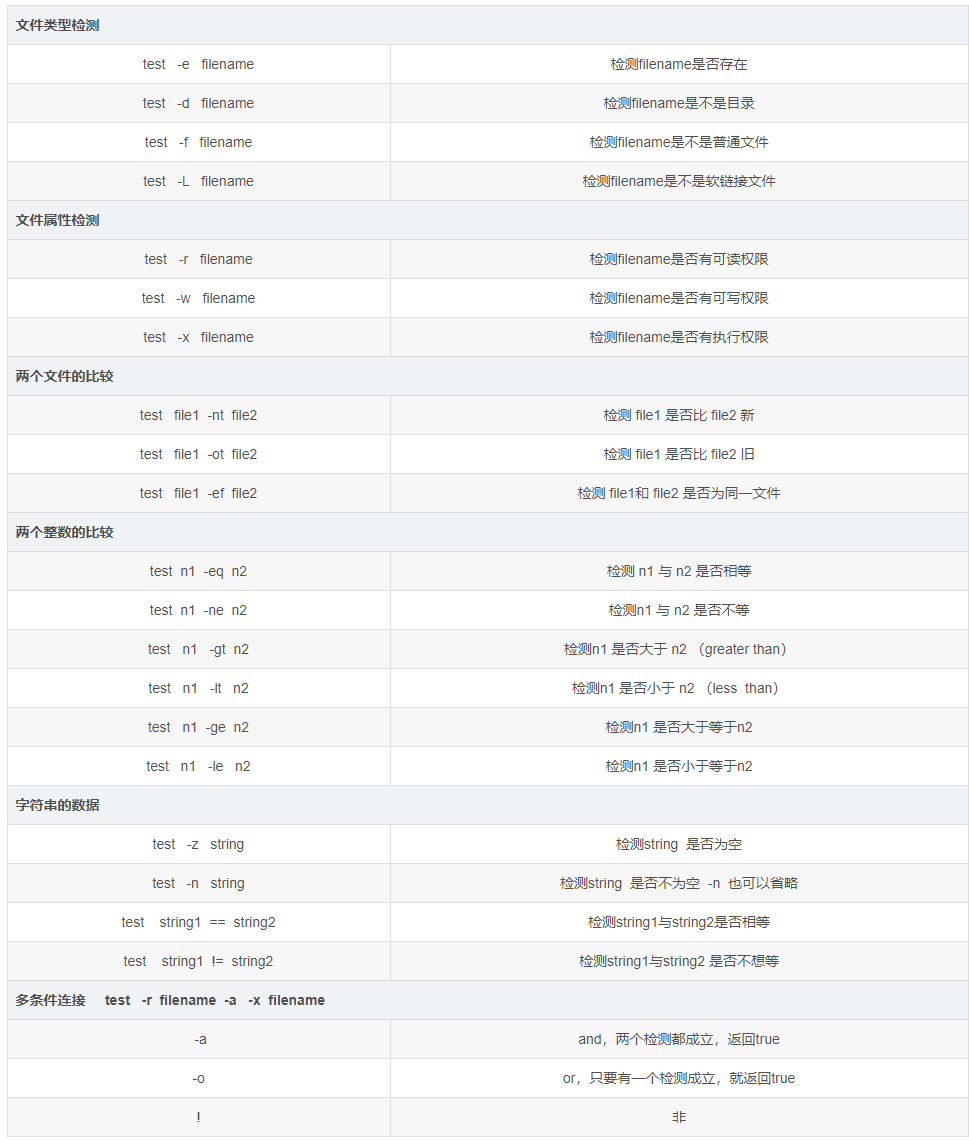
LinuxShell编程
Shell编程 Shell的概念介绍 命令解释器 Shell是命令解释器(command interpreter),是Unix操作系统的用户接口,程序从用户接口得到输入信息,shell将用户程序及其输入翻译成操作系统内核(kernel)能够识别的指令&#x…...
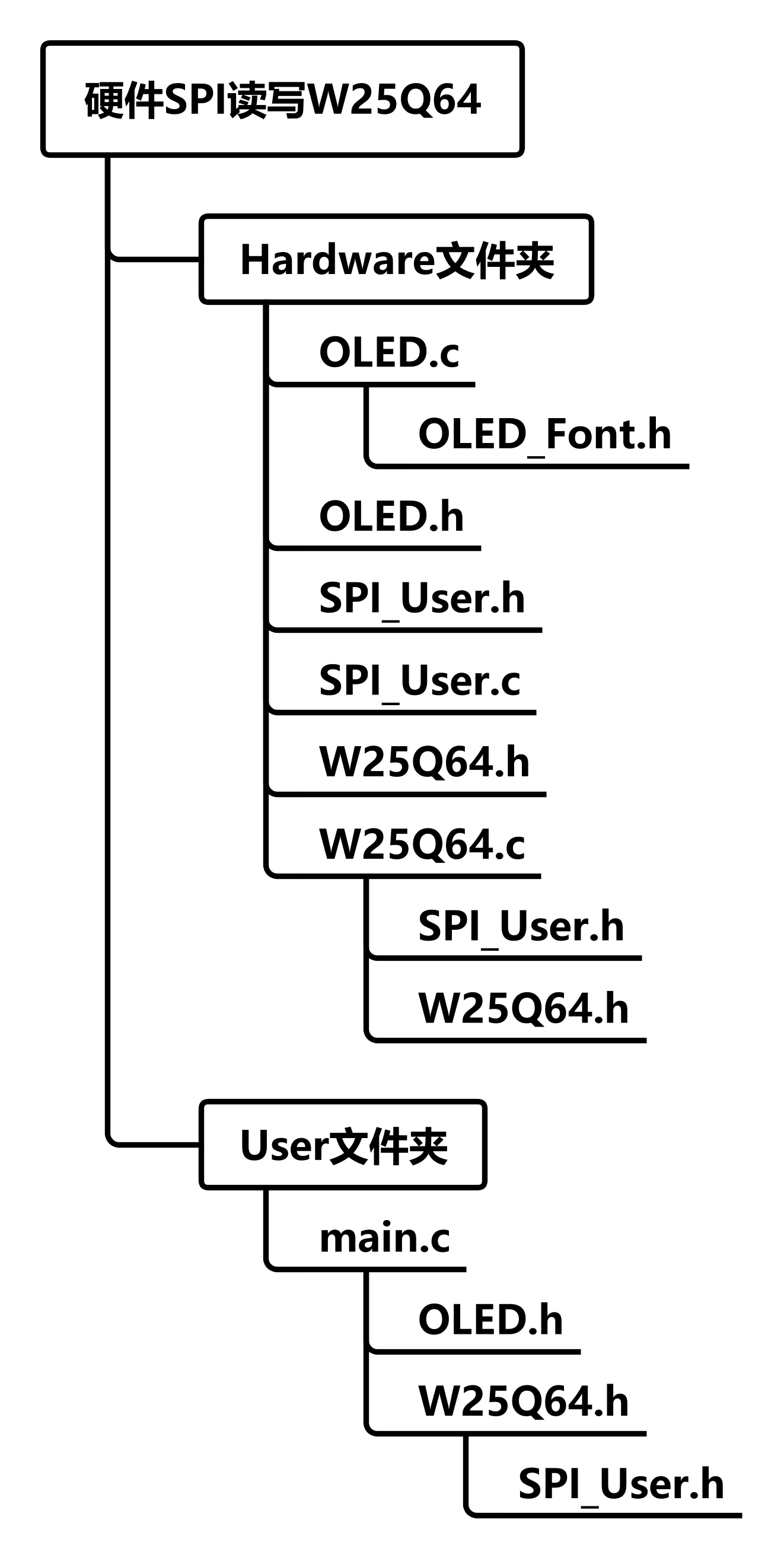
stm32学习笔记-11 SPI通信
11 SPI通信 文章目录 11 SPI通信11.1 SPI通信协议11.2 W25Q64简介11.3 实验:软件SPI读写W25Q6411.4 SPI通信外设11.5 实验:硬件SPI读写W25Q64 注:笔记主要参考B站 江科大自化协 教学视频“ STM32入门教程-2023持续更新中”。 注:…...
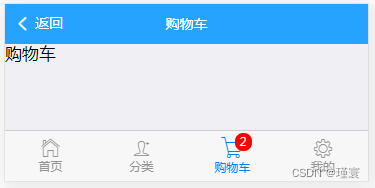
“微商城”项目(3页面布局)
1.设置标题 设置页面头部标题,方便告诉用户当前显示的是哪一个页面。编辑src\router.js文件,示例代码如下。 routes: [{ path: /, redirect: /home, meta: { title: 首页 } },{ path: /home, component: Home, name: home, meta: { title: 首页 } } ] …...

Java 八股文 - MySQL
MySQL 1. MySQL 有几种锁? 三种锁的特点 表级锁:开销小,加锁快;不会出现死锁;锁定颗粒度大,发生锁冲突的概率最高,并发度最低。行级锁:开销大,加锁慢;会…...
周赛347(模拟、思维题、动态规划+优化)
文章目录 周赛347[2710. 移除字符串中的尾随零](https://leetcode.cn/problems/remove-trailing-zeros-from-a-string/)模拟 [2711. 对角线上不同值的数量差](https://leetcode.cn/problems/difference-of-number-of-distinct-values-on-diagonals/)模拟 [2712. 使所有字符相等…...

String AOP的使用
面向切面编程,面向特定方法编程,以方法为对象,在不修改原方法的基础上,对方法进行操作扩展等,底层是通过动态代理实现的 使用开发步骤: 1、创建一个类,加上Aspect声明为一个AOP切面类ÿ…...
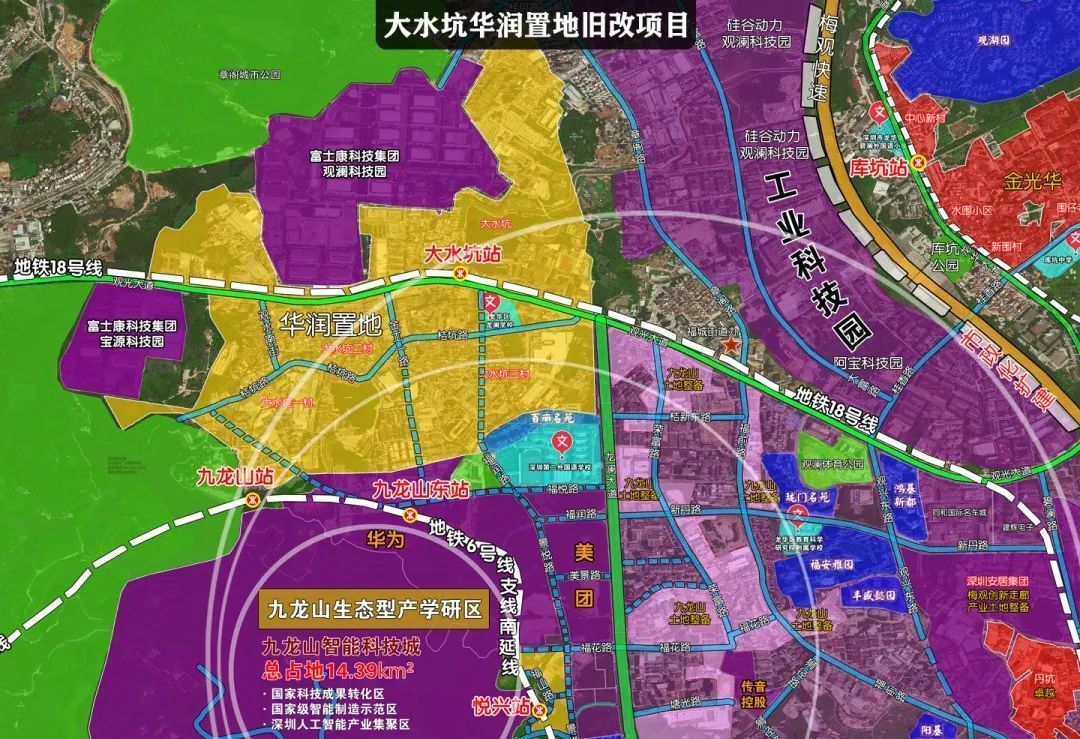
华为芯片基地旁,龙华科技小镇大水坑片区城市更新单元旧改项目
项目位置:龙华观澜大水坑社区,位于梅观创新走廊九龙山产学研片区内 占地面积:总面积198万平方米,其中项目第一期60万平米开 发 商: 华润集团申报主体:华润置地项目:龙华科技小镇大水坑片区城市…...

论文阅读 | 频谱监测、认知电子战、网电攻击
文章目录 1.《超短波信号的频谱监测与信号源定位》1.1 信号预处理技术1.2 对指定频段的宽带信号截获、分析以及频率分选研究1.3 对指定频段的信号进行最佳分频段扫描分析并还原原信号1.4 总结2.《认知电子战理论及关键技术研究》2.1 认知电子战发展现状2.2 认知电子战发展趋势分…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...
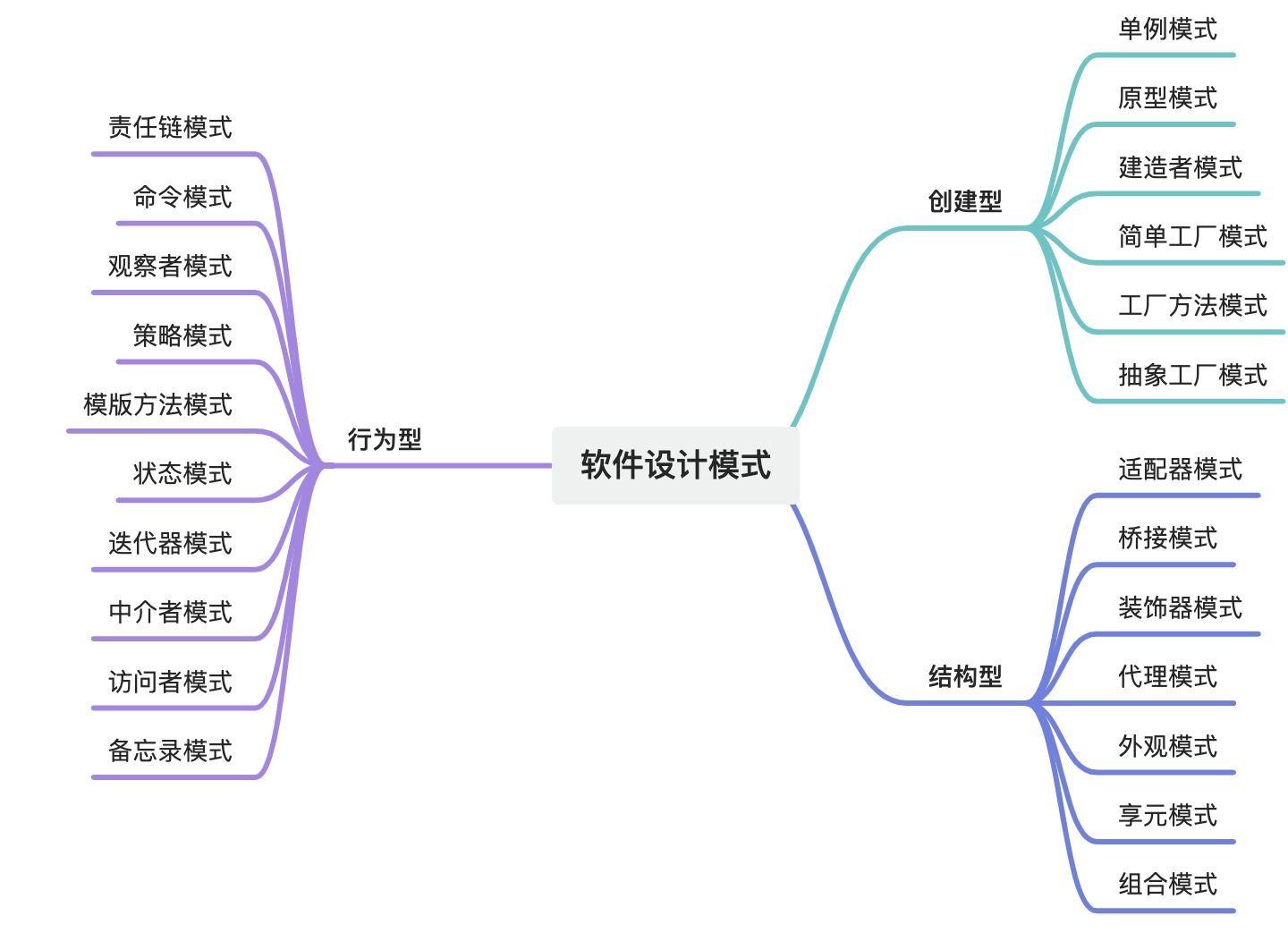
设计模式域——软件设计模式全集
摘要 软件设计模式是软件工程领域中经过验证的、可复用的解决方案,旨在解决常见的软件设计问题。它们是软件开发经验的总结,能够帮助开发人员在设计阶段快速找到合适的解决方案,提高代码的可维护性、可扩展性和可复用性。设计模式主要分为三…...

【AI学习】wirelessGPT多任务无线基础模型摘要
收看了关于WirelessGPT多任务无线基础模型的演讲视频,边做一个记录。 应该说,在无线通信大模型的探索方面,有一个非常有益的尝试。 在沈学明院士带领下开展 https://www.chaspark.com/#/live/1125484184592834560...
