论文笔记:Normalizing Flows for Probabilistic Modeling and Inference
Abstract
- 正则流(Normalizing flows)提供了一种通用的机制来定义富有表达力的概率分布,只需要指定一个(通常简单的)基础分布和一系列可逆变换。
Intraduction
- 正则流通过将简单的密度通过一系列变换来产生更丰富、可能更多模态的分布,就像液体流经一组管道一样运作。
- 灵活性意味着正则流非常适合用于建模、推断和模拟这些关键的统计任务。
- 我们对正则流的探索旨在揭示那些将指导它们在可预见的未来进行构建和应用的持久原则。
- Section 2: 建立正则流的形式和概念结构。
- Section 3 :有限正则流结构(finite);Section 4:极微小变体(infinitesimal variant)。
Section 2:正则流(Normalizing Flow)
2.1 定义和基础
- 规定 x 是 D 维的真实向量,流模型的主要思想是使用从 p u ( u ) p_u(u) pu(u)中采样的真实向量u通过变换T表达x。
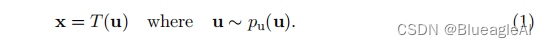
我们规定 p u ( u ) p_u(u) pu(u)是流模型的基本分布。用参数{φ, ψ}分别表示T与 p u ( u ) p_u(u) pu(u),也就引出了由{φ, ψ}定义在x上的分布组。
- 流模型的基本属性是T必须可逆,T与 T − 1 T^{-1} T−1可微,由此也可以推得:

等价的,可以得到:
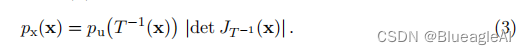
雅可比矩阵(Jacobian)为:

- 在实践中,我们通常用神经网络构建T,并且选取一个简单的密度函数,如多元正态分布,来构建 p u ( u ) p_u(u) pu(u)。在Section 3和4中会讨论如何实施(implement) T。
- 我们可以将变换T看作是对空间R^D的扭曲,以将密度函数pu(u)塑造成px(x)。绝对雅可比行列式|det JT(u)|量化了由于T引起的u周围小邻域的体积相对变化。简单来说,假设du是u周围的(无限小的)小邻域,dx是du映射到的x周围的小邻域。我们可以得到 ∣ d e t J T ( u ) ∣ ≈ V o l ( d x ) / V o l ( d u ) |det J_T(u)| ≈ Vol(dx)/Vol(du) ∣detJT(u)∣≈Vol(dx)/Vol(du),即dx的体积除以du的体积。dx中的概率质量必须等于du中的概率质量。因此,如果du被扩展,那么x处的密度将小于u处的密度。如果du被压缩,那么x处的密度将较大。
- 可逆且可微分的变换的一个重要性质是它们是可组合的。给定两个这样的变换T1和T2,它们的复合变换T2 ◦ T1 也是可逆且可微分的。它的逆变换和雅可比行列式可以表示为:

- 因此,我们可以通过组合多个更简单的转换实例来构建复杂的转换,而不影响可逆性和可微性的要求,因此也不会失去计算密度 p x ( x ) p_x (x) px(x)的能力。所以"flow"指的是从 p u ( u ) p_u(u) pu(u)中获得一组样本,在经过 T 1 , . . . , T k T_1,...,T_k T1,...,Tk的变换序列时所遵循的轨迹。术语"Normalizing"指的是通过逆变化 T 1 − 1 , . . . , T k − 1 T^{-1}_1,...,T^{-1}_k T1−1,...,Tk−1的流动,将 p x ( x ) p_x(x) px(x)中获得的一组样本转化为预定密度$p_u(u)的一组样本(某种意义上为正则化)。
- 在功能上,基于流的模型提供了两个操作:通过公式1从模型中进行抽样,以及通过公式3评估模型的密度。这些操作具有不同的计算要求。从模型中进行抽样需要能够从 p u ( u ) p_u(u) pu(u)中进行抽样,并计算正向变换T。评估模型的密度需要计算逆变换 T − 1 T^{-1} T−1及其雅可比行列式,并评估 p u ( u ) p_u(u) pu(u)的密度。具体应用将决定需要实施哪些操作以及它们需要多高的效率。我们在Section 3和Section 4讨论了与各种实现选择相关的计算折衷。
2.2 流模型的表达能力
- 在研究流的细节之前,重要的问题是:How expressive are flow-based models? Can they represent any distribution p x ( x ) p_x(x) px(x), even if the base distribution is restricted to be simple?
- 我们将证明,在 p x ( x ) p_x(x) px(x)满足合理条件的情况下,这种通用表示是可能的。具体来说,我们将证明,对于任何一对良好行为的分布 p x ( x ) p_x(x) px(x)(目标分布)和 p u ( u ) p_u(u) pu(u)(基础分布),存在一个可微分同胚能够将 p u ( u ) p_u(u) pu(u)转化为 p x ( x ) p_x(x) px(x)。这个论证是构造性的,并基于Hyvärinen和Pajunen(1999)关于非线性独立成分分析(ICA)存在性的类似证明;更详细的处理可以参考Bogachev等人的研究(2005)。
- 具体证明过程可以看论文,比较长这里就不赘述了。
2.3 使用流模型建模及推理
- 与拟合任何概率模型类似,拟合流模型 p x ( x ; θ ) p_x(x;θ) px(x;θ)到目标分布 p x ∗ ( x ; θ ) p^*_x(x;θ) px∗(x;θ)可以通过最小化他们之间的散度以及差异。这种最小化可以通过优化 θ = {φ, ψ}来实现。
2.3.1 前向KL散度与最大似然估计
- p x ∗ ( x ; θ ) p^*_x(x;θ) px∗(x;θ) 与 p x ( x ; θ ) p_x(x;θ) px(x;θ) 之间的前向KL散度可以写成:

前向KL散度非常适用于我们拥有目标分布样本(或者可以生成样本),但不能直接评估目标密度 p x ∗ ( x ; θ ) p^*_x(x;θ) px∗(x;θ)的情况。假设我们有一组来自 p x ∗ ( x ; θ ) p^*_x(x;θ) px∗(x;θ)的样本 { x n } n = 1 N \{x_n\}^N_{n=1} {xn}n=1N,我们可以通过蒙特卡洛方法估计对于p∗x(x)的期望,如下:
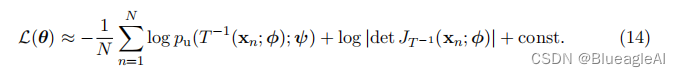
最小化上述蒙特卡洛近似的KL散度等价于通过最大似然估计将基于流的模型拟合到样本 { x n } n = 1 N \{x_n\}^N_{n=1} {xn}n=1N。 - 在实践中,我们通常使用随机梯度下降等方法迭代地优化参数θ。我们可以如下获得对于参数的KL散度梯度的无偏估计:
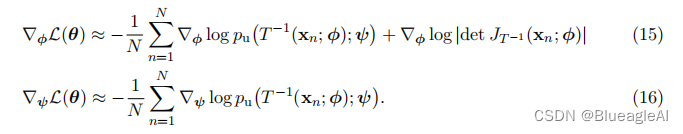
如果 p u ( u ; ψ ) p_u(u; ψ) pu(u;ψ)允许闭式最大似然估计,如高斯分布的情况,那么对于ψ的更新也可以以闭式形式进行。 - 为了通过最大似然方法拟合基于流的模型,我们需要计算 T − 1 T^{-1} T−1、它的雅可比行列式和密度 p u ( u ; ψ ) p_u(u; ψ) pu(u;ψ),以及对这三者进行微分(如果使用基于梯度的优化算法)。这意味着即使我们无法计算T或从pu(u; ψ)中进行抽样,我们仍然可以使用最大似然来训练流模型。然而,如果我们希望在拟合完成后从模型中进行抽样,这些操作将是必需的。
2.3.2 反向KL散度
-
或者,我们可以通过最小化反向KL散度来拟合基于流的模型,它可以写成:
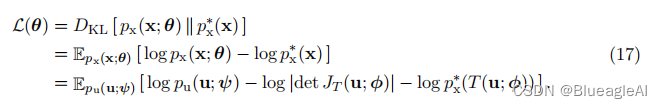
为了表达对于u的期望,我们使用了变量的变换。当我们能够评估目标密度 p x ∗ ( x ) p^*_x(x) px∗(x),但不一定能够从中进行抽样时,反向KL散度是合适的。
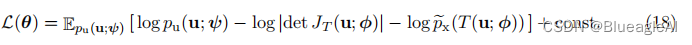
-
在实践中,我们可以使用随机梯度下降等方法迭代地最小化L(θ)。由于我们重新参数化了期望,使其相对于基础分布 p u ( u ; ψ ) p_u(u; ψ) pu(u;ψ),我们可以通过蒙特卡洛方法轻松地获得L(θ)相对于φ的无偏梯度估计。具体而言,假设 { u n } n = 1 N \{u_n\}^N_{n=1} {un}n=1N是从pu(u; ψ)中抽样得到的一组样本,则L(θ)相对于φ的梯度可以如下估计:
为了按照上述描述最小化反向KL散度,我们需要能够从基础分布 p u ( u ; ψ ) p_u(u; ψ) pu(u;ψ)中进行抽样,并计算和对变换T及其雅可比行列式进行微分。这意味着即使我们无法评估基础密度或计算逆变换 T − 1 T^{-1} T−1,我们仍然可以通过最小化反向KL散度来拟合基于流的模型。然而,如果我们想要评估训练模型的密度,我们将需要这些操作。
2.3.3 前向和反向KL散度的关系
(To be continue)
相关文章:
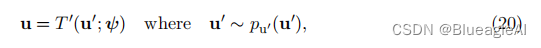
论文笔记:Normalizing Flows for Probabilistic Modeling and Inference
Abstract 正则流(Normalizing flows)提供了一种通用的机制来定义富有表达力的概率分布,只需要指定一个(通常简单的)基础分布和一系列可逆变换。 Intraduction 正则流通过将简单的密度通过一系列变换来产生更丰富、可…...

java 异常类介绍
Java 异常(Exception)是指在程序运行期间出现的错误或异常情况。Java 异常处理机制允许程序在出现异常情况时进行处理,避免程序崩溃或出现不可预知的错误 一、Java 异常的概念 Java 异常是指程序在运行期间出现的错误或异常情况。Java 异常…...
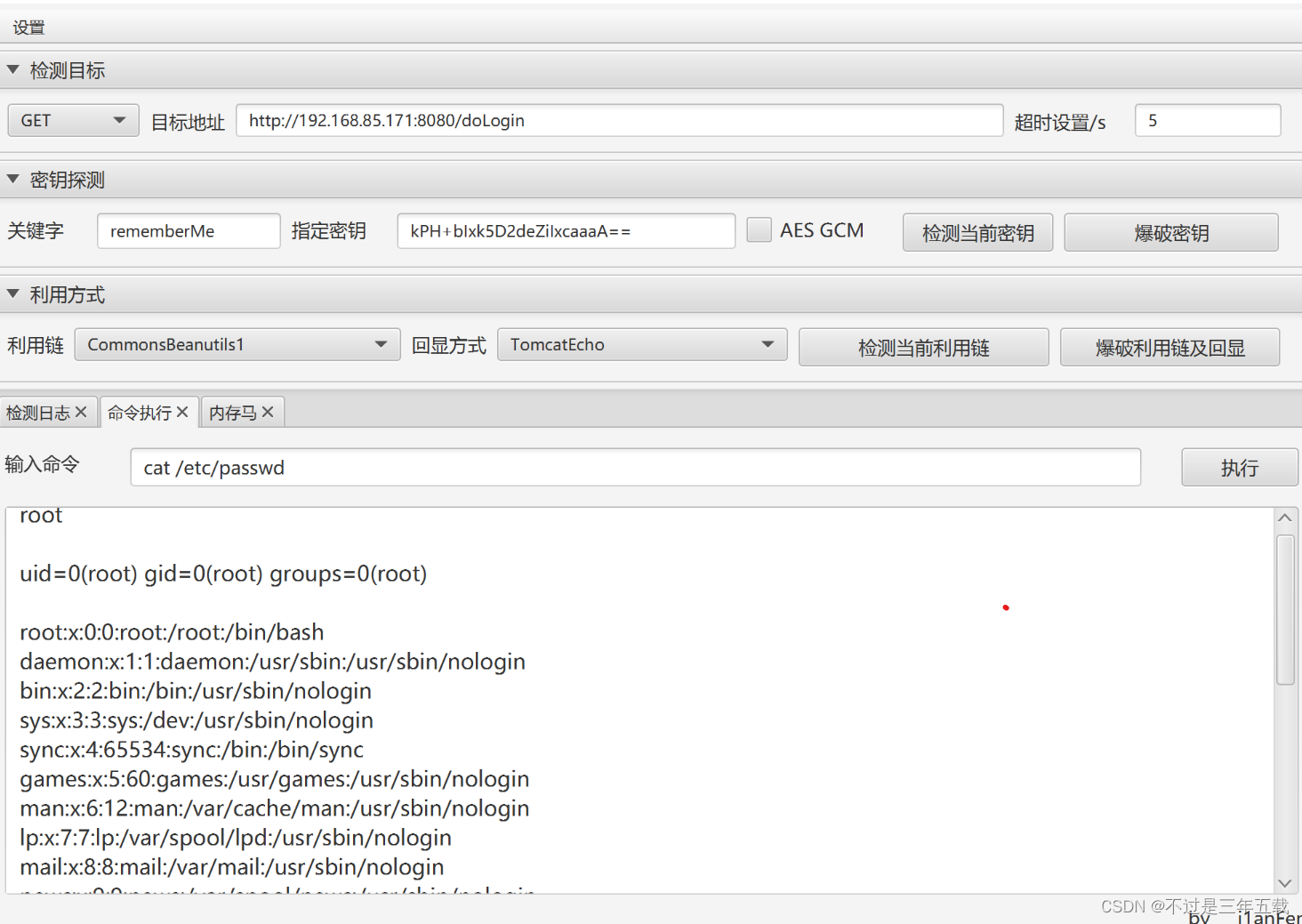
shiro 550 反序列化rce
Apach shiro 是一款开源安全框架,提供身份验证,授权,会话管理等。 shiro 550 反序列化漏洞rce 通关利用它反序列化的漏洞直接执行rce 加密的用户信息序列化后储存在名为remenber -me的cooike中。攻击者可以使用shiro默认密钥伪造cooike&am…...

【C++】---模板初阶(超详练气篇)
个人主页:平行线也会相交💪 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【C之路】💌 本专栏旨在记录C的学习路线,望对大家有所帮助🙇 希望我们一起努力、成长&…...
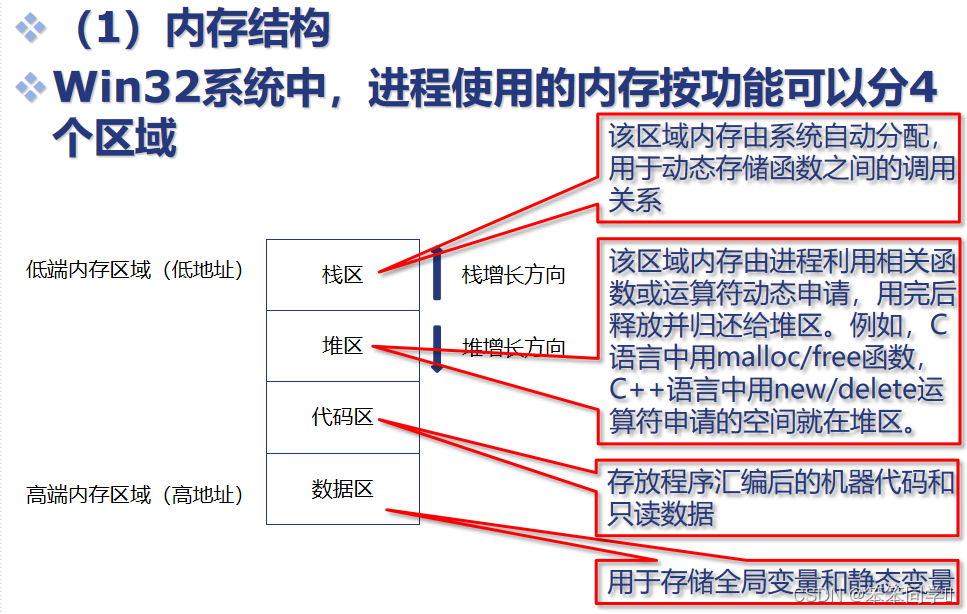
windows系统典型漏洞分析
内存结构 缓冲区溢出漏洞 缓冲区溢出漏洞就是在向缓冲区写入数据时,由于没有做边界检查,导致写入缓冲区的数据超过预先分配的边界,从而使溢出数据覆盖在合法数据上而引起系统异常的一种现象。 ESP、EPB ESP:扩展栈指针(…...

WPF开发txt阅读器:需求分析和文件读写
文章目录 需求分析读取文本文件保存文本文件 需求分析 尽管现在比较主流的阅读格式已经是epub, modi之类的,但txt的使用范围要远比前两者广泛,所以做一个txt阅读器还是有必要的。 但是对于书籍阅读而言,纯文本不包含目录信息,这…...
C++服务器框架开发9——日志系统LogFormatter_4/各个类的关系梳理/std::function/std::get
该专栏记录了在学习一个开发项目的过程中遇到的疑惑和问题。 其教学视频见:[C高级教程]从零开始开发服务器框架(sylar) 上一篇:C服务器框架开发8——日志系统LogFormatter_3/override/宏定义优化switchcase结构 C服务器框架开发9——日志系统LogFormatt…...

arm平台上的MNN编译与运行
0.成果物 直接获取成果物见:https://download.csdn.net/download/u012824853/87867665 以下为编译、运行过程 1.编译准备 在GitHub - alibaba/MNN: MNN is a blazing fast, lightweight deep learning framework, battle-tested by business-critical use cases …...
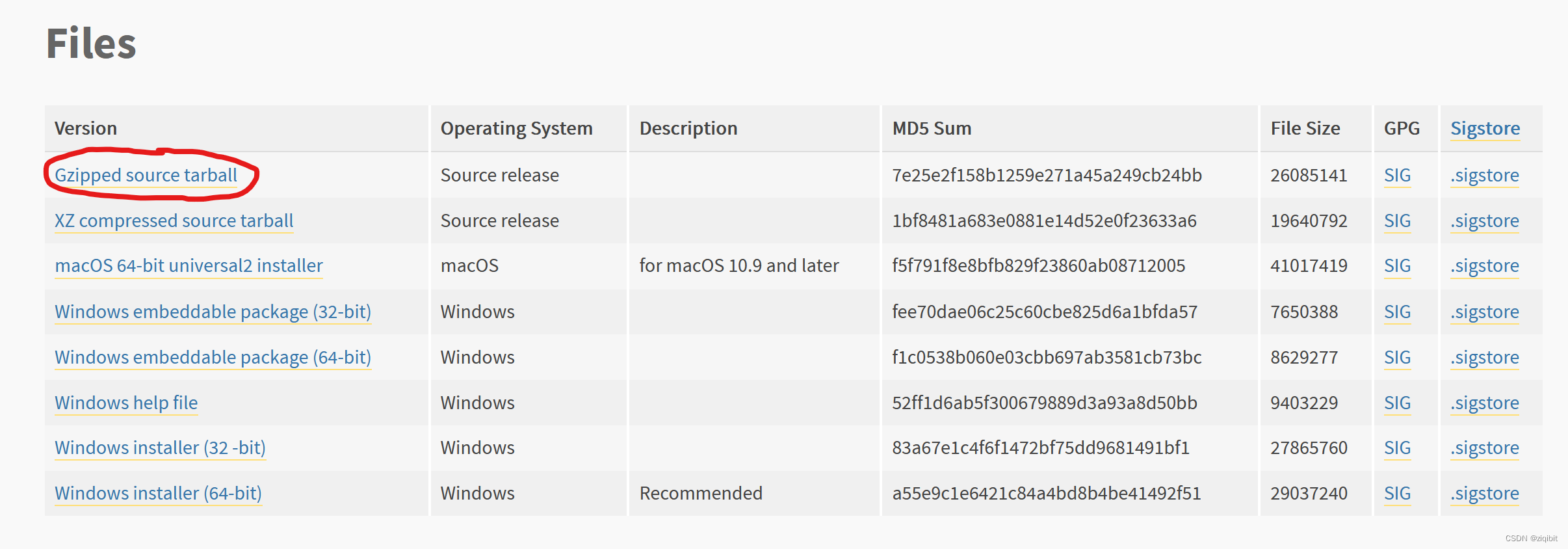
python 编译安装指定版本 for linux
python环境是linux中必备的,部分发行版会自带python,有时候需要安装手动安装 注意:如果需要多个版本并存,建议使用conda环境,如果自己配置多版本,需要用多个软链接 conda环境,可以参考&#x…...

在Linux系统下基于Docker搭建Redis集群
创建镜像 #部署Redis集群,该集群有3个节点; --cluster-enabled yes允许启用集群; docker create --name redis-node--01 --net host -v /data/redis-data/node1:/data redis:5.0.5 --cluster-enabled yes --cluster-config-file redis-node--01.conf --port 6379…...

牛客网刷题Day5
1.内容中可以使用哪个元素来表示 <article> 标签外的内容? A aside B cite C article D class 正确答案:A 解析:<aside> 标签定义 <article> 标签外的内容,aside 的内容应该与附近的内容相关 2. 以下的HTML代码…...

Vue.js 中的动态组件是什么?如何使用动态组件?
Vue.js 中的动态组件是什么?如何使用动态组件? Vue.js是一种流行的前端框架,它提供了一种称为“动态组件”的技术,使得我们可以动态地切换组件的内容和结构。在本文中,我们将深入探讨Vue.js中的动态组件,包…...
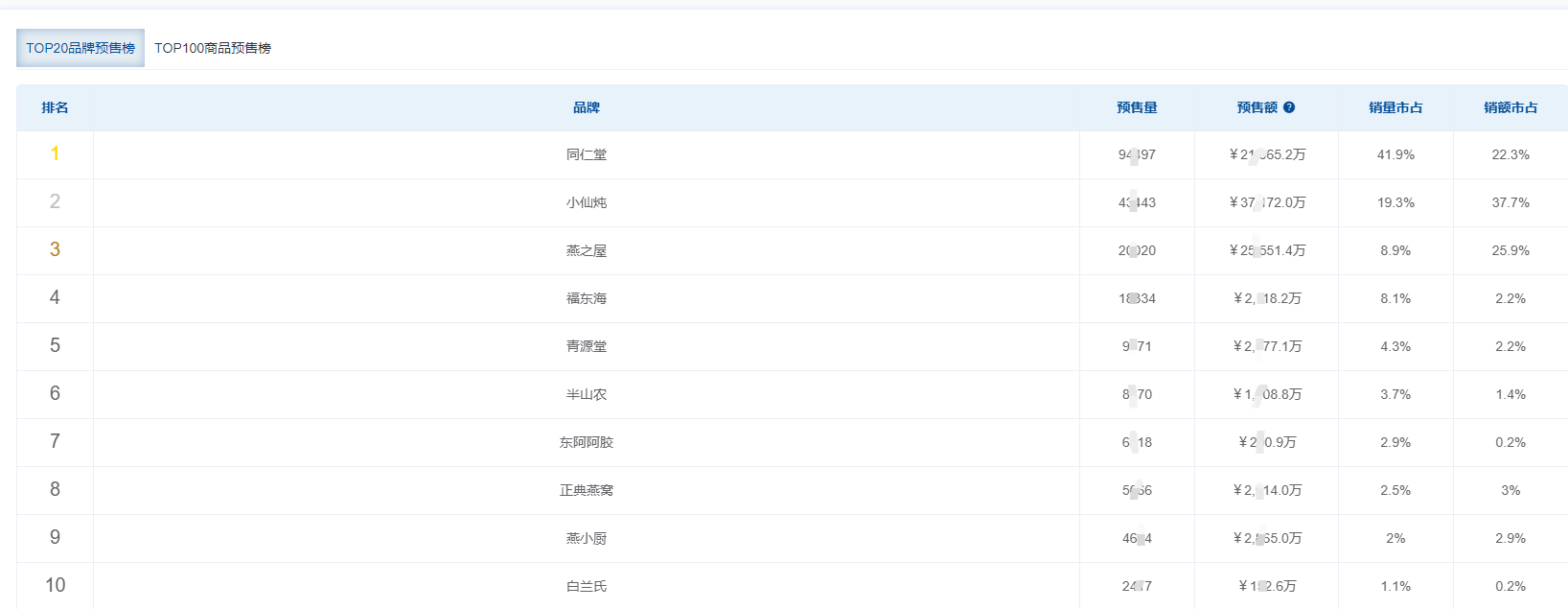
2023年京东618预售数据:传统滋补成预售黑马,预售额超27亿
这一期主要分享一下此次京东618预售期间的一个黑马行业——传统滋补。不管是从预售量和预售额来看,传统滋补品类的成绩都是此次大促中的佼佼者。 究其原因,近几年养生滋补也掀起了一股“国潮风”。在小红书、抖音等社交平台上,关于“健康养生…...

【Linux系统基础快速入门详解】Linux 常用文件过滤编辑命令原理详解和每个命令使用场景以及实例
Linux 文件过滤编辑命令:echo,printf,cat,tee,特殊符号: {a..z},seq序列,rename 文件过滤编辑命令:echo:将字符串输出到终端或文件中。常用于输出环境变量,或者在shell脚本中输出一些提示信息。例如:echo $PATH,输出环境变量PATH的值。printf:格式化输出字符串到终端或文…...

05WEB系统的通信原理图
WEB系统的通信原理 名称作用URL统一资源定位符, 例如:http://www.baidu.com域名在https://www.baidu.com/这个网址中www.baidu.com 是一个域名IP地址计算机在网络当中的一个身份证号, 在同一个网络当中IP地址是唯一的, 有了IP地址两台计算机直接才能建立连接通信端口号一个计算…...

降低试错成本,低代码或成企业数字化转型突破口
近年来,随着市场竞争和宏观环境的双重驱动,数字化已经成为企业提升竞争性和保持可持续发展的重要手段,大多数企业意识到数字化转型的重要性,纷纷入局。 作为数据驱动业务创新的一个新方法,但行业成功的案例并不多&…...
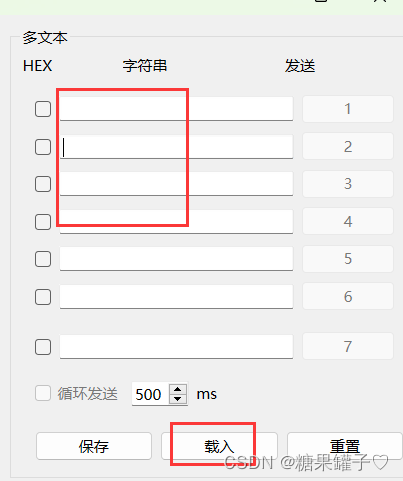
串口助手(串口发送接收数据, 定时, 清空, hex显示)
文章目录 前言一、串口接收数据1. 默认接收,换行,hex显示2. 清空接收区数据3. 保存接受区数据 二、串口发送数据1. 默认发送2. 定时发送 三、串口助手优化1. 设置组合框当前内容。2. 未检测到串口,弹出警告。3. 载入文件 总结 前言 这篇文章…...

bp神经网络
%% 2.读取数据(两个文件) datareadmatrix(C:\Users\Administrator\Desktop\synthetic_01.csv); file_lengthlength(data); for i1:file_length %用for循环去导入第二个csv文件 namedata(i); pathstrcat(C:\Users\Administrator\Desktop\ydata.…...

strace交叉编译后对特定文件的写流程进行监控和过滤
交叉编译 为了支持strace对pid进行解析,因系统默认支持的strace版本较低,需要使用较新的版本对strace进行交叉编译,这里使用了github上的 https://github.com/strace/strace/releases 发布的strace v5.19版本,2022-08-12发布。lo…...
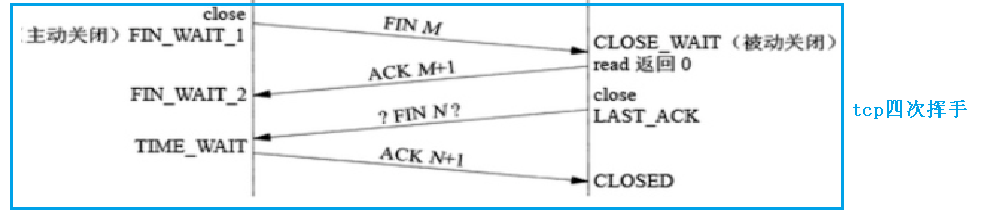
初识网络之TCP网络套接字
目录 一、TCP常用网络接口 1. 监听服务器 2. 接收链接 3. 发起连接 二、实现一个简单的tcp程序 1. 日志函数 2. 服务端文件 2.1 .hpp文件 2.2 .cpp文件 3. 客户端文件 3.1 .hpp文件 3.2 .cpp文件 4. 程序测试 三、实现支持多个用户并发访问的tcp程序 1. 当前程序…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...