算法与数据结构(三)
一、堆
1,堆结构就是用数组实现的完全二叉树结构
根节点的左孩子的下标为:2i+1,右孩子为2i+2。两个孩子的父节点为(i-1)/2向下取整
2,完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
从下往上将孩子与父节点进行比较,如果子叶节点的数值大于根节点,则互换,反之则停止向上比较
3,完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
与大根堆相反
4,堆结构的heapInsert与heapify操作
以上大根堆与小根堆的比较就是heapInsert的过程;
大根堆heapInsert的代码演示:
void heapify(vector<int> &a, int index)
{while (a[index] > a[(index - 1) / 2]){//两个元素互换swap(a, a[index], a[(index - 1) / 2]);//向上反馈index = (index - 1) / 2;}
}
heapify操作:
这里举一个例子,当用户想要删除大根堆中的最大值,我们首先要将数组中最后一个数覆盖到数组中的0位置,然后根节点开始与两个子叶节点的最小值进行互换,然后被换之后再将换下来的根节点与当前位置的两个子叶节点进行比较互换操作。
void heapify(vector<int> &a, int index, int heapsize)
{//index表示从何位置开始进行heapify操作操作//heapsize表示数组的长度//设置左孩子的下标int left = index*2+1;//如果当前根节点还有叶节点,则操作while(left < heapsize){//两个孩子中,谁的值大,则把下标给largestint largest = left + 1 < heapsize && a[left+1] > a[left]? left+1 : left;//父和孩子之间的最大值谁最大,将下标给largestlargest = a[largest] > a[index] ? largest :index;//如果最大值就是根节点,则退出if(largest == index)break;//否则则交换swap(a, index, largest);index = largest;left = index*2+1;}
}
二、堆排序
思路:
1、将数组排列成堆结构,并通过heapInsert操作组成一个大根堆
2、将大根堆的0号位置的节点与最后一个节点互换,heapsize减1,并将堆中最后一个元素放到0位置,进行heapify操作
3、重复2步骤直至堆的大小为0,结束操作
动图展示:

代码实现:
void heapify(vector<int>&a, int index1, int heapsize)
{//进行heapifty//设置左孩子的节点int left = 2 * index1 + 1;//如果有左孩子,则开始进行heapiftywhile (left < heapsize){//如果有右孩子,且右孩子的数值较大,则将右孩子的下标设置为largestint largest = left + 1 < heapsize && a[left + 1] > a[left] ? left + 1 : left;//比较根节点与较大孩子的数值,如果根节点大,则跳出循环if (index1 == largest){break;}//否则互换swap(a, index1, largest);//设置将最大值的下标赋值给index1,继续向下index1 = largest;left = 2 * index1 + 1;}
}void heapInsert(vector<int> &a, int index)
{while (a[index] > a[(index - 1) / 2]){//两个元素互换swap(a, a[index], a[(index - 1) / 2]);//向上反馈index = (index - 1) / 2;}
}void heapSort(vector<int> &a, int heapsize)
{if (a.size() < 2)return;//将数组构建成大根堆for (int i = heapsize-1; i >= 0; i--){heapify(a, i, heapsize);}swap(a, 0, --heapsize);while (heapsize>0){//将变成大根堆的根节点与数组的最后一个数互换,并且将heapsize减小1heapify(a, 0, heapsize);swap(a, 0, --heapsize);}
}
三、堆排序扩展
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。
我们先构建一个元素数量为k的小根堆,因为移动距离最大为k,所以在极端情况下,使用这种方法将小根堆的根节点,也就是最小值放到0位置,然后指针向后移动一个位置,再将数组下表为k的元素放到小根堆内,再次组成一个小根堆,以此类推。最后将小根堆内的数依次从小到大弹出即可。
在c++中,multiset操作的底层就是二叉树的结构。
void SortArrayDistanceLessK(vector<int> &a, int k)
{//定义一个multiset容器multiset<int> s;//设置遍历的起始点int index = 0;//防止k超过数组长度,要限制传入multiset容器的元素数量int c = a.size();int b = min(c, k);for (; index <= b; index++){//将数组的前K个数依次传到multiset容器中s.insert(a[index]);}int i = 0;//依次将K后面的元素传入multiset容器中,并弹出第一个元素for (; index < a.size(); index++){//将k之后的元素一个一个压入到multiset中s.insert(a[index]);//将set的第一个元素放到数组的第一个位置,并将multiset容器第一个元素删除set<int>::const_iterator it = s.begin();a[i] = *it;//删除第一个元素s.erase(s.begin());i++;}//将multiset容器中的数据以此弹出while (!s.empty()){//将set的第一个元素放到数组的第一个位置,并将multiset容器第一个元素删除set<int>::const_iterator it = s.begin();a[i++] = *it;//删除第一个元素s.erase(s.begin());}
}
四、桶排序
基数排序:
c++代码示例
#include <cmath>int getDigit(int x, int d)
{//返回所需位数的数值return((x / (int)pow(10, d - 1)) % 10);
}//桶排序
void radixSort(vector<int> &a, int L, int R, int digit)
//L:要排序的左区域
//R:要排序的右区域
//digit十进制的位数
{//以十为基底int radix = 10;int i = 0, j = 0;//设置辅助空间,其大小与数组大小一致int *bucket = new int[R - L + 1];//有多少位就进出桶多少次,开始入桶for (int d = 1; d <= digit; d++){//count[0]为当前位(d位)是0的数字有多少个//count[1]为当前位(d位)是0-1的数字有多少个//count[2]为当前位(d位)是0-2的数字有多少个//count[i]为当前位(d位)是0-i的数字有多少个//申请一个辅助数组,记录上面的数据int *count = new int[radix];//将申请的内存全部附初值0for (int i = 0; i < radix; i++){count[i] = 0; }//开始入桶操作for (i = L; i <=R; i++){j = getDigit(a[i], d);count[j]++;}//对辅助数组处理成前缀和for (i = 1; i < radix; i++){count[i] = count[i] + count[i - 1];}//开始出桶操作for (i = R; i >= L; i--){j = getDigit(a[i], d);bucket[count[j] - 1] = a[i]; count[j]--;}int j = 0;for (i = L; i <= R; i++){a[i] = bucket[j];j++;}}
}int maxbits(vector<int> &a)
{//定义一个最大数值暂存变量int largest = 0;for (int i = 0; i < a.size(); i++){largest = max(largest, a[i]);}//开始计算最大数值的十进制数一共有多少位int res = 0;while (largest != 0){res++;largest /= 10;}return res;
}void radixSort(vector<int> &a)
{if (a.size() < 2)return;radixSort(a, 0, a.size() - 1, maxbits(a));}
五、排序算法的稳定性及其汇总
同样值的个体之间,如果不因为排序而改变相对次序,就是这个排序是有稳定性的;否则就没有。
不具备稳定性的排序:
选择排序、快速排序、堆排序
具备稳定性的排序:
冒泡排序、插入排序、归并排序、一切桶排序思想下的排序
目前没有找到时间复杂度O(N*logN),额外空间复杂度0(1),又稳定的排序。
 注意!
注意!
1,归并排序的额外空间复杂度可以变成O(1),但是非常难,不需要掌握,有兴趣可以搜“归并排序内部缓存法”。
2,“原地归并排序”会让归并排序的时间复杂度变成o(N^2
)3,快速排序可以做到稳定性问题,但是非常难,不需要掌握,可以搜“01stable sort”
4,所有的改进都不重要,因为目前没有找到时间复杂度0(N*logN),额外空间复杂度0(1),又稳定的排序。
5,有一道题目,是奇数放在数组左边,偶数放在数组右边,还要求原始的相对次序不变,碰到这个问题,很难。
相关文章:

算法与数据结构(三)
一、堆 1,堆结构就是用数组实现的完全二叉树结构 根节点的左孩子的下标为:2i1,右孩子为2i2。两个孩子的父节点为(i-1)/2向下取整 2,完全二叉树中如果每棵子树的最大值都在顶部就是大根堆 从下往上将孩子与父节点进行比较,如果子叶…...

亚马逊云科技出海日,让数字经济出海扩展到更多行业和领域
数字化浪潮之下,中国企业的全球化步伐明显提速。从“借帆出海”到“生而全球化”,中国企业实现了从传统制造业“中国产品”出口,向创新“中国技术”和先导“中国品牌”的逐步升级。 作为全球云计算的开创者与引领者,亚马逊云科技…...

Pb协议的接口测试
【摘要】 Protocol Buffers 是谷歌开源的序列化与反序列化框架。它与语言无关、平台无关、具有可扩展的机制。用于序列化结构化数据,此工具对标 XML ,支持自动编码,解码。比 XML 性能好,且数据易于解析。更多有关工具的介绍可参考…...
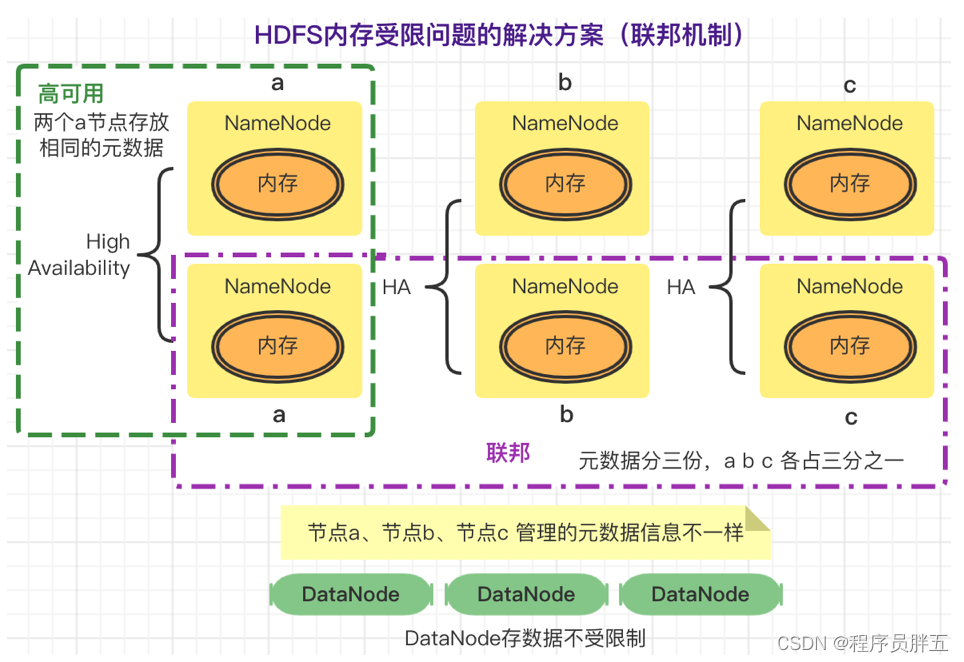
2. 分布式文件系统 HDFS
2. 分布式文件系统 HDFS 1. 引入HDFS【面试点】 问题一:如果一个文件中有 10 个数值,一行一个,并且都可以用 int 来度量。现在求 10 个数值的和 思路: 逐行读取文件的内容把读取到的内容转换成 int 类型把转换后的数据进行相加…...

借助金融科技差异化发展,不一样的“破茧”手法
撰稿 | 多客 来源 | 贝多财经 民营银行的诞生顺应了普惠金融的要求,承担着支持民营经济、服务小微的历史使命。经过近年来的发展,19家民营银行形成了特色化、差异化的发展模式,并用各自本领实践普惠金融的初心。 本文从多家民营银行在核心技…...

typescript中type、interface的区别
一、概念定义 interface:接口 在TS 中主要用于定义【对象类型】,可以对【对象】的形状进行描述。type :类型别名 为类型创建一个新名称,它并不是一个类型,只是一个别名。 二,区别 interface: …...

Ingress详解
Ingress Service对集群外暴露端口两种方式,这两种方式都有一定的缺点: NodePort :会占用集群集群端口,当集群服务变多时,缺点明显LoadBalancer:每个Service都需要一个LB,并且需要k8s之外设备支…...

【递归算法的Java实现及其应用】
文章目录 递归算法概述递归算法的实现步骤递归算法的Java实现递归算法的底层工作原理递归算法的底层代码讲解(优先级高)递归算法的实际应用场景递归算法在场景中解决的问题递归算法的优点和缺点总结 递归算法概述 递归算法是一种通过调用自身来解决问题…...
2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
目录 2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)1、A2、Bx3、Cut4、Diff5、EchoN6、Farmer7、GcdGame8、HouseSub9、IMissYou!10、Jargonless 2023年度第四届全国大学生算法设计与编程挑战赛(春季赛) 1、A 题目描述…...

如何用PHP获取各大电商平台的数据
PHP获取API数据是指使用PHP语言从web服务中提取数据。API是指应用程序接口,它允许应用程序之间进行交互和通信,并且允许一个应用程序从另一个应用程序获取数据。PHP是一种网站开发语言,它可以使用多种方式来获取API数据。 在PHP中࿰…...
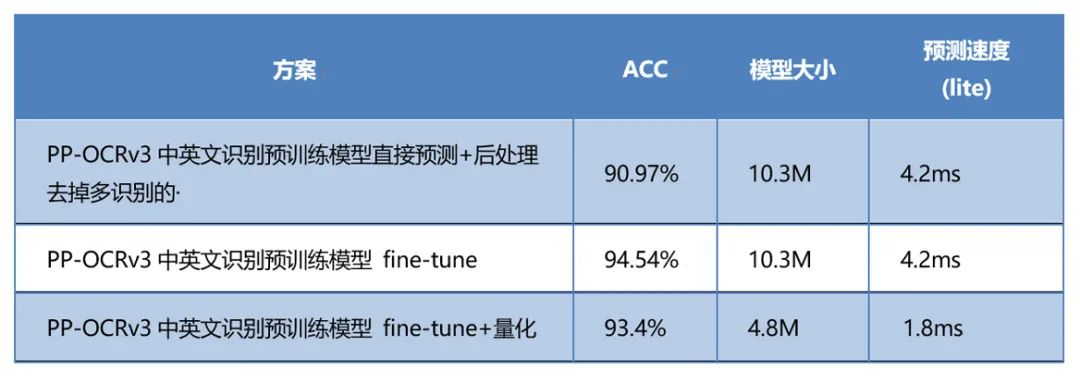
一站式完成车牌识别任务:从模型优化到端侧部署
交通领域的应用智能化不断往纵深发展,其中最为成熟的车牌识别早已融入人们的日常生活之中,在高速公路电子收费系统、停车场等场景中随处可见。一些企业在具体业务中倾向采用开源方案降低研发成本,但现有公开的方案中少有完成端到端的车牌应用…...
Linux4.8Nginx Rewrite
文章目录 计算机系统5G云计算第六章 LINUX Nginx Rewrite一、Nginx Rewrite 概述1.常用的Nginx 正则表达式2.rewrite和location3.location4.实际网站使用中,至少有三个匹配规则定义5.rewrite6.rewrite 示例 计算机系统 5G云计算 第六章 LINUX Nginx Rewrite 一、…...
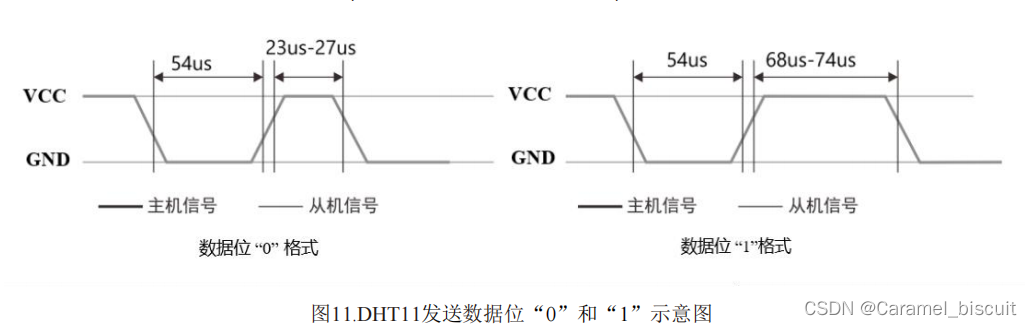
DHT11温湿度传感器
接口定义 传感器通信 DHT11采用简化的单总线通信。单总线仅有一根数据线(SDA),通信所进行的数据交换、挂在单总线上的所有设备之间进行信号交换与传递均在一条通讯线上实现。 单总线上必须有一个上拉电阻(Rp)以实现单…...

RestTemplate超简单上手
目录 1.什么是RestTemplate? 2.RestTemplate的使用 2.1spring环境下 注意1:RestTemplate中发送请求execute()和exchange()方法的区别 execute()方式 exchange()方式 二者的区别 注意2:进阶配置——底层HTTP客户端 2.2非spring环境下 1.什么是R…...

监控系统设计原则及实现目标
1.1.1.1 1 .完善的设计理念: 包括符合国际发展潮流的特性化设计,完整的安防监控及围墙周界报警系统 的布线、设备安装、调试、测试、验收的“交钥匙”工程管理制度,以及符合标 准的质量控制体系。 1.1.1.2 设计原则…...

VulnHub项目:MONEYHEIST: CATCH US IF YOU CAN
靶机名称: MONEYHEIST: CATCH US IF YOU CAN 地址:MoneyHeist: Catch Us If You Can ~ VulnHub 这个系列是一部剧改编,还是挺好看的,大家有兴趣可以去看看! 废话不多说,直接上图开始! 渗透…...

对象存储OSS简介,一分钟了解对象存储OSS
对象存储(Object Storage)是一种新兴的数据存储方式,与传统的文件系统和块存储不同,对象存储以对象为基本单位进行数据管理和存储。在对象存储中,每个对象都有唯一的标识符,并包含了数据本身以及与之相关的…...

SpringCloud_微服务基础day2(Eureka简介与依赖导入,服务注册与发现)
p6:Eureka简介与依赖导入 前面我们了解了如何对单体应用进行拆分,并且也学习了如何进行服务之间的相互调用,但是存在一个问题,就是虽然服务拆分完成,但是没有一个比较合理的管理机制,如果单纯只是这样编写,…...

#tmux# #终端# 常用工具tmux
tmux tmux是一个终端复用工具,允许用户在一个终端会话中同时管理多个终端窗口,提高了终端使用效率,尤其在服务器上进行远程管理时更加实用。在tmux中,可以创建多个终端窗口和窗格,并在这些窗口和窗格之间自由切换&…...

后端服务架构高性能设计之道
“N 高 N 可”,高性能、高并发、高可用、高可靠、可扩展、可维护、可用性等是后台开发耳熟能详的词了,它们中有些词在大部分情况下表达相近意思。本序列文章旨在探讨和总结后台架构设计中常用的技术和方法,并归纳成一套方法论。 前言 本文主…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
