Python 中的 F-Test
文章目录
- F 统计量和 P 值
- 方差(ANOVA) 分析中的 F 值
本篇文章介绍 F 统计、F 分布以及如何使用 Python 对数据执行 F-Test 测试。
F 统计量是在方差分析检验或回归分析后获得的数字,以确定两个总体的平均值是否存在显着差异。 它类似于 T 检验的 T 统计量,执行 T 检验会告诉您单个变量是否具有统计显着性,而 F 检验会告诉您一组变量是否具有统计显着性。
统计显着性意味着什么?
如果你有一个实质性的结果,那么你得到这些结果可能不是巧合。 如果您的检验结果在统计上不显着,则必须丢弃它们,因为它们无效,并且您不能拒绝原假设。
F 统计量和 P 值
在确定总体结果是否显着时,您必须考虑 F 统计量和 p 值。
为什么? 结果显着并不一定意味着您的所有变量也都显着。 简而言之,统计涉及比较所有变量的综合影响。
方差(ANOVA) 分析中的 F 值
方差分析检验是一种统计分析方法,用于评估基于方差的均值差异,以查看两个或多个分类组之间是否存在统计上重要的差异。
ANOVA 将自变量分成两组或更多组,这是另一个重要的组成部分。 例如,一个或多个组可能被预测会影响因变量,而另一组可能被用作控制组并且预计不会产生影响。
在某种程度上,在方差分析中,F 值就像一种工具,有助于回答两个统计量或总体的均值之间的方差是否显着不同的问题。 P 值是获得至少与观察到的结果一样极端的结果的可能性,假定零假设为真,同样由方差分析中的 F 值确定。
称为 f 比率的测试统计量可以计算如下:
要使用 Python 执行以下测试,我们可以使用 Python 中的 SciPy 模块。
SciPy 为许多问题类型提供算法,包括优化、积分、插值、特征值问题、代数方程、微分方程、统计等等。
要安装 scipy,请运行以下命令:
pip install scipy
我们可以在 scipy.stats 模块中使用以下类。 scipy 中的 stats 类包含执行统计操作所需的所有函数和类。
>>> from scipy.stats import f
scipy.stats.f 有一个 CDF(累积分布函数)方法。 可以针对给定的统计信息计算使用 p 值。
因此,您可以确定是拒绝还是接受给定 alpha 水平的 NULL 假设。
考虑下面的例子:
导入模块并创建变量。
from scipy.stats import f
import numpy as np
a = np.array([1,2,1,2,1,2,1,2,1,2])
b = np.array([1,3,-1,2,1,5,-1,6,-1,2])
alpha = 0.05 # you can set to level.
The formula to calculate the F value is Var(X)/Var(Y).# calculating F value.
F = a.var()/b.var()
Since F is a distribution:df1 = len(a) - 1
df2 = len(b) - 1
scipy.stats.f 类包含我们可以用来计算给定统计数据的 p 值和临界值的函数。
# Fetching p-value.
p_value = f.cdf(F, df1, df2)
p_value > alpha
从上面的代码中,我们可以得到使用F统计计算的p值; 我们将拒绝 NULL 假设,即 a 的方差等于 b 的方差。
假设您对所提供的反映正态性的数据没有信心。 F 检验的更可靠替代方法是 Bartlett 检验或 Levene 检验。
Scipy 还提供了执行这些测试的工具。
巴特利特测试:
>>> from scipy.stats import bartlett
>>> x = [8.88, 9.12, 9.04, 8.98, 9.00, 9.08, 9.01, 8.85, 9.06, 8.99]
>>> y = [8.88, 8.95, 9.29, 9.44, 9.15, 9.58, 8.36, 9.18, 8.67, 9.05]
>>> z = [8.95, 9.12, 8.95, 8.85, 9.03, 8.84, 9.07, 8.98, 8.86, 8.98]
>>> stat, p = bartlett(x, y, z)
>>> p
1.1254782518834628e-05
p 值非常小; 我们可以说给定的总体没有相等的方差。
这是因为方差的不同。
>>> [np.var(x, ddof=1) for x in [x, y, z]]
[0.007054444444444413, 0.13073888888888888, 0.008890000000000002]
Levene 的测试:
>>> from scipy.stats import levene
>>> x = [8.88, 9.12, 9.04, 8.98, 9.00, 9.08, 9.01, 8.85, 9.06, 8.99]
>>> y = [8.88, 8.95, 9.29, 9.44, 9.15, 9.58, 8.36, 9.18, 8.67, 9.05]
>>> z = [8.95, 9.12, 8.95, 8.85, 9.03, 8.84, 9.07, 8.98, 8.86, 8.98]
>>> stat, p = levene(x, y, z)
>>> p
0.002431505967249681
p 值非常小; 我们可以说给定的总体没有相等的方差。
>>> [np.var(x, ddof=1) for x in [x, y, z]]
[0.007054444444444413, 0.13073888888888888, 0.008890000000000002]
相关文章:

Python 中的 F-Test
文章目录 F 统计量和 P 值方差(ANOVA) 分析中的 F 值 本篇文章介绍 F 统计、F 分布以及如何使用 Python 对数据执行 F-Test 测试。 F 统计量是在方差分析检验或回归分析后获得的数字,以确定两个总体的平均值是否存在显着差异。 它类似于 T 检验的 T 统计量…...

Docker网络模式
一、docker网络概述 1、docker网络实现的原理 Docker使用Linux桥接,在宿主机虚拟一个Docker容器网桥(docker0),Docker启动一个容器时会根据Docker网桥的网段分配给容器一个IP地址,称为Container-IP, 同时Docker网桥是 每个容器的…...

百度离线资源治理
作者 | 百度MEG离线优化团队 导读 近些年移动互联网的高速发展驱动了数据爆发式的增长,各大公司之间都在通过竞争获得更大的增长空间,大数据计算的效果直接影响到公司的发展,而这背后其实依赖庞大的算力及数据作为支撑,因此在满足…...
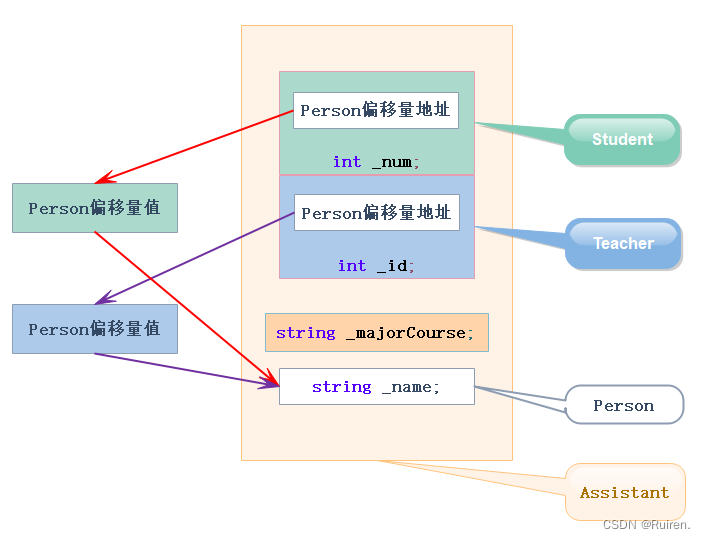
C++进阶之继承
文章目录 前言一、继承的概念及定义1.继承概念2.继承格式与访问限定符3.继承基类与派生类的访问关系变化4.总结 二、基类和派生类对象赋值转换基本概念与规则 三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员六、复杂的菱形继承及菱形虚拟继承七、…...
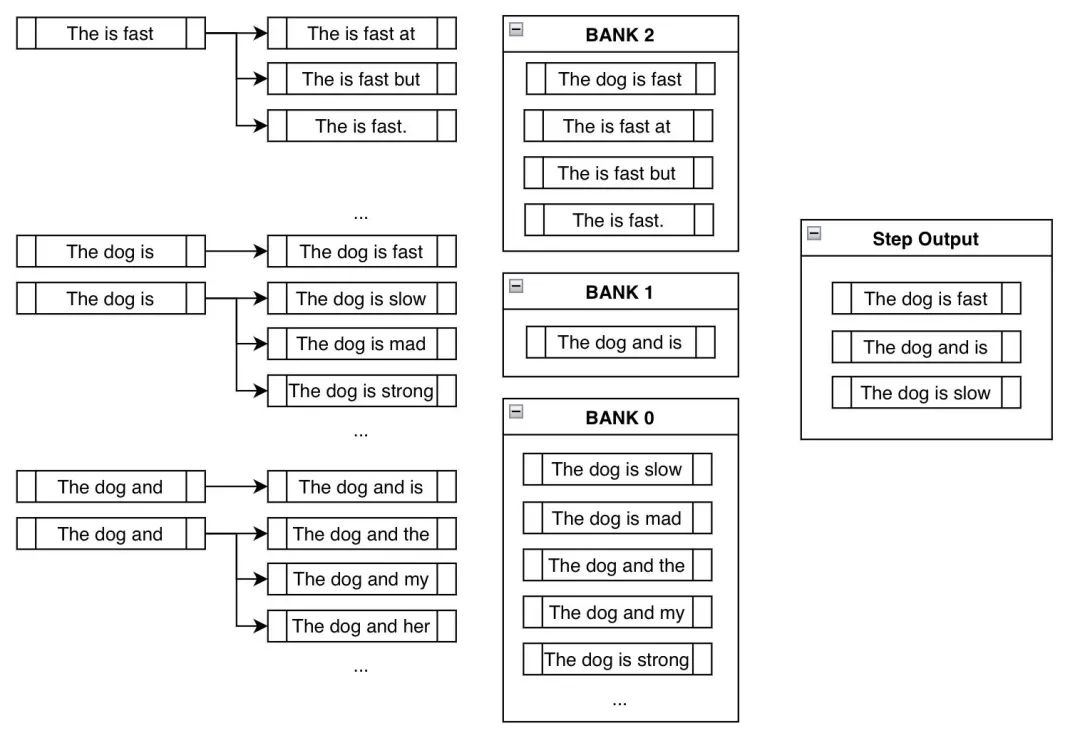
在 Transformers 中使用约束波束搜索引导文本生成
引言 本文假设读者已经熟悉文本生成领域波束搜索相关的背景知识,具体可参见博文 如何生成文本: 通过 Transformers 用不同的解码方法生成文本。 与普通的波束搜索不同,约束 波束搜索允许我们控制所生成的文本。这很有用,因为有时我们确切地知…...

Centos7更换OpenSSL版本
OpenSSL 1.1.0 用户应升级至 1.1.0aOpenSSL 1.0.2 用户应升级至 1.0.2iOpenSSL 1.0.1 用户应升级至 1.0.1u 查看openssl版本 openssl version -v选择升级版本 我的版本是OpenSSL 1.0.2系列,所以要升级1.0.2i https://www.openssl.org/source/old/1.0.2/openssl-…...
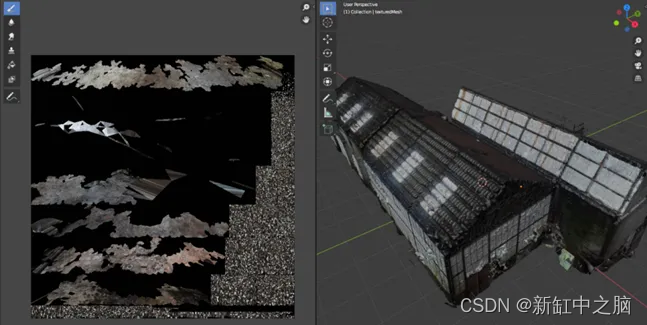
基于摄影测量的三维重建【终极指南】
我们生活的时代非常令人兴奋,如果你对 3D 东西感兴趣,更是如此。 我们有能力使用任何相机,从感兴趣的物体中捕捉一些图像数据,并在眨眼间将它们变成 3D 资产! 这种通过简单的数据采集阶段进行的 3D 重建过程是许多行业…...

配置ThreadPoolExecutor
ThreadPoolExecutor为一些Executor 提供了基本的实现,这些Executor 是由Executors中的newCachedThreadPool、newFixedThreadPool和newScheduledThreadExecutor 等工厂方法返回的。ThreadPoolExecutor是一个灵活的、稳定的线程池,允许进行各种定制。 如果默认的执行策略不能满足…...
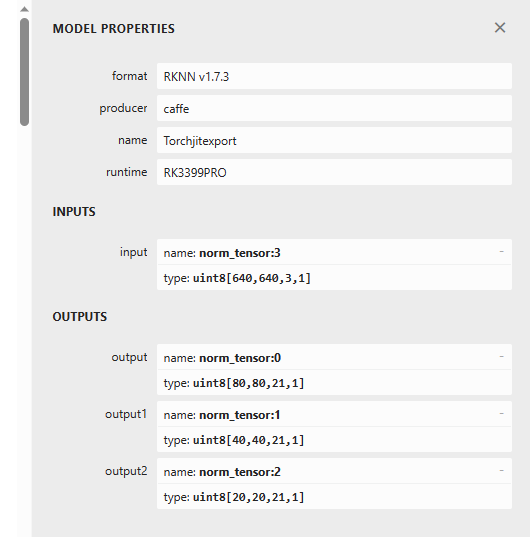
Yolov5s算法从训练到部署
文章目录 PyTorch GPU环境搭建查看显卡CUDA版本Anaconda安装PyTorch环境安装PyCharm中验证 训练算法模型克隆Yolov5代码工程制作数据集划分训练集、验证集修改工程相关文件配置预训练权重文件配置数据文件配置模型文件配置 超参数配置 测试训练出来的算法模型 量化转换算法模型…...
分布式补充技术 01.AOP技术
01.AOP技术是对于面向对象编程(OOP)的补充。是按照OCP原则进行的编写,(ocp是修改模块权限不行,扩充可以) 02.写一个例子: 创建一个新的java项目,在main主启动类中,写如下代码。 package com.co…...
)
QT 多对一服务插件 CTK开发(五)
CTK在软件的开发过程中可以很好的降低复杂性、使用 CTK Plugin Framework 提供统一的框架来进行开发增加了复用性 将同一功能打包可以提供多个应用程序使用避免重复性工作、可以进行版本控制提供了良好的版本更新迭代需求、并且支持动态热拔插 动态更新、开发更加简单快捷 方便…...

[Windows]_[初级]_[创建目录和文件的名字注意事项]
场景 在开发Windows程序时,会出现目录生成了,但是函数无法在目录里创建文件,怎么回事?说明 在之前说过Windows上有些字符是不能作为文件名的[1],但是检查了下出问题的目录名没有非法字符,所以不是这个原因。 把文件的绝对路径打印出来就发现了问题,目录名后边带了空格,…...

「QT」QT5程序设计目录
✨博客主页:何曾参静谧的博客 📌文章专栏:「QT」QT5程序设计 目录 📑【QT的基础知识篇】📑【QT的GUI编程篇】📑【QT的项目示例篇】📑【QT的网络编程篇】📑【QT的数据库编程篇】📑【QT的跨平台编程篇】📑【QT的高级编程篇】📑【QT的开发工具篇】📑【QT的调…...

ConcurrentHashMap核心源码(JDK1.8)
一、ConcurrentHashMap的前置知识扫盲 ConcurrentHashMap的存储结构? 数组 链表 红黑树 二、ConcurrentHashMap的DCL操作 HashMap线程不安全,在并发情况下,或者多个线程同时操作时,肯定要使用ConcurrentHashMap 无论是HashM…...

【Python】文件 读取 写 os模块 shutil模块 pickle模块
目录 1.文件 1.1 读取操作 1.2 写操作 1.3 os:文件管理 1.4 os.path:获取文件属性 1.5 shutil:文件的拷贝删除移动解压缩 1.6 pickle:数据永久存储 1.文件 文件编码 编码是一种规则集合,记录内容和二进制间相互…...

PAT A1087 All Roads Lead to Rome
1087 All Roads Lead to Rome 分数 30 作者 CHEN, Yue 单位 浙江大学 Indeed there are many different tourist routes from our city to Rome. You are supposed to find your clients the route with the least cost while gaining the most happiness. Input Specific…...

浅谈HttpURLConnection所有方法详解
HttpURLConnection 类是 Java 中用于实现 HTTP 协议的基础类,它提供了一系列方法来建立与 HTTP 服务器的连接、发送请求并读取响应信息。下面是 HttpURLConnection 类中常用的方法以及其详细解释: ---------------------------------------------------…...

前端快速创建web3应用模版分享
一、起因 一直以来都有一个创建前端Dapp模版的愿望,一来是工作中也有这样的需要,避免每次都要抽离重复的代码。二来是这样的模版也能帮助其他前端快速了解到web3应用的脚手架以及框架结构。于是决定整理一个模版并开源,希望我的代码能帮助到大…...

越权漏洞讲解
越权漏洞是指系统或应用程序中存在的安全漏洞,允许攻击者以超越其授权范围的方式访问系统资源或执行特权操作。这种漏洞可能会导致严重的安全风险,因为攻击者可以利用它来获取敏感信息、修改系统设置或执行恶意操作。 下面是一些常见的越权漏洞类型和它…...
短视频矩阵源码系统打包.源码
Masayl是一款基于区块链技术的去中心化应用程序开发平台,可帮助开发者快速、便捷地创建去中心化应用程序。Masayl拥有丰富的API和SDK,为开发者们提供了支持。此外,Masayl还采用了高效的智能合约技术,确保应用程序的稳定、安全和高…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
