【运筹优化】最短路算法之SPFA算法 + Java代码实现
文章目录
- 一、SPFA算法简介
- 二、SPFA算法思想
- 三、Java代码实现
- 四、测试
一、SPFA算法简介
SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同,为 O(VE)。
SPFA算法的全称是:Shortest Path Faster Algorithm,是西南交通大学段凡丁于 1994 年发表的论文中的名字。不过,段凡丁的证明是错误的,且在 Bellman-Ford 算法提出后不久(1957 年)已有队列优化内容,所以国际上不承认 SPFA 算法是段凡丁提出的。
二、SPFA算法思想
若给定的图存在负权边,类似Dijkstra算法等算法便没有了用武之地,SPFA算法便派上用场了。简洁起见,我们约定加权有向图G不存在负权回路,即最短路径一定存在。
用数组d记录每个结点的最短路径估计值,而且用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
定理
只要最短路径存在,上述SPFA算法必定能求出最小值。证明:每次将点放入队尾,都是经过松弛操作达到的。换言之,每次的优化将会有某个点v的最短路径估计值d[v]变小。所以算法的执行会使d越来越小。由于我们假定图中不存在负权回路,所以每个结点都有最短路径值。因此,算法不会无限执行下去,随着d值的逐渐变小,直到到达最短路径值时,算法结束,这时的最短路径估计值就是对应结点的最短路径值。
实际上,如果一个点进入队列达到n次,则表明图中存在负环,没有最短路径。
段凡丁论文中的复杂度证明 (O(kE),k 是小常数)是错误的,在此略去。该算法的最坏复杂度为 O(VE)。
对SPFA的一个很直观的理解就是由无权图的BFS转化而来。在无权图中,BFS首先到达的顶点所经历的路径一定是最短路(也就是经过的最少顶点数),所以此时利用数组记录节点访问可以使每个顶点只进队一次,但在带权图中,最先到达的顶点所计算出来的路径不一定是最短路。一个解决方法是放弃数组,此时所需时间自然就是指数级的,所以我们不能放弃数组,而是在处理一个已经在队列中且当前所得的路径比原来更好的顶点时,直接更新最优解。
SPFA算法有两个优化策略SLF和LLL
SLF:Small Label First 策略,设要加入的节点是j,队首元素为i,若dist(j)<dist(i),则将j插入队首,否则插入队尾;
LLL:Large Label Last 策略,设队首元素为i,队列中所有dist值的平均值为x,若dist(i)>x则将i插入到队尾,查找下一元素,直到找到某一i使得dist(i)<=x,则将i出队进行松弛操作。SLF 和 LLF 在随机数据上表现优秀,但是在正权图上最坏情况为 O(VE),在负权图上最坏情况为达到指数级复杂度。
三、Java代码实现
@Data
public class SPFA {// 距离矩阵double[][] distance;// 起点int start;// 终点int end;/*** @param distance* @param start* @param end* @Description 构造函数* @Author WSKH*/public SPFA(double[][] distance, int start, int end) {this.distance = distance;this.start = start;this.end = end;}/*** @Description 进行求解* @Author WSKH*/public void solve() {// 初始化dis一维数组double[] dis = new double[distance.length];for (int i = 0; i < dis.length; i++) {if (i != start) {dis[i] = Double.MAX_VALUE;}}// 声明队列(用集合模拟)List<Integer> list = new LinkedList<>();// 初始化队列,添加起点进入队列list.add(start);// 记录每个顶点入队的次数int[] counter = new int[distance.length];counter[start]++;//HashMap<Integer,List<Integer>> shortestPathMap = new HashMap<>();for (int i = 0; i < distance.length; i++) {List<Integer> arrayList = new ArrayList<>();arrayList.add(start);shortestPathMap.put(i,arrayList);}// 开始循环while (!list.isEmpty()) {// 获取当前队首元素索引int index = list.remove(0);// 看看能不能松弛for (int i = 0; i < dis.length; i++) {if (i != start && i != index && dis[i] > distance[index][i] + dis[index]) {dis[i] = distance[index][i] + dis[index];List<Integer> integerList = new ArrayList<>(shortestPathMap.get(index));integerList.add(i);shortestPathMap.put(i,integerList);// 看看i能不能入队if (!list.contains(i)) {list.add(i);counter[i]++;// 如果某个顶点入队次数大于顶点数,那么说明图中存在负权回路if (counter[i] > distance.length) {throw new RuntimeException("存在负权回路!" + Arrays.toString(counter));}}}}}System.out.println("每个顶点入队次数为:" + Arrays.toString(counter));System.out.println("起点到其余各个点的最短路为:" + Arrays.toString(dis));System.out.println(shortestPathMap.get(end));}
}
四、测试
public class Test {public static void main(String[] args) {double[][] distance = new double[][]{{0, 8, 9, 2, 5},{8, 0, 7, 2, 8},{9, 7, 0, 3, 9},{2, 2, 3, 0, 5},{5, 8, 9, 5, 0},};new SPFA(distance,0,2).solve();}
}
控制台输出:
每个顶点入队次数为:[1, 2, 2, 1, 1]
起点到其余各个点的最短路为:[0.0, 4.0, 5.0, 2.0, 5.0]
[0, 3, 2]
其中 [0, 3, 2] 代表0到2的最短路径为:0->3->2
相关文章:

【运筹优化】最短路算法之SPFA算法 + Java代码实现
文章目录 一、SPFA算法简介二、SPFA算法思想三、Java代码实现四、测试 一、SPFA算法简介 SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同…...
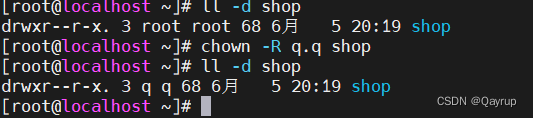
linuxOPS基础_linux权限管理
权限概述 什么是权限 在多用户计算机系统的管理中,权限是指某个特定的用户具有特定的系统资源使用权利。 在Linux 中分别有读、写、执行权限 \权限针对文件权限针对目录读r(read)表示可以查看文件内容;cat、less…表示可以(ls)查看目录中存在的文…...
linux安装homeassistant(智能设备远程控制开源框架)
1、安装docker 先切换到root 用户,先安装一些基本环境: yum install -y yum-utils device-mapper-persistent-data lvm2添加阿里云软件源 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo然后安装 D…...

TensorRT Triton Inference Server: 版本 error魔术标记不匹配 , NGC使用
魔术标记不匹配错误Serialization assertion magicTagRead kMAGIC_TAG failed.Magic tag does not match 原因: 转换和推理使用的镜像的标签是相同的,但是转换的镜像中pip list得到trt版本为8.6.0,但是推理环境中 rootf2c810ba3976:/# /usr/…...
)
Elasticsearch 文本分析器(下)
字符过滤器 注意:字符过滤器用于在将字符流传递给分词器之前对其进行预处理 html_strip HTML元素替换过滤器 此过滤器会替换掉HTML标签,且会转换HTML实体 如:& 会被替换为 &。 {"tokenizer": "keyword","…...

Git操作方法
目录 Git是什么 Git特点 Git作用 Git原理 集中式 分布式 Git安装 修改语言 Git操作 1.初始化Git仓库 2.提交工作区的内容到版本库 3.查看版本记录 4.版本回退 5.版本前进 Git 命令 通用操作 工作状态 版本回退 版本前进 远程仓 1.GitHub 2.GitLab 3.码云…...

CorelDRAW矢量绘图2023中文版下载
市面上的矢量绘图工具虽然很多,但权威又专业的却不多,选到不好用的工具,会极大的影响自己创作,CorelDRAW简称cdr,是一款功能强大的矢量图制作软件,一说到矢量图制作,大家都会不由自主地想到cdr。…...

Java-API简析_java.lang.Float类(基于 Latest JDK)(浅析源码)
【版权声明】未经博主同意,谢绝转载!(请尊重原创,博主保留追究权) https://blog.csdn.net/m0_69908381/article/details/131129886 出自【进步*于辰的博客】 其实我的【Java-API】专栏内的博文对大家来说意义是不大的。…...
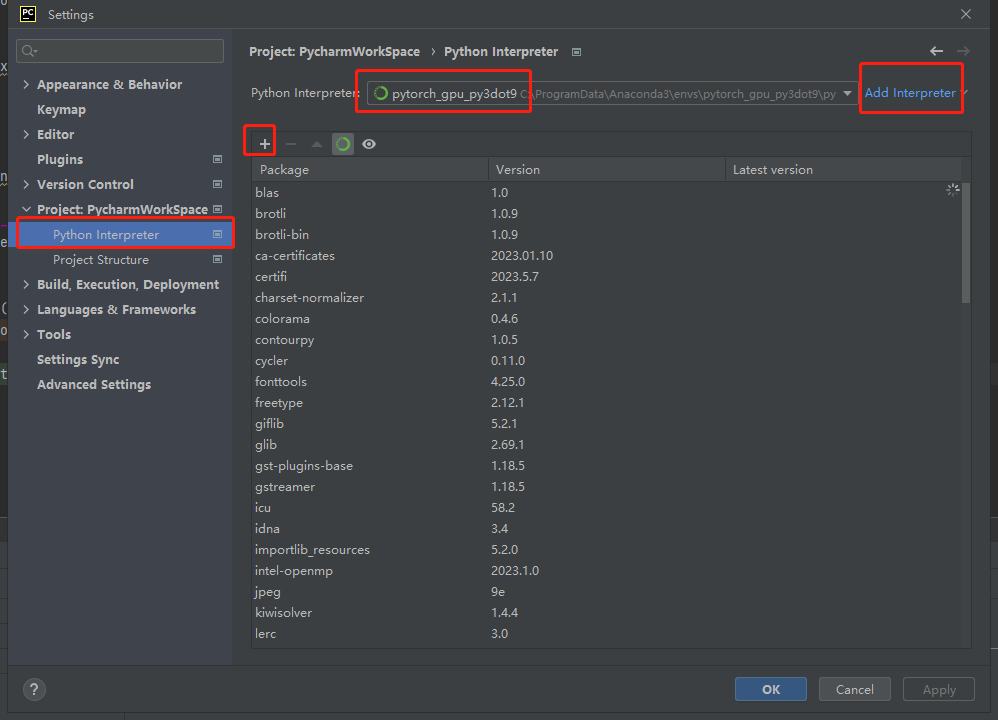
pycharm的基本使用
废话文学 本人记录笔记始终遵循“能动手绝不动脑,能动脑绝不动手”的基本原则。不会的操作,跟着笔记干就完事了,还动啥脑袋?留着脑细胞刷抖音擦边小姐姐他不香吗? 什么是IDE IDE即【集成开发环境】,Inte…...
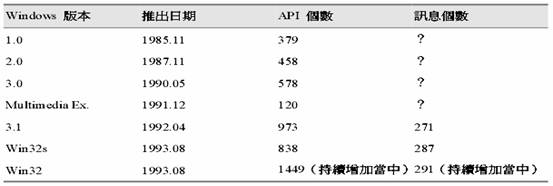
为什么要使用微软的 Application Framework?
我是荔园微风,作为一名在IT界整整25年的老兵,今天来看一下我们为什么要使用微软的 Application Framework? 虽然Application Framework 并不是新观念,它们却在最近数年才成为 PC 平台上软件开发的主流工具。面向对象语言是具体实…...

Python爬虫基础知识点
Python爬虫是使用Python编写的程序,可以自动抓取互联网上的数据。常用的Python爬虫框架包括Scrapy、BeautifulSoup、Requests等。Python爬虫可以应用于众多场合,如大数据分析、信息监测、数据挖掘和机器学习等领域。那么新手应该如何学习python爬虫呢&am…...

K8s运维备忘
1.服务器集群搭建: VagrantFile中加入以下代码,创建3个虚拟机: Vagrant.configure("2") do |config| (1..3).each do |i| config.vm.define "k8s-node#{i}" do |node| # 设置虚拟机的Box …...
)
激光雷达+rtk+rgb联合使用(4)
因为一直在忙一些乱七八糟的事情,就没顾得上继续写,想着快速收尾算了。 前面写到,我在点云的匹配上花了大量的时间,不断的调参数,换方法,一共几百个点云,想着先每50个匹配一次,得到几…...

【K8S系列】快速初始化⼀个最⼩集群
序言 走得最慢的人,只要不丧失目标,也比漫无目的地徘徊的人走得快。 文章标记颜色说明: 黄色:重要标题红色:用来标记结论绿色:用来标记一级重要蓝色:用来标记二级重要 希望这篇文章能让你不仅有…...
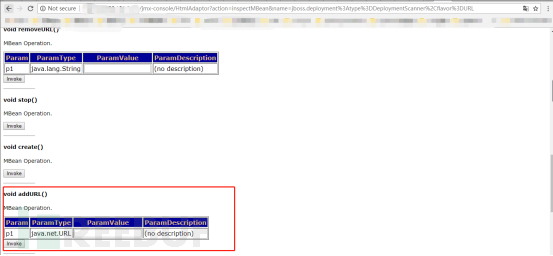
Exploit/CVE-2010-0738
打开JBoss的潘多拉魔盒:JBoss高危漏洞分析 *本文中涉及到的相关漏洞已报送厂商并得到修复,本文仅限技术研究与讨论,严禁用于非法用途,否则产生的一切后果自行承担。 前言 JBoss是一个基于J2EE的开放源代码应用服务器࿰…...
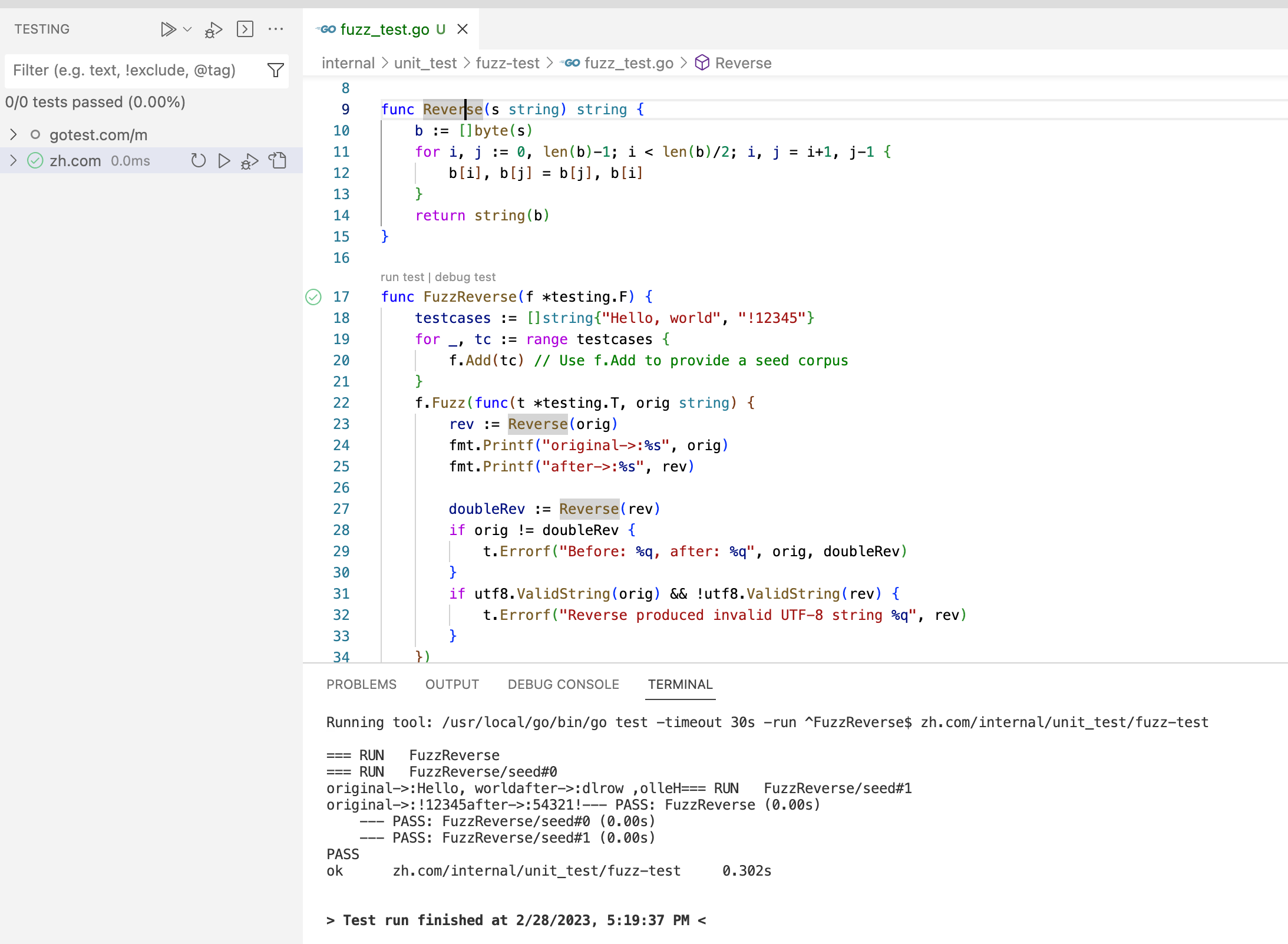
Go单元测试及框架使用
Go自带测试框架 单元测试 建议Go 语言推荐测试文件和源代码文件放在一块,测试文件以 _test.go 结尾。函数名必须以 Test 开头,后面一般跟待测试的函数名参数为 t *testing.T 简单测试用例定义如下: func TestXXXX(t *testing.T) {// ...}…...

TreeMap类型实体类数据进行排序
实体类Student类代码如下所示: package com.test.Test11;public class Student implements Comparable<Student>{private int age;private String name;private Double height;public int getAge() {return age;}public void setAge(int age) {this.age age…...
HOOPS助力AVEVA数字化转型:支持多种3D模型格式转换!
行业: 电力和公用事业、化工、造船、能源、采矿业 挑战: 创建大规模复杂资产的客户需要汇集多种类型的数据,以支持初始设计和创建强大的数字双胞胎;现有版本的产品只支持半打CAD格式;有限的内部开发资源限制了增加对新…...
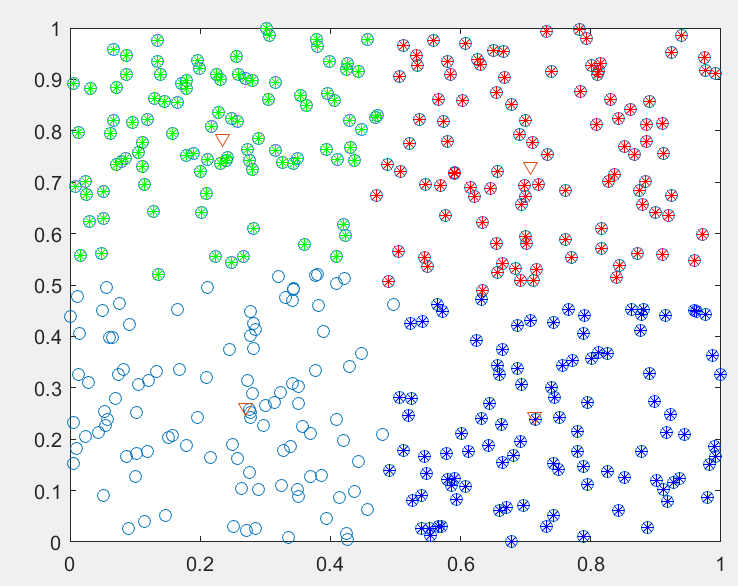
(转载)基于遗传模拟退火的聚类算法(matlab实现)
1 理论基础 1.1 模糊聚类分析 模糊聚类是目前知识发现以及模式识别等诸多领域中的重要研究分支之一。随着研究范围的拓展,不管是科学研究还是实际应用,都对聚类的结果从多方面提出了更高的要求。模糊C-均值聚类(FCM)是目前比较流行的一种聚类方法。该…...

【C++】struct 和 class 的区别
欢迎来到博主 Apeiron 的博客,祝您旅程愉快。时止则止,时行则行。动静不失其时,其道光明。 目录 1、缘起 2、示例代码 3、总结 1、缘起 在 C 中,struct 和 class 唯一的区别就在于 默认的访问权限不同。区别如下: …...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
