什么是 tokens,ChatGPT里面的Tokens如何计数?
什么是 tokens,ChatGPT里面的Tokens如何计数?
什么是 tokens?
Tokens 可以被认为是词语的片段。在 API 处理提示之前,输入会被分解成 tokens。这些 tokens 并不会精确地在单词的开始或结束处切分 - tokens 可以包含尾随的空格甚至子词。以下是一些帮助理解 tokens 长度的经验法则:
1 token ~= 英文中的4个字符
1 token ~= ¾个单词
100 tokens ~= 75个单词
或者
1-2个句子 ~= 30个tokens
1段落 ~= 100个tokens
1,500个单词 ~= 2048个tokens
为了获取更多关于tokens如何叠加的上下文,可以考虑以下例子:
- 韦恩·格雷茨基的名言 “You miss 100% of the shots you don’t take” 包含11个tokens。
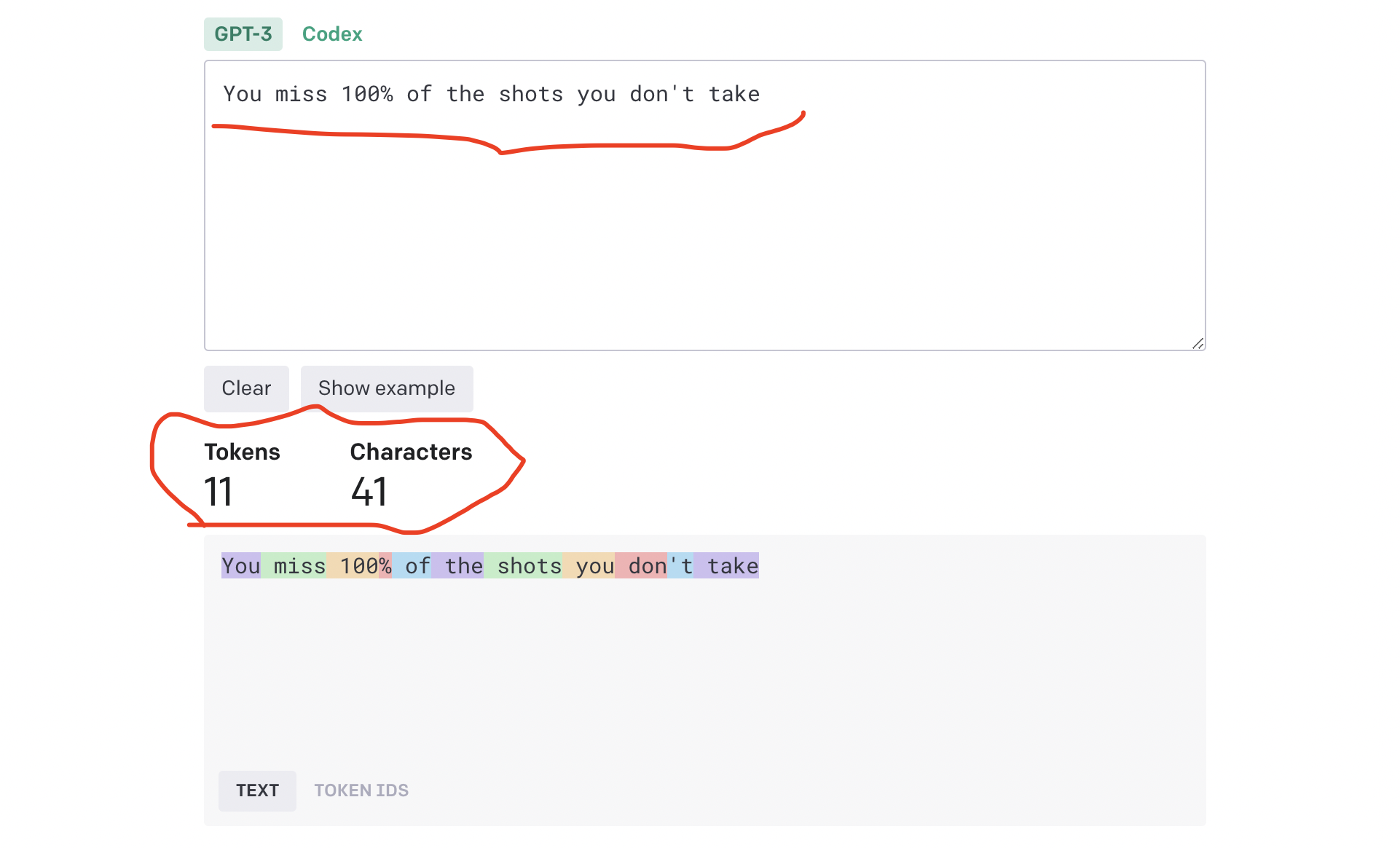
单词如何被分割成 tokens 也取决于语言。例如,‘Cómo estás’(西班牙语中的’你好吗’)包含5个 tokens(对应10个字符)。较高的 token 到字符比率可能使得对英语以外的语言实现 API 更加昂贵。

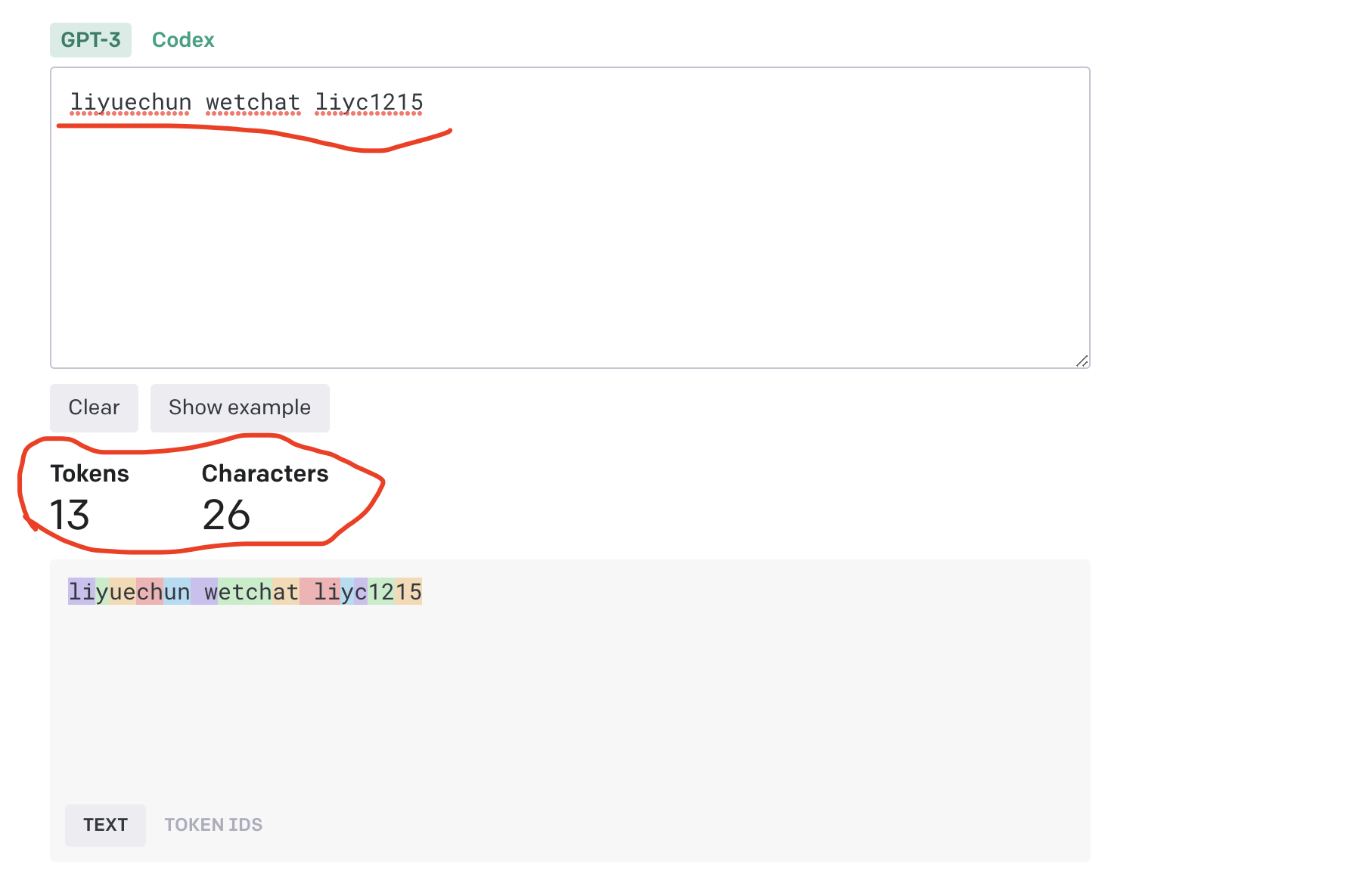
- 我名字拼音+空格+wetchat+我的微信号"liyuechun wetchat liyc1215" 包含13个tokens。
飞书、钉钉、企微GPT能力嫁接和AIGC企业培训,联系我:liyc1215
-
”黎跃春“三个字包含8个tokens

-
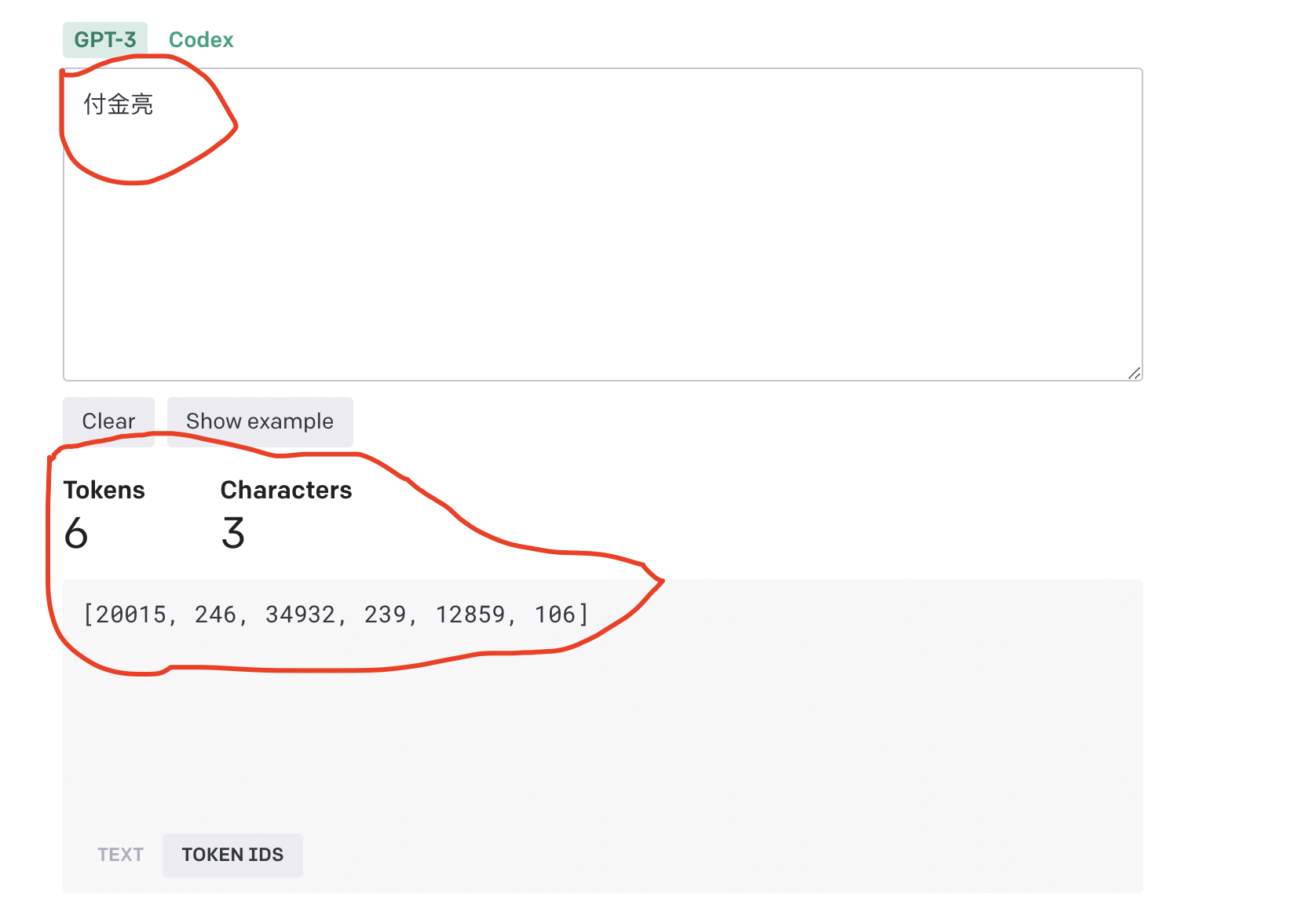
"付金亮"三个字包含6个tokens
如果你想进一步探索分词,你可以使用我们的交互式 Tokenizer 工具,它可以让你计算 token 的数量,并查看文本如何被分割成 tokens。或者,如果你想通过编程方式进行分词,可以使用 Tiktoken,这是一个专为 OpenAI 模型设计的快速 BPE 分词器。你也可以尝试探索其他库,例如 Python 的 transformers 包,或者 node.js 的 gpt-3-encoder 包。
Token 限制
根据使用的模型不同,请求中的prompt和completion之间最多可以使用4097个tokens。如果你的prompt是4000个tokens,那么你的completion最多可以是97个tokens。
这个限制目前是一个技术限制,但通常有许多创新的方法可以在这个限制内解决问题,例如压缩你的prompt,将文本分解成较小的部分等。
Token 定价
API 提供多种不同价格点的模型类型。每种模型都有一系列的能力,其中davinci是最强大的,ada是最快的。对这些不同模型的请求定价不同。你可以在这里找到关于token定价的详细信息。
探索 tokens
API会根据语料库数据中的上下文来处理单词。GPT-3接受prompt,将输入转换成一系列的tokens,处理prompt,并将预测的tokens转换回我们在响应中看到的单词。
在我们看来可能是两个相同的单词,可能会根据它们在文本中的结构生成不同的tokens。考虑一下API如何根据文本中的上下文为单词’red’生成token值:
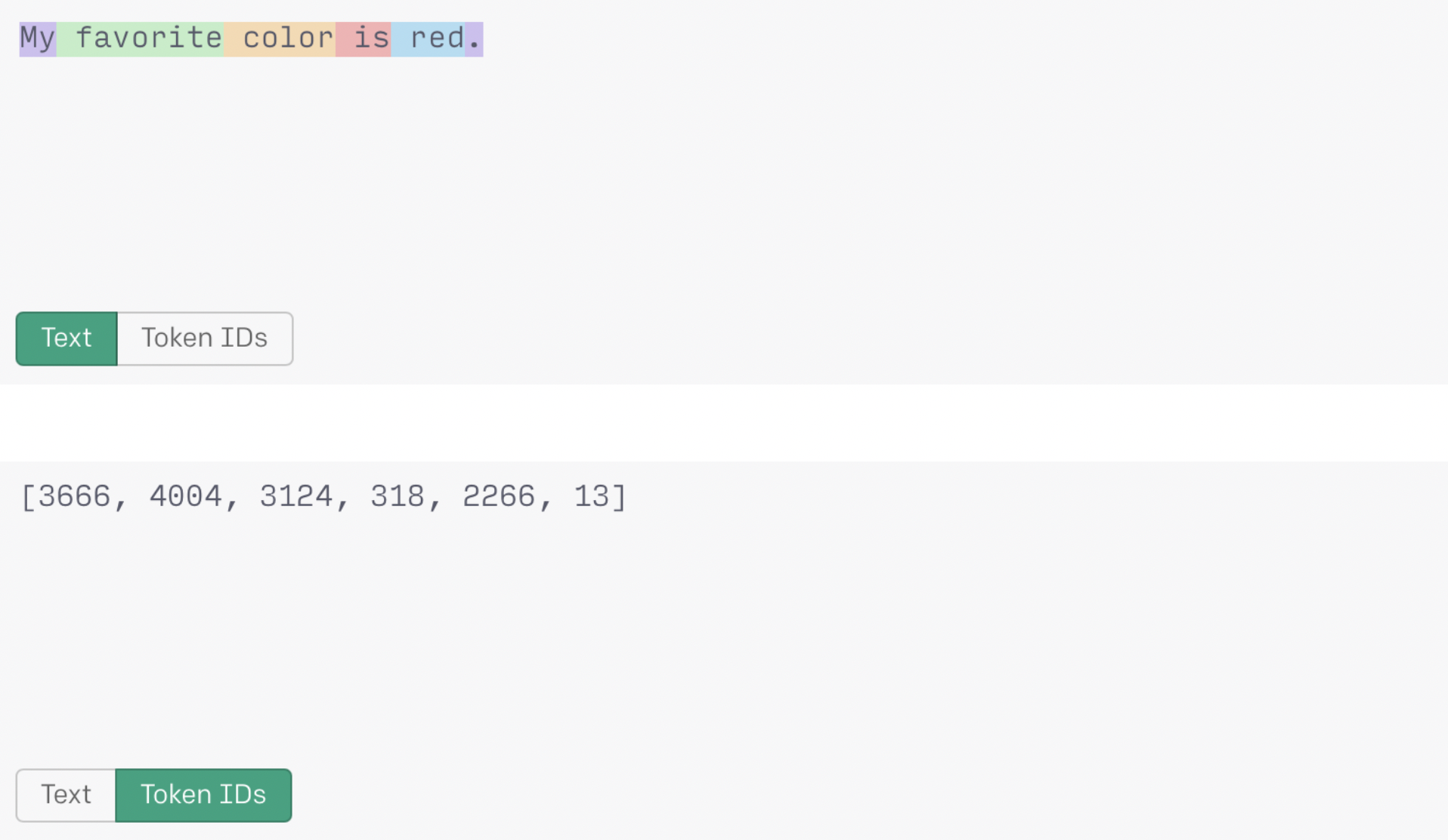
在上面的第一个例子中,‘ red’的token "2266"包含一个尾随的空格。
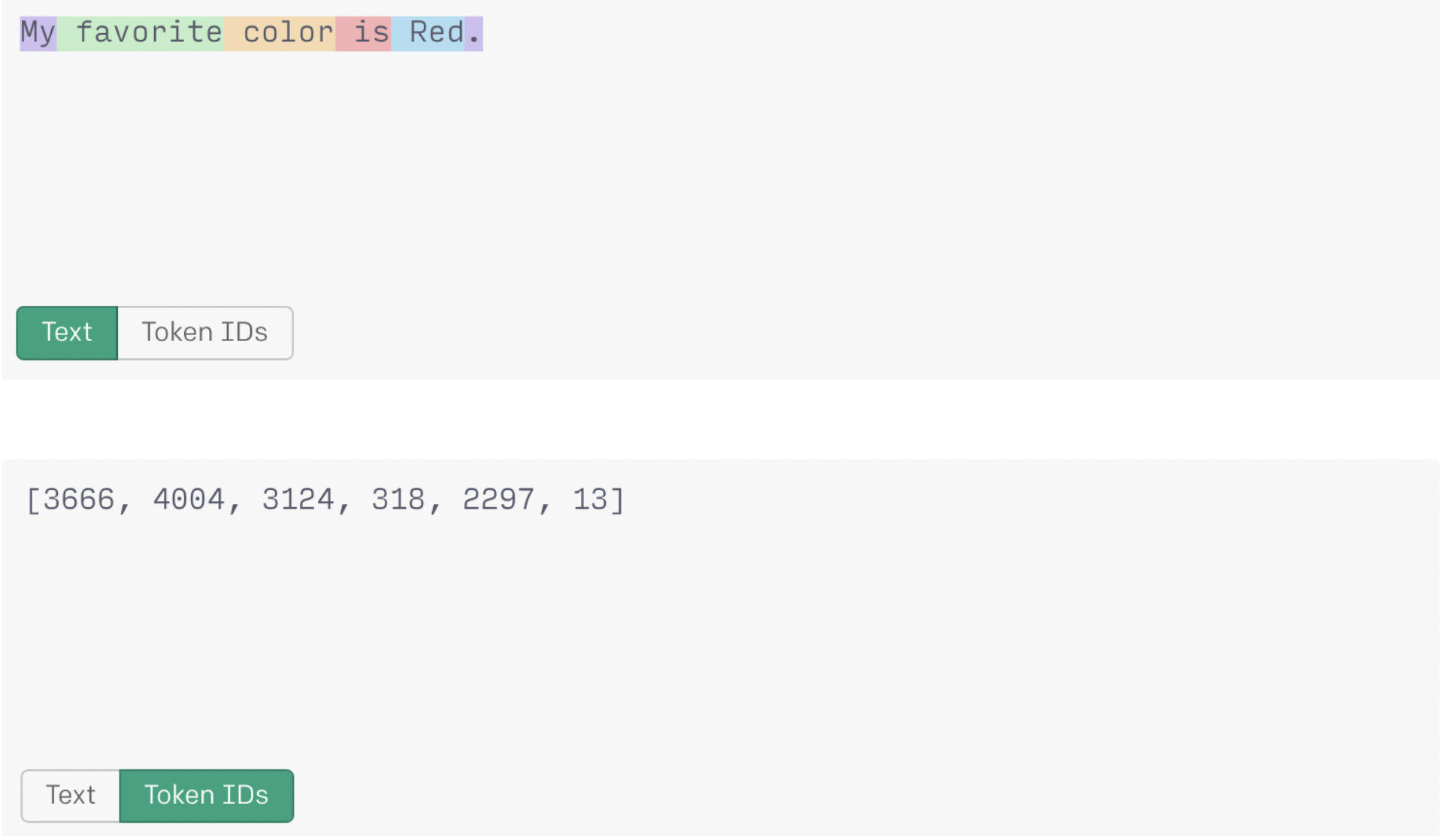
带有前导空格并以大写字母开头的‘ Red’的token "2297"与以小写字母开头的‘ red’的token "2266"不同。
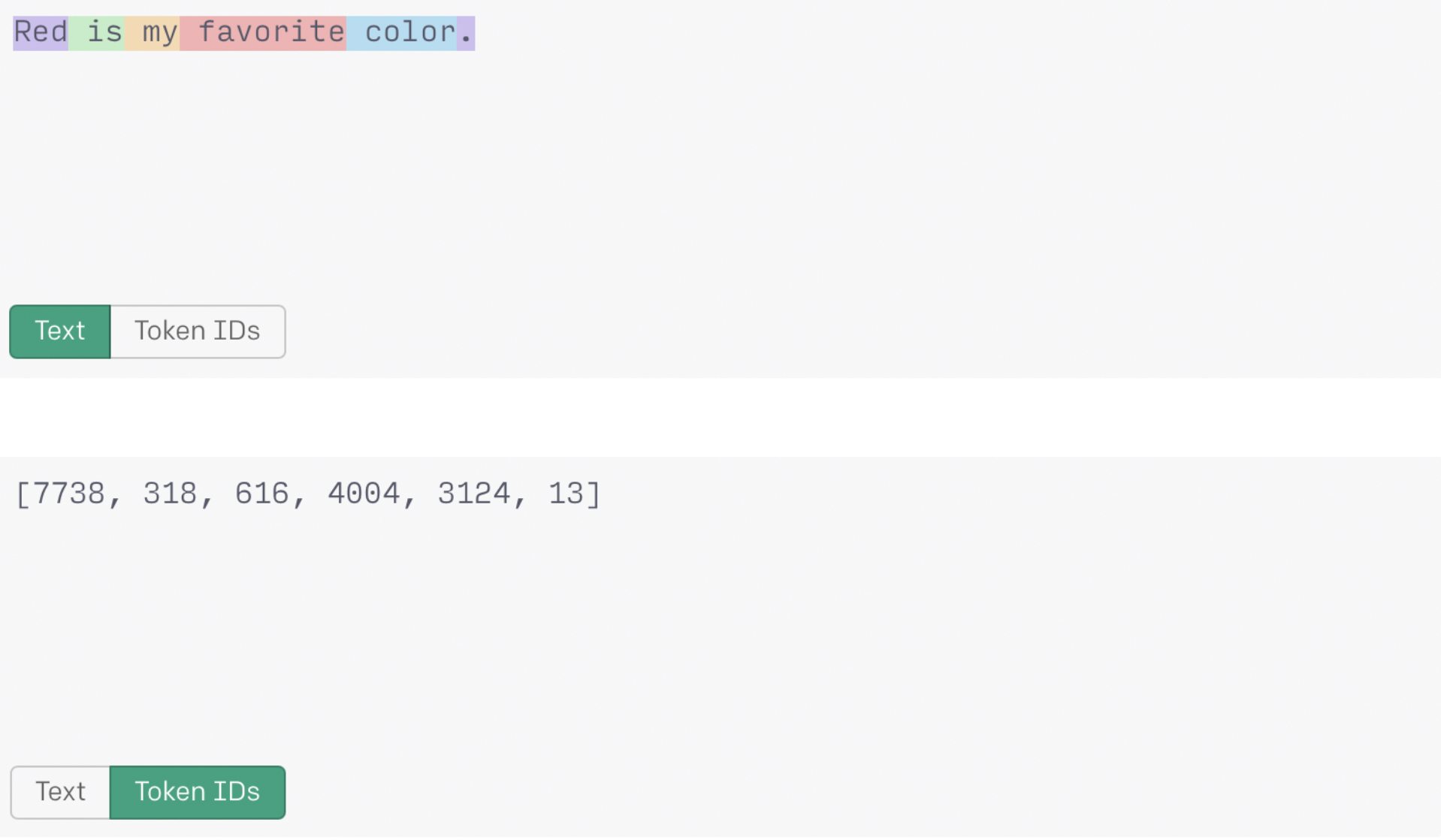
当 ‘Red’ 在句子开头时,生成的token不包含前导空格。token "7738"与前两个单词的例子不同。
观察:
token越可能/频繁,分配给它的token号就越低:
-
在所有3个句子中为句号生成的token是相同的(“13”)。这是因为,在语境上,句号在语料库数据中的使用相当类似。
-
根据’red’在句子中的位置,生成的token会有所不同:
-
在句子中间的小写:‘ red’ - (token: “2266”)
-
在句子中间的大写:‘ Red’ - (token: “2297”)
-
在句子开头的大写:‘Red’ - (token: “7738”)
-
既然我们知道tokens可以包含尾随的空格字符,那么记住以空格字符结束的prompts可能会导致输出质量较低是有帮助的。这是因为API已经在它的tokens字典中包含了尾随的空格。
使用 logit_bias 参数
可以在 logit_bias 参数中为特定的 tokens 设置偏差,以修改指定 tokens 出现在补全中的可能性。比如,我们正在构建一个对用户鸡蛋过敏问题敏感的 AI 烘焙助手。
当我们使用提示 ‘The ingredients for banana bread are’ 运行 API 时,回应将以26.8%的概率将 ‘eggs’ 包含为第二种原料。

注意:要在 Playground 中查看补全概率,请从 Show Probabilities 下拉菜单中选择 Full Spectrum。
由于我们的 AI 烘焙助手对鸡蛋过敏问题很敏感,我们可以利用我们对 tokens 的了解,在 logit_bias 参数中设置偏差,以阻止模型生成包含任何 ‘egg’ 变体的响应。
首先,使用这个分词器工具来确定我们需要为哪些 tokens 设置偏差。

Tokens:
-
尾随空格的单数形式:‘ egg’ - “5935”
-
尾随空格的复数形式:‘ eggs’ - “9653”
-
为‘Egg’或‘Eggs’生成的子词token - ‘gg’:“1130”
logit_bias 参数接受的偏差值范围是 -100 到 +100,极值结果导致相关 token 的禁止(-100)或独占选择(100)。
将 logit 偏差加到 prompt 中将修改 ‘egg’(及其变体)包含在我们的香蕉面包提示的响应中的可能性。上述提示生成了一个不包含任何鸡蛋的响应!
虽然我们不能保证它会生成最好的无鸡蛋香蕉面包配方,但 AI 烘焙助手满足了对用户鸡蛋过敏问题的考虑需求。
总结
- 使用英文对话比较划算,其他语言包括中文计算Token时比较昂贵
- 英文字母大概四个字母平均下来等于一个token
- 中文汉字,大概一个汉字平均下来两个token
- 我昨天用GPT写了7篇高考作文,总字数为
10397,Tokens 为21,008个。

计算了一下:如果使用GPT3.5的API访问的话,整个输入和输出总共:21,008 个token,GPT3.5 的单价为$0.002/1000tokens,那么这7篇作文的整个对话花费折算成人民币的价格为:21008/1000*(0.002*7) = 0.294112元人民币,GPT4是GPT3.5的60倍价格,如果使用GPT4的话,此次消费为:0.294112 * 60 = 17.64672元。
最后总结: 目前使用GPT3.5的价格还是很亲民划算的,等待未来算力足够的时候,我相信GPT4.0也不会贵。
原文链接:https://blog.yredu.xyz/archives/5119
相关文章:

什么是 tokens,ChatGPT里面的Tokens如何计数?
什么是 tokens,ChatGPT里面的Tokens如何计数? 什么是 tokens? Tokens 可以被认为是词语的片段。在 API 处理提示之前,输入会被分解成 tokens。这些 tokens 并不会精确地在单词的开始或结束处切分 - tokens 可以包含尾随的空格甚…...
工业镜头分类、相关参数含义
一、工业镜头参数 1、焦距/后焦距 焦距是像方主面到像方焦点的距离。后焦距指光线离开镜头最后一片镜片表面到sensor感光面的距离,如8mm,16mm,25mm等; 焦距的大小决定着视角大小,焦距数值小,视角大&#…...
)
码蹄杯语言基础:数组(C语言)
码蹄集网站地址:https://www.matiji.net/exam/ojquestionlist ⭐MT1381逆序输出数组 定义一个长度为10的整型数组,输入10个数组元素的值,然后逆序输出他们 格式 输入格式: 输入10个数组元素的值,整型,空…...

DJ4-2 程序的装入和链接
目录 4.2.1 程序的装入 一、绝对装入方式 二 、可重定位装入方式 三、动态运行时装入方式 4.2.2 程序的链接 一、静态链接 二、装入时动态链接 三、运行时动态链接 在多道程序环境下,如果程序要运行,那么必须为之创建进程。而创建进程的第一件…...

开源项目合集....
likeshop开源商城系统,公众号商城、H5商城、微信小程序商城、抖音小程序商城、字节小程序商城、头条小程序商城、安卓App商城、苹果App商城代码全开源,免费商用。 适用场景:B2C商城、新零售商城、社交电商商城、分销系统商城、小程序商城、商…...
机器学习 | 降维问题
目录 一、主成分分析 二、奇异值分解 2.1 奇异值分解原理 2.2 奇异值分解实践 三、特征值与特征向量 一、主成分分析 主成分有如下特征: 每个主成分是原变量的线性组合;各个主成分之间互不相关;主成分按照方差贡献率从大到小依次排列&…...
Ubuntu20.04平台下使用二进制包部署MongoDB-6.0.4单实例
文章目录 1.1 准备服务器的基本信息1.2 操作系统上创建其用户1.3 部署MongoDB服务端1.4 部署MongoDB客户端1.5 部署MongoDB 27017实例1.5.1 创建相关目录1.5.2 准备配置文件1.5.3 准备启停脚本1.5.4 进行启停测试1.5.5 加入开机自启动 1.6 创建超级管理员用户1.6.1 创建本地的超…...
Snipaste工具推荐
Snipaste Snipaste 不只是截图,善用贴图功能将帮助你提升工作效率! 新用户? 截图默认为 F1,贴图为 F3,然后请对照着 快捷键列表 按一遍,体会它们的用法,就入门啦! 遇到了麻烦&…...
MinIO快速入门——在Linux系统上安装和启动
1、简介 MinIO 是一款基于Go语言发开的高性能、分布式的对象存储系统。客户端支持Java,Net,Python,Javacript, Golang语言。MinIO系统,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。 2、环境搭建&#…...
07.JavaWeb-Vue+elementUI
1.Vue 功能替代JavaScript和jQuery,基于JavaScript实现的前端框架 1.1配置Vue 1.1.1引入vue库 方法一:通过cdn链接引入最新版本的vue(可能会慢些) <head><script src"https://cdn.jsdelivr.net/npm/vue">…...
经典面试题---【第一档】
1.如果你想new一个Quene,你有几种方式?他们之间的区别是什么? 2.Redis 是如何判断数据是否过期的呢? Redis 通过一个叫做过期字典(可以看作是 hash 表)来保存数据过期的时间。过期字典的键指向 Redis 数据…...

欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)正式启动,开启报名通道
6月8日,欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)启动仪式暨北京推介会圆满举行。活动由欧美同学会(中国留学人员联谊会)主办,中共浙江省委统战部支持,浙江省欧美同学会、中…...

python3 爬虫相关学习8:python 的常见报错内容 汇总收集
目录 1 拼写错误 AttributeError: NameError: 等等 2 类型错误 TypeError: 如字符串连接错误 TypeError: can only concatenate str (not “int“) to str 3 意外缩进 IndentationError: unexpected indent 4 找不到对应模块 ModuleNotFoundError: 5 语法错误 Syntax…...
活跃主机发现技术指南
活跃主机发现技术指南 1.活跃主机发现技术简介2.基于ARP协议的活跃主机发现技术3.基于ICMP协议的活跃主机发现技术4.基于TCP协议的活跃主机发现技术5.基于UDP协议的活跃主机发现技术6.基于SCTP协议的活跃主机发现技术7.主机发现技术的分析 1.活跃主机发现技术简介 在生活中有这…...
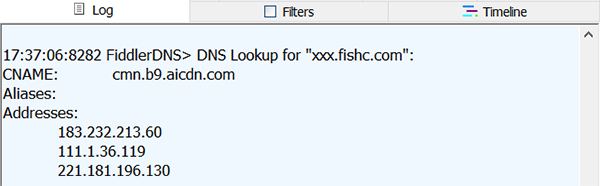
手机抓包fiddler配置及使用教程
本文基于Fiddler4讲解基本使用 fiddler抓包原理 注意:Fiddler 是以代理web服务器的形式工作的,它使用代理地址:127.0.0.1,端口:8888。当Fiddler退出的时候它会自动注销,这样就不会影响别的 程序。不过如果Fiddler非正常退出&…...
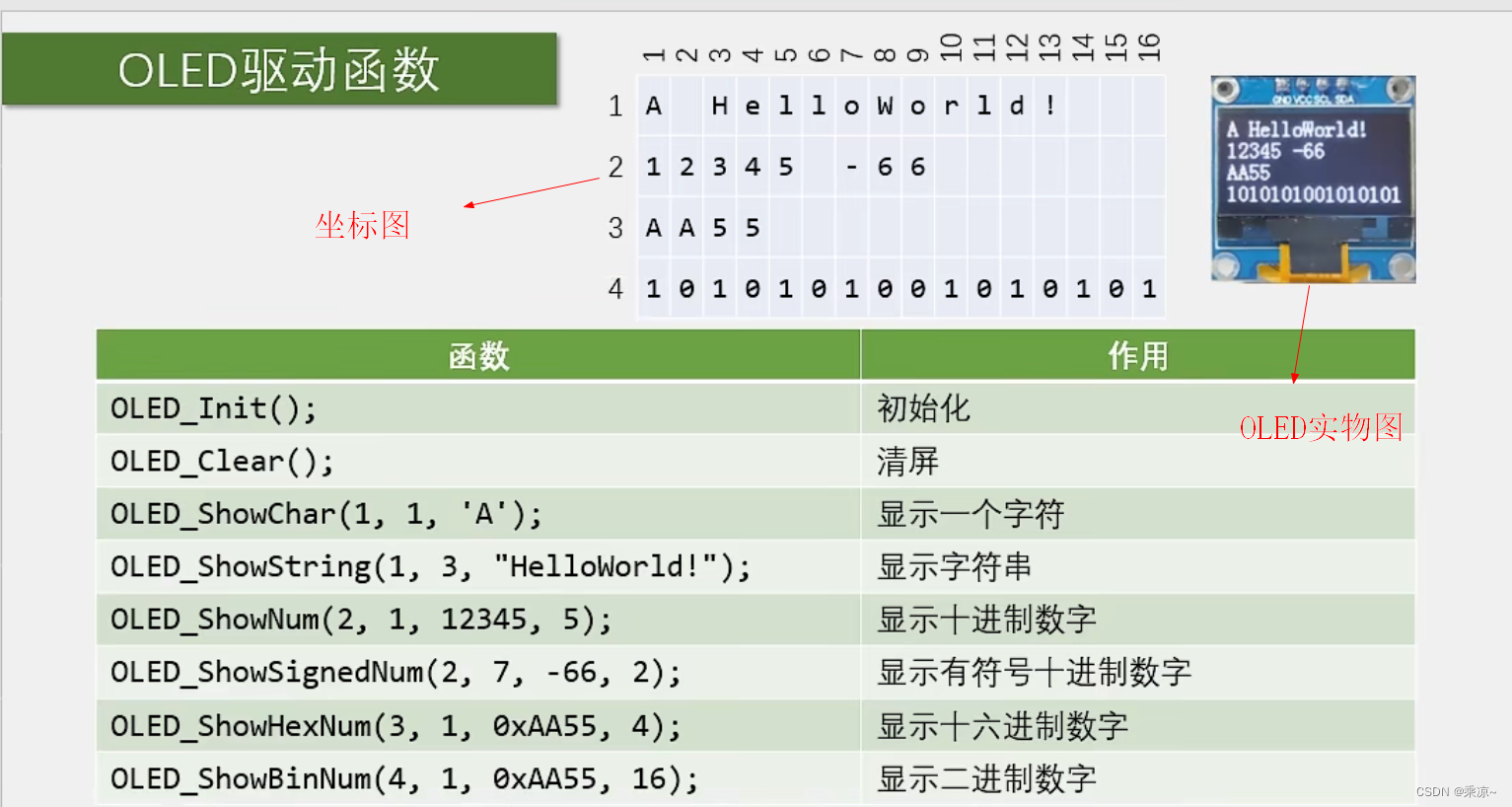
STM32单片机(四)第一节:OLED调试工具
❤️ 专栏简介:本专栏记录了从零学习单片机的过程,其中包括51单片机和STM32单片机两部分;建议先学习51单片机,其是STM32等高级单片机的基础;这样再学习STM32时才能融会贯通。 ☀️ 专栏适用人群 :适用于想要…...

自用的一些网址,码住!
京东羚珑智能抠图网站https://ling.jd.com/live/fm#all:主要用于商品抠图,而且还有多种直播背景设计,非常方便。国外的免费抠图网站https://www.remove.bg/zh/upload:有一个魔法棒的设计,可以自己选择抠图的范围和形状…...

银行vr元宇宙全景虚拟展馆提供更加真实、立体、高效的数字资产交易场景
为了贯彻国家普惠金融政策,使金融如无惠及广大群体,宇宙技术在金融行业中的应用将进一步提升金融消费体验感觉和金融管理水平。打造元宇宙金融服务平台,构建虚实结构的金融服务世界,培育和管理好数字机器人员工队伍,提升金融业务各…...
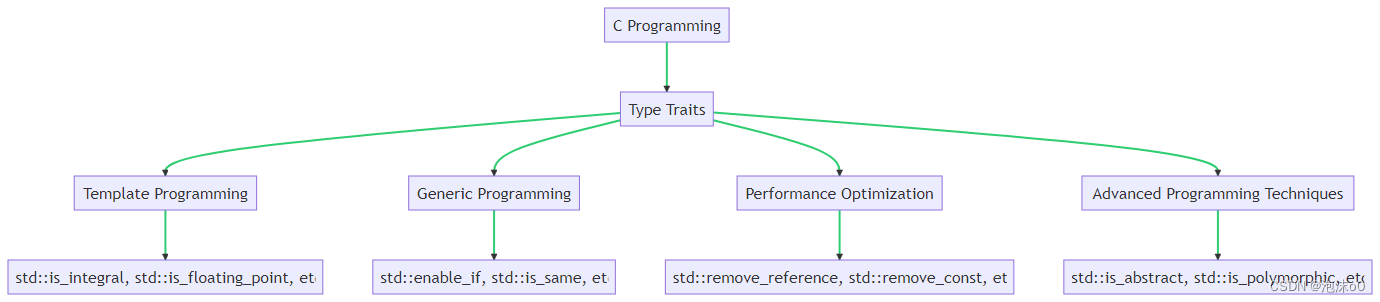
C++ 泛型编程 类型萃取器的运用
C 泛型编程 类型萃取器的运用 一、C类型萃取器的基本概念与应用(Type Traits in C)1.1 类型萃取器的定义与作用(Definition and Role of Type Traits)1.2 类型萃取器的分类与特性(Classification and Characteristics …...
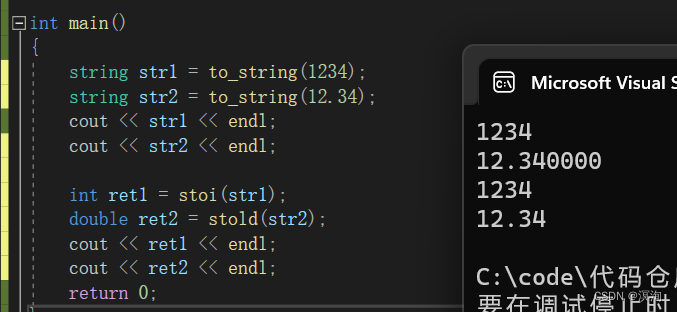
C++ String类(上篇)
绪论 放弃时间的人,时间也会放弃他。——莎士比亚 ; 本篇章是关于string类内一些函数的介绍以及使用方法,都是我们编程必须掌握的基础! 全文共7000字左右. 话不多说安全带系好,发车啦(建议电脑观看&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...
