RL - 强化学习 马尔可夫奖励过程 (MRP) 的状态价值
欢迎关注我的CSDN:https://spike.blog.csdn.net/
本文地址:https://blog.csdn.net/caroline_wendy/article/details/131084795
GitHub 源码: https://github.com/SpikeKing/Reinforcement-Learning-Algorithm
马尔可夫奖励过程 (MRP) 的状态价值是指在某个状态下,从该状态开始,按照某个策略执行动作所能获得的累积奖励的期望值。状态价值反映了状态的优劣,越高的状态价值意味着越好的长期收益。MRP 的状态价值可以通过贝尔曼方程递归地定义和计算。
马尔可夫奖励过程,即MRP,Markov Reward Process;而马尔可夫决策过程,即MDP,Markov Decision Process。
1. 马尔可夫过程 (Markov Process)
随机过程(Stochastic Process)即 P ( S t + 1 ∣ S 1 , . . . , S t ) P(S_{t+1}|S_{1},...,S_{t}) P(St+1∣S1,...,St),马尔可夫过程(Markov Process),即 P ( S t + 1 ∣ S t ) = P ( S t + 1 ∣ S 1 , . . . , S t ) P(S_{t+1}|S_{t}) = P(S_{t+1}|S_{1},...,S_{t}) P(St+1∣St)=P(St+1∣S1,...,St)。
马尔可夫过程: S = s 1 , s 2 , . . s n \mathcal{S}={s_{1},s_{2},..s_{n}} S=s1,s2,..sn 状态集合(State), P \mathcal{P} P 状态转移矩阵(Probability)。给定一个马尔可夫过程,从一个状态出发,可以获得状态序列(episode),即采样(sampling)。
2. 马尔可夫奖励过程 (Markov Reward Process)
马尔可夫奖励过程(Markov Reward Process)由 < S , P , r , γ > <\mathcal{S},\mathcal{P},r,\gamma> <S,P,r,γ> 组成,即增加 r ( s ) r(s) r(s) 表示每个状态的奖励(Return), γ \gamma γ 是折扣因子,随着时间逐渐减弱。
所有奖励的衰减之和,作为 G G G,即 Gain。
G t = R t + γ R t + 1 + γ 2 R t + 2 + . . . = ∑ k = 0 ∞ γ k R t + k G_{t} = R_{t} + \gamma R_{t+1} + \gamma^{2} R_{t+2} + ... = \sum_{k=0}^{\infty}\gamma^{k} R_{t+k} Gt=Rt+γRt+1+γ2Rt+2+...=k=0∑∞γkRt+k
源码:
def compute_return(start_index, chain, gamma, rewards):G = 0for i in reversed(range(start_index, len(chain))):# chain是从1开始,之前奖励G * 折扣因子gamma,再加上当前奖励RG = gamma * G + rewards[chain[i] - 1] return G
3. 贝尔曼方程 (Bellman Equation) 与 状态价值
状态的期望回报,就是这个状态的价值(Value),价值函数:
V ( s ) = E [ G t ∣ S t = s ] V ( s ) = E [ R t + γ V ( S t − 1 ) ∣ S t = s ] V ( s ) = E [ R t ∣ S t = s ] + E [ γ V ( S t − 1 ) ∣ S t = s ] V ( s ) = r ( s ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s ) V ( s ′ ) V(s)=E[G_{t}|S_{t}=s] \\ V(s)=E[R_{t}+\gamma V(S_{t-1})|S_{t}=s] \\ V(s)=E[R_{t}|S_{t}=s]+E[\gamma V(S_{t-1})|S_{t}=s] \\ V(s)=r(s)+\gamma \sum_{s'\in{S}}P(s'|s)V(s') V(s)=E[Gt∣St=s]V(s)=E[Rt+γV(St−1)∣St=s]V(s)=E[Rt∣St=s]+E[γV(St−1)∣St=s]V(s)=r(s)+γs′∈S∑P(s′∣s)V(s′)
即:贝尔曼方程(Bellman Equation)。求解各个状态的价值 V \mathcal{V} V 如下:
V = R + γ P V V = ( I − γ P ) − 1 R \mathcal{V} = \mathcal{R} + \gamma \mathcal{P} \mathcal{V} \\ \mathcal{V} = (\mathcal{I}-\gamma \mathcal{P})^{-1} \mathcal{R} V=R+γPVV=(I−γP)−1R
计算复杂度是 O ( n 3 ) O(n^3) O(n3) ,改进算法包括 动态规划(Dynamic Programming)、蒙特卡洛方法(Monte Carlo Method)、时序差分(Temporal Difference)等。
源码:
def compute(P, rewards, gamma, states_num):"""利用 贝尔曼方程 解析"""rewards = np.array(rewards).reshape((-1, 1)) # 转换成列向量# V = (I - gamma*P)^(-1) * Rvalue = np.dot(np.linalg.inv(np.eye(states_num, states_num) - gamma * P), rewards)return value
相关文章:

RL - 强化学习 马尔可夫奖励过程 (MRP) 的状态价值
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/131084795 GitHub 源码: https://github.com/SpikeKing/Reinforcement-Learning-Algorithm 马尔可夫奖励过程 (MRP) 的状态价值是指在某…...

Mybatis之批处理流式查询
文章目录 1 批处理查询1.1 引言1.2 流式查询1.2.1 定义1.2.2 流式查询接口1.2.3 使用流式查询关闭问题1.2.3.1 SqlSessionFactory1.2.3.2 TransactionTemplate1.2.3.3 Transactional 注解 1.2.4 完整示例1.2.4.1 mapper接口和SQL1.2.4.2 Service操作 1.3 游标查询1.3.1 定义1.3…...
Spring架构篇--2.7.3 远程通信基础--Netty原理--bind实现端口的绑定
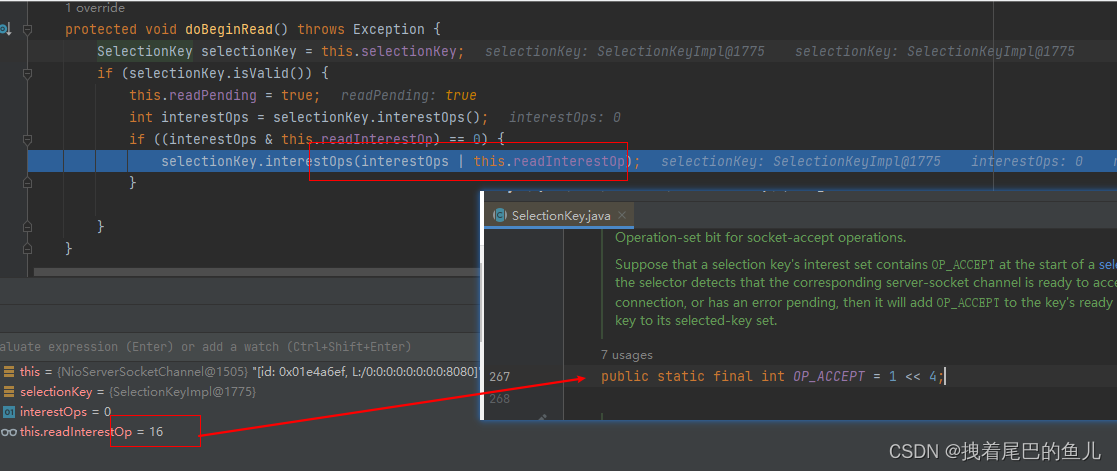
前言:在对ServerBootstrap 进行属性赋值之后,通过bind 方法完成端口的绑定,并开始在NioEventLoop中进行轮询进行事件的处理;本文主要探究ServersocketChannel 在netty 中是如何完成注册,以及端口的绑定 1 Nio selecto…...

【改进的多同步挤压变换】基于改进多同步挤压的高分辨率时频分析工具,用于分析非平稳信号(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

有关 python 切片的趣事
哈喽大家好,我是咸鱼 今天来讲一个我在实现 python 列表切片时遇到的趣事 在正式开始之前,我们先来了解一下切片(slice) 切片操作是访问序列(列表、字符串…)中元素的另一种方法,它可以访问一…...

ChatGPT 会带来失业潮吗?
(永久免费,扫码加入) 最近在翻知乎上的一些文章,很多都是跟ChatGPT有关的。因为本身是搞Python编程的,知乎推荐系统给我推荐了一篇廖雪峰老师的文章,觉得很有意思。 一共1119个赞,还是很厉害的&…...

如何对待工作中的失误
在日复一日的工作中,我们免不了会产生一些失误,会因此感到沮丧和失望。但如何正确地对待和处理这些失误才是最重要的,它直接影响到我们的工作表现和个人成长。一起来谈谈作为职场人的你时如何处理工作中的失误的吧! 一、在面对失…...

微信小程序快速入门【一】
微信小程序快速入门【一】 文章目录 微信小程序快速入门【一】👨🏫内容1:背景👨⚖️内容2:准备工作👨💻内容3:新建一个小程序🍉文末推荐 👨…...
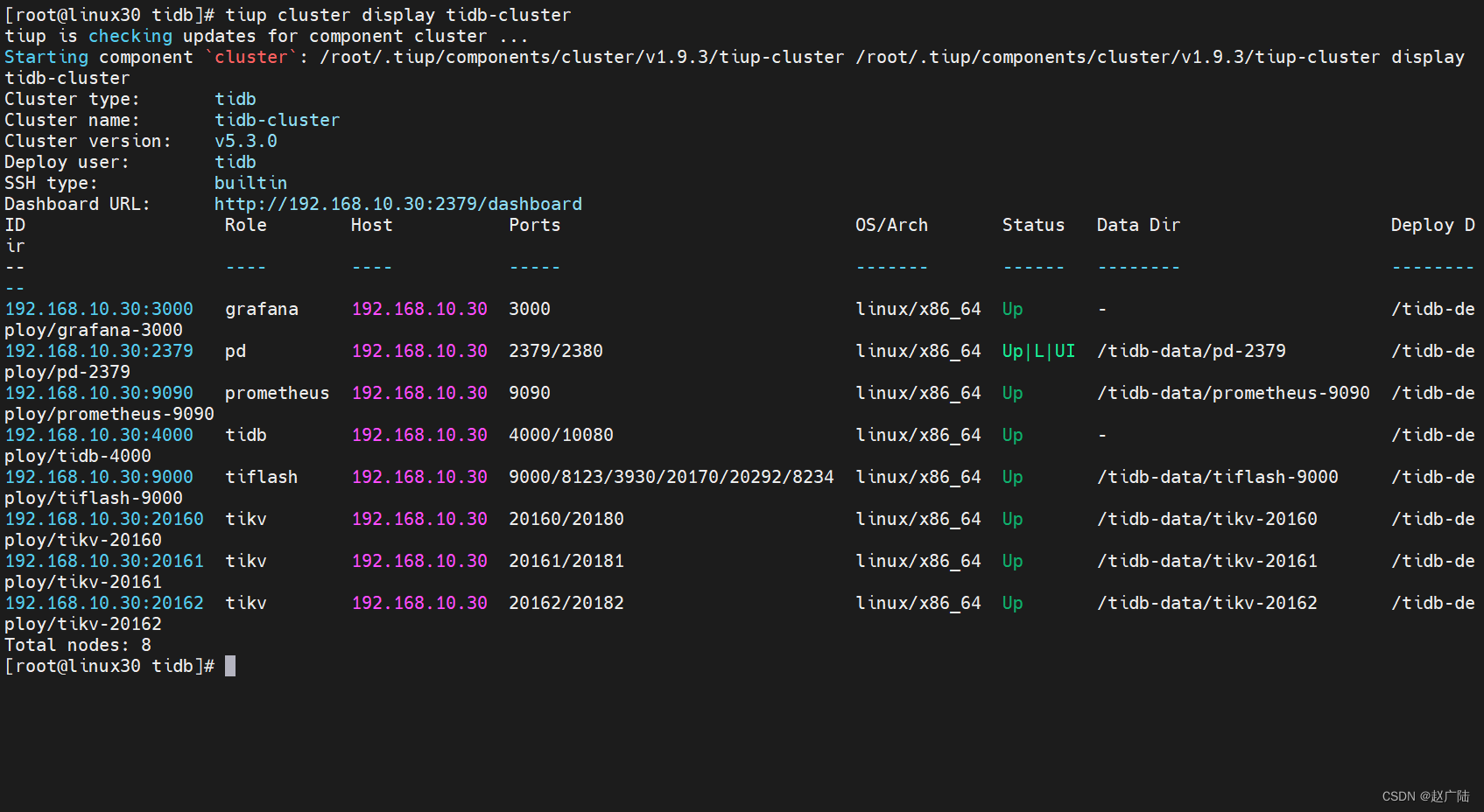
TiDB亿级数据亚秒响应查询集群部署
目录 1 集群部署1.1 环境要求1.1.1 操作系统建议配置1.1.2 服务器建议配置 1.2 环境准备1.3 安装TiUP1.3.1 什么是TiUP1.3.2 安装TiUP组件1.3.3 配置TiUP环境1.3.4 检查TiUP 工具是否安装1.3.5 安装 cluster 组件1.3.6 升级cluster组件 1.4 编辑部署文件1.4.1 常见的部署场景1.…...

并发——同步访问共享的可变数据
关键字 synchronized 可以保证在同一时刻,只有一个线程可以执行某一个方法,或者某一段代码块。许多程序员把同步的概念仅仅理解为一种互斥的方式。即,当一个对象被一个线程修改的时候,可以阻止另一个线程观察到内部不一致的状态。…...
禁用容器网络)
Docker网络模型(九)禁用容器网络
禁用容器网络 如果你想完全禁用容器上的协议栈,你可以在启动容器时使用 --network none 标志。在容器内,只有回环设备被创建。下面的例子说明了这一点。 创建容器 $ docker run --rm -dit \--network none \--name no-net-alpine \alpine:latest \ash通…...

JavaScript 教程---互联网文档计划
学习目标: 每天记录一章笔记 学习内容: JavaScript 教程---互联网文档计划 笔记时间: 2023-6-5 --- 2023-6-11 学习产出: 1.入门篇 1、JavaScript 的核心语法包含部分 基本语法标准库宿主API 基本语法:比如操作符…...

做好功能测试需要的8项基本技能【点工进来】
功能测试是测试工程师的基础功,很多人功能测试还做不好,就想去做性能测试、自动化测试。很多人对功能测试的理解就是点点点,如何自己不用心去悟,去研究,那么你的职业生涯也就停留在点点点上了。在这里,我把…...
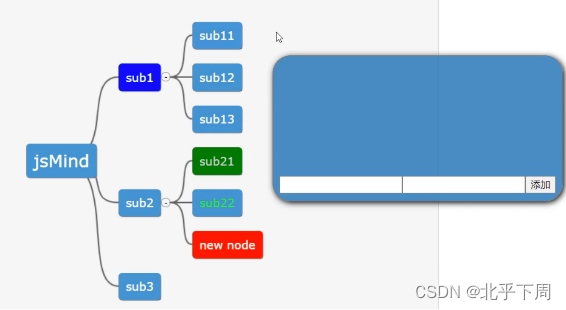
在弹出框内三个元素做水平显示
最终效果图要求是这样: js代码: // 显示弹出窗口 function showPopup(node) {var popup document.createElement(div);popup.className popup;var inputContainer1 document.createElement(div);/* inputContainer1.className input-container1; */…...

纠删码技术在vivo存储系统的演进【上篇】
作者:vivo 互联网服务器团队- Gong Bing 本文将学术界和工业界的纠删码技术的核心研究成果进行了相应的梳理,然后针对公司线上存储系统的纠删码进行分析,结合互联网企业通用的IDC资源、服务器资源、网络资源、业务特性进行分析对原有纠删码技…...
如何实现APP自动化测试?
APP测试,尤其是APP的自动化测试,在软件测试工程师的面试中越来越会被问到了。为了更好的回答这个问题,我今天就给大家分享一下,如何进行APP的自动化测试。 一、为了实现JavaAppiumJunit技术用于APP自动化测试,所以需要…...

INNODB和MyISAM区别
1 存储引擎是MyISAM 如下: CREATE table test_myisam (cli int ) ENGINEMyISAM 存储目录里会有三个文件 test_myisam.frm为“表定义”,是描述数据表结构的文件 test_myisam.MYI文件是表的索引 test_myisam.MYD文件是表的数据 2 存储引擎是INNODB…...
普中自动下载软件1.86下载程序失败案例
今天在用开发板做一个功能,下载的时候报错了,说芯片超时 确定驱动安装好了的 波特率也试了一圈 线也换过了 最后发现是芯片类型选错了,这个开发板是用的stc89c52,所以我选了图里这个,但是翻了开发板配套的资料,发现…...

JavaScript HTML DOM
JavaScript HTML DOM(文档对象模型)是一种用于访问和操作HTML文档元素的编程接口。它将HTML文档表示为一个树形结构,使开发人员可以使用JavaScript来操作和修改HTML元素、属性、样式和事件。 通过使用HTML DOM,你可以使用JavaScr…...
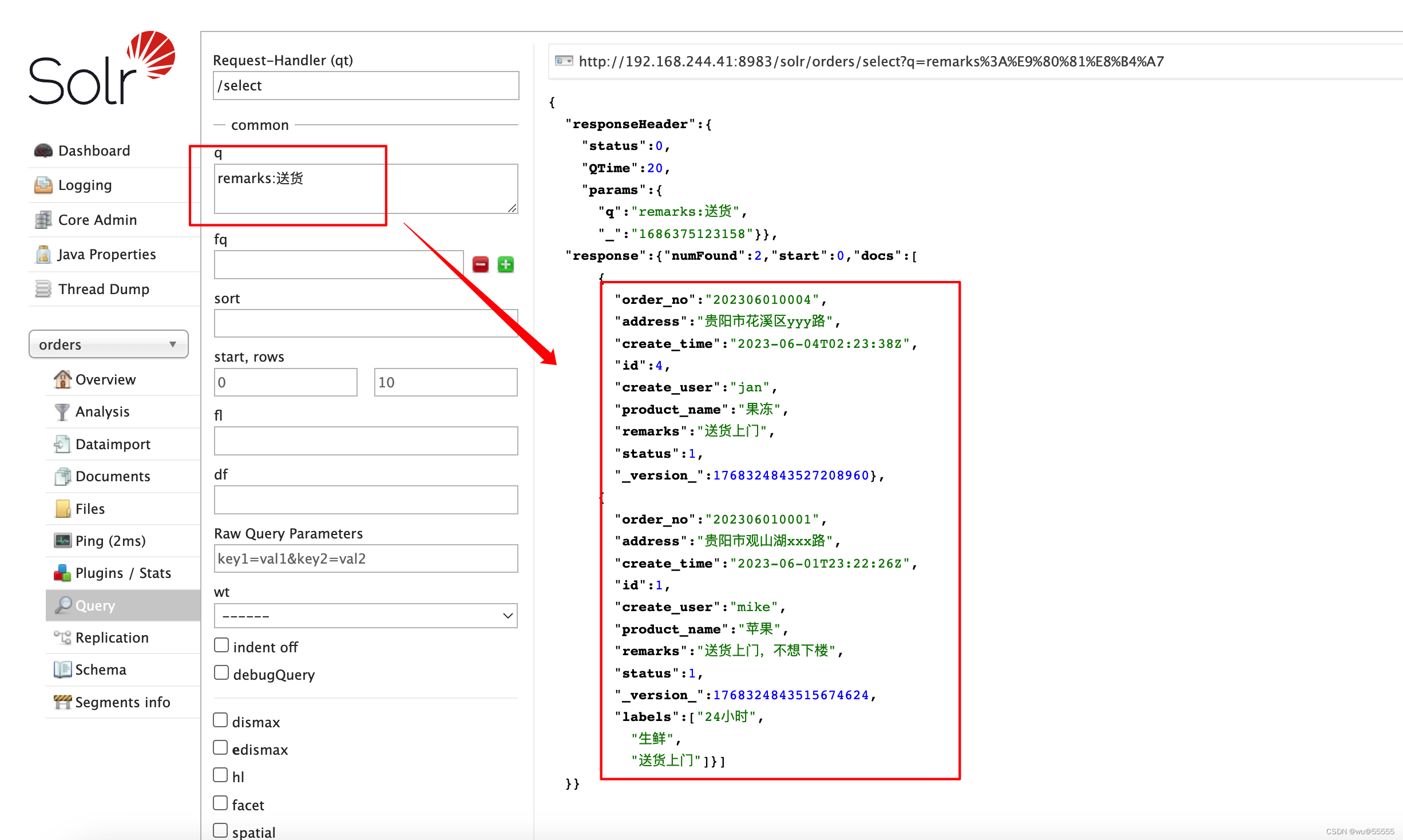
solr快速上手:配置IK中文分词器(七)
0. 引言 solr作为搜索引擎,常用在我们对于搜索速度有较高要求且大数据量的业务场景,我们之前已经配置过英文分词器,但是针对中文分词不够灵活和实用,要实现真正意义上的中文分词,还需要单独安装中文分词器 solr快速上…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
