第六十八天学习记录:高等数学:导数(宋浩板书)
导数是微积分中的一个概念,描述了函数在某一个点上的变化率。具体地说,函数 f ( x ) f(x) f(x)在 x = a x=a x=a处的导数为 f ′ ( a ) f'(a) f′(a),表示当 x x x在 a a a处发生微小的变化 Δ x \Delta x Δx时, f ( x ) f(x) f(x)对应的值 f ( a ) f(a) f(a)相应地发生的变化 Δ f \Delta f Δf与 Δ x \Delta x Δx的比值,即:
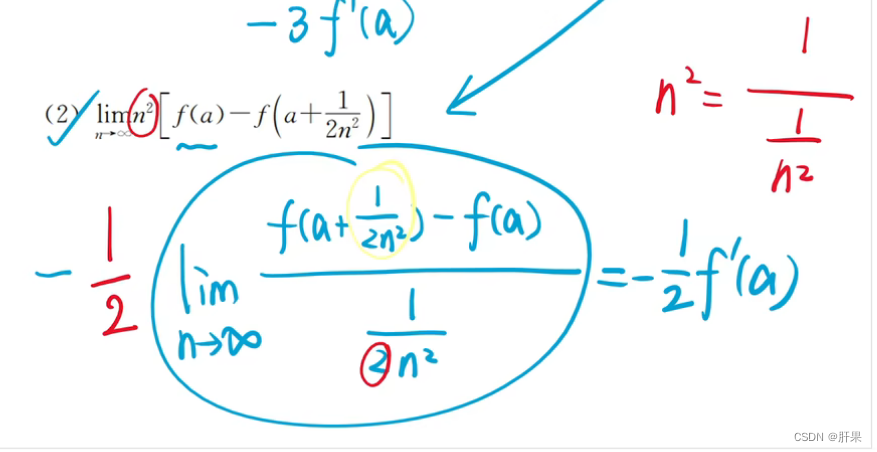
f ′ ( a ) = lim Δ x → 0 Δ f Δ x = lim Δ x → 0 f ( a + Δ x ) − f ( a ) Δ x f'(a) = \lim_{\Delta x\to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x\to 0} \frac{f(a+\Delta x) - f(a)}{\Delta x} f′(a)=Δx→0limΔxΔf=Δx→0limΔxf(a+Δx)−f(a)
导数可以帮助我们判断函数在某一个点上是递增还是递减,并且可以用来求极值和确定函数的曲线形状等。具体地说,如果导数 f ′ ( x ) f'(x) f′(x)在 x = a x=a x=a处为正,则说明函数在该点附近是递增的;如果导数 f ′ ( x ) f'(x) f′(x)在 x = a x=a x=a处为负,则说明函数在该点附近是递减的;如果导数 f ′ ( x ) f'(x) f′(x)在 x = a x=a x=a处为零,可能是函数的局部极值点或拐点。

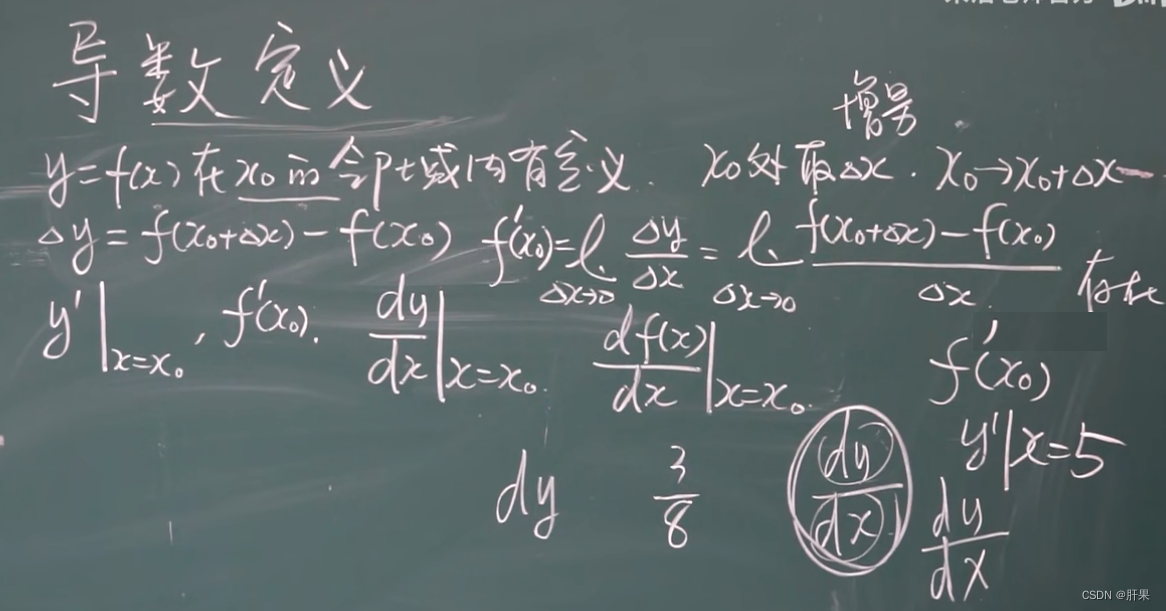
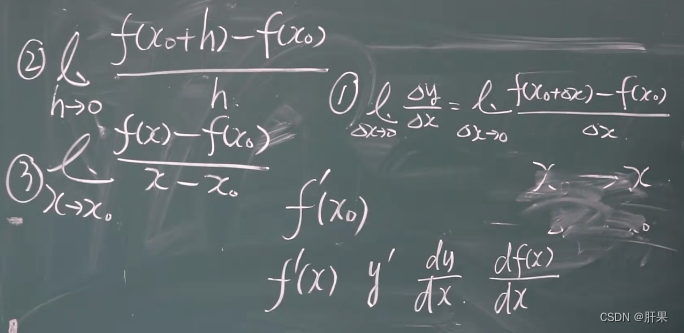
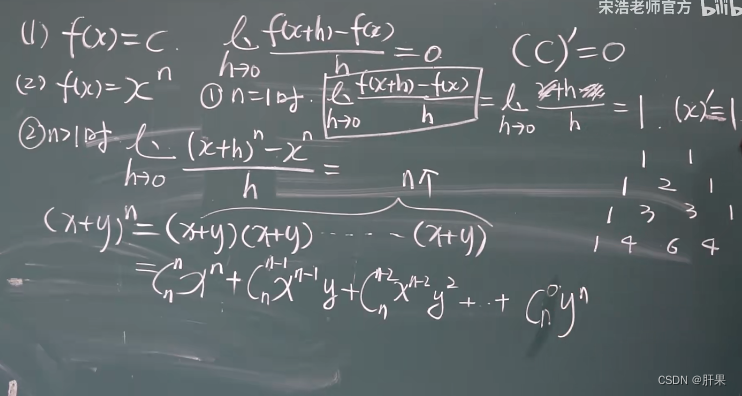
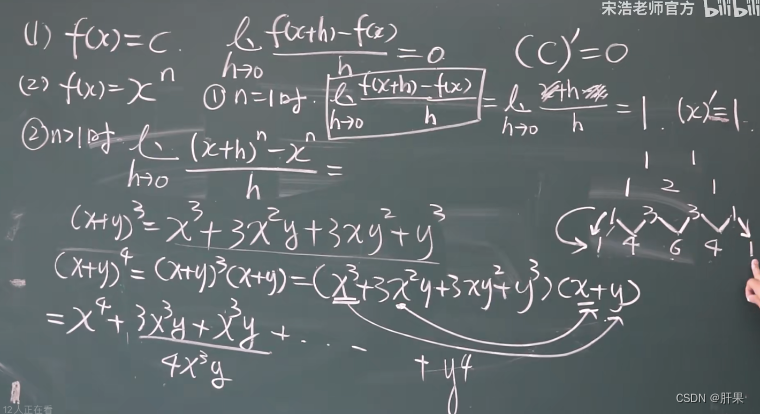
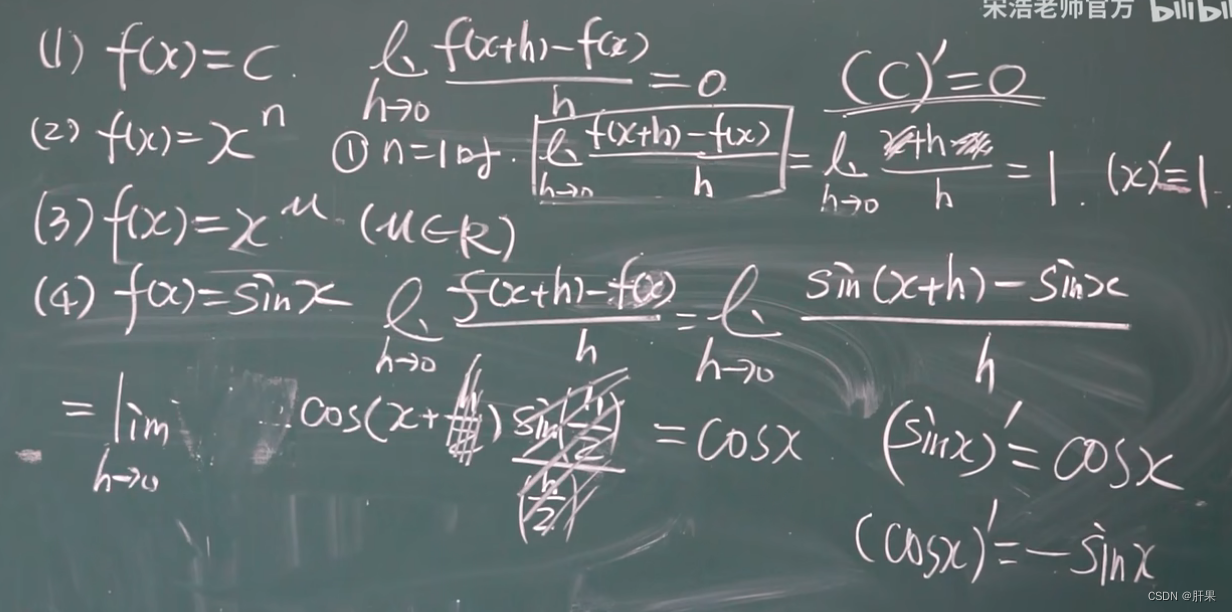
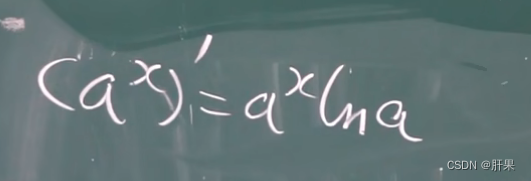
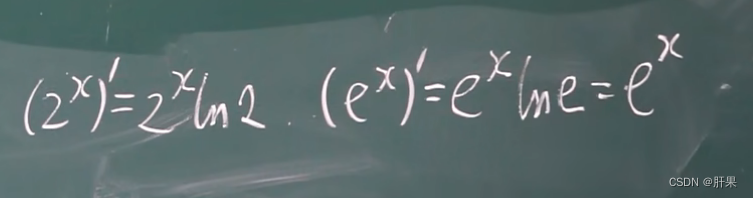
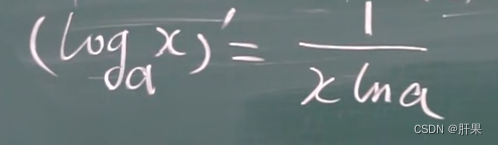
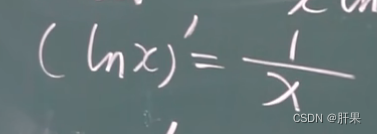
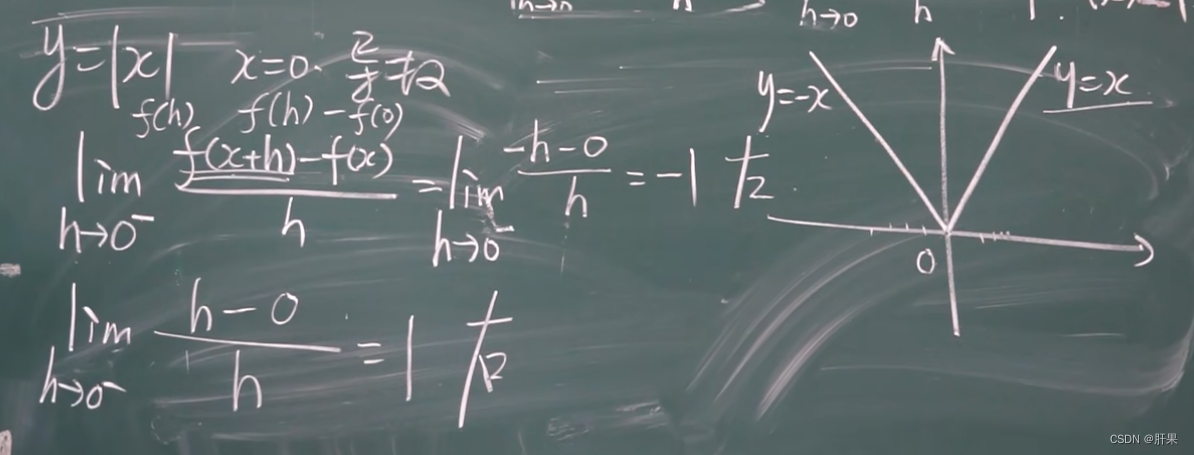
单侧导数
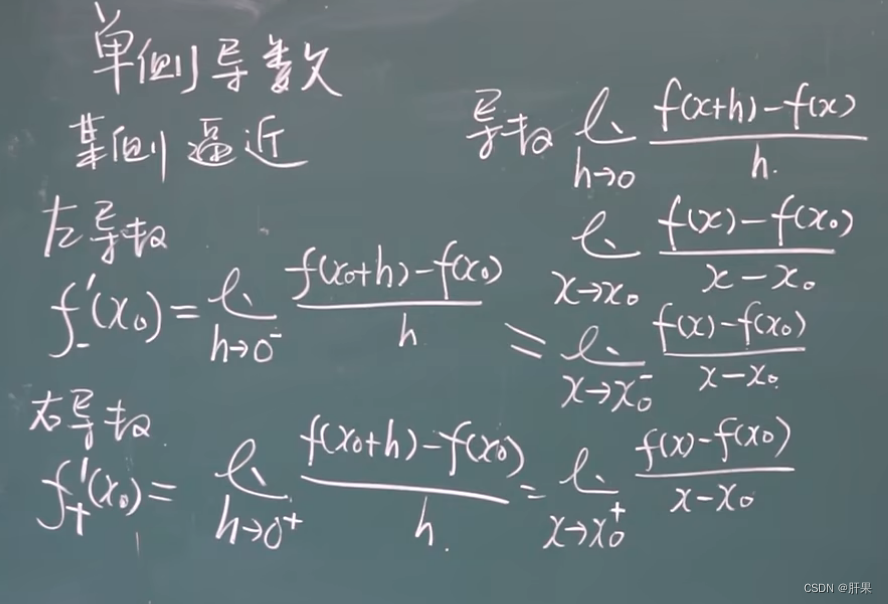

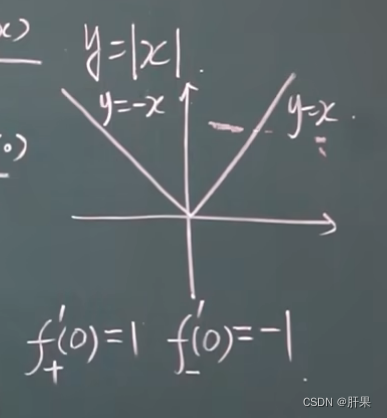

导数的几何含义
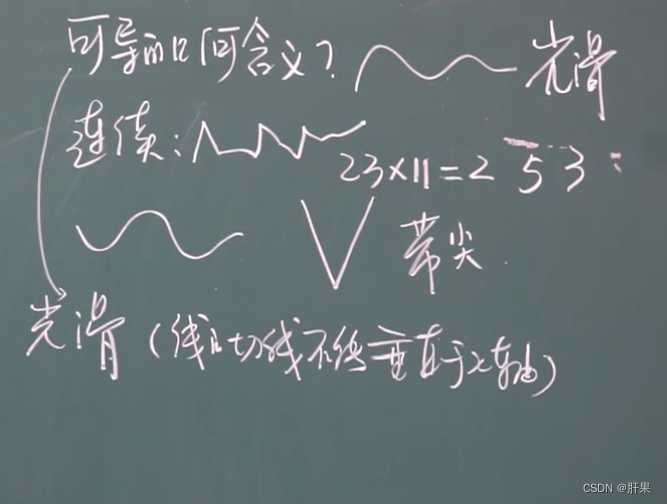
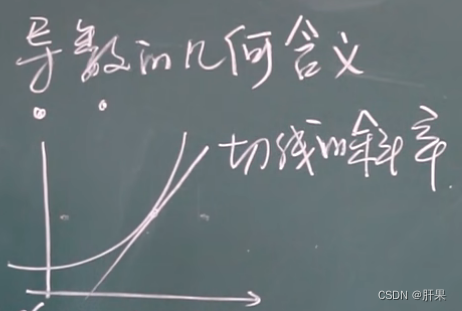
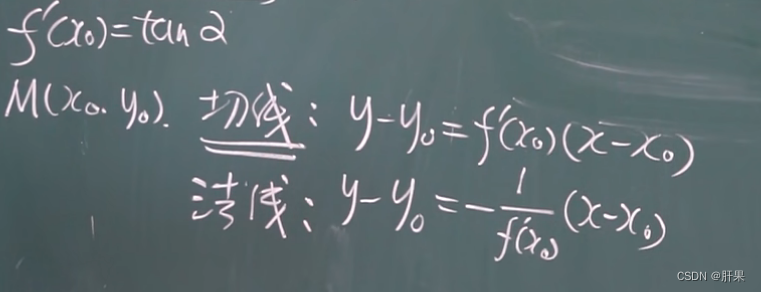
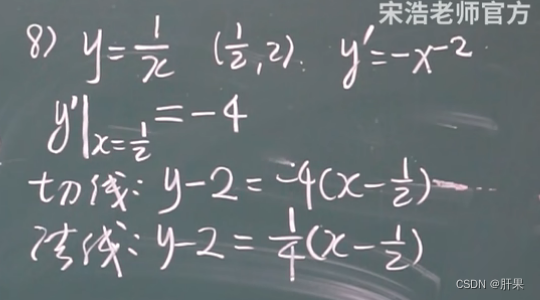
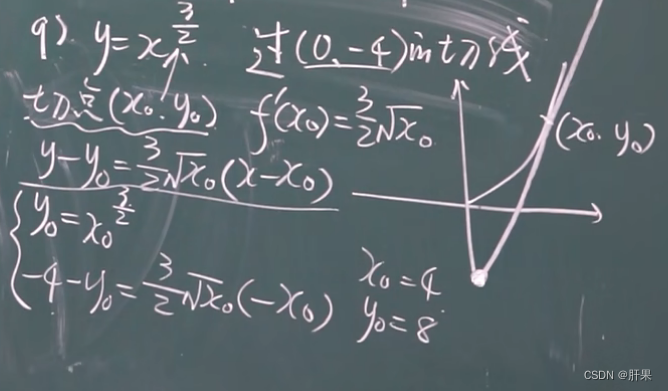

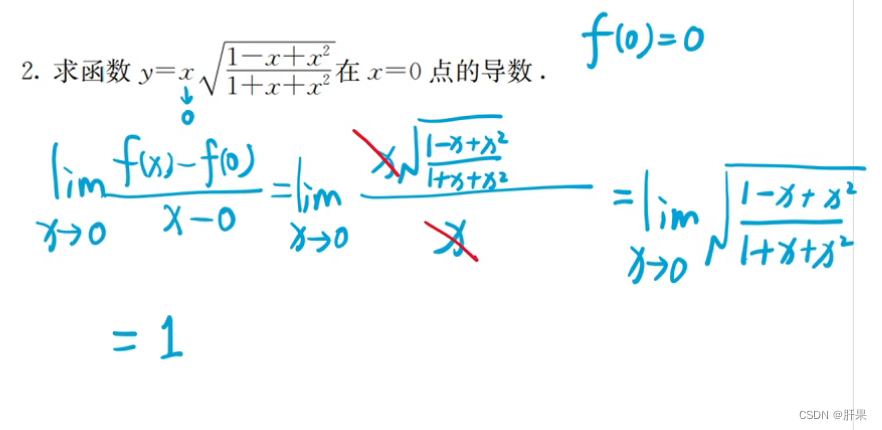
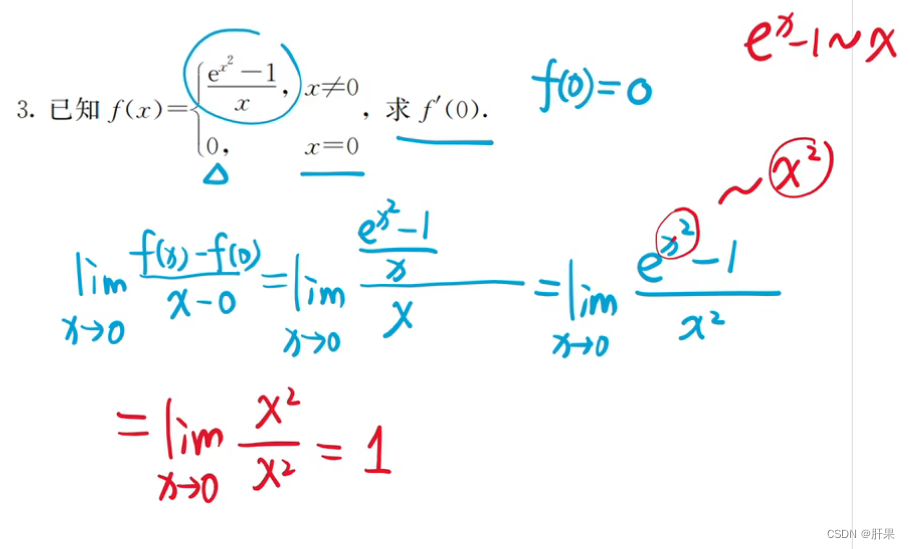

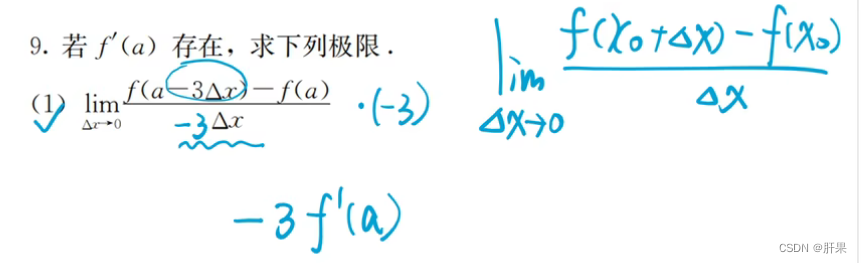



可导与连续的关系

求导法则 和差积商(本章最重要)
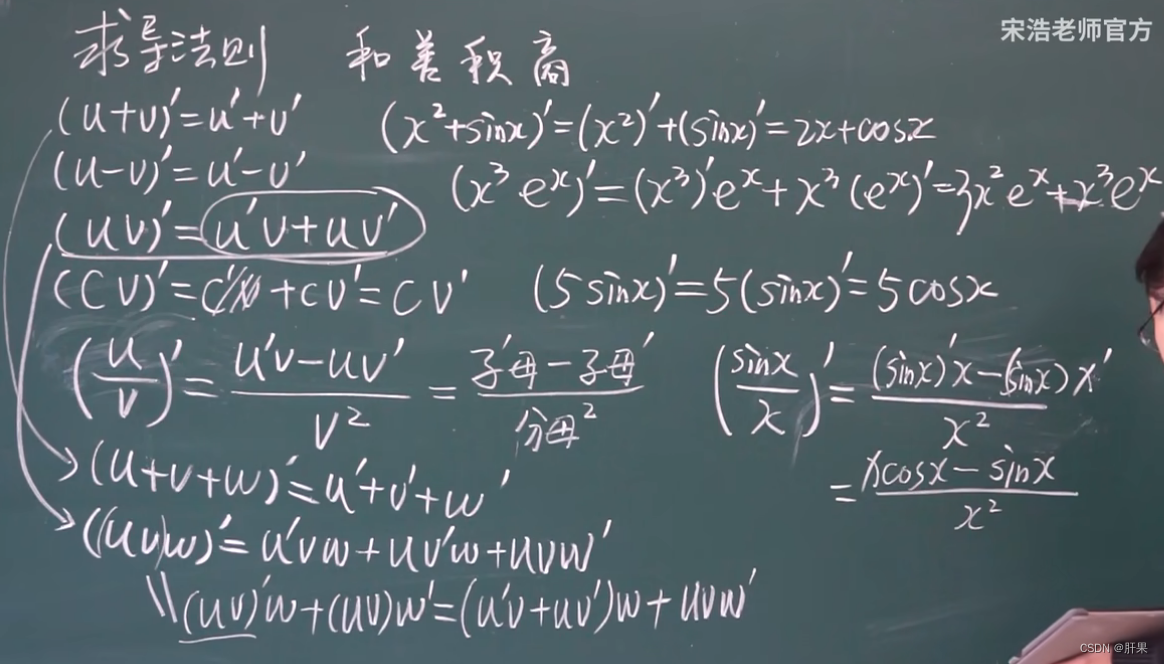

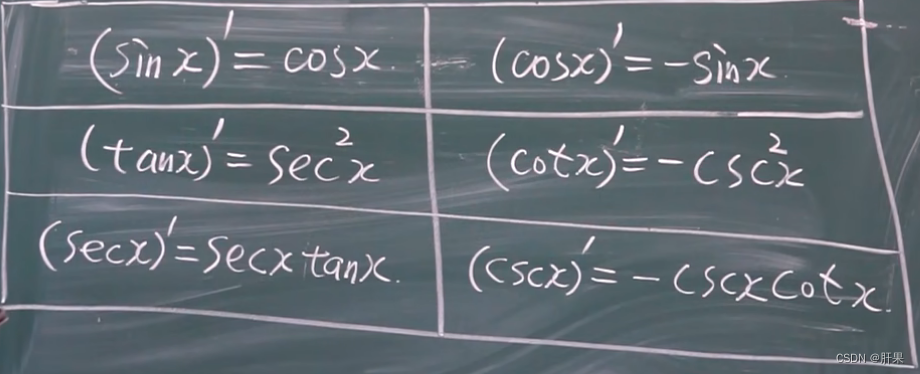

反函数的求导法则
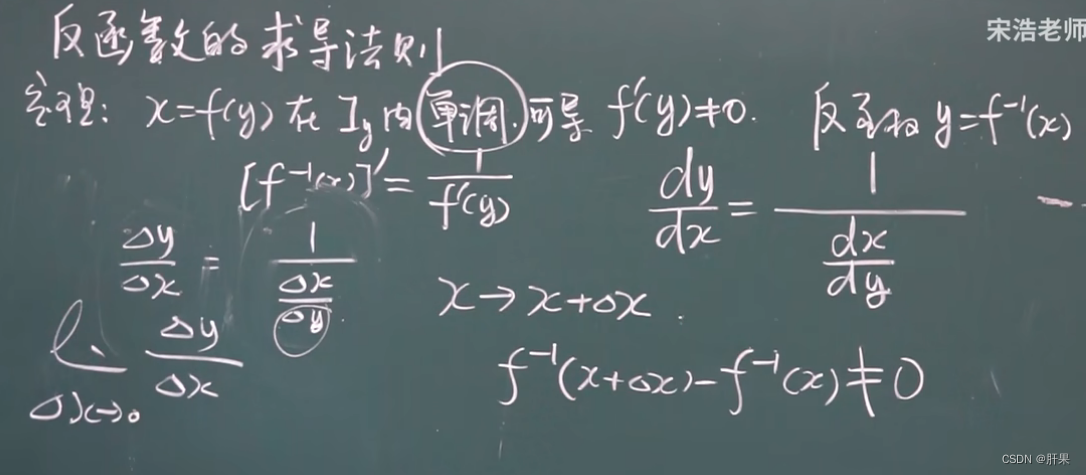
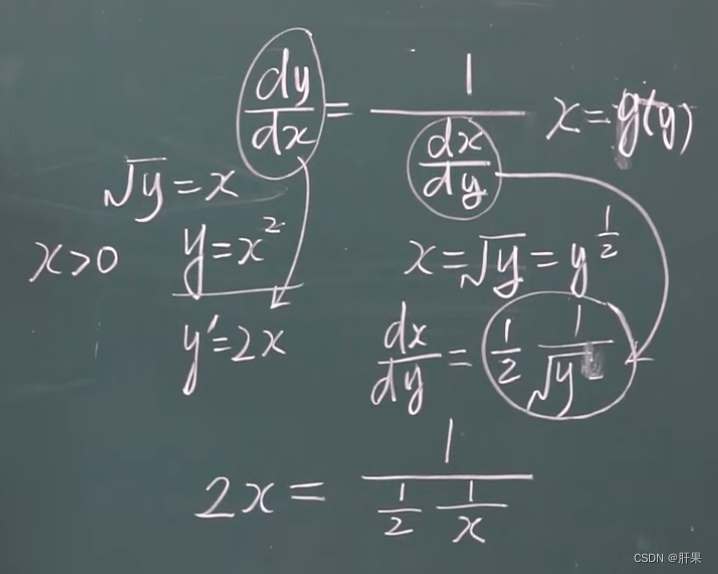

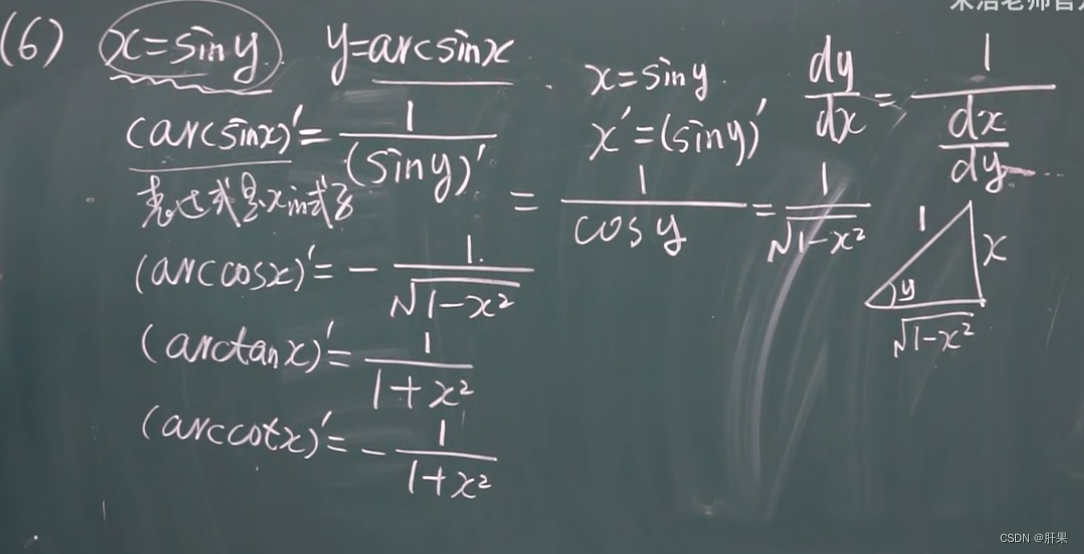
复合函数的求导(链式法则)


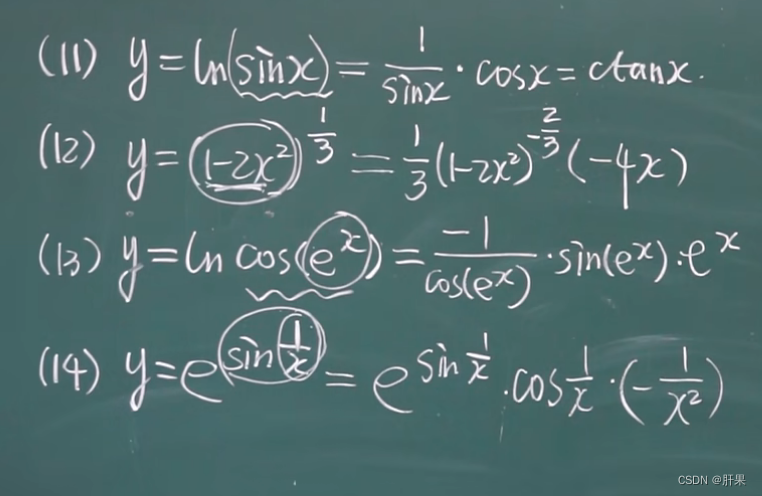
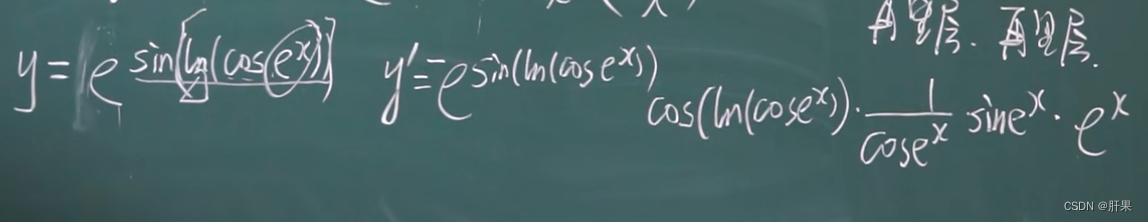
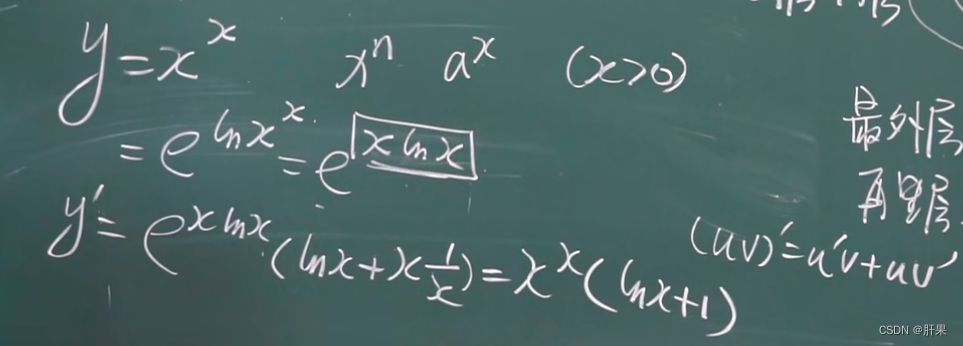
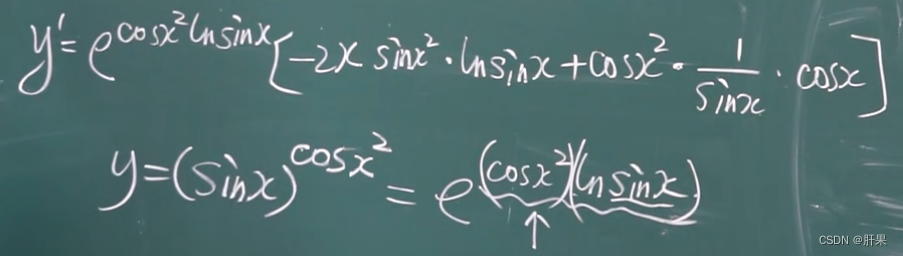
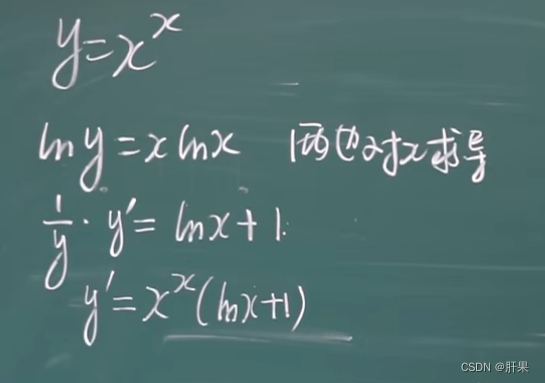
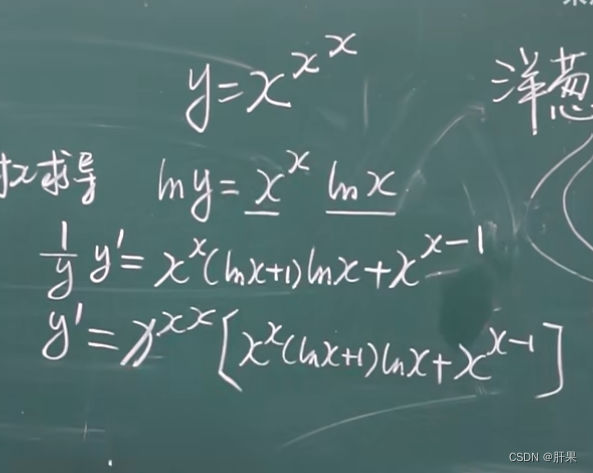
导数公式(重点)
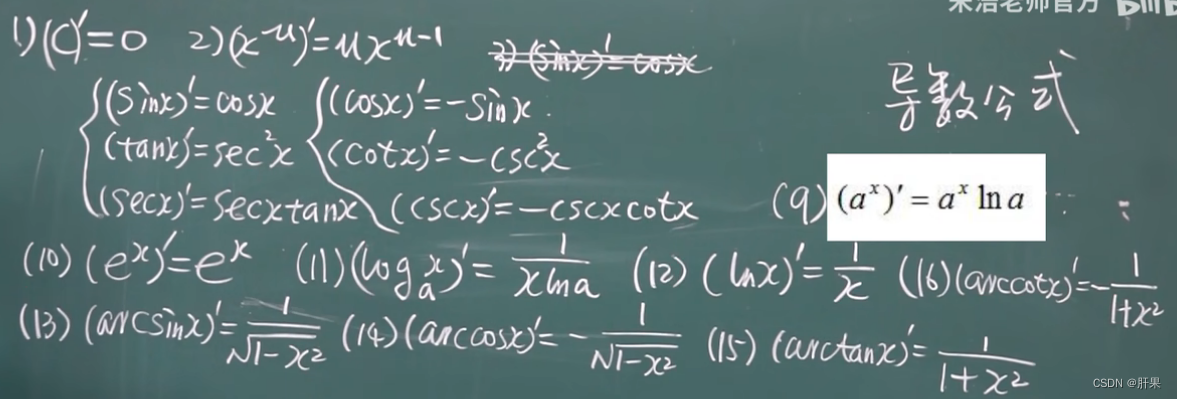
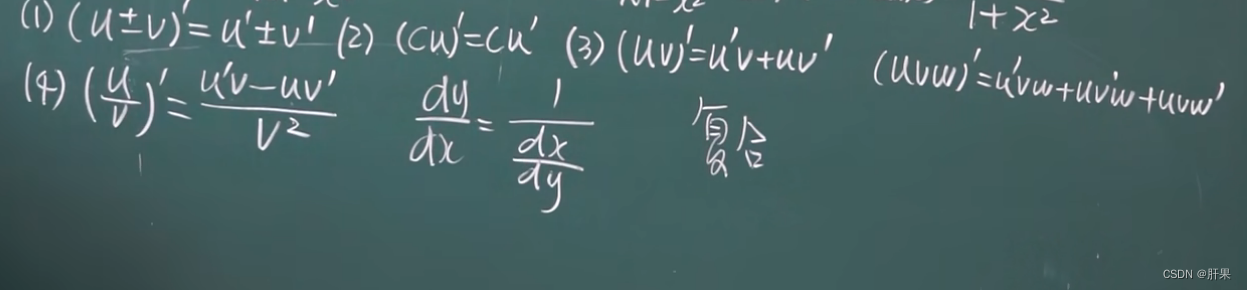
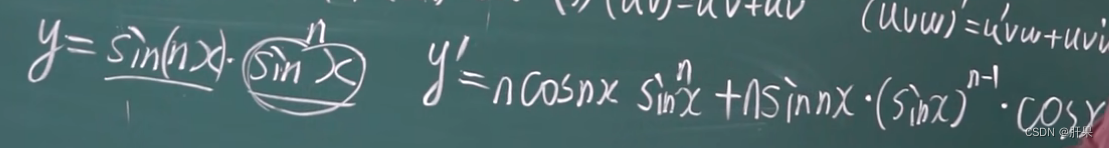
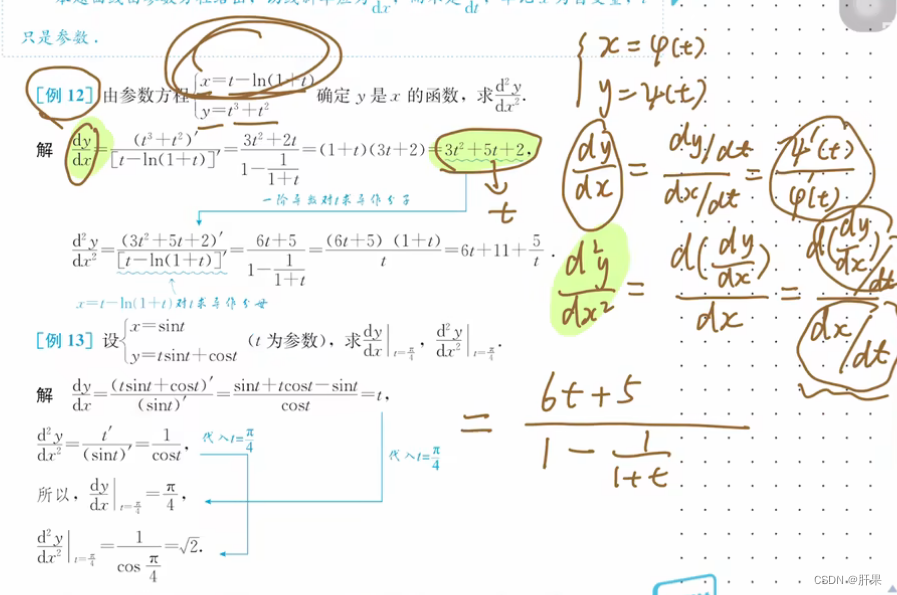
高阶导数
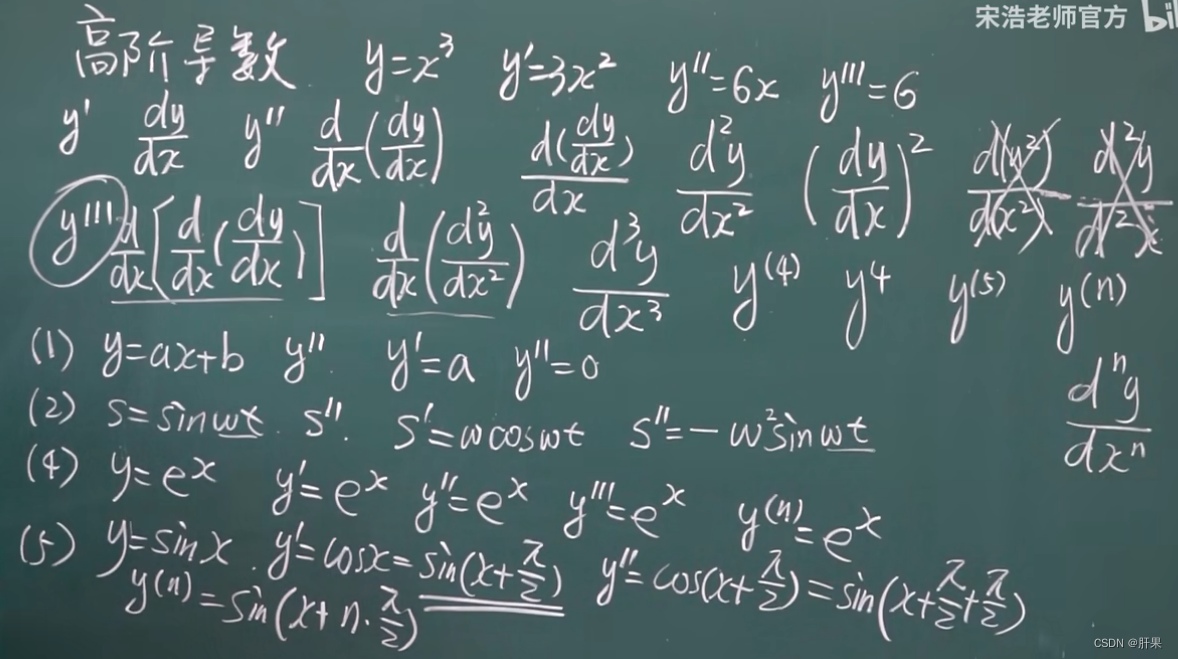
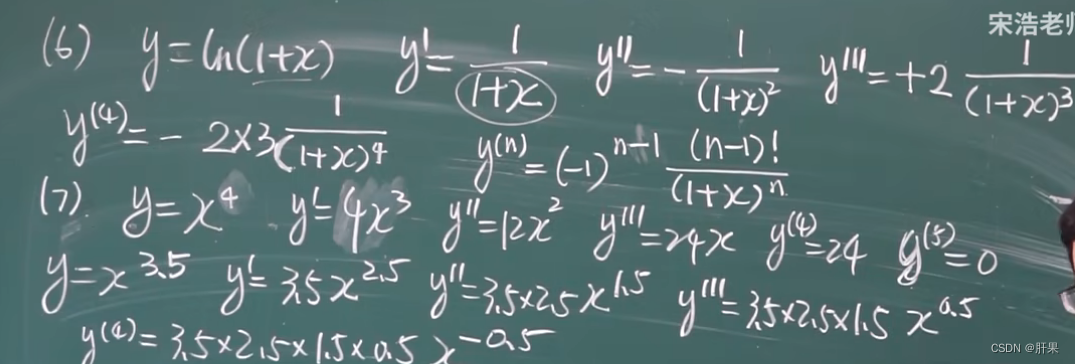
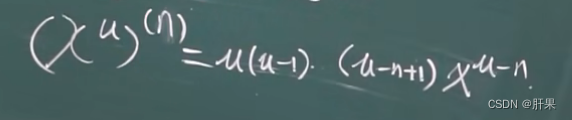
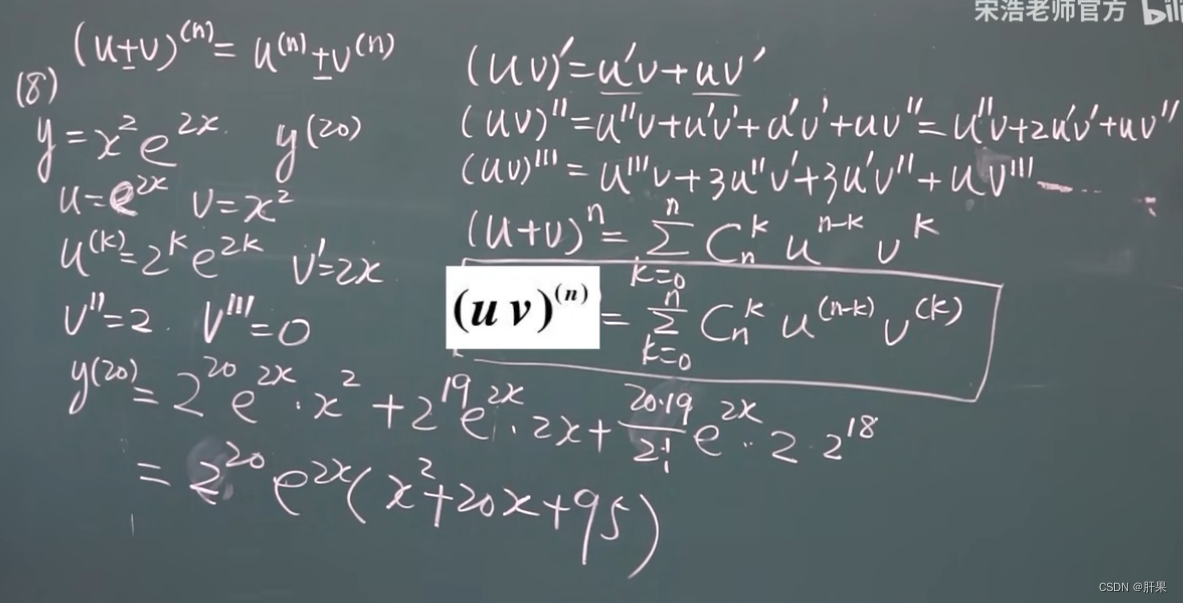
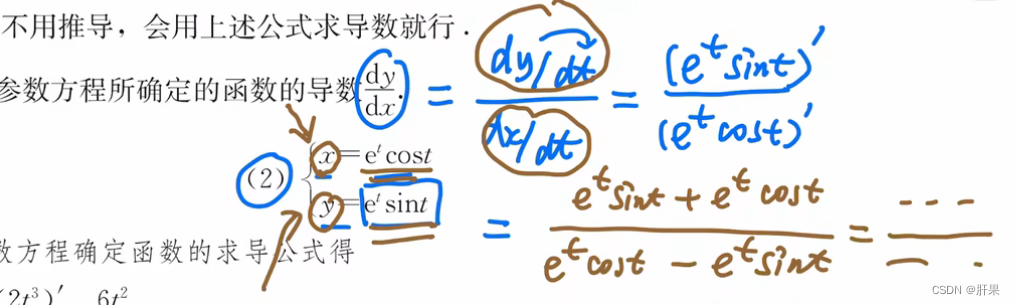
隐函数求导
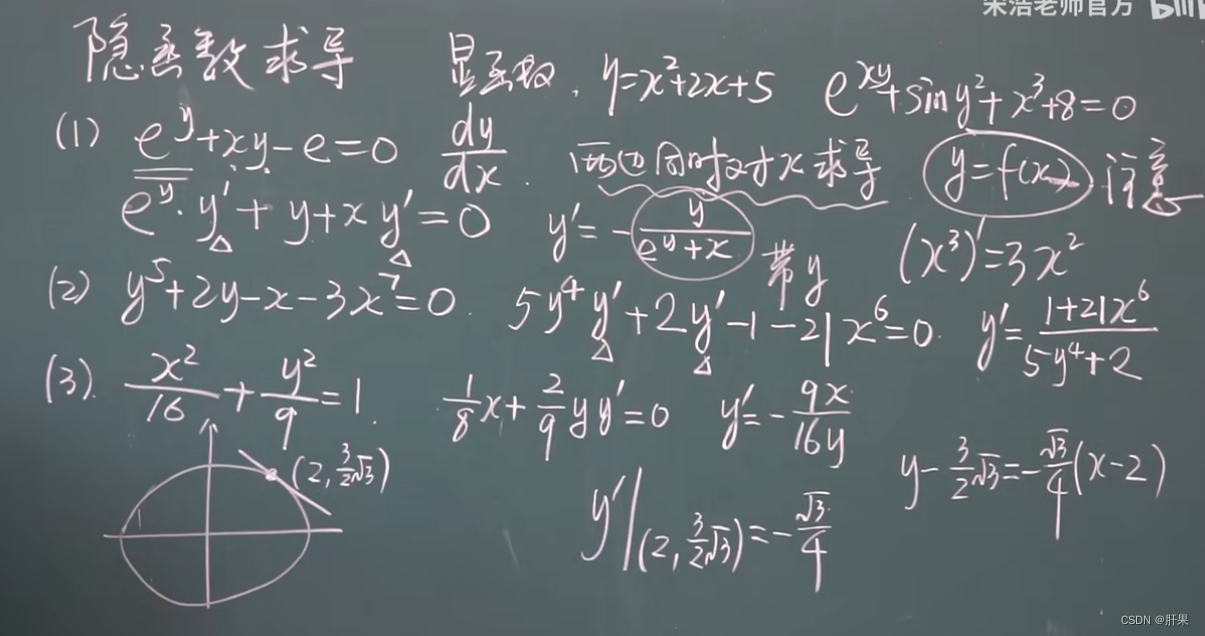
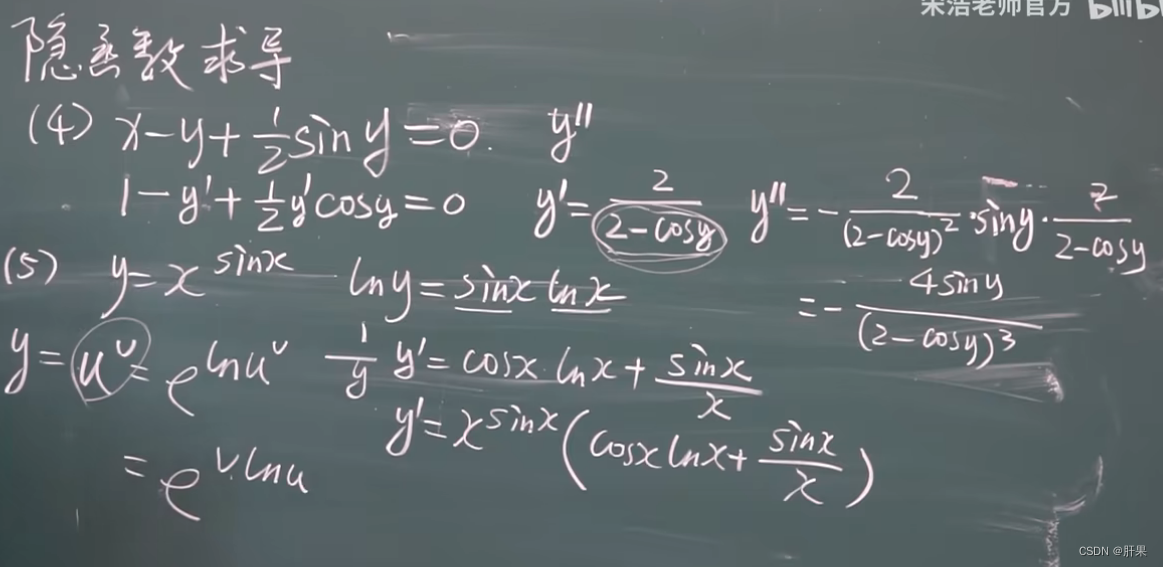
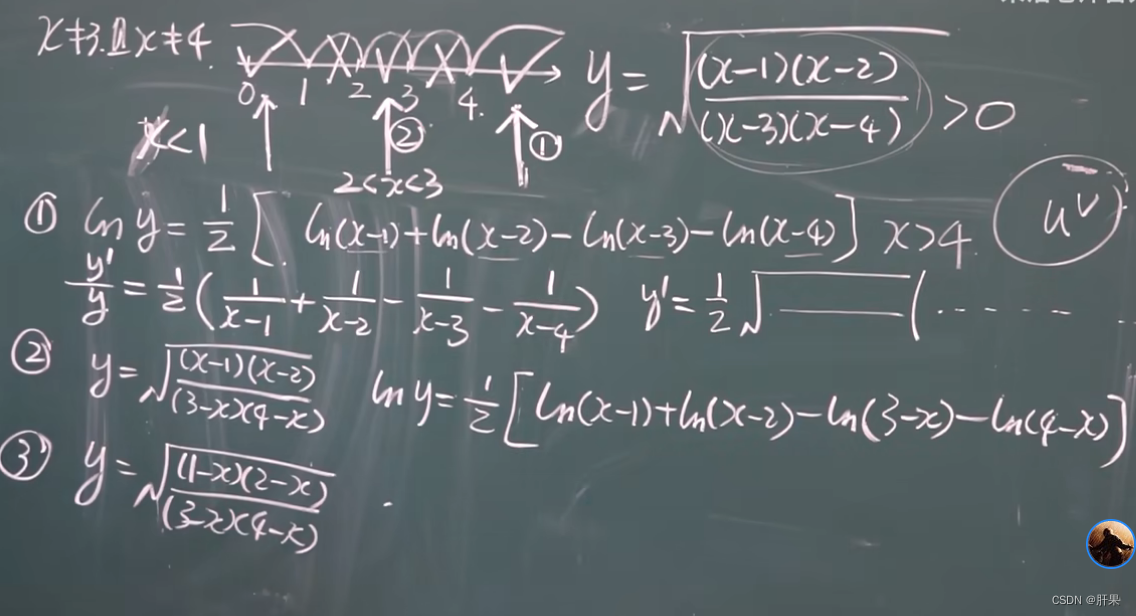
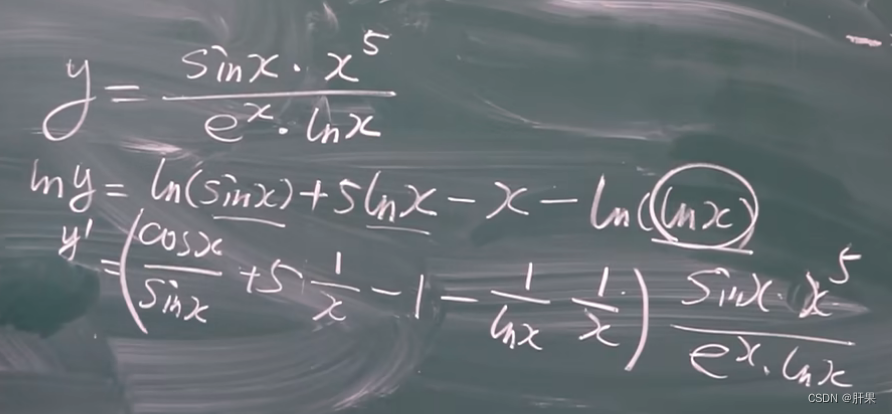


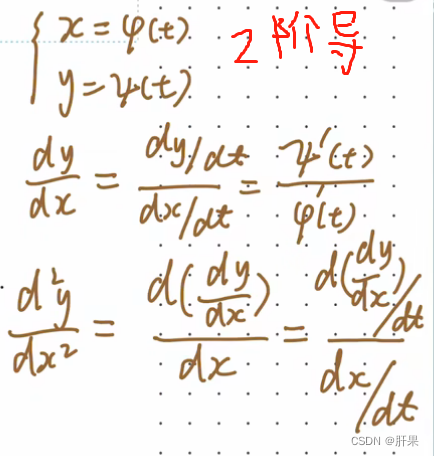

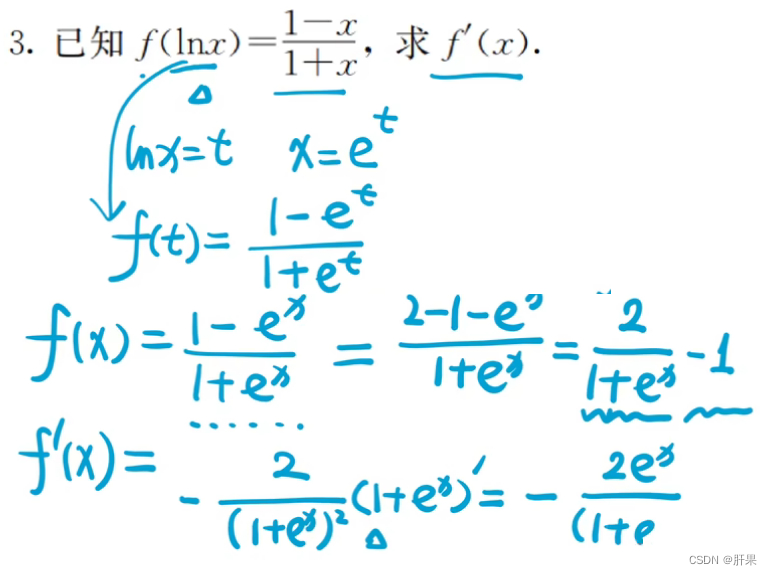

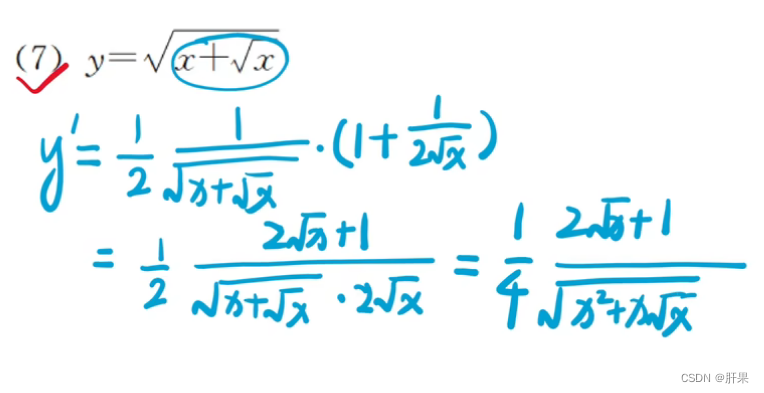

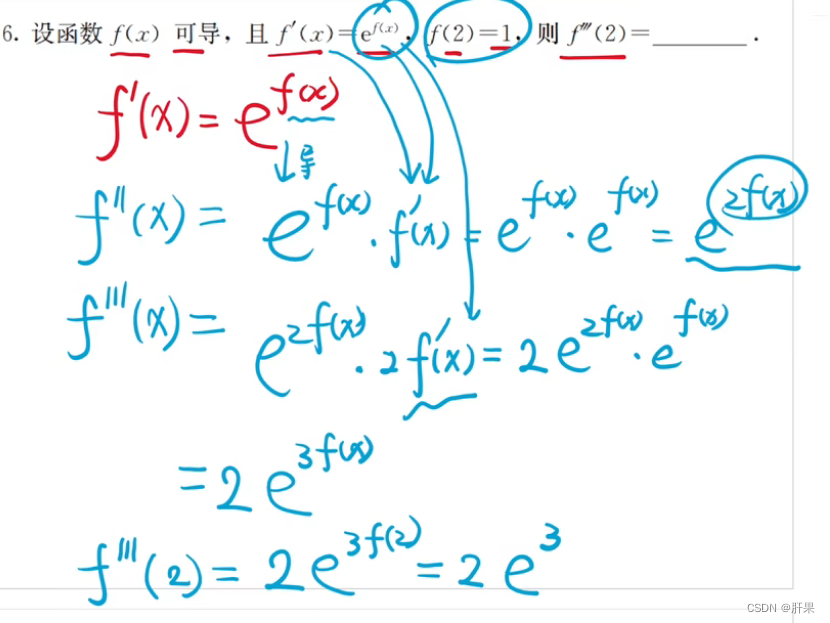

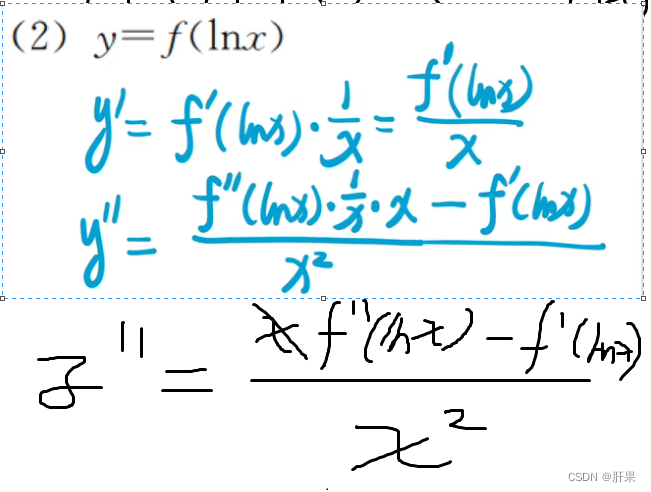
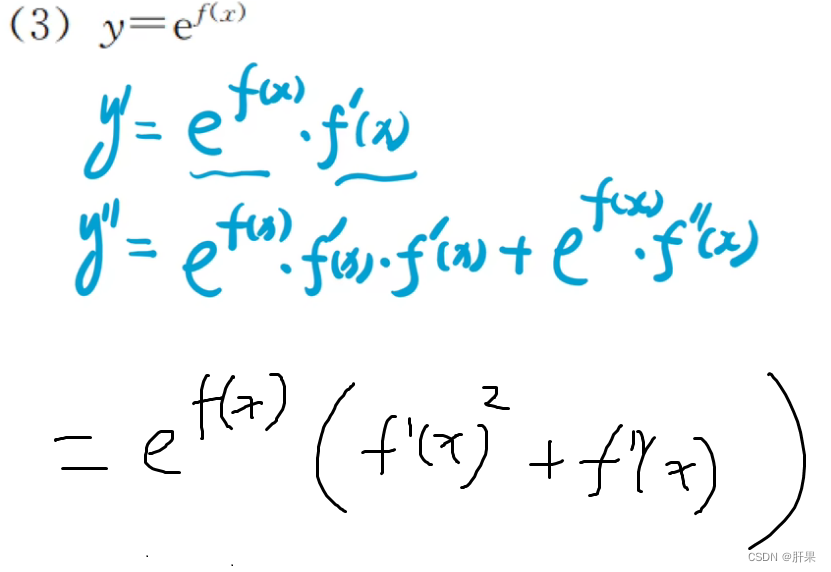
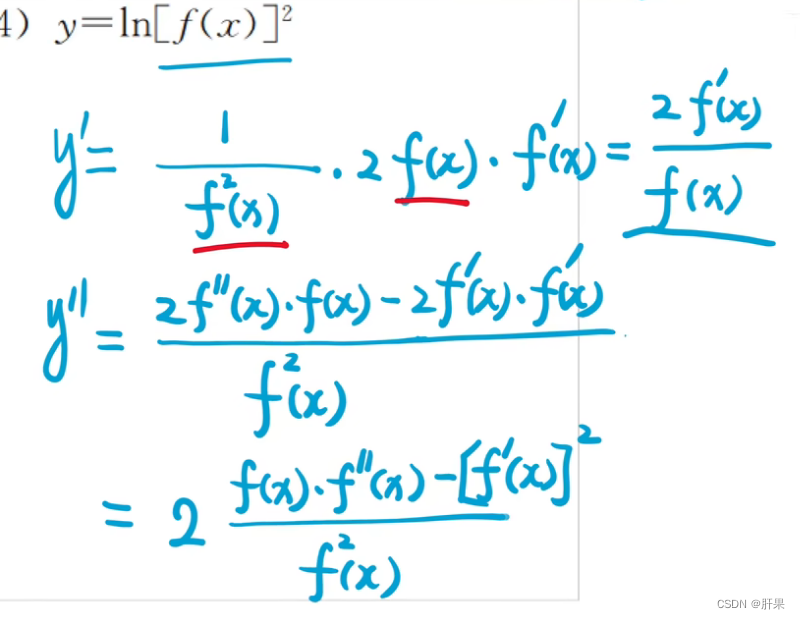
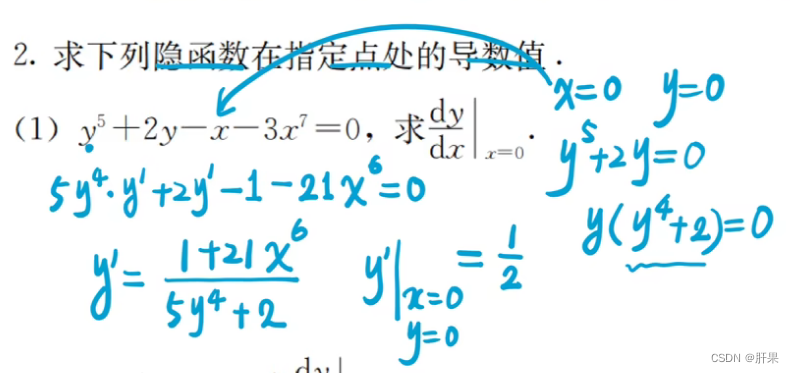
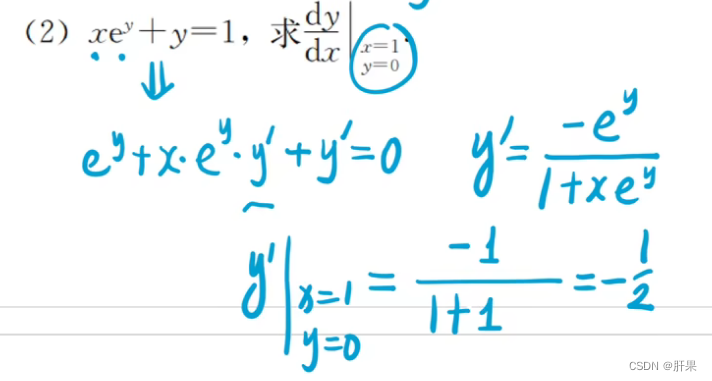
相关文章:
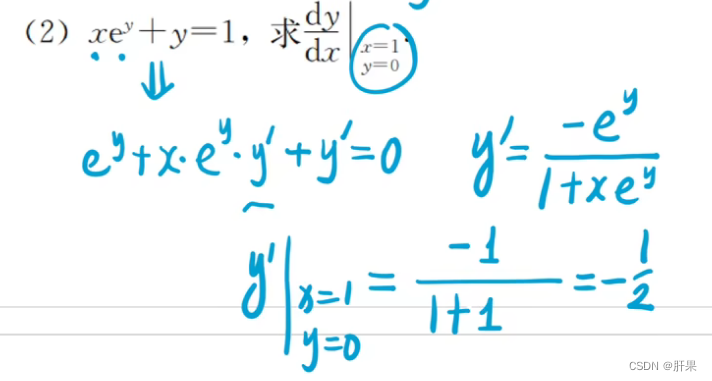
第六十八天学习记录:高等数学:导数(宋浩板书)
导数是微积分中的一个概念,描述了函数在某一个点上的变化率。具体地说,函数 f ( x ) f(x) f(x)在 x a xa xa处的导数为 f ′ ( a ) f(a) f′(a),表示当 x x x在 a a a处发生微小的变化 Δ x \Delta x Δx时, f ( x ) f(x) f(x)对…...
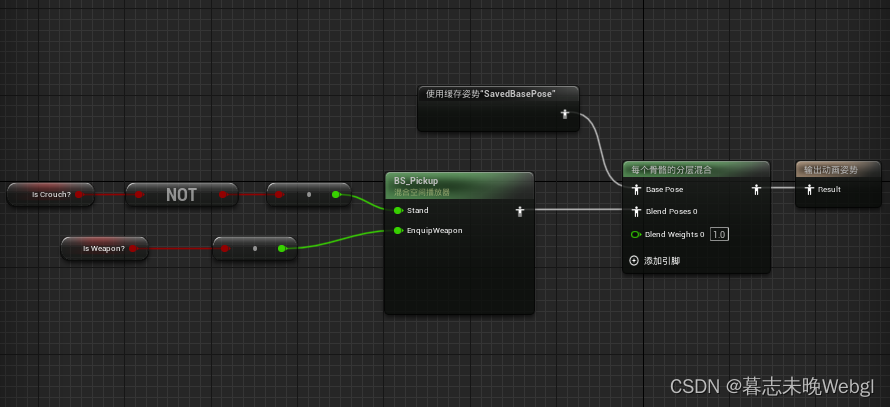
unreal 5 实现角色拾取功能
要实现角色拾取功能,我们需要实现蓝图接口功能,蓝图接口主要提供的是蓝图和蓝图之间可以通信,接下来,跟着教程,实现一下角色的拾取功能。 首先,我们要实现一个就是可视区的物品在朝向它的时候,会…...

chatgpt赋能python:如何使用Python升序排列一个列表?
如何使用Python升序排列一个列表? 在Python编程中,我们经常需要对列表进行排序。列表排序是一种常见的操作,可以帮助我们对数据进行分析和管理。在这篇文章中,我们将学习如何使用Python对一个列表进行升序排列。 什么是升序排列…...
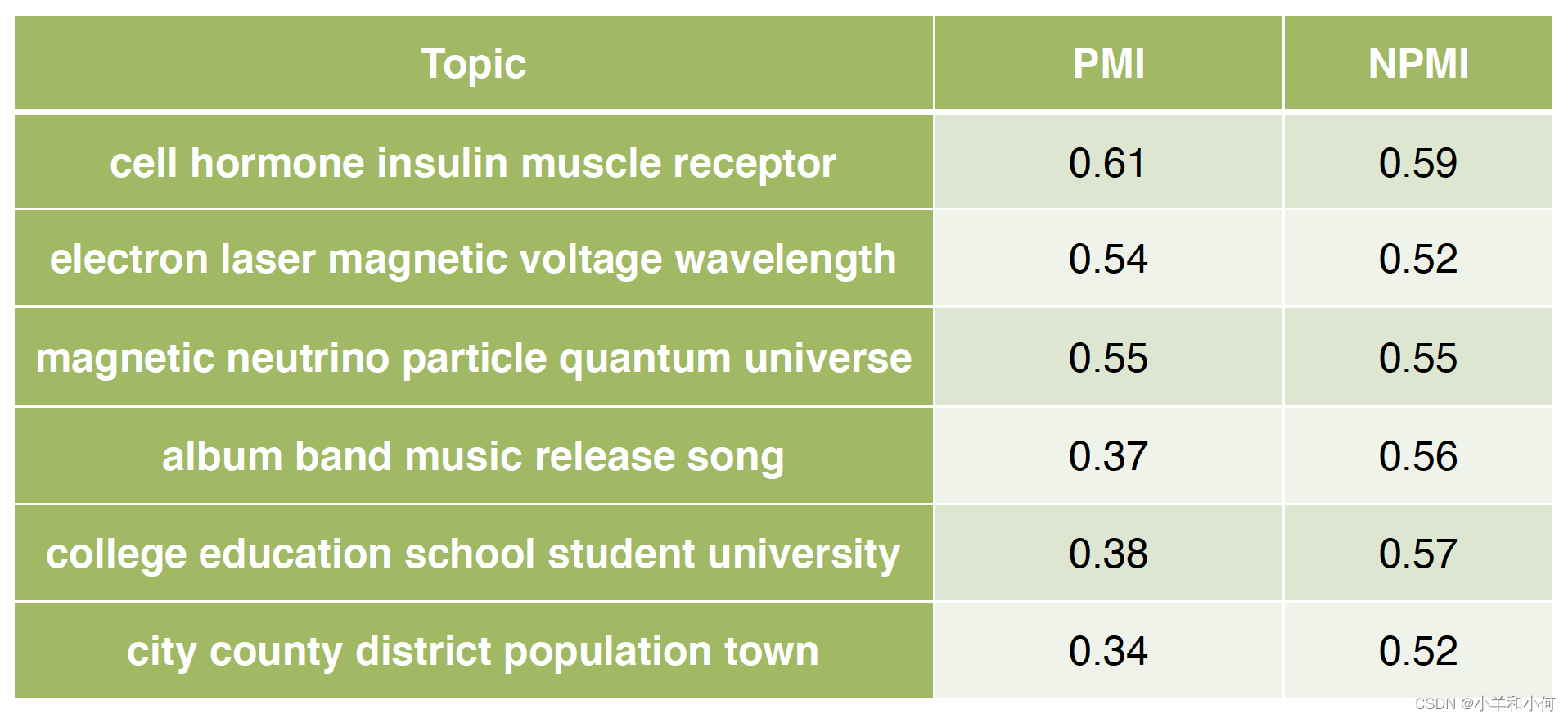
Lecture 20 Topic Modelling
目录 Topic ModellingA Brief History of Topic ModelsLDAEvaluationConclusion Topic Modelling makeingsense of text English Wikipedia: 6M articlesTwitter: 500M tweets per dayNew York Times: 15M articlesarXiv: 1M articlesWhat can we do if we want to learn somet…...

ThreadPoolExecutor线程池
文章目录 一、ThreadPool线程池状态二、ThreadPoolExecutor构造方法三、Executors3.1 固定大小线程池3.2 带缓冲线程池3.3 单线程线程池 四、ThreadPoolExecutor4.1 execute(Runnable task)方法使用4.2 submit()方法4.3 invokeAll()4.4 invokeAny()4.5 shutdown()4.6 shutdownN…...

chatgpt赋能python:Python实践:如何升级pip
Python实践:如何升级pip Python作为一门高效的脚本语言,被广泛应用于数据分析、人工智能、Web开发等领域。而pip则是Python的包管理工具,是开发Python应用的必备工具。但是pip在使用过程中,有时候会出现版本不兼容或者出现漏洞等…...
【JavaEE进阶】mybatis
目录: 一、Mybatis是什么 三个映射关系如下图: 二、mybatis的使用(前置工作简单案例) 第一步:导入MAVEN依赖 第二步: 在spring项目当中新建数据源 第三步:新建一个实体类,是和…...
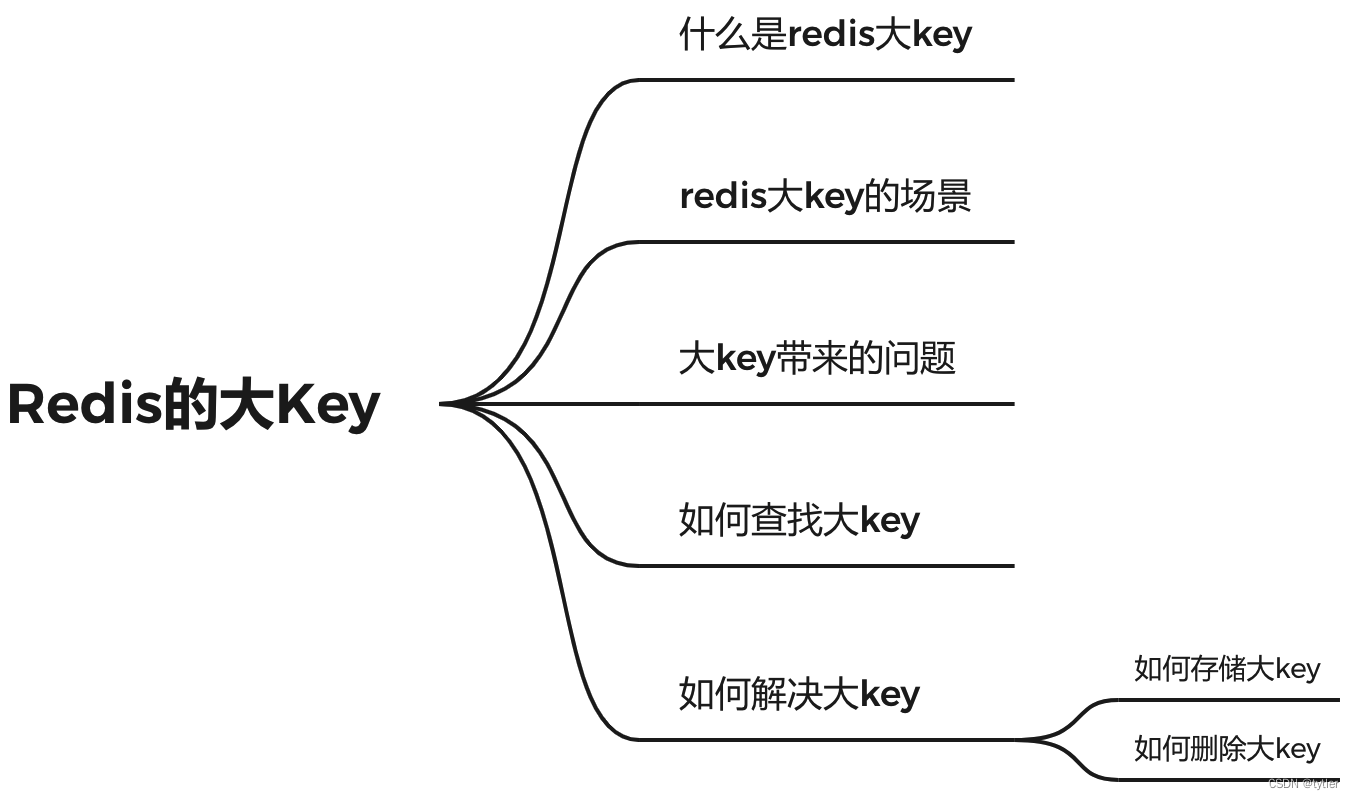
Redis的大key
什么是 redis 的大 key redis 的大 key 不是指存储在 redis 中的某个 key 的大小超过一定的阈值,而是该 key 所对应的 value 过大对于 string 类型来说,一般情况下超过 10KB 则认为是大 key;对于set、zset、hash 等类型来说,一般…...
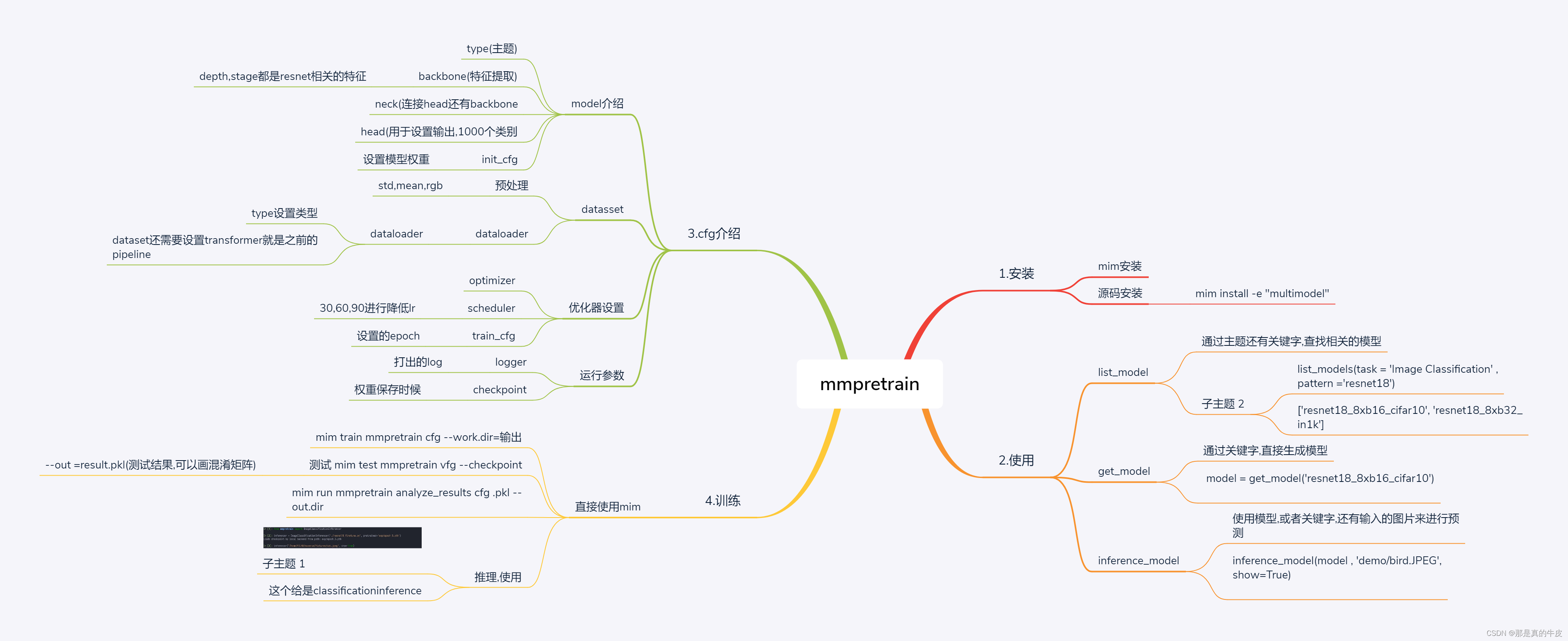
MMPretrain
title: mmpretrain实战 date: 2023-06-07 16:04:01 tags: [image classification,mmlab] mmpretrain实战 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ccTl9bOl-1686129437336)(null)] 主要讲解了安装,还有使用教程.安装教程直接参考官网.下面讲…...
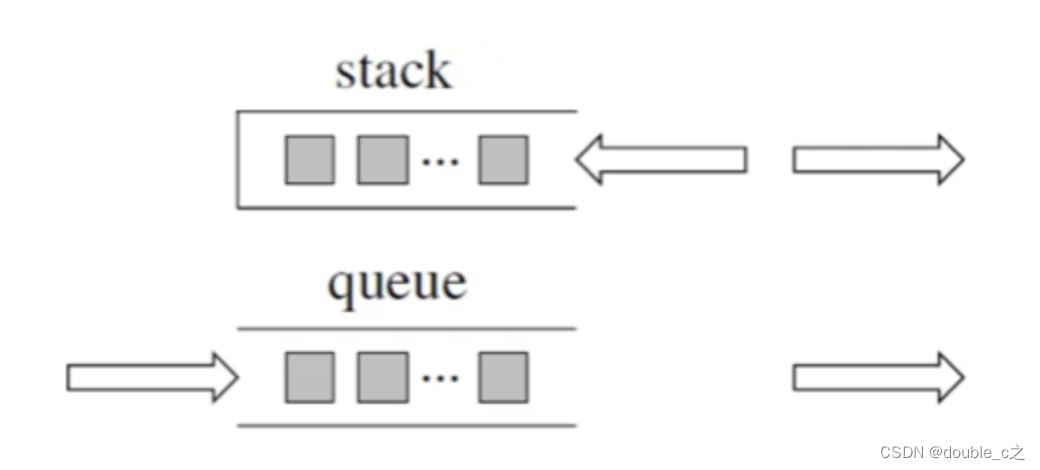
栈和队列(数据结构刷题)[一]-python
文章目录 前言一、原理介绍二、用栈实现队列1.操作2.思路 三、关于面试考察栈里面的元素在内存中是连续分布的么? 前言 提到栈和队列,大家可能对它们的了解只停留在表面,再深入一点,好像知道又好像不知道的感觉。本文我将从底层实…...

【备战秋招】JAVA集合
集合 前言 一方面, 面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象 的操作,就要 对对象进行存储。 另一方面,使用Array存储对象方面具有一些弊端,而Java 集合就像一种容器,可以动态地把多…...

setState详解
this. setState( [partialState], [callback]) 1.[partialState] :支持部分状态更改 this, setState({ x:100 //不论总共有多少状态,我们只修改了x,其余的状态不动 });callback :在状态更改/视图更新完毕后触发执行,也可以说只要执行了setS…...

Qt5.12.6配置Android Arm开发环境(windows)
1. 安装jdk1.8 2.安装Android Studio 并安装 SDK 与NDK SDK Tools 选择 26.0.3 SDK Platform 选择 Android SDK Platform 26 NDK选择19版本 安卓ARM环境配置成功如下: JDK1.8 , SDK 26 , NDK 19 在安装QT时要选择 ARMv7(32位CPU)与ARM64-v8a(64位CPU) 选择支持android平台…...
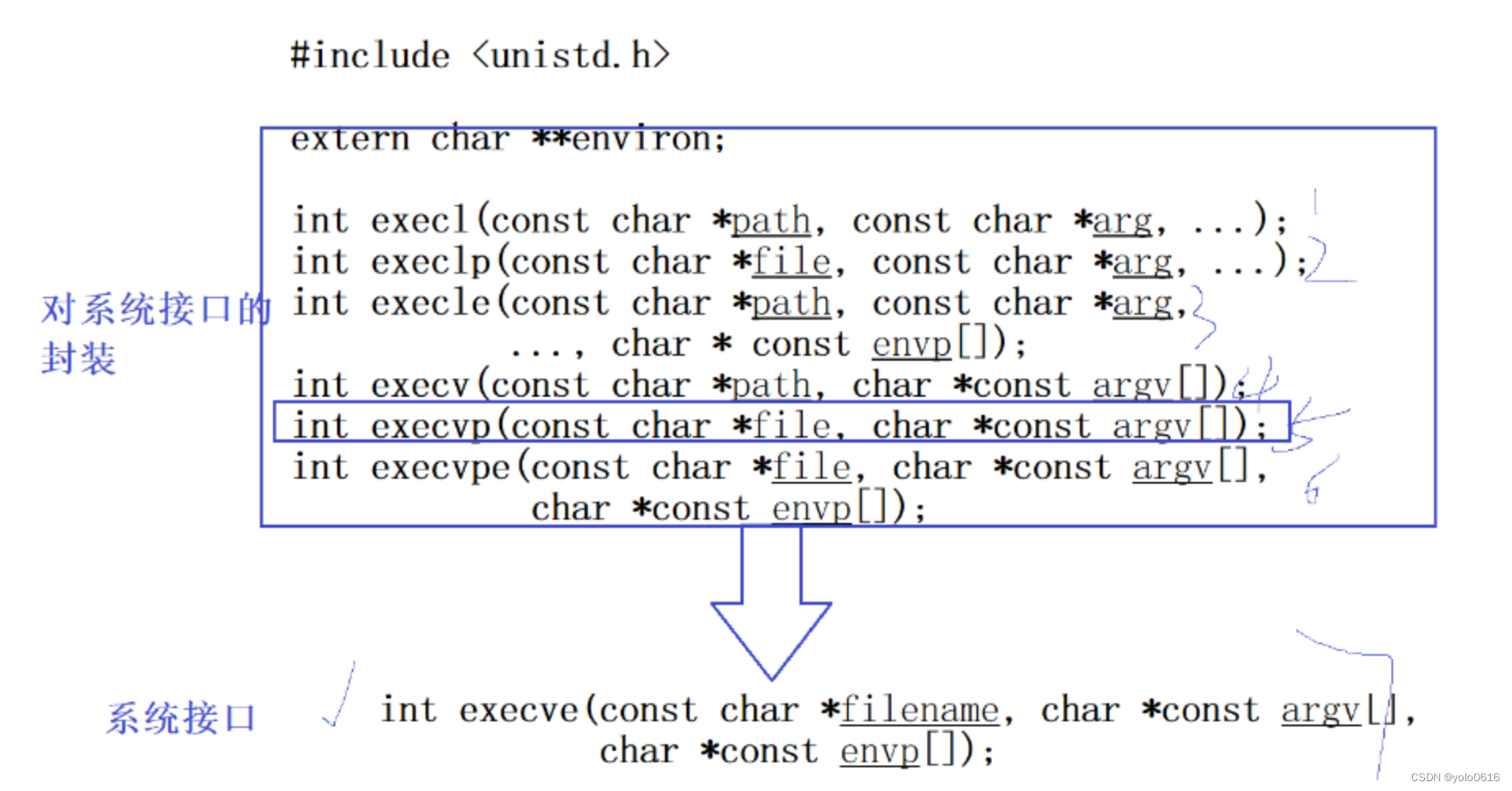
七、进程程序替换
文章目录 一、进程程序替换(一)概念(二)为什么程序替换(三)程序替换的原理(四)如何进行程序替换1. execl2. 引入进程创建——子进程执行程序替换,会不会影响父进程呢? &…...
C++核心编程——详解运算符重载
文章目录💬 一.运算符重载基础知识①基本概念②运算符重载的规则③运算符重载形式④运算符重载建议 二.常用运算符重载①左移(<<)和右移(>>)运算符重载1️⃣重载后函数参数是什么?2️⃣重载的函数返回类型是什么?3️⃣重载为哪种…...
2023年前端面试汇总-CSS
1. CSS基础 1.1. CSS选择器及其优先级 对于选择器的优先级: 1. 标签选择器、伪元素选择器:1; 2. 类选择器、伪类选择器、属性选择器:10; 3. id 选择器:100; 4. 内联样式:1000&a…...

Java调用Pytorch实现以图搜图(附源码)
Java调用Pytorch实现以图搜图 设计技术栈: 1、ElasticSearch环境; 2、Python运行环境(如果事先没有pytorch模型时,可以用python脚本创建模型); 1、运行效果 2、创建模型(有则可以跳过…...
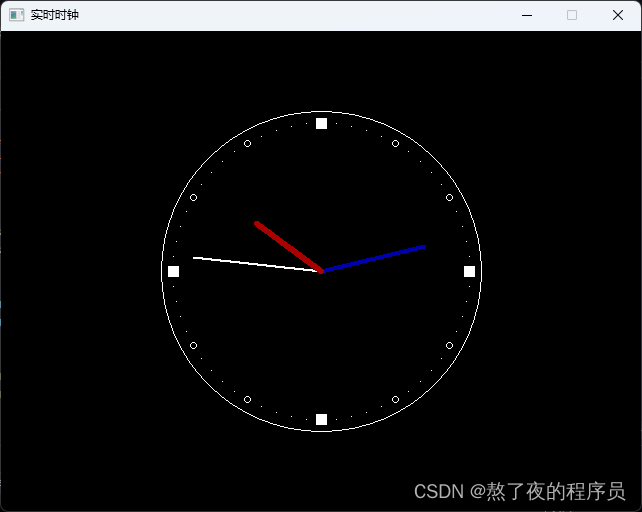
【EasyX】实时时钟
目录 实时时钟1. 绘制静态秒针2. 秒针的转动3. 根据实际时间转动4. 添加时针和分针5. 添加表盘刻度 实时时钟 本博客介绍利用EasyX实现一个实时钟表的小程序,同时学习时间函数的使用。 本文源码可从github获取 1. 绘制静态秒针 第一步定义钟表的中心坐标center&a…...

基于XC7Z100的PCIe采集卡(GMSL FMC采集卡)
GMSL 图像采集卡 特性 ● PCIe Gen2.0 X8 总线; ● 支持V4L2调用; ● 1路CAN接口; ● 6路/12路 GMSL1/2摄像头输入,最高可达8MP; ● 2路可定义相机同步触发输入/输出; 优势 ● 采用PCIe主卡与FMC子…...
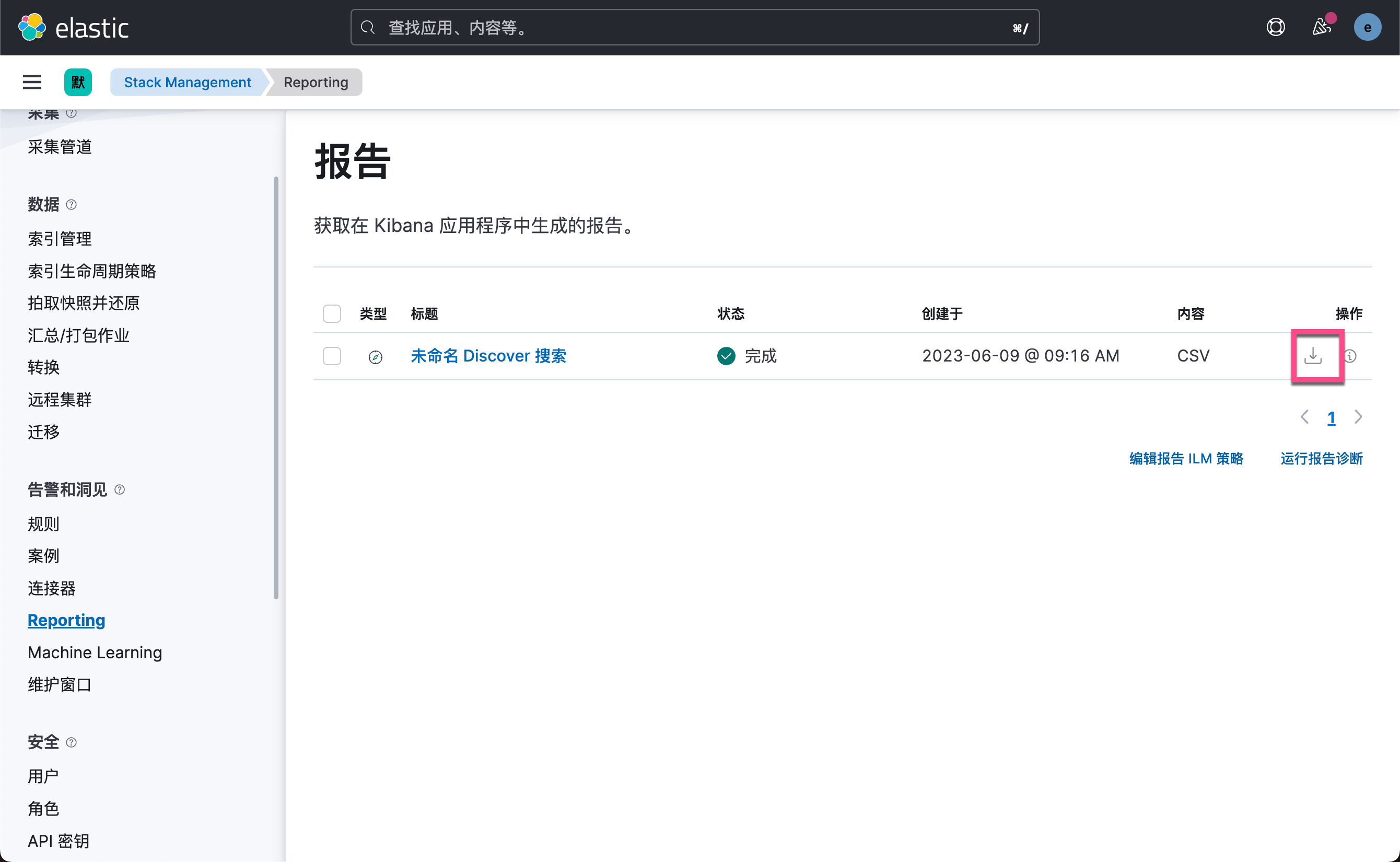
Kibana:使用 Kibana 自带数据进行可视化(一)
在今天的练习中,我们将使用 Kibana 自带的数据来进行一些可视化的展示。希望对刚开始使用 Kibana 的用户有所帮助。 前提条件 如果你还没有安装好自己的 Elastic Stack,你可以参考如下的视频来开启 Elastic Stack 并进行下面的练习。你可以开通阿里云检…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
