19 贝叶斯线性回归
文章目录
- 19 贝叶斯线性回归
- 19.1 频率派线性回归
- 19.2 Bayesian Method
- 19.2.1 Inference问题
- 19.2.2 Prediction问题
19 贝叶斯线性回归
19.1 频率派线性回归
数据与模型:
-
样本:
{ ( x i , y i ) } i = 1 N , x i ∈ R p , y i ∈ R p {\lbrace (x_i, y_i) \rbrace}_{i=1}^{N}, \quad x_i \in {\mathbb R}^p, \quad y_i \in {\mathbb R}^p {(xi,yi)}i=1N,xi∈Rp,yi∈RpX = ( x 1 x 2 … x N ) T = ( x 1 T x 2 T … x N T ) = ( x 11 x 12 … x 1 N x 21 x 22 … x 2 N … x N 1 x N 2 … x N N ) , Y = ( y 1 T y 2 T … y N T ) X = (x_1 \ x_2 \ \dots \ x_N )^T = \begin{pmatrix} x_1^T \\ x_2^T \\ \dots \\ x_N^T \end{pmatrix} = \begin{pmatrix} x_{11} & x_{12} & \dots & x_{1N} \\ x_{21} & x_{22} & \dots & x_{2N} \\ \dots \\ x_{N1} & x_{N2} & \dots & x_{NN} \\ \end{pmatrix} , Y = \begin{pmatrix} y_1^T \\ y_2^T \\ \dots \\ y_N^T \end{pmatrix} X=(x1 x2 … xN)T= x1Tx2T…xNT = x11x21…xN1x12x22xN2………x1Nx2NxNN ,Y= y1Ty2T…yNT
-
回归方程:
f ( x ) = w T x = x T w , y = f ( x ) + ε ⏟ n o i s e , ε ∽ N ( 0 , σ 2 ) f(x) = w^T x = x^T w, \quad y = f(x) + \underbrace{\varepsilon}_{noise}, \quad \varepsilon \backsim N(0,\sigma^2) f(x)=wTx=xTw,y=f(x)+noise ε,ε∽N(0,σ2)
其中 x , y , ε x, y, \varepsilon x,y,ε都是随机变量,假设 w w w用于表示参数
在频率派的线性回归中,我们是通过假设 w w w表示一个未知的常量,转化为优化问题进行求解。我们将这种方法称为点估计,在过去我们学习过了两种方法:
-
L S E ⟸ M L E ( noise is Gaussian ) LSE \impliedby MLE(\text{noise is Gaussian}) LSE⟸MLE(noise is Gaussian)——极大似然估计:
w M L E = a r g max w P ( D a t a ∣ w ) w_{MLE} = arg\max_{w} P(Data|w) wMLE=argwmaxP(Data∣w) -
R e g u l a r i z e d L S E ⟸ M A P ( noise is Gaussian ) Regularized \ LSE \impliedby MAP(\text{noise is Gaussian}) Regularized LSE⟸MAP(noise is Gaussian)——最大后验估计:
w M A P = a r g max w P ( w ∣ D a t a ) ⏟ ∝ P ( D a t a ∣ w ) ⋅ P ( w ) = a r g max w P ( D a t a ∣ w ) ⋅ P ( w ) w_{MAP} = arg\max_{w} \underbrace{P(w|Data)}_{\propto P(Data|w) \cdot P(w)} = arg\max_{w} P(Data|w) \cdot P(w) wMAP=argwmax∝P(Data∣w)⋅P(w) P(w∣Data)=argwmaxP(Data∣w)⋅P(w)
其中若 P ( w ) P(w) P(w)表示为Gaussian Dist则为岭回归(Ridge),若 P ( w ) P(w) P(w)表示为Laplace则为Lasso
在本章我们的目标是通过Bayesian Method解决线性回归问题:
- 假定 w w w是一个随机变量
- 求出后验 P ( w ∣ D a t a ) P(w|Data) P(w∣Data)
19.2 Bayesian Method
数据与模型:
-
样本数据:
{ ( x i , y i ) } i = 1 N , x i ∈ R p , y i ∈ R p {\lbrace (x_i, y_i) \rbrace}_{i=1}^{N}, \quad x_i \in {\mathbb R}^p, \quad y_i \in {\mathbb R}^p {(xi,yi)}i=1N,xi∈Rp,yi∈RpX = ( x 1 x 2 … x N ) T = ( x 1 T x 2 T … x N T ) = ( x 11 x 12 … x 1 N x 21 x 22 … x 2 N … x N 1 x N 2 … x N N ) , Y = ( y 1 T y 2 T … y N T ) X = (x_1 \ x_2 \ \dots \ x_N )^T = \begin{pmatrix} x_1^T \\ x_2^T \\ \dots \\ x_N^T \end{pmatrix} = \begin{pmatrix} x_{11} & x_{12} & \dots & x_{1N} \\ x_{21} & x_{22} & \dots & x_{2N} \\ \dots \\ x_{N1} & x_{N2} & \dots & x_{NN} \\ \end{pmatrix} , Y = \begin{pmatrix} y_1^T \\ y_2^T \\ \dots \\ y_N^T \end{pmatrix} X=(x1 x2 … xN)T= x1Tx2T…xNT = x11x21…xN1x12x22xN2………x1Nx2NxNN ,Y= y1Ty2T…yNT
-
模型:
f ( x ) = w T x = x T w , y = f ( x ) + ε ⏟ n o i s e , ε ∽ N ( 0 , σ 2 ) f(x) = w^T x = x^T w, \quad y = f(x) + \underbrace{\varepsilon}_{noise}, \quad \varepsilon \backsim N(0,\sigma^2) f(x)=wTx=xTw,y=f(x)+noise ε,ε∽N(0,σ2)
其中 x , y , ε , w x, y, \varepsilon, w x,y,ε,w都是随机变量,假设用于表示参数 -
问题表示:
{ I n f e r e n c e : p o s t e r i o r ( w ) P r e d i c t i o n : x ∗ → y ∗ \begin{cases} Inference: posterior(w) \\ Prediction: x^* \rightarrow y^* \end{cases} {Inference:posterior(w)Prediction:x∗→y∗
19.2.1 Inference问题
Inference问题就是求解后验: P ( w ∣ D a t a ) P(w|Data) P(w∣Data)。接下来进行逐步的推导:
P ( w ∣ D a t a ) = P ( w ∣ X , Y ) = P ( w , Y ∣ X ) P ( Y ∣ X ) = P ( Y ∣ w , X ) ⏞ l i k e l i h o o d ⋅ P ( w ∣ X ) ⏞ p r i o r ∫ P ( Y ∣ w , X ) ⋅ P ( w ∣ X ) d w \begin{align} P(w|Data) = P(w|X, Y) = \frac{P(w, Y| X)}{P(Y|X)} = \frac{\overbrace{P(Y|w, X)}^{likelihood} \cdot \overbrace{P(w|X)}^{prior}}{\int P(Y|w, X) \cdot P(w|X) {\rm d}w} \end{align} P(w∣Data)=P(w∣X,Y)=P(Y∣X)P(w,Y∣X)=∫P(Y∣w,X)⋅P(w∣X)dwP(Y∣w,X) likelihood⋅P(w∣X) prior
将后验拆解开之后,我们只需要分开求解likelihood和prior:
-
求解likelihood:
P ( Y ∣ w , X ) = ∏ i = 1 N P ( y i ∣ w , x i ) = ∏ i = 1 N N ( y i ∣ w T x i , σ 2 ) P(Y|w, X) = \prod_{i=1}^{N} P(y_i| w, x_i) = \prod_{i=1}^{N} N(y_i| w^T x_i, \sigma^2) P(Y∣w,X)=i=1∏NP(yi∣w,xi)=i=1∏NN(yi∣wTxi,σ2) -
假设prior:
p ( w ∣ X ) = N ( 0 , Σ p ) p(w|X) = N(0, \Sigma_p) p(w∣X)=N(0,Σp)
所以求解后验可以写为:
P ( w ∣ D a t a ) ∝ P ( Y ∣ w , X ) ⋅ P ( w ∣ X ) ∝ ∏ i = 1 N N ( y i ∣ w T x i , σ 2 ) ⋅ N ( 0 , Σ p ) \begin{align} P(w|Data) &\propto P(Y|w,X) \cdot P(w|X) \\ &\propto \prod_{i=1}^{N} N(y_i| w^T x_i, \sigma^2) \cdot N(0, \Sigma_p) \end{align} P(w∣Data)∝P(Y∣w,X)⋅P(w∣X)∝i=1∏NN(yi∣wTxi,σ2)⋅N(0,Σp)
我们先将likelihood进行一个变换:
P ( Y ∣ w , X ) = ∏ i = 1 N N ( y i ∣ w T x i , σ 2 ) = ∏ i = 1 N 1 ( 2 π ) 1 2 σ exp { − 1 2 σ 2 ( y i − w T x i ) 2 } = 1 ( 2 π ) N 2 σ N exp { − 1 2 σ 2 ∑ i = 1 N ( y i − w T x i ) 2 } = 1 ( 2 π ) N 2 σ N ⏟ ∣ Σ ∣ 1 2 exp { − 1 2 ( Y − X w ) ⏟ x − μ T σ − 2 I ⏟ Σ − 1 ( Y − X w ) } = N ( X w , σ − 2 I ) \begin{align} P(Y|w, X) &= \prod_{i=1}^{N} N(y_i| w^T x_i, \sigma^2) \\ &= \prod_{i=1}^{N} \frac{ 1 }{ {(2 \pi)}^\frac{1}{2} \sigma } \exp{\lbrace -\frac{1}{2\sigma^2} {( y_i - w^T x_i )}^2 \rbrace} \\ &= \frac{ 1 }{ {(2 \pi)}^\frac{N}{2} \sigma^N } \exp{\lbrace -\frac{1}{2\sigma^2} \sum_{i=1}^N {( y_i - w^T x_i )}^2 \rbrace} \\ &= \frac{ 1 }{ {(2 \pi)}^\frac{N}{2} \underbrace{\sigma^N}_{{|\Sigma|}^\frac{1}{2}} } \exp{\lbrace -\frac{1}{2} {\underbrace{(Y-Xw)}_{x-\mu}}^T \underbrace{\sigma^{-2} I}_{\Sigma^{-1}} {(Y-Xw)} \rbrace} \\ &= N(Xw, \sigma^{-2} I) \end{align} P(Y∣w,X)=i=1∏NN(yi∣wTxi,σ2)=i=1∏N(2π)21σ1exp{−2σ21(yi−wTxi)2}=(2π)2NσN1exp{−2σ21i=1∑N(yi−wTxi)2}=(2π)2N∣Σ∣21 σN1exp{−21x−μ (Y−Xw)TΣ−1 σ−2I(Y−Xw)}=N(Xw,σ−2I)
通过上文的likelihood我们可以求解:
P ( w ∣ D a t a ) ∝ P ( Y ∣ w , X ) ⋅ P ( w ∣ X ) = N ( X w , σ − 2 I ) ) ⋅ N ( 0 , Σ p ) ∝ exp { − 1 2 ( Y − X w ) T σ − 2 I ( Y − X w ) } ⋅ exp { − 1 2 w T Σ p − 1 w } = exp { − 1 2 ( Y − X w ) T σ − 2 I ( Y − X w ) − 1 2 w T Σ p − 1 w } = exp { − 1 2 ( Y T Y − 2 Y T X w + w T X T X w ) − 1 2 w T Σ p − 1 w } \begin{align} P(w|Data) &\propto P(Y|w,X) \cdot P(w|X) = N(Xw, \sigma^{-2} I)) \cdot N(0, \Sigma_p) \\ &\propto \exp{\lbrace -\frac{1}{2} {{(Y-Xw)}}^T {\sigma^{-2} I} {(Y-Xw)} \rbrace} \cdot \exp{\lbrace -\frac{1}{2} w^T \Sigma_p^{-1} w \rbrace} \\ &= \exp{\lbrace -\frac{1}{2} {{(Y-Xw)}}^T {\sigma^{-2} I} {(Y-Xw)} -\frac{1}{2} w^T \Sigma_p^{-1} w \rbrace} \\ &= \exp{\lbrace -\frac{1}{2} {( Y^T Y - 2Y^T X w + w^T X^T X w )} -\frac{1}{2} w^T \Sigma_p^{-1} w \rbrace} \\ \end{align} P(w∣Data)∝P(Y∣w,X)⋅P(w∣X)=N(Xw,σ−2I))⋅N(0,Σp)∝exp{−21(Y−Xw)Tσ−2I(Y−Xw)}⋅exp{−21wTΣp−1w}=exp{−21(Y−Xw)Tσ−2I(Y−Xw)−21wTΣp−1w}=exp{−21(YTY−2YTXw+wTXTXw)−21wTΣp−1w}
引入配方法:
若将标准的高斯分布可以得到二次项和一次项:
p ( x ) ∝ exp { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } = exp { − 1 2 ( x T Σ − 1 x − x T Σ − 1 μ ⏟ 1 × 1 − μ T Σ − 1 x ⏟ 1 × 1 + μ T Σ − 1 μ ) } = exp { − 1 2 ( x T Σ − 1 x − 2 μ T Σ − 1 x + μ T Σ − 1 μ ⏟ 与 x 无关 ) } ∝ exp { − 1 2 x T Σ − 1 x ⏟ 二次项 − μ T Σ − 1 x ⏟ 一次项 } \begin{align} p(x) &\propto \exp{\lbrace -\frac{1}{2}{(x-\mu)}^T \Sigma^{-1} (x-\mu) \rbrace} \\ &= \exp{\lbrace -\frac{1}{2} (x^T \Sigma^{-1} x - \underbrace{x^T \Sigma^{-1} \mu}_{1 \times 1} - \underbrace{\mu^T \Sigma^{-1} x}_{1 \times 1} + \mu^T \Sigma^{-1} \mu) \rbrace} \\ &= \exp{\lbrace -\frac{1}{2} (x^T \Sigma^{-1} x - 2 \mu^T \Sigma^{-1} x + \underbrace{\mu^T \Sigma^{-1} \mu}_{与x无关}) \rbrace} \\ &\propto \exp{\lbrace \underbrace{-\frac{1}{2} x^T \Sigma^{-1} x}_{二次项} - \underbrace{\mu^T \Sigma^{-1} x}_{一次项} \rbrace} \\ \end{align} p(x)∝exp{−21(x−μ)TΣ−1(x−μ)}=exp{−21(xTΣ−1x−1×1 xTΣ−1μ−1×1 μTΣ−1x+μTΣ−1μ)}=exp{−21(xTΣ−1x−2μTΣ−1x+与x无关 μTΣ−1μ)}∝exp{二次项 −21xTΣ−1x−一次项 μTΣ−1x}
我们可以通过二次项和一次项求出均值和方差
让我们用配方法,取出 P ( w ∣ D a t a ) P(w|Data) P(w∣Data)的二次项和一次项,假设 P ( w ∣ D a t a ) P(w|Data) P(w∣Data)的均值和方差表示为 μ w , Σ w \mu_w, \Sigma_w μw,Σw:
{ 二次项: − 1 2 σ 2 w T X T X w − 1 2 w T Σ p − 1 w = − 1 2 ( w T ( σ − 2 X T X + Σ p − 1 ) w ) ⏟ − 1 2 x T Σ w − 1 x 一次项: σ − 2 Y T X w ⏟ μ T Σ w − 1 x ⟹ { Σ w − 1 = ( σ − 2 X T X + Σ p − 1 ) μ T Σ w − 1 = σ − 2 Y T X \begin{align} &\begin{cases} \text{二次项:} -\frac{1}{2 \sigma^2} w^T X^T X w - \frac{1}{2} w^T \Sigma_p^{-1} w = \underbrace{ -\frac{1}{2} {(w^T {(\sigma^{-2} X^T X + \Sigma_p^{-1})} w)}}_{-\frac{1}{2} x^T \Sigma_w^{-1} x} \\ \text{一次项:} \underbrace{\sigma^{-2} Y^T X w}_{\mu^T \Sigma_w^{-1} x} \end{cases} \\ \implies &\begin{cases} \Sigma_w^{-1} = {(\sigma^{-2} X^T X + \Sigma_p^{-1})} \\ \mu^T \Sigma_w^{-1} = \sigma^{-2} Y^T X \end{cases} \end{align} ⟹⎩ ⎨ ⎧二次项:−2σ21wTXTXw−21wTΣp−1w=−21xTΣw−1x −21(wT(σ−2XTX+Σp−1)w)一次项:μTΣw−1x σ−2YTXw{Σw−1=(σ−2XTX+Σp−1)μTΣw−1=σ−2YTX
通过上文的方程可以简单求解出均值和方差:
{ Σ w = ( σ − 2 X T X + Σ p − 1 ) − 1 μ T = σ − 4 X T X Y T X + σ − 2 Σ p − 1 Y T X \begin{cases} \Sigma_w = {(\sigma^{-2} X^T X + \Sigma_p^{-1})}^{-1} \\ \mu^T = \sigma^{-4} X^T X Y^T X + \sigma^{-2} \Sigma_p^{-1} Y^T X \end{cases} {Σw=(σ−2XTX+Σp−1)−1μT=σ−4XTXYTX+σ−2Σp−1YTX
19.2.2 Prediction问题
Prediction问题是假设已有数据为 x ∗ x^* x∗,要求在 y ∗ y^* y∗的条件下的概率分布。
我们的条件有:
{ f ( x ) = x T w w ∽ N ( μ w , Σ w ) \begin{cases} f(x) = x^T w \\ w \backsim N(\mu_w, \Sigma_w) \end{cases} {f(x)=xTww∽N(μw,Σw)
此时我们已知 f ( x ∗ ) = x ∗ T w f(x^*) = {x^*}^T w f(x∗)=x∗Tw,可以根据参数的分布得到 P ( x ∗ T w ) P({x^*}^T w) P(x∗Tw):
w ∽ N ( μ w , Σ w ) ⟹ x ∗ T w ∽ N ( x ∗ T μ w , x ∗ T Σ w x ∗ ) \begin{align} & w \backsim N(\mu_w, \Sigma_w) \\ \implies & {x^*}^T w \backsim N({x^*}^T \mu_w, {x^*}^T \Sigma_w x^*) \end{align} ⟹w∽N(μw,Σw)x∗Tw∽N(x∗Tμw,x∗TΣwx∗)
实际情况是我们要求解 y = f ( x ∗ ) + ε , ε ∽ N ( 0 , σ 2 ) y = f(x^*) + \varepsilon, \quad \varepsilon \backsim N(0, \sigma^2) y=f(x∗)+ε,ε∽N(0,σ2),也就是求解分布 P ( y ∗ ∣ D a t a , x ∗ ) P(y^*| Data, x^*) P(y∗∣Data,x∗):
{ y = x ∗ T w + ε , ε ∽ N ( 0 , σ 2 ) x ∗ T w ∽ N ( x ∗ T μ w , x ∗ T Σ w x ∗ ) ⟹ P ( y ∗ ∣ D a t a , x ∗ ) = N ( x ∗ T μ w , x ∗ T Σ w x ∗ + σ 2 ) \begin{align} &\begin{cases} y = {x^*}^T w + \varepsilon, \quad \varepsilon \backsim N(0, \sigma^2) \\ {x^*}^T w \backsim N({x^*}^T \mu_w, {x^*}^T \Sigma_w x^*) \end{cases} \\ \implies & P(y^*|Data, x^*) = N({x^*}^T \mu_w, {x^*}^T \Sigma_w x^* + \sigma^2) \end{align} ⟹{y=x∗Tw+ε,ε∽N(0,σ2)x∗Tw∽N(x∗Tμw,x∗TΣwx∗)P(y∗∣Data,x∗)=N(x∗Tμw,x∗TΣwx∗+σ2)
相关文章:

19 贝叶斯线性回归
文章目录 19 贝叶斯线性回归19.1 频率派线性回归19.2 Bayesian Method19.2.1 Inference问题19.2.2 Prediction问题 19 贝叶斯线性回归 19.1 频率派线性回归 数据与模型: 样本: { ( x i , y i ) } i 1 N , x i ∈ R p , y i ∈ R p {\lbrace (x_i, y_…...
第七十天学习记录:高等数学:微分(宋浩板书)
微分的定义 基本微分公式与法则 复合函数的微分 微分的几何意义 微分在近似计算中应用 sin(xy) sin(x)cos(y) cos(x)sin(y)可以用三角形的几何图形来进行证明。 假设在一个单位圆上,点A(x,y)的坐标为(x,y),点B(x’, y’)的坐标为(x’, y’)。则以两点…...

Jmeter
目录 一、jmeter 安装 二、jmeter 介绍 1、jmeter是什么? 2、jmeter 用来做什么? 3、优点 4、缺点 5、jmeter 目录介绍 ①_bin 目录介绍 ② docs 目录 — — 接口文档目录 ③ extras目录 — — 扩展插件目录 ④ lib 目录 — — 所用到的插件目录 ⑤ lic…...

Flutter 学习 之 时间转换工具类
Flutter 学习之时间转换工具类 在 Flutter 应用程序开发中,处理时间戳是非常常见的需求。我们通常需要将时间戳转换为人类可读的日期时间格式。为了实现这一点,我们可以创建一个时间转换工具类。 实现方法 以下是一个简单的时间转换工具类的示例&…...
docker consul
docker consul的容器服务更新与发现 服务注册与发现是微服务架构中不可或缺的重要组件,起始服务都是单节点的,不保障高可用性,也不考虑服务的承载压力,服务之间调用单纯的通过接口访问的,直到后来出现多个节点的分布式…...
全志V3S嵌入式驱动开发(开发环境再升级)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面我们陆陆续续开发了差不多有10个驱动,涉及到网口、串口、音频和视频等几个方面。但是整个开发的效率还是比较低的。每次开发调试的…...

ChatGPT:人工智能助手的新时代
ChatGPT:人工智能助手的新时代 文章目录 ChatGPT:人工智能助手的新时代引言ChatGPT的原理GPT-3.5架构概述预训练和微调过程生成式对话生成技术 ChatGPT的应用场景智能助理客服机器人虚拟角色教育辅助创意生成个性化推荐 ChatGPT的优势ChatGPT的使用技巧与…...

【面试】二、Java补充知识
JVM中的存储 JVM的五块存储区: 方法区(线程共享) 方法区用来存储类的各种信息(类名、方法信息等)、静态变量、常量和编译后的代码也存储在方法区中 方法区中也存在运行时常量池 常量池中会存放程序运行时生成的各种…...

LISTENER、TNSNAMES和SQLNET配置文件
LISTENER、TNSNAMES和SQLNET配置文件 用户连接验证listener.ora文件配置监听日志local_listener参数 tnsnames.ora文件配置 sqlnet.ora文件配置 用户连接验证 Oracle数据库中用户有三种常见的登录验证方式: 通过操作系统用户验证:必须是在数据库服务器…...
【Leetcode -225.用队列实现栈 -232.用栈实现队列】
Leetcode Leetcode -225.用队列实现栈Leetcode -232.用栈实现队列 Leetcode -225.用队列实现栈 题目:仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 …...
悟道3.0全面开源!LeCun VS Max 智源大会最新演讲
夕小瑶科技说 原创 作者 | 小戏 2023 年智源大会如期召开! 这场汇集了 Geoffery Hinton、Yann LeCun、姚期智、Joseph Sifakis、Sam Altman、Russell 等一众几乎是 AI 领域学界业界“半壁江山”的大佬们的学术盛会,聚焦 AI 领域的前沿问题,…...
2023蓝桥杯大学A组C++决赛游记+个人题解
Day0 发烧了一晚上没睡着,感觉鼻子被打火机烧烤一样难受,心情烦躁 早上6点起来吃了个早饭,思考能力完全丧失了,开始看此花亭奇谭 看了六集,准备复习数据结构考试,然后秒睡 一睁眼就是下午2点了 挂了个…...

wkhtmltopdf踩坑记录
1. 不支持writing-mode。 需求是文字纵向排列,内容从左到右,本来用的是writing-mode: tb-rl;,插件转pdf后发现失效。 解决方法: 让每一列文字单独用一个div容器包裹,对它的宽度进行限制,控制每一行只能出现…...

贪心算法part2 | ● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II
文章目录 122.买卖股票的最佳时机II思路思路代码官方题解困难 55. 跳跃游戏思路思路代码官方题解代码困难 45.跳跃游戏II思路思路代码困难 今日收获 122.买卖股票的最佳时机II 122.买卖股票的最佳时机II 思路 局部最优:将当天价格和前一天比较,价格涨…...

[C++]异常笔记
我不怕练过一万种腿法的对手,就怕将一种腿法 练一万次的对手。 什么是C的异常 在C中,异常处理通常使用try-catch块来实现。try块用于包含可能会抛出异常的代码,而catch块用于捕获并处理异常。当异常被抛出时,程序会跳过try块中未执行…...

浅谈一级机电管道设计中的压力与介质温度
管道设计是工程设计中的一个非常重要的部分,管道的设计需要考虑到许多因素,其中就包括管道设计压力分类和介质温度分类。这两个因素是在设计管道时必须非常严格考虑的, 首先是管道设计压力分类。在管道设计中,根据工作要求和要传输…...
使用 macvlan 网络)
Docker网络模型(八)使用 macvlan 网络
使用 macvlan 网络 一些应用程序,特别是传统的应用程序或监控网络流量的应用程序,期望直接连接到物理网络。在这种情况下,你可以使用 macvlan 网络驱动为每个容器的虚拟网络接口分配一个MAC地址,使其看起来像一个直接连接到物理网…...
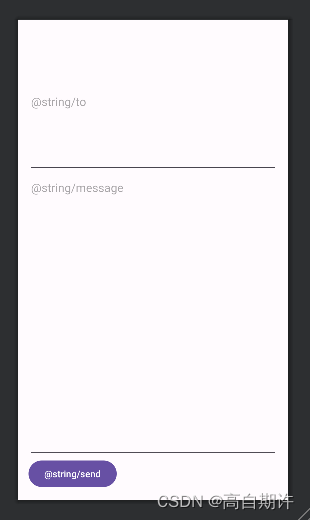
控制视图内容的位置
文本域中的提示内容在默认情况下是垂直居中的,要改变文本在文本域中的位置,可以使用android:gravity来实现。 利用android:gravity可以指定如何在视图中放置视图内容,例如,如何在文本域中放置文本。 如果希望视图文本显示在上方&a…...

【分布式系统与一致性协议】
分布式系统与一致性协议 CAP原理APCPCA总结BASE理论 一致性拜占庭将军问题 分布式系统是一个硬件或软件组件分布在不同的网络计算机上,彼此之间仅仅通过消息传递进行通信和协调的系统。 分布式系统的设计目标一般包含如下: 可用性:可用性是分…...

音视频领域的未来发展方向展望
文章目录 音视频领域的未来发展方向全景音视频技术虚拟现实和增强现实的区别 人工智能技术可视化智能分析智能语音交互图像识别和视频分析技术 语音处理智能推荐技术远程实时通信 流媒体技术未来方向 音视频领域的未来发展方向 全景音视频技术:全景音视频技术是近年…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
